9. Multiple Integrals in Curvilinear Coordinates

Exercises

    a. Integrating in Polar Coordinates

  1. Compute the integral \(\displaystyle \int_0^{\pi/2}\int_0^4 r\cos\theta\,dr\,d\theta\)

    Factor the integral.

    \(\displaystyle \int_0^{\pi/2}\int_0^4 r\cos\theta\,dr\,d\theta=8 \)

    We factor the integral: \[\begin{aligned} \int_0^{\pi/2}\int_0^4 r\cos\theta\,dr\,d\theta &=\int_0^{\pi/2}\cos\theta\,d\theta\int_0^4 r\,dr \\ &=\left[\rule{0pt}{10pt}\sin\theta\right]_0^{\pi/2}\left[\dfrac{1}{2}r^2\right]_0^{4}\\ &=1\left[8-0\right] =8 \end{aligned}\]

    wll 

  2. Compute the integral \(\displaystyle \int_0^{\pi/2}\int_0^5 r\,dr\,d\theta\). What shape do the limits describe?

    The integral factors.

    \(\displaystyle \int_0^{\pi/2}\int_0^5 r\,dr\,d\theta=\dfrac{25}{4}\pi\)
    It's a quarter circle of radius \(5\).

    We factor the integral: \[\begin{aligned} \int_0^{\pi/2}\int_0^5 &r\,dr\,d\theta =\int_0^5 r\,dr \int_0^{\pi/2} 1\,d\theta \\ &=\left[\dfrac{1}{2}r^2\right]_0^5\left[\rule{0pt}{10pt}\theta\right]_0^{\pi/2} =\dfrac{25}{2}\dfrac{\pi}{2} =\dfrac{25}{4}\pi \end{aligned}\] The limits are \[ 0 \le \theta \le \pi/2 \quad \text{and} \quad 0 \le r \le 5 \] So this is a quarter circle of radius \(5\).

    dm 

    Since this is the integral \(\displaystyle \iint\,dA\) where \(dA=r\,dr\,d\theta\), the integral measures the area. This is a quarter circle of radius \(5\). So its area is \(A=\dfrac{1}{4} \pi(5)^2=\dfrac{25}{4} \pi\) which agrees with our answer.

  3. Compute the integral \(\displaystyle \int_{\pi}^{2\pi}\int_0^\theta 15r^2\theta\,dr\,d\theta\)

    The integral cannot be factored. So do the \(r\) integral and then the \(\theta\) integral.

    \(\displaystyle \int_{\pi}^{2\pi}\int_0^\theta r^2\theta\,dr\,d\theta=31\pi^5 \)

    We start with the \(r\) integral: \[\begin{aligned} \int_{\pi}^{2\pi}\int_0^{\theta} 15r^2\theta\,dr\,d\theta &=\int_{\pi}^{2\pi} \left[\rule{0pt}{10pt}5r^3\theta\right]_{r=0}^{\theta}\,d\theta =\int_{\pi}^{2\pi} 5{\theta}^4 \,d\theta \\ &=\left[\rule{0pt}{10pt}\theta^5\right]_{\pi}^{2\pi} =32\pi^5-\pi^5 =31\pi^5 \end{aligned}\]

    wll 

  4. Find the area inside the cardioid \(r=1+\cos\theta\) by integrating in polar coordinates.

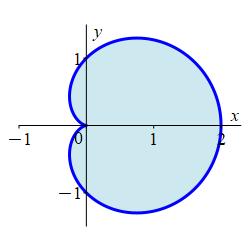
    The plot shows the area inside a cardioid with its large loop on the right and the 2 small bumps on the left.

    Don't forget the Jacobian \(r\). So set up the integral as: \[ \int_0^{2\pi}\int_0^{1+\cos\theta} r\,dr\,d\theta \]

    \(\displaystyle \int_0^{2\pi}\int_0^{1+\cos\theta} r\,dr\,d\theta=\dfrac{3}{2}\pi \)

    We compute the area as the integral: \[\begin{aligned} A&=\int_0^{2\pi}\int_0^{1+\cos\theta} r\,dr\,d\theta =\int_0^{2\pi}\left[\dfrac{r^2}{2}\right]_{r=0}^{1+\cos\theta}\,d\theta \\ &=\dfrac{1}{2}\int_0^{2\pi} (\cos\theta+1)^2\,d\theta =\dfrac{1}{2}\int_0^{2\pi}(\cos^2\theta+2\cos\theta+1) \,d\theta \\ &=\dfrac{1}{2}\int_0^{2\pi}\left(\dfrac{1+\cos(2\theta)}{2}+2\cos\theta+1\right) \,d\theta \\ &=\dfrac{1}{2}\left[\dfrac{1}{2}\left(\theta+\dfrac{\sin(2\theta)}{2}\right)+2\sin\theta+\theta\right]_0^{2\pi} =\dfrac{3}{2}\pi \end{aligned}\]

    dm,wll 

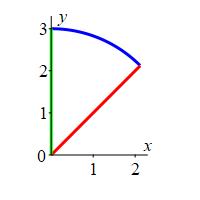
  5. Integrate the function \(\displaystyle f=\sqrt{x^2+y^2}\) over the region between \(y=x\), \(x=0\) and \(y=\sqrt{9-x^2}\)

    Plot the line (y=x\), the \(y\) axis and the circle \(x^2+y^2=9\). Describe the region inside in polar coordinates.

    The plot shows the region inside the piece of a circle between he angles theta = pi over 4 and pi over 2.

    \(\displaystyle \iint f(r,\theta)\,dA=\dfrac{9}{4}\pi\)

    We plot the line \(y=x\), the \(y\) axis and the circle \(x^2+y^2=9\). The region is shown at the right. In polar coordinates the region is: \[ \dfrac{\pi}{4} < \theta < \dfrac{\pi}{2} \quad \text{for} \quad 0 < r < 3 \] The integrand is \(f=\sqrt{x^2+y^2}=r\) and the area differential is \(dA=r\,dr\,d\theta\). We set up the integral and factor it: \[\begin{aligned} \iint r\,dA &=\int_{\pi/4}^{\pi/2}\int_0^3 r^2\,dr\,d\theta =\left[\rule{0pt}{10pt}\theta\right]_{\pi/4}^{\pi/2} \left[\dfrac{1}{3}r^3\right]_0^3 \\ &=\left(\dfrac{\pi}{2}-\dfrac{\pi}{4}\right)(9) =\dfrac{9}{4}\pi \end{aligned}\]

    The plot shows the piece of a circle between the angles theta = pi over 4 and pi over 2.

    dm.wll 

  6. Find the area of the circle \(r=\cos\theta\) by integrating in the polar coordinate system.

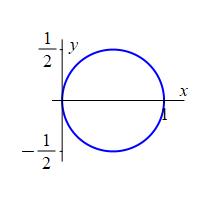
    The plot shows a circle of radius one half and center at x = one half on the x axis.

    When you plot the curve the circle lies only in quadrants I and IV. So you don't integrate from \(0\) to \(2\pi\).

    \( A=\dfrac{\pi}{4} \)

    The \(\theta\) limits are \(-\,\dfrac{\pi}{2} \le \theta \le \dfrac{\pi}{2}\) because the circle is only in quadrants I and IV. The area is: \[\begin{aligned} A&=\int_{-\pi/2}^{\pi/2}\int_0^{\cos\theta} r\,dr\,d\theta =\int_{-\pi/2}^{\pi/2}\left[\dfrac{r^2}{2}\right]_0^{\cos\theta}\,d\theta \\ &=\int_{-\pi/2}^{\pi/2} \dfrac{1}{2}\cos^2\theta\,d\theta =\dfrac{1}{4}\int_{-\pi/2}^{\pi/2} 1+\cos(2\theta)\,d\theta \\ &=\dfrac{1}{4}\left[\theta+\dfrac{\sin(2\theta)}{2}\right]_{-\pi/2}^{\pi/2} =\dfrac{\pi}{4} \end{aligned}\]

    dm,wll 

  7. Find the area outside of the circle \(r=1\) and inside the cardioid \(r=2-2\cos\theta\). The curves are plotted with the region of interest in blue.

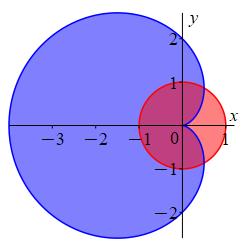
    The plot shows a cardioid with its large loop on the left and the 2 small bumps on the right. It also has a circle of radius 1 centered at the origin. The region inside the cardioid but outside the circle is colored blue.

    In this problem the bounds of integration go from \(r=1\) to \(r=2-2\cos\theta\) (because the circle is the minimum value of \(r\) and the cardioid is the maximum value of \(r\)) while the bounds of \(\theta\) must be calculated from the intersection of the circle and the cardioid.

    \(\displaystyle A=\int_{\pi/3}^{5\pi/3}\int_1^{2-2\cos\theta} r\,dr\,d\theta =\dfrac{10}{3}\pi+\dfrac{7}{2}\sqrt{3} \)

    In polar coordinates, \(r\) ranges from \(1\) to \(2-2\cos\theta\). The \(\theta\) bounds must be calculated from the intersection of the circle and the cardioid. We do this by setting \[ r=1=2-2\cos\theta \] So \[ 2\cos\theta=1 \qquad \text{or} \qquad \cos\theta=\dfrac{1}{2} \qquad \text{or} \qquad \theta=\dfrac{\pi}{3}, \dfrac{5\pi}{3} \] (Note: We use \(\dfrac{5\pi}{3}\) instead of \(-\,\dfrac{\pi}{3}\) because the latter would give an integral across the positive \(x\)-axis instead of the negative \(x\)-axis.) Now that we have the limits we can set up the area integral: \[\begin{aligned} A&=\int_{\pi/3}^{5\pi/3}\int_1^{2-2\cos\theta} r\,dr\,d\theta \\ &=\int_{\pi/3}^{5\pi/3}\left[\dfrac{r^2}{2}\right]_1^{2-2\cos\theta}\,d\theta \\ &=\dfrac{1}{2}\int_{\pi/3}^{5\pi/3} [(2-2\cos\theta)^2-1^2]\,d\theta \\ &=\dfrac{1}{2}\int_{\pi/3}^{5\pi/3} (4\cos^2\theta-8\cos\theta+3)\,d\theta \\ &=\dfrac{1}{2}\int_{\pi/3}^{5\pi/3} (2[1+\cos(2\theta)]-8\cos\theta+3)\,d\theta \\ &=\dfrac{1}{2}\left[\rule{0pt}{10pt}5\theta+\sin(2\theta)-8\sin\theta\right]_{\pi/3}^{5\pi/3} \\ &=\dfrac{1}{2}\left(\dfrac{25\pi}{3}+\sin\dfrac{10\pi}{3}-8\sin\dfrac{5\pi}{3}\right) \\ &\quad-\dfrac{1}{2}\left(\dfrac{5\pi}{3}+\sin\dfrac{2\pi}{3}-8\sin\dfrac{\pi}{3}\right) \\ &=\dfrac{1}{2}\left(\dfrac{25\pi}{3}-\dfrac{\sqrt{3}}{2}+4\sqrt{3}\right) \\ &\quad-\dfrac{1}{2}\left(\dfrac{5\pi}{3}+\dfrac{\sqrt{3}}{2}-4\sqrt{3}\right) \\ &=\dfrac{10}{3}\pi+\dfrac{7}{2}\sqrt{3} \end{aligned}\]

    dm,wll 

    8. b. Integrating in Cylindrical Coordinates

  8. Compute the integral \(\displaystyle \int_2^4\int_0^\pi\int_0^1 r\,dr\,d\theta\,dz\)

    Since the limits are all constants and the integrand factors, the integral separates.

    \(\displaystyle\int_2^4\int_0^\pi\int_0^1 r\,dr\,d\theta\,dz=\pi\)

    The integral separates: \[\begin{aligned} \int_2^4\int_0^\pi\int_0^1 r\,dr\,d\theta\,dz &=\int_2^4 \,dz\int_0^\pi \,d\theta\int_0^1 r\,dr \\ &=2\pi\left[\dfrac{r^2}{2}\right]_0^1 =\pi \end{aligned}\]

    dm,wll 

  9. Compute the integral \(\displaystyle \iiint x^2\,dV\) over the cylinder with diameter \(4\) and height between \(z=0\) and \(z=3\).

    Convert \(x^2\) to cylindrical coordinates using: \[ x=r\cos\theta \] The diameter is 4. What is the radius? It's needed for the \(r\) integral The integral goes all around the cylinder. Therefore the \(\theta\) bounds are \(0\) to \(2\pi\). Remember \(dV=r\,dr\,dz\,d\theta\).

    \(\displaystyle \int_0^3\int_0^{2\pi}\int_0^2 r^3\cos^2\theta\,dr\,d\theta\,dz=12\pi \)

    The integral can be set up as: \[\begin{aligned} \iiint x^2\,dV &=\iiint r^2\cos^2\theta\,dV \\ &=\int_0^3\int_0^{2\pi}\int_0^2 r^2\cos^2\theta\,r\,dr\,d\theta\,dz \end{aligned}\] The integral factors as: \[\begin{aligned} \iiint x^2\,dV &=\int_0^3 \,dz\int_0^{2\pi} \cos^2\theta\,d\theta\int_0^2 r^3\,dr \\ &=3\int_0^{2\pi} \dfrac{1+\cos(2\theta) }{2}\,d\theta \dfrac{1}{4}\left[r^4\dfrac{}{}\right]_0^2 \\ &=12\left[\dfrac{1}{2}\left(\theta+\dfrac{\sin(2\theta) }{2}\right)\right]_0^{2\pi} \\ &=12\pi \end{aligned}\]

    dm,wll 

  10. Compute the integral \(\displaystyle \iiint (x^2+y^2)\,dV\) over the cylindrical region with the base in the \(xy\) plane centered at the origin having a diameter of \(8\) and a height of \(2\).

    You will need to change the function \(x^2+y^2\) into polar form in order to compute the integral in polar coordinates. What is the radius?

    \(\displaystyle \int_0^2\int_0^{2\pi}\int_0^4 r^2\,r\,dr\,d\theta\,dz=256\pi \)

    The diameter is \(8\), so the radius is \(4\). The integral can be computed as \[\begin{aligned} \int_0^2\int_0^{2\pi}\int_0^4 r^2\,r\,dr\,d\theta\,dz &=\int_0^2 \,dz\int_0^{2\pi} \,d\theta\int_0^4 r^3\,dr \\ &=2\cdot2\pi\left[\dfrac{1}{4}r^4\right]_0^4 =256\pi \end{aligned}\]

    dm,wll 

  11. The solid at the right was made by revolving the curve \(x=4-z^2\) with \(y=0\) (shown in black) around the \(z\)-axis. So in cylindrical coordinates, the surface is \(r=4-z^2\) independent of \(\theta\).

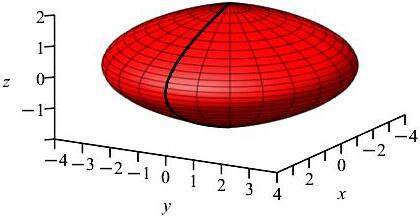
    The plot shows a solid formed by rotating a sidewise parabola around ait base. It looks like an M&M with a point at the top and bottom.

    1. Find the volume.

      \(V=\dfrac{512}{15}\pi\)

      Since \(r=4-z^2\) is a function of \(z\), we put the \(r\)-integral inside. The volume is: \[\begin{aligned} V&=\iiint 1\,dV =\int_0^{2\pi}\int_{-2}^2\int_0^{4-z^2} r\,dr\,dz\,d\theta \\ &=2\pi\int_{-2}^2 \left[\dfrac{r^2}{2}\right]_0^{4-z^2}\,dz =\pi\int_{-2}^2 (4-z^2)^2\,dz \\ &=\pi\int_{-2}^2 (16-8z^2+z^4)\,dz =\pi\left[16z-8\,\dfrac{z^3}{3}+\dfrac{z^5}{5}\right]_{-2}^2 \\ &=2\pi\left(32-\,\dfrac{64}{3}+\dfrac{32}{5}\right) =64\pi\left(1-\,\dfrac{2}{3}+\dfrac{1}{5}\right) =\dfrac{512}{15}\pi \end{aligned}\]

      This shape is contained in a cylinder of radius \(r=4\) and height \(h=4\) whose volume is \(V=\pi r^2h=64\pi\). So having a volume \(V=\dfrac{512}{15}\pi\approx32.1\pi\) is reasonable.

    2. Find the mass if the density is \(\delta=r\).

      \(M=\dfrac{8192}{105}\pi\)

      Since the density is \(\delta=r\) the mass is: \[\begin{aligned} M&=\iiint \delta\,dV =\int_0^{2\pi}\int_{-2}^2\int_0^{4-z^2} r^2\,dr\,dz\,d\theta \\ &=2\pi\int_{-2}^2 \left[\dfrac{r^3}{3}\right]_0^{4-z^2}\,dz =\dfrac{2}{3}\pi\int_{-2}^2 (4-z^2)^3\,dz \\ &=\dfrac{2}{3}\pi\int_{-2}^2 (64-48z^2+12z^4-z^6)\,dz \\ &=\dfrac{2}{3}\pi\left[64z-16z^3+12\dfrac{z^5}{5}-\,\dfrac{z^7}{7}\right]_{-2}^2 \\ &=\dfrac{4}{3}\pi\left(128-128+12\dfrac{32}{5}-\,\dfrac{128}{7}\right) \\ &=\dfrac{512}{3}\pi\left(1-1+\dfrac{3}{5}-\,\dfrac{1}{7}\right) =\dfrac{8192}{105}\pi \end{aligned}\]

    3. Find the average density if the density is \(\delta=r\).

      \(\delta_\text{ave}=\dfrac{16}{7}\)

      The average density is: \[ \delta_\text{ave}=\dfrac{1}{V}\iiint \delta\,dV \] We already computed the volume is \(V=\dfrac{512}{15}\pi\). The numerator is just the mass \(M=\dfrac{8192}{105}\pi\). So the average \[ \delta_\text{ave}=\dfrac{M}{V} =\dfrac{8192\pi}{105}\dfrac{15}{512\pi} =\dfrac{16}{7} \]

      The largest the radius can be is \(r=4\). So the largest the density can be is \(\delta=4\). So having an average density of \(\delta_\text{ave}=\dfrac{16}{7}\approx2.3\) is reasonable.

  12. Find the centroid of the the region beneath the cone \(z=4-r\) and above the \(xy\) plane.

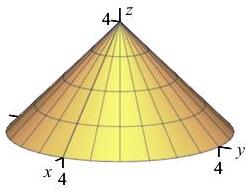
    The plot shows a cone with radius 4 and height 4.

    Recognize that since the object is symmetrical about the \(z\) axis, the coordinates of the centroid will take the form of \((0,0,\bar z)\).

    \(\left\langle \bar{x},\bar{y},\bar{z}\right\rangle =\left\langle 0,0,1\right\rangle\)

    The \(x\) and \(y\) components of the centroid are both zero due to the symmetry of the object about the \(z\) axis, as you can easily see in the plot. The \(z\) component of the centroid of the cone, however must be computed. The formula for \(\bar{z}\) is: \[ \bar{z}=\dfrac{1}{V}\iiint_R z\,r\,dr\,d\theta\,dz \] You should remember the formula for the volume of a cone is \[\begin{aligned} V&=\dfrac{1}{3}\pi r^2h \\ &=\dfrac{1}{3}\pi(4)^2(4)=\dfrac{64}{3}\pi \end{aligned}\] However it is useful to recompute it to identify the correct structure of the integral: \[\begin{aligned} V&=\iiint_R r\,dr\,d\theta\,dz =\int_0^{2\pi}\int_0^4\int_0^{4-r} r\,dz\,dr\,d\theta \\ &=\int_0^{2\pi}\,d\theta\int_0^4 \left[zr\dfrac{}{}\right]_{z=0}^{4-r}\,\,dr =2\pi\int_0^4 (4-r)r\,dr \\ &=2\pi\left[2r^2-\,\dfrac{r^3}{3}\right]_0^4 \\ &=\dfrac{64}{3}\pi \end{aligned}\] Next we compute the \(z\)-moment of the volume as \[\begin{aligned} V_z&=\iiint_R z\,r\,dr\,d\theta\,dz =\int_0^{2\pi}\int_0^4\int_0^{4-r} z\,r\,dz\,dr\,d\theta \\ &=\int_0^{2\pi}d\theta\int_0^4 \left[\dfrac{z^2}{2}r\right]_{z=0}^{4-r}\,\,dr =2\pi\dfrac{1}{2}\int_0^4 (4-r)^2r\,dr \\ &=\pi\int_0^4 (16r-8r^2+r^3)\,dr =\pi\left[8r^2-\,\dfrac{8}{3}r^3+\dfrac{1}{4}r^4\right]_0^4 \\ &=\pi\left(8(4)^2-\,\dfrac{8}{3}(4)^3+\dfrac{1}{4}(4)^4\right) =\dfrac{64}{3}\pi \end{aligned}\] Thus the \(z\)-component of the centroid is \[ \bar{z}=\dfrac{V_z}{V}=\dfrac{64\pi}{3}\dfrac{3}{64\pi}=1 \] and so the centroid is \[ \left\langle \bar{x},\bar{y},\bar{z}\right\rangle =\left\langle 0,0,1\right\rangle \]

    Notice that \(\bar{z}=1=\dfrac{h}{4}\). This result can be generalized for the centroid of any cone with its base on the \(xy\) plane with a height \(h\): \[ \left\langle \bar{x},\bar{y},\bar{z}\right\rangle =\left\langle 0,0,\dfrac{1}{4}h\right\rangle \] Try to prove it.

  13. Challenge Problem: Find the 4-Volume below the function \(w=zr^2\) and above the \(w=0\) hyperplane within the region between the cone \(z=4-r\) and the \(xy\) plane.

    The plot shows a cone with radius 4 and height 4.

    \(V_4=\dfrac{1024}{15}\pi\)

    The \(4\)-Volume is the triple integral: \[\begin{aligned} V_4&=\iiint zr^2\,dV =\int_0^{2\pi}\int_0^4\int_0^{4-r} zr^2\,r\,dz\,dr\,d\theta \\ &=\int_0^{2\pi} \,d\theta\int_0^4 \left[\dfrac{z^2}{2}r^3\right]_{z=0}^{4-r}\,dr =\dfrac{2\pi}{2}\int_0^4 (4-r)^2r^3\,dr \\ &=\pi\int_0^4 r^5-8r^4+16r^3\,dr =\pi\left[\dfrac{1}{6}r^6-\,\dfrac{8}{5}r^5+4r^4\right]_0^4 \\ &=\pi\left(\dfrac{1}{6}(4)^6-\,\dfrac{8}{5}(4)^5+4(4)^4\right) =\dfrac{1024}{15}\pi \end{aligned}\]

    14. c. Integrating in Spherical Coordinates

  14. Compute the integral \(\displaystyle \int_0^\pi\int_0^{2\pi}\int_0^5 \rho\,d\rho\,d\theta\,d\phi\)

    \(\displaystyle \int_0^\pi\int_0^{2\pi}\int_0^5 \rho\,d\rho\,d\theta\,d\phi =25\pi^2 \)

    \[\begin{aligned} \int_0^\pi\int_0^{2\pi}\int_0^5 \rho\,d\rho\,d\theta\,d\phi &=\int_0^\pi \,d\phi\int_0^{2\pi} \,d\theta\int_0^5 \rho\,d\rho\\ &=\pi\cdot2\pi\left[\dfrac{\rho^2}{2}\right]_0^5 \\ &=25\pi^2 \end{aligned}\]

    dm 

  15. Compute the integral \(\displaystyle \int_0^\pi\int_0^{\sin\phi}\int_0^1 \rho\,d\rho\,d\theta\,d\phi\)

    \(\displaystyle \int_0^\pi\int_0^{\sin\phi}\int_0^1 \rho\,d\rho\,d\theta\,d\phi=1\)

    \[\begin{aligned} \int_0^\pi\int_0^{\sin\phi}\int_0^1 &\rho\,d\rho\,d\theta\,d\phi =\int_0^\pi\int_0^{\sin\phi} \dfrac{1}{2}\left[\rho^2\dfrac{}{}\right]_0^1\,d\theta\,d\phi \\ &=\dfrac{1}{2}\int_0^\pi\int_0^{\sin\phi} 1\,d\theta\,d\phi =\dfrac{1}{2}\int_0^\pi \sin\phi\,d\phi \\ &=\dfrac{1}{2}\left[\rule{0pt}{10pt}-\cos\phi\right]_0^\pi =\dfrac{1}{2}(2) =1 \end{aligned}\]

    dm 

  16. Compute the integral \(\displaystyle \int_0^\pi\int_0^\pi\int_0^1 \rho\,d\rho\,d\theta\,d\phi\). In spherical coordinates, what shape do the limits describe?

    \(\displaystyle \int_0^\pi\int_0^\pi\int_0^1 \rho\,d\rho\,d\theta\,d\phi\) factors.

    \(\displaystyle \int_0^\pi\int_0^\pi\int_0^1 \rho\,d\rho\,d\theta\,d\phi =\dfrac{1}{2}\pi^2\)

    The limits define the right half of a sphere. However, the integrand does not give the volume because the Jacobian is wrong!

    The plot shows the right half of a sphere.

    The integral factors: \[\begin{aligned} \int_0^\pi\int_0^\pi\int_0^1 &\rho\,d\rho\,d\theta\,d\phi =\int_0^\pi \,d\phi\int_0^\pi \,d\theta\int_0^1 \rho\,d\rho\\ &=\pi\cdot\pi\left[\dfrac{1}{2}\rho^2\right]_0^1 =\dfrac{1}{2}\pi^2 \end{aligned}\] The limits say \(\phi\) goes from the north pole to the south pole, \(\theta\) goes half way around the equator starting from the \(x\)-axis and \(\rho\) runs from the origin to a radius of \(1\). So the limits define the right half of a solid sphere. However, the integrand does not give the volume because the Jacobian is wrong!

    The plot shows the right half of a sphere.

    dm,tj 

  17. Compute the integral \(\displaystyle \iiint\,dV\) where \(0<\phi<\pi\) and \(0<\theta <2\pi\) and \(0<\rho<5\).

    \[ dV=\rho^2\sin\phi\,d\rho\,d\theta\,d\phi \] How can you check your answer?.

    \(\displaystyle \int_0^\pi\int_0^{2\pi}\int_0^5 \rho^2\sin\phi\,d\rho\,d\theta\,d\phi =\dfrac{500}{3}\pi\)

    For spherical coordinates, the volume diffferential is: \[ dV=\rho^2\sin\phi\,d\rho\,d\theta\,d\phi \] We set up and separate the integral as \[\begin{aligned} V&=\int_0^\pi\int_0^{2\pi}\int_0^5 \rho^2\sin\phi\,d\rho\,d\theta\,d\phi =\int_0^{2\pi} \,d\theta \int_0^\pi \sin\phi\,d\phi \int_0^5 \rho^2\,d\rho\\ &=2\pi \left[-\cos\phi\dfrac{}{}\right]_0^\pi \left[\dfrac{1}{3}\rho^3\sin\phi\right]_{\rho=0}^{\rho=5} =2\pi(2)\dfrac{125}{3} =\dfrac{500}{3}\pi \end{aligned}\]

    dm 

    You can check your answer by observing that this is simply a sphere, with volume: \[ V=\dfrac{4}{3}\pi r^3=\dfrac{4}{3}\pi 5^3=\dfrac{500}{3}\pi \]

  18. Compute the integral \(\displaystyle \iiint\dfrac{1}{z}\,dV\) over the ice cream cone given by \(0 \le \rho \le 5\) and \(0 \le \phi \le \dfrac{\pi}{4}\).

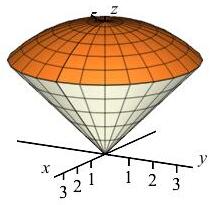
    The plot shows an ice cream cone. The sides are at 45 degrees and the top is a piece of a sphere.

    What is \(z\) in spherical coordinates?

    \(\displaystyle \iiint\dfrac{1}{z}\,dV=\dfrac{25\pi}{2}\ln2 \)

    In spherical coordinates, we know \(z=\rho\cos\phi\) and the volume element is: \[ dV=\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \] So we set up and compute the integral as: \[\begin{aligned} \iiint\dfrac{1}{z}\,dV &=\int_0^{2\pi}\int_0^{\pi/4}\int_0^5 \dfrac{\rho^2\sin\phi}{\rho\cos\phi}\,d\rho\,d\phi\,d\theta \\ &=\int_0^{2\pi} 1\,d\theta\int_0^{\pi/4} \dfrac{\sin\phi}{\cos\phi}\,d\phi\int_0^5 \rho\,d\rho \\ &=2\pi\left[-\ln(\cos x)\dfrac{}{}\right]_0^{\pi/4}\left[\dfrac{\rho^2}{2}\right]_0^5 \\ &=2\pi\left(-\ln\dfrac{1}{\sqrt{2}}+\ln1\right)\dfrac{25}{2} \\ &=25\pi\left(\dfrac{1}{2}\ln2\right) =\dfrac{25\pi}{2}\ln2 \end{aligned}\]

    dm 

  19. Find the mass of an apple given in spherical coordinates by \(\rho =1-\cos\phi\) if the mass density is \(\delta=\rho\) gm/cm\(^3\).

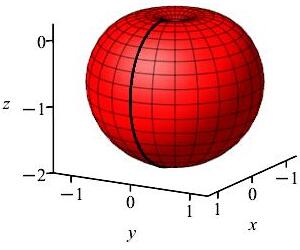
    The plot shows an apple with its stem dimple at the top.

    The volume of the apple is the region \(0 \le \rho \le 1-\cos\phi\) for \(0 \le \phi \le \pi\).

    \(\displaystyle M=\int_0^{2\pi}\int_0^\pi\int_0^{1-\cos\phi} \rho\cdot\rho^2\sin\phi\,d\rho\,d\phi\,d\theta=\dfrac{16}{5}\pi \)

    The mass can be found by integrating the density over the volume. In spherical coordinates, this is: \[\begin{aligned} M&=\int\int\int \delta\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\int_0^{2\pi}\int_0^\pi\int_0^{1-\cos\phi} \rho^3\sin\phi\,d\rho\,d\phi\,d\theta \\ &=2\pi\int_0^\pi\left[\dfrac{1}{4}\rho^4\right]_0^{1-\cos\phi} \sin\phi\,d\phi\\ &=2\pi\int_0^\pi \dfrac{1}{4}(1-\cos\phi)^4\sin\phi\,d\phi \end{aligned}\] Make the subsitution \(u=1-\cos\phi\) with \(du=\sin\phi\,d\phi\): \[ M=\dfrac{\pi}{2}\int_0^2u^4\,du =\dfrac{\pi}{2}\left.\dfrac{u^5}{5}\right|_0^2=\dfrac{16}{5}\pi \]

    wll 

    20. d. Integrating in 2D Curvilinear Coordinates

  20. Compute \(\displaystyle I=\int\int_R y^2\,dx\,dy\) where \(R\) is defined as the region bounded by \(y=\dfrac{1}{x},y=\dfrac{4}{x},y=x,\) and \(y=9x\).

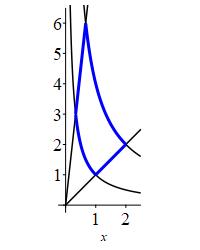
    The plot shows a diamond shaped region between 2 radial lines and 2 hyperbolas.

    Use a curvilinear coordinate system by defining \(u=xy\) and \(v=\dfrac{y}{x}\). Solve for \(x\) and \(y\) in terms of \(u\) and \(v\).

    \(\displaystyle I=30 \)

    We first need to define a coordinate system using \(u\) and \(v\). Rearranging the first two boundaries, we find \[ xy=1 \qquad \text{and} \qquad xy=4 \] We can use \(u=xy\) where \(u\) ranges from \(1\) to \(4\). The last two boundaries can be rearranged to \[ \dfrac{y}{x}=1 \qquad \text{and} \qquad \dfrac{y}{x}=9 \] So we let \(v=\dfrac{y}{x}\) where \(v\) ranges from \(1\) to \(9\). We solve for \(u,v\) in terms of \(x,y\) by multiplying and dividing the \(2\) equations: \[\begin{aligned} u=xy \quad &\text{and} \quad v=\dfrac{y}{x} \\ \implies uv=y^2 \quad &\text{and} \quad \frac{u}{v}=x^2 \end{aligned}\] So \[ x=\sqrt{\dfrac{u}{v}}=u^{1/2}v^{-1/2} \quad \text{and} \quad y=\sqrt{uv}=u^{1/2}v^{1/2} \] We compute the Jacobian: \[ \vec{e}_u =\left\langle \dfrac{\partial x}{\partial u},\dfrac{\partial y}{\partial u}\right\rangle =\left\langle \dfrac{1}{2}u^{-1/2}v^{-1/2},\dfrac{1}{2}u^{-1/2}v^{1/2}\right\rangle \] \[ \vec{e}_v =\left\langle \dfrac{\partial x}{\partial v},\dfrac{\partial y}{\partial v}\right\rangle =\left\langle -\,\dfrac{1}{2}u^{1/2}v^{-3/2},\dfrac{1}{2}u^{1/2}v^{-1/2}\right\rangle \] \[ J=\left|\dfrac{\partial (x,y) }{\partial (u,v) }\right| =\dfrac{1}{4v}+\dfrac{1}{4v}=\dfrac{1}{2v} \] Finally, we compute the integral \[\begin{aligned} I&=\iint_R y^2\,dx\,dy =\int_1^4\int_1^9 y(u,v)^2J\,dv\,du \\ &=\int_1^4\int_1^9 uv\dfrac{1}{2v}\,dv\,du=\dfrac{1}{2} \int_1^4\int_1^9 u\,dv\,du \\ &=\dfrac{1}{2}\left[\dfrac{u^2}{2}\right]_1^4\left[\rule{0pt}{10pt}v\right]_1^9 =\dfrac{1}{2}\left(\dfrac{16-1}{2}\right)(8) =30 \end{aligned}\]

    dm,tj 

  21. Compute the area of the ellipse \(4x^2+16y^2=36\)

    Use the substitutions \(x=3t\cos\phi\) and \(y=\dfrac{3}{2}t\sin\phi\). Check your solution with the formula for area of an ellipse: \(A=\pi ab\) where \(a,b\) are the major and minor radii.

    \(\displaystyle A=\dfrac{9}{2}\pi \)

    In standard form, the ellipse is: \[ \dfrac{x^2}{9}+\dfrac{4y^2}{9}=1 \] If we use the substitution \(x=3t\cos\phi\) and \(y=\dfrac{3}{2}t\sin\phi\), this equation becomes: \[ \dfrac{9t^2\cos^2\phi}{9}+\dfrac{9t^2\sin^2\phi}{9}=1 \quad \text{or} \quad t^2=1 \] So the bounds are \(0 \le t \le 1\) and \(0 \le \phi \le 2\pi\). We find the Jacobian: \[ \vec{e}_t=\left(3\cos\phi,\dfrac{3}{2}\sin\phi\right) \] \[ \vec{e}_\phi=\left(-3t\sin\phi,\dfrac{3}{2}t\cos\phi\right) \] \[ J=\dfrac{\partial (x,y) }{\partial (t,\phi) } =\left(\dfrac{9}{2}t\cos^2\phi+\dfrac{9}{2}t\sin^2\phi\right) =\dfrac{9}{2}t \] Finally, we can compute the integral: \[\begin{aligned} A&=\iint 1\cdot J\,dt\,d\phi =\int_0^{2\pi}\int_0^1 \dfrac{9}{2}t\,dt\,d\phi \\ &=2\pi\dfrac{9}{4}\left[\rule{0pt}{10pt}t^2\right]_0^1 =\dfrac{9}{2}\pi \end{aligned}\]

    dm 

    We can check our answer using the formula for area of an ellipse: \(A=\pi ab\) where \(a,b\) are the major and minor radii. Here \(a=3\) and \(b=\dfrac{3}{2}\). So \(A=\pi(3)\left(\dfrac{3}{2}\right)=\dfrac{9}{2}\pi\).

    Alternatively, the substitutions \(x=4u\) and \(y=2v\) could be used, followed by a change to polar coordinates. The answer will be the same.

    22. Compute the Jacobian factor for each of the following 2D coordinate systems:

  22. Here are the transformation equations and a plot of the coordinate curves. \[ x=uv \qquad y=\dfrac{1}{2}(v^2-u^2) \]

    Parabolic Coordinates
    This is the parabolic coordinate system consisting of two sets of parabolas, one opening upward and one opening downward. The two sets are always perpendicular to each other.

    The expression for the Jacobian factor is: \[\begin{aligned} J&=\left|\dfrac{\partial (x,y)}{\partial (u,v)}\right| = \left|\begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\[6pt] \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix}\right| = \left|\dfrac{\partial x}{\partial u}\dfrac{\partial y}{\partial v} -\,\dfrac{\partial y}{\partial u}\dfrac{\partial x}{\partial v}\right| \end{aligned}\] Remember it is the absolute value of the determinant.

    \(\displaystyle J=v^2+u^2 \)

    The Jacobian determinant is: \[\begin{aligned} \dfrac{\partial (x,y)}{\partial (u,v)} &=\begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\[6pt] \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} =\begin{vmatrix} v & -u \\ u & v \end{vmatrix} \\ &=v^2-(-u^2)=v^2+u^2 \end{aligned}\] Since this is positive, the Jacobian factor is \[ J=v^2+u^2 \]

    dm,wll 

  23. (Optional due to hyperbolic functions.)
    Here are the transformation equations and a plot of the coordinate curves. \[ x=a\cosh u\cos v \qquad y=a\sinh u\sin v \]

    Elliptic Hyperbolic Coordinates
    This is the elliptic hyperbolic coordinate system consisting of concentric ellipses with their principal axis along the x axis and hyperbolas which are always perpendicular to the ellipses.

    \(\begin{aligned}\displaystyle J&=a^2\sinh^2u\cos^2v+a^2\cosh^2u\sin^2v \\ &=a^2(\sinh^2u+\sin^2v) \\ &=a^2(\cosh^2u-\cos^2v) \end{aligned}\)

    The Jacobian determinant is \[\begin{aligned} \dfrac{\partial (x,y)}{\partial (u,v)} &=\begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\[6pt] \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} \\ &=\begin{vmatrix} a\sinh u\cos v & a\cosh u\sin v \\ -a\cosh u\sin v & a\sinh u\cos v \end{vmatrix} \\ &=a^2\sinh^2u\cos^2v+a^2\cosh^2u\sin^2v \end{aligned}\] Since this is positive, the Jacobian factor is: \[ J=a^2\sinh^2u\cos^2v+a^2\cosh^2u\sin^2v \] This can be written in several alternate forms: \[\begin{aligned} J&=a^2\sinh^2u(1-\sin^2v)+a^2\cosh^2u\sin^2v \\ &=a^2\sinh^2u-a^2\sinh^2u\sin^2v+a^2\cosh^2u\sin^2v \\ &=a^2\sinh^2u+a^2(\cosh^2u-\sinh^2u)\sin^2v \\ &=a^2(\sinh^2u+\sin^2v) \\ &=a^2([\cosh^2u-1]+[1-\cos^2v]) \\ &=a^2(\cosh^2u-\cos^2v) \end{aligned}\]

    dm,wll 

    24. e. Integrating in 3D Curvilinear Coordinates

    Compute the Jacobian factor for each of the following 3D coordinate systems:xxx

  24. Here are the transformation equations and a plot of its coordinate surfaces: \[ x=\rho\sin\phi\cos\theta \qquad y=\rho\sin\phi\sin\theta \qquad z=\rho\cos\phi \] for \(\rho \ge 0\), \(0 \le \phi \le \pi\) and \(0 \le \theta \le 2\pi\).

    Spherical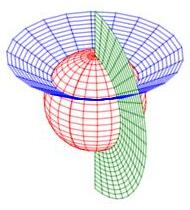
    The plot shows the spherical coordinates system. There is one surface for each coordinate. The rho-surface is a sphere. The phi-surface is cone with vertex at the origin. The theta-surface is a vertical half plane.

    Follow these steps:

    • Find the coordinate tangent vectors: \(\vec e_\rho\), \(\vec e_\phi\) and \(\vec e_\theta\).
    • The Jacobian determinant is their triple product: \[ \dfrac{\partial (x,y,z)}{\partial (\rho,\phi,\theta)} =\vec e_\rho\cdot\vec e_\phi\times\vec e_\theta \]
    • The Jacobian factor is the absolute value: \[ J=\left|\dfrac{\partial (x,y,z)}{\partial (\rho,\phi,\theta)}\right| \]

    \(\displaystyle J=\rho^2\sin\phi \)

    This one, you should do yourself, so you see all the miraculous cancellation.

    dm 

  25. Here are the transformation equations and a plot of its coordinate surfaces: \[ x=uv\cos\theta \qquad y=uv\sin\theta \qquad z=\dfrac{1}{2}(v^2-u^2) \] for \(u \ge 0\), \(v \ge 0\) and \(0 \le \theta \le 2\pi\).

    Paraboloidal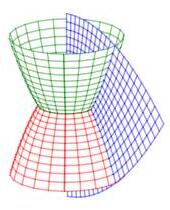
    The plot shows the paraboloidal coordinates system. There is one surface for each coordinate. The first surface is a paraboloid opening up. The second surface is a paraboloid opening down. The third surface is a vertical half plane.

    \(\displaystyle J=uv(u^2+v^2) \)

    The Jacobian determinant is: \[\begin{aligned} \dfrac{\partial (x,y,z)}{\partial (u,v,\theta)} &=\begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} & \dfrac{\partial z}{\partial u} \\[6pt] \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} & \dfrac{\partial z}{\partial v} \\[6pt] \dfrac{\partial x}{\partial \theta} & \dfrac{\partial y}{\partial \theta} & \dfrac{\partial z}{\partial \theta} \end{vmatrix} \\ &=\begin{vmatrix} v\cos\theta & v\sin\theta & -u\\ u\cos\theta & u\sin\theta & v\\ -uv\sin\theta & uv\cos\theta\ & 0 \end{vmatrix} \end{aligned}\] We expand on the third column: \[\begin{aligned} \dfrac{\partial (x,y,z)}{\partial (u,v,\theta)} &=-u(u^2v\cos^2\theta+u^2v\sin^2\theta) \\ &\quad-v(uv^2\cos^2\theta+uv^2\sin^2\theta) \\ &=-u^3v-uv^3 \\ &=-uv(u^2+v^2) \end{aligned}\] So the Jacobian factor is its absolute value: \[ J\left|\dfrac{\partial (x,y,z)}{\partial (u,v,\theta)}\right| =uv(u^2+v^2) \] since \(u\) and \(v\) are positive.

    dm,wll 

  26. Here are the transformation equations and a plot of its coordinate surfaces: \[ x=a\rho\sin\phi\cos\theta \qquad y=b\rho\sin\phi\sin\theta \qquad z=c\rho\cos\phi \] for \(\rho \ge 0\), \(0 \le \phi \le \pi\) and \(0 \le \theta \le 2\pi\). Assume \(a\), \(b\) and \(c\) are positive.

    Ellipsoidal Spherical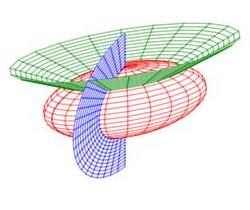
    The plot shows the ellipsoidal spherical coordinates system. There is one surface for each coordinate. The rho-surface is an ellipsoid. The phi-surface is cone with vertex at the origin. The theta-surface is a vertical half plane. It looks like a squished spherical coordinate system.

    \(\displaystyle J=abc\rho^2\sin\phi \)

    The Jacobian determinant is: \[\begin{aligned} \dfrac{\partial (x,y,z)}{\partial (\rho,\phi,\theta)} &=\begin{vmatrix} \dfrac{\partial x}{\partial \rho} & \dfrac{\partial y}{\partial \rho} & \dfrac{\partial z}{\partial \rho} \\[6pt] \dfrac{\partial x}{\partial \phi} & \dfrac{\partial y}{\partial \phi} & \dfrac{\partial z}{\partial \phi} \\[6pt] \dfrac{\partial x}{\partial \theta} & \dfrac{\partial y}{\partial \theta} & \dfrac{\partial z}{\partial \theta} \end{vmatrix} \\ &=\begin{vmatrix} a\sin\phi\cos\theta & b\sin\phi\sin\theta & c\cos\phi\\ a\rho\cos\phi\cos\theta & b\rho\cos\phi\sin\theta & -c\rho\sin\phi\\ -a\rho\sin\phi\sin\theta & b\rho\sin\phi\cos\theta & 0 \end{vmatrix} \end{aligned}\] We expand on the third column: \[\begin{aligned} \dfrac{\partial (x,y,z)}{\partial (\rho,\phi,\theta)} &=c\cos\phi(ab\rho^2\sin\phi\cos\phi\cos^2\theta + ab\rho^2\sin\phi\cos\phi\sin^2\theta)\\ &+c\rho\sin\phi(ab\rho\sin^2\phi\cos^2\theta + ab\rho\sin^2\phi\sin^2\theta) \\ &=abc\rho^2\cos^2\phi\sin\phi(\cos^2\theta + \sin^2\theta) \\ &+abc\rho^2\sin^3\phi(\cos^2\theta + \sin^2\theta)\\ &=abc\rho^2\cos^2\phi\sin\phi + abc\rho^2\sin^3\phi \\ &=abc\rho^2\sin\phi(\cos^2\phi+\sin^2\phi) \\ &=abc\rho^2\sin\phi \end{aligned}\] So the Jacobian factor is \[ J=\left|\dfrac{\partial (x,y,z)}{\partial (\rho,\phi,\theta)}\right| =abc\rho^2\sin\phi \] We don't need any absolute values since \(a\), \(b\) and \(c\) are positive and \(\sin\phi\) is positive for \(0 \le \phi \le \pi\).

    dm,wll 

    This is the same as spherical coordinates if we let \(a=b=c=1\).

  27. Compute the mass of the ellipsoid \(x^2+4y^2+9z^2=36\), discussed in an exercise on a previous page, but this time with the density \(\delta=\rho\) where \(\rho\) is the radial coordinate in ellipsoidal coordinates.

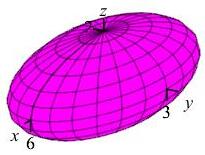
    The plot shows an ellipsoid which intersects the x axis at plus and minus 6, intersects the y axis at plus and minus 3 and intersects the z axis at plus and minus 2.

    \(M=36\pi\)

    We write the ellipsoid in standard form as \(\dfrac{x^2}{36}+\dfrac{y^2}{9}+\dfrac{z^2}{4}=1\) So we use ellipsoidal coordinates: \[\begin{aligned} x&=6\rho\sin\phi\cos\theta \\ y&=3\rho\sin\phi\sin\theta \\ z&=2\rho\cos\phi \end{aligned}\] whose Jacobian factor is \(J=36\rho^2\sin\phi\). The mass of the ellipsoid is found by integrating the density function over the volume \[\begin{aligned} M&=\iiint_R \delta\,dV =\iiint_R \rho36\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=72\pi\int_0^\pi \sin\phi\,d\phi\int_0^1 \rho^3\,d\rho =72\pi\left[-\cos\phi\dfrac{}{}\right]_0^\pi\left[\dfrac{1}{4}\rho^4\right]_0^1 \\ &=72\pi(1+1)\dfrac{1}{4}(1) =36\pi \end{aligned}\]

  28. Compute the volume integral \(\displaystyle V=\iiint\,dV\) over the sphere \(x^2+y^2+z^2=4\) using the Jacobian for spherical coordinates found above. Check your answer with the formula for volume of a sphere.

    The formula for the volume of an object in spherical coordinates is \[\begin{aligned} V&=\int\int\int dV=\int\int\int J\,d\rho\,d\phi\,d\theta \end{aligned}\]

    \(\displaystyle \iiint dV=\dfrac{32\pi}{3} \)

    We use spherical coordinates: \[\begin{aligned} x=\rho\sin\phi\cos\theta \qquad y=\rho\sin\phi\sin\theta \qquad z=\rho\cos\phi \end{aligned}\] From the previous problem, the Jacobian is: \[ J=\rho^2\sin\phi \] We can compute the volume as \[\begin{aligned} V&=\int\int\int dV=\int\int\int J\,d\rho\,d\phi\,d\theta =\int_0^{2\pi}\int_0^\pi\int_0^2 \rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\left[\dfrac{\rho^3}{3}\right]_0^2 (2\pi)\left[-\cos\phi\dfrac{}{}\right]_0^\pi =\dfrac{16}{3}\pi\left[-(-1)-(-1)\right] =\dfrac{32}{3}\pi \end{aligned}\] Checking this with the formula \(V=\dfrac{4}{3}\pi r^3\): \[ V=\dfrac{4}{3}\pi(2)^3=\dfrac{32}{3}\pi \]

    dm 

    29. Review Exercises

  29. Compute \(\displaystyle \iiint (x^2+y^2+4z)dV\) over the colosseum-shaped region below the surface \(z=\dfrac{x^2+y^2}{8}\) and above the surface \(z=\dfrac{1}{2}\) above the ring between the circles with radii \(r=2\) and \(r=4\).

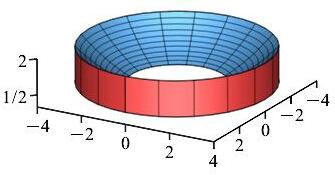
    The plot looks like a colosseum. It has a flat bottom at height z = one half in the shape of ring between radii r = 2 and r = 4. The outside is a cylinder at radius r = 4, between z = one half and z = 2. The inside is a slanted surface from the ring at r = 2 to the top of the cylinder at r = 4.

    Use cylindrical coordinates to compute the integral.

    \(\displaystyle \iiint (x^2+y^2+4z)dV =\int_0^{2\pi}\int_2^4\int_{1/2}^{r^2/8} (r^2+4z)r\,dz\,dr\,d\theta =144\pi \)

    In cylindrical coordinates, \(x^2+y^2=r^2\). So the integrand becomes \(r^2+4z\) and the \(z\)-bounds are \(\dfrac{1}{2} \lt z \lt \dfrac{r^2}{8}\). Also remember the Jacobian is \(r\,dz\,dr\,d\theta\). Thus, the integral becomes: \[\begin{aligned} &\int_0^{2\pi}\int_2^4\int_{1/2}^{r^2/8} (r^2+4z)r\,dz\,dr\,d\theta =2\pi\int_2^4 \left[\rule{0pt}{10pt}r^3z+2rz^2\right]_{z=1/2}^{r^2/8}\,dr \\ &\quad=2\pi\int_2^4 \left(\dfrac{r^5}{8}+\dfrac{r^5}{32}-\dfrac{r^3}{2}-\dfrac{r}{2}\right)\,dr \\ &\quad=\dfrac{2\pi}{32}\int_2^4 (5r^5-16r^3-16r)\,dr =\dfrac{\pi}{16}\left[\dfrac{5r^6}{6}-4r^4-8r^2\right]_2^4 \\ &\quad=\dfrac{\pi}{16}\left(\dfrac{5\cdot4^6}{6}-4\cdot4^4-8\cdot4^2\right) -\dfrac{\pi}{16}\left(\dfrac{5\cdot2^6}{6}-4\cdot2^4-8\cdot2^2\right) \\ &\quad=\pi\left(\dfrac{5\cdot4^4}{6}-4^3-8\right) -\pi\left(\dfrac{5\cdot4}{6}-4-2\right) \\ &\quad=\pi\left(\dfrac{1280-384-48-20+24+12}{6}\right) =144\pi \end{aligned}\]

    dm,wll 

  30. Evaluate the integral \(\displaystyle \iint \exp\left(\dfrac{x-y}{x+y}\right)\,dx\,dy\) over the trapezoid with vertices \((4,0)\), \((5,0)\), \((0,5)\) and \((0,4)\). Use the coordinates: \[ u=x+y \qquad v=x-y \]

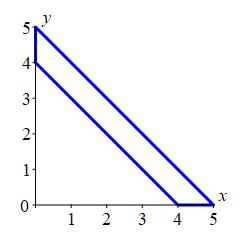
    The plot shows a trapezoid. The parallel edges have slope -1. The slanted edges are on the x and y axes.

    The bounds are \(y=4-x\), \(y=5-x\), \(x=0\) and \(y=0\). Express these in terms of \(u\) and \(v\). To find the Jacobian, you must first solve for \(x\) and \(y\).

    \(\displaystyle \iint \exp\left(\dfrac{x-y}{x+y}\right)\,dx\,dy =\dfrac{9}{4}\left(e-\dfrac{1}{e}\right)\)

    To find the Jacobian, we first solve for \(x\) and \(y\). By adding and subtracting the two equations we get: \[ u+v=2x \qquad u-v=2y \] So \[ x=\dfrac{u+v}{2} \qquad y=\dfrac{u-v}{2} \] So the Jacobian is \[ J=\left| \begin{vmatrix} \dfrac{1}{2} & \dfrac{1}{2} \\[8pt] \dfrac{1}{2} & -\,\dfrac{1}{2} \end{vmatrix} \right| =\left|-\,\dfrac{1}{4}-\dfrac{1}{4}\right|=\dfrac{1}{2} \] To find the limits on the integral, we look at the boundary of the region. The equations of the parallel lines are \[\begin{aligned} y=4-x \qquad &\text{and} \qquad y=5-x \\ &\quad\text{or} \\ u=x+y=4 \qquad &\text{and} \qquad u=x+y=5 \end{aligned}\] So the bounds for \(u\) are \(4 \le u \le 5\). We find the bounds for \(v\) by looking at the other \(2\) edges: \[\begin{aligned} x=0 \qquad &\text{says} \qquad \dfrac{u+v}{2}=0 \qquad \text{or} \qquad v=-u \\ y=0 \qquad &\text{says} \qquad \dfrac{u-v}{2}=0 \qquad \text{or} \qquad v=u \\ \end{aligned}\] So the bounds for \(v\) are \(-u \le v \le u\). We can now do the integral: \[\begin{aligned} \iint &\exp\left(\dfrac{x-y}{x+y}\right)\,dx\,dy =\int_4^5\int_{-u}^u \exp\left(\dfrac{v}{u}\right)\dfrac{1}{2}\,dv\,du \\ &=\dfrac{1}{2}\int_4^5 \left[u\,\exp\left(\dfrac{v}{u}\right)\right]_{v=-u}^u\,du =\dfrac{1}{2}\int_4^5 (ue^1-ue^{-1})\,du \\ &=\dfrac{1}{2}\left(e-\dfrac{1}{e}\right)\left[\dfrac{u^2}{2}\right]_4^5 =\dfrac{1}{2}\left(e-\dfrac{1}{e}\right)\left(\dfrac{25-16}{2}\right) \\ &=\dfrac{9}{4}\left(e-\dfrac{1}{e}\right) \end{aligned}\]

    dm,wll 

  31. Find the centroid of the quarter circle in the first quadrant of radius \(4\).

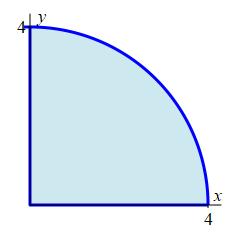
    The plot shows a quarter circle of radius 4 in the first quadrant.

    \(\displaystyle (\bar x, \bar y)=\left(\dfrac{16}{3\pi},\dfrac{16}{3\pi}\right) \)
    \(\displaystyle (\bar r, \bar \theta)=\left(\dfrac{16\sqrt{2}}{3\pi},\dfrac{\pi}{4}\right) \)

    The area of the region is one quarter of the area of a circle of radius \(4\): \[ A=\dfrac{1}{4}\pi(4)^2=4\pi \] However, to know how to compute the moments, it is useful to write down the integral which gives this result. The \(r\)-bounds are \(0\le r\le4\) and the \(\theta\)-bounds are \(0\le \theta \le \pi/2\). So the area is \[ A=\int_0^4\int_0^{\pi/2} r\,d\theta\,dr \] We next find the \(x\) and \(y\) moments of the area. Since \(x=r\cos\theta\), we have: \[\begin{aligned} A_x&=\int_0^4\int_0^{\pi/2} r^2\cos\theta\,d\theta\,dr\\ &=\int_0^{\pi/2}\cos\theta\,d\theta \int_0^4 r^2\,dr\\ &=\left[\rule{0pt}{10pt}\sin\theta\right]_0^{\pi/2}\left[\dfrac{r^3}{3}\right]_{0}^4 = \dfrac{64}{3} \end{aligned}\] Since \(y=r\sin\theta\), we have: \[\begin{aligned} A_y&=\int_0^4\int_0^{\pi/2} r^2\sin\theta\,d\theta\,dr\\ &=\int_0^{\pi/2}\sin\theta\,d\theta \int_0^4 r^2\,dr\\ &=\left[\rule{0pt}{10pt}-\cos\theta\right]_0^{\pi/2}\left[\dfrac{r^3}{3}\right]_{0}^4 = \dfrac{64}{3} \end{aligned}\] By symmetry, it is not surprizing they are equal. We can now find the centroid. First in rectangular coordinates: \[\begin{aligned} (\bar x, \bar y)&=\left(\dfrac{A_x}{A},\dfrac{A_y}{A}\right) =\left(\dfrac{64}{3}\dfrac{1}{4\pi},\dfrac{64}{3}\dfrac{1}{4\pi}\right) \\ &=\left(\dfrac{16}{3\pi},\dfrac{16}{3\pi}\right) \end{aligned}\] And now in polar coordinates: \[\begin{aligned} \bar r&=\sqrt{\bar x^2+\bar y^2}=\dfrac{16\sqrt{2}}{3\pi} \\ \bar \theta&=\arctan\dfrac{\bar y}{\bar x}=\arctan 1=\dfrac{\pi}{4} \end{aligned}\]

    wll 

  32. Find the volume inside the sphere \(x^2+y^2+z^2=25\) but outside the cylinder \(x^2+y^2=16\).

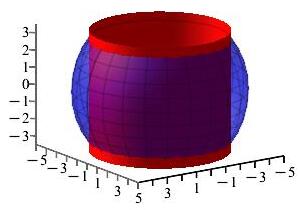
    The plot shows a sphere of radius 5 with a cylindrical hole cut out of radius 4.

    Use cylindrical coordinates.

    \(V=36\pi\)

    We will use cylindrical coordinates \(x=r\cos\theta, y=r\sin\theta, z=z\). The bounds are \(4\leq r \leq \sqrt{25-z^2}\) for \(-3\leq z\leq3\). So we set up a triple integral: \[\begin{aligned} V&=\iiint 1\,dV =\int_0^{2\pi}\int_{-3}^{3}\int_{4}^{\sqrt{25-z^2}}r\,drdzd\theta \\ &=2\pi\int_{-3}^{3}\int_{4}^{\sqrt{25-z^2}}r\,drdz =2\pi\int_{-3}^{3}\left[\dfrac{r^2}{2}\right]_{r=4}^{\sqrt{25-z^2}}\,dz\\ &=\pi\int_{-3}^{3}(25-z^2)-16\,dz\\ &=\pi\left[9z-\dfrac{z^3}{3}\right]_{-3}^{3} =2\pi(27-9) = 36\pi \end{aligned}\]

    gg 

  33. Find the mass of the planar region bounded by the parabolas \(x=4-y^2\) and \(x=-4+y^2\) for \(y \ge 0\), if the surface mass density is \(\delta=y\). For practice with curvilinear coordinates, use the coordinates: \[ u=x+y^2 \quad \text{and} \quad v=x-y^2 \]

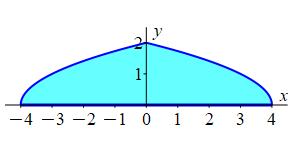
    The plot shows the region in the upper half plane between the parabolas y = 4 - x^2 and y = -4 + x^2.

    To compute the Jacobian, remember to solve \(u=x+y^2\) and \(v=x-y^2\) for \(x\) and \(y\).

    \(M=8\)

    We solve \(u=x+y^2\) and \(v=x-y^2\) to get: \[x=\dfrac{u+v}{2} \quad \text{and} \quad y=\dfrac{\sqrt{u-v}}{\sqrt{2}}\] We first find the Jacobian factor: \[\begin{aligned} J&=\left|\dfrac{\partial (x,y)}{\partial (u,v)}\right| = \left|\begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\[8pt] \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix}\right| = \left|\begin{vmatrix} \dfrac{1}{2} & \dfrac{1}{2\sqrt{2}\sqrt{u-v}}\\[8pt] \dfrac{1}{2} & \dfrac{-1}{2\sqrt{2}\sqrt{u-v}} \end{vmatrix}\right| \\ &=\left|\dfrac{-1}{4\sqrt{2}\sqrt{u-v}} - \dfrac{1}{4\sqrt{2}\sqrt{u-v}}\right| \\ &= \left|\dfrac{-1}{2\sqrt{2}\sqrt{u-v}}\right| = \dfrac{1}{2\sqrt{2}\sqrt{u-v}} \end{aligned}\]

    The bound \(x=4-y^2\) becomes \(u = 4\).
    The bound \(x=-4+y^2\) becomes \(v=-4\).
    And the bound \(y=0\) becomes \(v=u\).
    This is a triangle. So the mass is: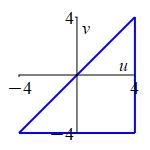

    The plot shows a triangle with vertices at (-4,-4), (4,-4) and (4,4).

    \[\begin{aligned} M&=\iint \delta\,dA=\iint y\,J\,du\,dv \\ &=\int_{-4}^{4}\int_{-4}^{u}\dfrac{\sqrt{u-v}}{\sqrt{2}}\dfrac{1}{2\sqrt{2}\sqrt{u-v}}\,dv\,du \\ &=\int_{-4}^{4}\int_{-4}^{u}\dfrac{1}{4}\,dv\,du =\dfrac{1}{4}\left(\dfrac{1}{2}8^2\right)= 8 \end{aligned}\] where in the last step we used the area of a triangle.

    gg 

    This problem is more easily done using rectangular coordinates: \[\begin{aligned} M&=\iint \delta\,dA = \int_0^2\int_{-4+y^2}^{4-y^2}y\,dx\,dy \\ &= \int_0^2\left[\rule{0pt}{10pt}yx\right]_{x=-4+y^2}^{4-y^2}\,dy \\ &= \int_0^2y\left(4-y^2 + 4-y^2\right)\,dy \\ &= \int_0^28y-2y^3\,dy \\ &= \left[4y^2-\dfrac{y^4}{2}\right]_0^2=8 \\ \end{aligned}\]

  34. Find the volume of the piece of the ellipsoid \(x^2+y^2+\dfrac{z^2}{4}=1\) above the plane \(z=1\).

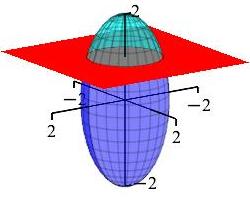
    The plot shows an ellipsoid crossing the x axis at plus and minus 1, the y axis at plus and minus 1, and the z axis plus and minus 2. A horizontal plane crosses through at at z = 1. The solid above the plane is colored a different color.

    Use cylindrical coordinates.

    \(\displaystyle V = \dfrac{5\pi}{12}\)

    We use cylindrical coordinates: \[ x=r\cos\theta \qquad y=r\sin\theta \qquad z=z \] So, the ellipsoid becomes: \[\begin{aligned} r^2 = 1-\dfrac{z^2}{4} \end{aligned}\] The lower \(z\) bound is \(z=1\). To get the upper \(z\) bound, we plug \(r=0\) into the ellipsoid to get \(z=2\). So, the volume is the triple integral: \[\begin{aligned} V&=\iiint 1dV = \int_{0}^{2\pi}\int_{1}^{2}\int_{0}^{\sqrt{1-z^2/4\,}}r\,dr\,dz\,d\theta\\ &= 2\pi\int_{1}^{2}\left[\dfrac{r^2}{2}\right]_{r=0}^{\sqrt{1-z^2/4\,}}\,dz\\ &= \pi\int_{1}^{2}\left(1-\dfrac{z^2}{4}\right)\,dz = \pi\left[z-\dfrac{z^3}{12}\right]_{1}^{2}\\ &= \pi\left[2-\dfrac{8}{12} - 1 + \dfrac{1}{12}\right] = \dfrac{5\pi}{12}\\ \end{aligned}\]

    gg 

  35. Find the volume above the upper half of the hyperboloid \(z^2=1+x^2+y^2\) below the plane \(z=\sqrt{2}\).

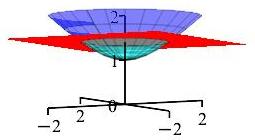
    The plot shows the upper half of an hyperboloid crossing the z axis at z = 1. A horizontal plane crosses through at at z = square root of 2. The solid below the plane is colored a different color.

    Use cylindrical coordinates.

    \(V=\dfrac{2\pi}{3}-\dfrac{\pi}{3}\sqrt{2}\)

    We use cylindrical coordinates. Our \(z\) bounds are \(1\le z \le \sqrt{2}\). Our \(\theta\) bounds are \(0 \le \theta\le 2\pi\). Our \(r\) bounds are \(0 \le r\le \sqrt{z^2-1}\). So we set up a triple integral: \[\begin{aligned} V&=\iiint 1dV = \int_0^{2\pi}\int_{1}^{\sqrt{2}}\int_{0}^{\sqrt{z^2-1}}r\,drdzd\theta\\ &=2\pi\int_{1}^{\sqrt{2}}\int_{0}^{\sqrt{z^2-1}}r\,drdz\\ &=2\pi\int_{1}^{\sqrt{2}}\left.\dfrac{1}{2}r^2\right|_{0}^{r=\sqrt{z^2-1}} \,dz\\ &=2\pi\int_{1}^{\sqrt{2}}\dfrac{1}{2}\left(z^2-1\right)\,dz\\ &=\pi\left[\dfrac{z^3}{3}-z\right]_{1}^{\sqrt{2}} \\ &= \pi\left(\dfrac{2\sqrt{2}}{3}-\sqrt{2}-\dfrac{1}{3}+1\right) =\dfrac{2\pi}{3}-\dfrac{\pi}{3}\sqrt{2} \end{aligned}\]

    gg 

© MYMathApps

Supported in part by NSF Grant #1123255