21. Multiple Integrals in Curvilinear Coordinates

c. Integrating in Spherical Coordinates

The extension of integration to spherical coordinates in 3D is similar to the extension to cylindrical coordinates. We break up the region of integration \(R\) into subregions \(R_k\) which are spherical grid cells. We need to know the volume of these cells.

1. Grid Cells

A spherical box is harder to visualize than a polar rectangle or a cylindrical box. Think of a rectangle on the surface of the earth between two lines of lattitude and between two lines of longitude. Pile up dirt on this rectangle to some depth and that is a spherical box.

A spherical box or spherical grid cell is a region of the form: \[ \rho_1 \le \rho \le \rho_2 \quad \phi_1 \le \phi \le \phi_2 \quad \text{and} \quad \theta_1 \le \theta \le \theta_2 \] The coordinate center of the cell is at: \[ \bar{\rho}=\dfrac{\rho_1+\rho_2}{2} \quad \bar{\phi}=\dfrac{\phi_1+\phi_2}{2} \quad \text{and} \quad \bar{\theta}=\dfrac{\theta_1+\theta_2}{2} \] and the coordinate dimensions of the cell are: \[ \Delta\rho=\rho_2-\rho_1 \quad \Delta\phi=\phi_2-\phi_1 \quad \text{and} \quad \Delta\theta=\theta_2-\theta_1 \]

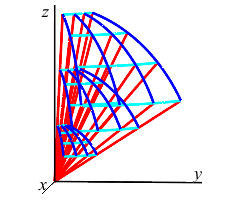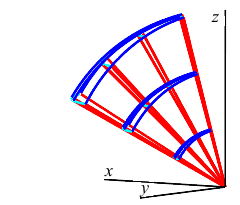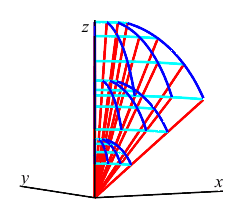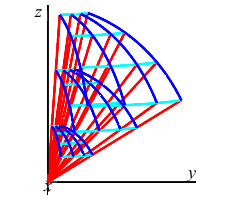
The plot shows a grid of spherical boxes. It has 4 rows of 4 radial lines, 3 layers of 4 lines of latitude and 3 layers of 4 lines of longitude. All together, they form the edges of 9 spherical boxes. It is rotating about the z axis.

It is difficult to derive an exact formula for the volume of a spherical box. However, it is approximately: \[ \Delta V\approx\bar{\rho}\,^2\sin\bar{\phi}\,\Delta\rho\,\Delta\phi\,\Delta\theta \]

Spherical Box

The coordinate dimensions of the box are \(\Delta\rho\), \(\Delta\phi\) and \(\Delta\theta\), but these are not the geometrical lengths. The coordinate dimensions are the same for every box, but the geometrical lengths change from place to place. Let \(L_\rho\), \(L_\phi\) and \(L_\theta\) be the geometrical lengths. Then the volume is approximately: \[ \Delta V\approx L_\rho L_\phi L_\theta \] Notice from the picture that as \(\rho\) gets bigger (we move away from the origin), \(L_\rho\) does not change, but \(L_\phi\) and \(L_\theta\) get longer. Similarly, as \(\phi\) gets bigger (we move away from the north pole), \(L_\rho\) and \(L_\phi\) do not change, but \(L_\theta\) starts at \(0\) the north pole, gets longer until we reach the equator but then gets shorter until it gets to \(0\) again at the south pole. Finally, as \(\theta\) changes, \(L_\rho\), \(L_\phi\) and \(L_\theta\) do not change. So the lengths appear to change according to: \[ L_\rho=\Delta\rho \qquad L_\phi=\rho\Delta\phi \qquad L_\theta=\rho\sin\phi\Delta\theta \] Combining these we have: \[ \Delta V\approx \rho^2\sin\phi\,\Delta\rho\,\Delta\phi\,\Delta\theta \]

In the limit as \(\Delta\rho\), \(\Delta\phi\) and \(\Delta\theta\) get small, \(\Delta\rho\) becomes \(d\rho\), \(\Delta\phi\) becomes \(d\phi\), \(\Delta\theta\) becomes \(d\theta\) and \(\Delta V\) becomes \(dV\). Consequently:

The spherical differential of volume is: \[ dV=\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \]

Memorize this!

We will derive this formula for the spherical volume differential as a special case of the volume differential for general curvilinear coordinates in 3D later in this chapter. For now, we will just use the formula to do integrals starting on the next page.

© MYMathApps

Supported in part by NSF Grant #1123255