21. Multiple Integrals in Curvilinear Coordinates

b. Integrating in Cylindrical Coordinates

The extension of triple integrals to cylindrical coordinates is very similar to the extension of double integrals to polar coordinates. We will break up the region of integration \(R\) into subregions \(R_k\) which are cylindrical grid cells. So we need to know the volume of these cells.

1. Grid Cells

A cylindrical box is similar to the polar rectangle except there is an additional \(z\) coordinate.

The cells look like a tower whose base is a polar grid cell. The base is marked off by two radial lines and two pieces of circles, and then this area is extended upwards to the value of \(z\).

A cylindrical box or cylindrical grid cell is a region of the form: \[ r_1 \le r \le r_2 \quad \theta_1 \le \theta \le \theta_2 \quad \text{and} \quad z_1 \le z \le z_2 \] See the figure at the right. The coordinate center of the cell is at: \[ \bar{r}=\dfrac{r_1+r_2}{2} \quad \bar{\theta}=\dfrac{\theta_1+\theta_2}{2} \quad \text{and} \quad \bar{z}=\dfrac{z_1+z_2}{2} \] and the coordinate dimensions of the cell are: \[ \Delta r=r_2-r_1 \quad \Delta\theta=\theta_2-\theta_1 \quad \text{and} \quad \Delta z=z_2=z_1 \]

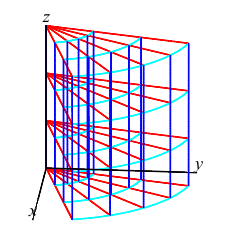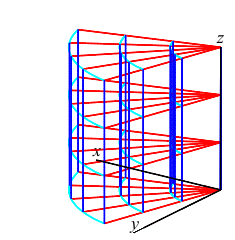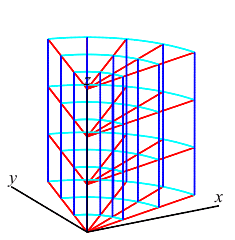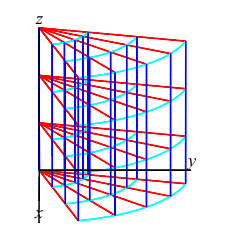
Since the base of the box is a polar rectangle of area \(\Delta A=\bar{r}\,\Delta r\Delta\theta\) and the height is \(\Delta z\), we conclude:

The volume of a cylindrical box is: \[ \Delta V=\bar{r}\,\Delta r\Delta\theta\Delta z \]

In the limit as \(\Delta r\), \(\Delta\theta\) and \(\Delta z\) get small, \(\Delta r\) becomes \(dr\), \(\Delta\theta\) becomes \(d\theta\), \(\Delta z\) becomes \(dz\) and \(\Delta V\) becomes \(dV\). Consequently:

The cylindrical differential of volume is: \[ dV=r\,dr\,d\theta\,dz \]

Memorize this!

We will see how the differential of volume is used in integrals on the next page.

21. Multiple Integrals in Curvilinear Coordinates

b. Integrating in Cylindrical Coordinates

1. Grid Cells

Heading