21. Multiple Integrals in Curvilinear Coordinates

e. Integrating in 3D Curvilinear Coordinates

4. Ellipsoid Example

Below is an example of using 3D curvilinear coordinates to compute an integral over an ellipsoid.

We first write the ellipsoid in standard form: \[ \dfrac{x^2}{36}+\dfrac{y^2}{9}+\dfrac{z^2}{4}=1 \] There are two reasonable coordinate systems to use:

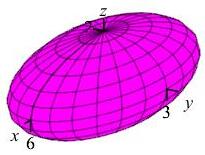
Use the coordinate system given by the component equations \(x=6u\), \(y=3v\) and \(z=2w\) or the vector equation \((x,y,z)=\vec{R}(u,v,w)=(6u,3v,2w)\). The benefit of this coordinate system is that it converts the equation of the ellipsoid into the equation for the sphere \[ u^2+v^2+w^2=1 \] So the region of integration changes from \(R\), the interior of an ellipsoid in the \(xyz\)-space, to \(R'\), the interior of a sphere in the \(uvw\)-space which can be integrated in spherical coordinates. For this coordinate system, the Jacobian is \[ J=\left|\dfrac{\partial(x,y,z) }{\partial(u,v,w) }\right| =\left| \begin{vmatrix} \dfrac{\partial x}{\partial u}&\dfrac{\partial y}{\partial u}&\dfrac{\partial z}{\partial u} \\[6pt] \dfrac{\partial x}{\partial v}&\dfrac{\partial y}{\partial v}&\dfrac{\partial z}{\partial v} \\[6pt] \dfrac{\partial x}{\partial w}&\dfrac{\partial y}{\partial w}&\dfrac{\partial z}{\partial w} \end{vmatrix} \right|=\left| \begin{vmatrix} 6 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 2 \end{vmatrix} \right|=36 \] So the integral becomes \[ \iiint\limits_R z^2\,dV =\iiint\limits_{R'} z^2\,J\,du\,dv\,dw =\iiint\limits_{u^2+v^2+w^2 \le 1}(2w)^2 36\,du\,dv\,dw \] We now switch to spherical coordinates, \[ u=\rho\sin\phi\cos\theta \qquad v=\rho\sin\phi\sin\theta \qquad \text{and} \qquad w=\rho\cos\phi \] for which the differential of volume is \(du\,dv\,dw=\rho^2\sin\phi\,d\rho\,d\phi\,d\theta\). So the integral becomes \[\begin{aligned} \iiint\limits_R z^2\,dV &=144\int_0^{2\pi}\int_0^\pi\int_0^1 (\rho\cos\phi)^2\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=144\int_0^{2\pi} 1\,d\theta\int_0^\pi \cos^2\phi\sin\phi\,d\phi\int_0^1\rho^4 \,d\rho \\ &=144(2\pi) \left[-\,\dfrac{\cos^3\theta}{3}\right]_0^\pi \left[\dfrac{\rho^5}{5}\right]_0^1 \\ &=96\pi(-(-1)^3+(1)^3) \left(\dfrac{1}{5}\right) =\dfrac{192\pi}{5} \end{aligned}\]

---

Rather than do two successive coordinate transformations, from \((x,y,z)\) to \((u,v,w)\) to \((\rho,\phi,\theta)\), we can do it all at once. We use an ellipsoidal spherical coordinate system, given by the component equations, \[ x=6\rho\sin\phi\cos\theta \qquad y=3\rho\sin\phi\sin\theta \qquad \text{and} \qquad z=2\rho\cos\phi \] or by the vector equation \[ (x,y,w)=\vec{R}(\rho,\phi,\theta) =(6\rho\sin\phi\cos\theta,3\rho\sin\phi\sin\theta,2\rho\cos\phi) \] The Jacobian is \[ J=\left|\dfrac{\partial(x,y,z) }{\partial(\rho,\phi,\theta) }\right| =\left| \begin{vmatrix} \dfrac{\partial x}{\partial\rho} &\dfrac{\partial y}{\partial\rho} &\dfrac{\partial z}{\partial\rho} \\[6pt] \dfrac{\partial x}{\partial\phi} &\dfrac{\partial y}{\partial\phi} &\dfrac{\partial z}{\partial\phi} \\[6pt] \dfrac{\partial x}{\partial\theta}&\dfrac{\partial y}{\partial\theta}&\dfrac{\partial z}{\partial\theta} \end{vmatrix} \right|=\cdots=36\rho^2\sin\phi \] So the integral is \[\begin{aligned} \iiint_R &z^2\,dV =\iiint\limits_R z^2\,dV =\iiint_R z^2\,J\,d\rho\,d\phi\,d\theta \\ &=\int_0^{2\pi}\int_0^\pi\int_0^1 (2\rho\cos\phi)^2 36\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\cdots=\dfrac{192\pi}{5} \end{aligned}\]

Obviously, method 1 is easier since we don't need to compute a hard Jacobian. However, it is important to know it can be done the other way.

Notice that while we used the letters \(\rho\), \(\phi\) and \(\theta\) in both methods, they do NOT measure the radius, polar angle and the azimuthal angle in the \(xyz\)-space.

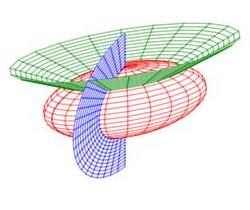
There are more exercises using ellipsoidal spherical coordinates on the next page.