21. Multiple Integrals in Curvilinear Coordinates
c. Integrating in Spherical Coordinates
3. Applications
Integrals in spherical coordinates are particularly useful when the integrand and/or the limits of integration are spherically symmetric or involve spheres or cones. We previously did Applications of Triple Integrals in rectangular coordinates and Applications of Triple Integrals in cylindrical coordinates. All of those applications can also be done using spherical coordinates.
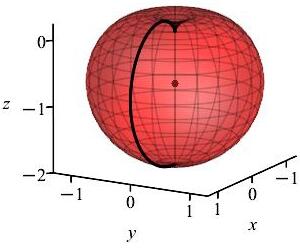
All the examples on this page of applications of triple integrals in spherical coordinates will use the apple shape shown in the plot. The surface is given in spherical coordinates by \(\rho=1-\cos\phi\) which is a cardioid in any plane through the \(z\)-axis. Find the bounds on the integrals in spherical coordinates.
The volume goes all the way around in the \(\theta\) direction (as shown by the white line), from the north pole to the south pole in the \(\phi\) direction (as shown by the black line) and from the origin to the surface in the \(\rho\) direction. So the limits are: \[ 0 \le \theta \le 2\pi \qquad 0 \le \phi \le \pi \qquad 0 \le \rho \le 1-\cos\phi \]
Volume
To find the volume of a 3D region \(R\) in spherical coordinates, the differential of volume \(dV\) must be expressed in spherical coordinates: \[ \text{Volume}=\iiint_R 1\,dV =\iiint_R \rho^2\sin\phi\,d\rho\,d\phi\,d\theta \]
Find the volume of the apple.
Mass
To find the mass of a 3D region \(R\) in spherical coordinates, the density \(\delta\) must also be expressed in spherical coordinates: \[ M=\iiint_R \delta(x,y,z)\,dV =\iiint_R \delta(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \]
Find the mass of the apple if its mass density is \(\delta=x^2+y^2\).
Center of Mass
To find the center of mass of a 3D region \(R\) in spherical coordinates, the coordinates \(x\), \(y\) and \(z\) must also be expressed in spherical coordinates. So the center of mass is: \[ \bar{x}=\dfrac{M_x}{M} \quad \text{and} \quad \bar{y}=\dfrac{M_y}{M} \quad \text{and} \quad \bar{z}=\dfrac{M_z}{M} \] where the mass of the region is \[ M=\iiint_R \delta(x,y,z)\,dV =\iiint_R \delta(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \] and the \(x\), \(y\) and \(z\) \(1^\text{st}\)-moments of the mass, respectively, are \[\begin{aligned} M_x&=\iiint_R x\,\delta(x,y,z)\,dV =\iiint_R \rho\sin\phi\cos\theta\,\delta(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ M_y&=\iiint_R y\,\delta(x,y,z)\,dV =\iiint_R \rho\sin\phi\sin\theta\,\delta(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ M_z&=\iiint_R z\,\delta(x,y,z)\,dV =\iiint_R \rho\cos\phi\,\delta(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \end{aligned}\]
It is important to remember that we cannot compute \(\bar{\rho}=\dfrac{M_\rho}{M}\), \(\bar{\phi}=\dfrac{M_\phi}{M}\) and \(\bar{\theta}=\dfrac{M_\theta}{M}\) where \[\text{\Large\textcolor{red}Wrong}\qquad \begin{array}{rl} M_\rho&=\displaystyle\iiint_R \rho\,\delta(\rho,\phi,\theta)\,dV \\[8pt] M_\phi&=\displaystyle\iiint_R \phi\,\delta(\rho,\phi,\theta)\,dV \\[8pt] M_\theta&=\displaystyle\iiint_R \theta\,\delta(\rho,\phi,\theta)\,dV \end{array} \qquad \text{\Large\textcolor{red}Wrong} \] because moments are only defined for rectangular coordinates since the balance beam derivation (\(\text{Torque} = \text{Force} \times \text{Lever Arm}\)) does not work for the \(r\) and \(\theta\) directions. If we want the spherical coordinates, \((\bar \rho,\bar\phi,\bar\theta)\) of the center of mass, we must first find the rectangular components and then convert to spherical.
Find the center of mass of the apple if its mass density is \(\delta=x^2+y^2\).
Centroid
The centroid of a region \(R\) in 3D is the same as the center of mass but with constant density which we take as \(\delta=1\). Then the mass reduces to the volume and the moments of mass become moments of volume. Thus the centroid is: \[ \bar{x}=\dfrac{V_x}{V} \quad \text{and} \quad \bar{y}=\dfrac{V_y}{V} \quad \text{and} \quad \bar{z}=\dfrac{V_z}{V} \] where \(V\) is the volume and the \(x\), \(y\) and \(z\) \(1^\text{st}\)-moments of the volume, respectively, are \[\begin{aligned} V_x&=\iiint_R x\,dV =\iiint_R \rho\sin\phi\cos\theta\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ V_y&=\iiint_R y\,dV =\iiint_R \rho\sin\phi\sin\theta\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ V_z&=\iiint_R z\,dV =\iiint_R \rho\cos\phi\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \end{aligned}\]
Find the centroid of the apple.
Average Value
To find the average value of a function over a 3D region in spherical coordinates, the function must be evaluated in spherical coordinates before integrating: \[ f_\text{ave}=\dfrac{1}{V}\iiint_R f(x,y,z)\,dV =\dfrac{1}{V}\iiint_R f(\rho,\phi,\theta)\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \]
Compute the average of the temperature, \(T=270-z\), within the apple.
4-Volume (Optional)
If \(f(x,y,z)\) and \(g(x,y,z)\) are functions on a region \(R\) in \(3\)-space and \(f(x,y,z) \ge g(x,y,z)\), then the 4-volume above the \(3\)-dimensional region \(R\) between \(w=g(x,y,z)\) and \(w=f(x,y,z)\) is: \[\begin{aligned} V_4&=\iiint_R f(x,y,z)-g(x,y,z)\,dV \\ &=\iiint_R (f(\rho, \phi,\theta)-g(\rho, \phi,\theta))\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \end{aligned}\]
The base of a \(4\)-dimensional solid is the apple discussed above. The upper surface is the graph of the function \(w=2+z\). (Of course, the lower surface is \(w=0\).) Find the \(4\)-volume of this \(4\)-dimensional solid.
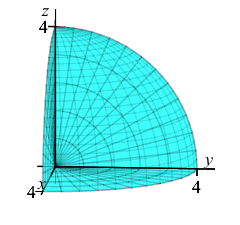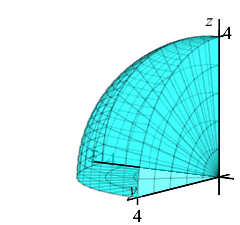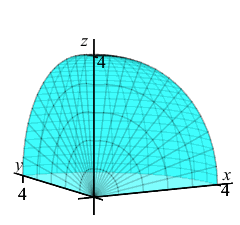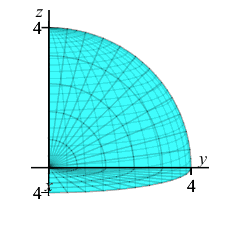
The exercises on the rest of this page refer \(8^\text{th}\) of a sphere in the first octant of radius \(4\). Find the limits of integration.
The volume and centroid were found in a previous example using rectangular coordinates. These computations are much easier using spherical coordinates.
\(0 \le r \le 4\)
\(0 \le \phi \le \dfrac{\rule{0pt}{12pt}\pi}{2}\)
\(0 \le \theta \le \dfrac{\rule{0pt}{12pt}\pi}{2}\)
The \(8^\text{th}\) of a sphere is a quarter circle in both the \(\phi\) and \(\theta\). So the limits are: \[ 0 \le \phi \le \dfrac{\pi}{2} \qquad 0 \le \theta \le \dfrac{\pi}{2} \] Since the radius is \(4\), the limits are: \[ 0 \le r \le 4 \]
Find the volume of the \(8^\text{th}\) of a sphere.
\(V=\dfrac{32}{3}\pi\)
The volume is: \[\begin{aligned} V&=\iiint 1\,dV =\int_0^{\pi/2}\int_0^{\pi/2}\int_0^{4} \rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\left[\theta\dfrac{}{}\right]_0^{\pi/2}\left[-\cos\phi\dfrac{}{}\right]_0^{\pi/2} \left[\dfrac{\rho^3}{3}\right]_0^4 \\ &=\dfrac{\pi}{2}(--1)\dfrac{4^3}{3} =\dfrac{32}{3}\pi \end{aligned}\]
Since this is an 8th of a sphere of radius \(4\), the high school geometry formula gives: \[ V=\dfrac{1}{8}\left(\dfrac{4}{3}\pi r^3\right) =\dfrac{1}{8}\left(\dfrac{4}{3}\pi 4^3\right) =\dfrac{32}{3}\pi \] which agrees with our result.
Find the mass of the \(8^\text{th}\) of a sphere if the density is \(\delta=x^2+y^2+z^2\).
\(M=\dfrac{512}{5}\pi\)
In spherical coordinates, the density is \(\delta=x^2+y^2+z^2=\rho^2\). So the mass is: \[\begin{aligned} M&=\iiint \delta\,dV =\int_0^{\pi/2}\int_0^{\pi/2}\int_0^{4} (\rho^2) \rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\dfrac{\pi}{2}\left[-\cos\phi\dfrac{}{}\right]_0^{\pi/2} \left[\dfrac{\rho^5}{5}\right]_0^4 \\ &=\dfrac{\pi}{2}(--1)\dfrac{4^5}{5} =\dfrac{512}{5}\pi \end{aligned}\]
Find the center of mass of the \(8^\text{th}\) of a sphere if the density is \(\delta=x^2+y^2+z^2\).
\((\bar{x},\bar{y},\bar{z}) =\left(\dfrac{5}{3},\dfrac{5}{3},\dfrac{5}{3}\right)\)
We have already found the mass of the region, so now we compute the \(x\),\(y\), and \(z\) moments of mass for the region. By symmetry, they should all yield the same result; therefore, we will simply compute \(\bar{z}\). Recall that \(z=\rho\cos\phi\) and \(\delta=x^2+y^2+z^2=\rho^2\). \[\begin{aligned} M_z&=\iiint\limits_R z\,\delta\,dV =\int_0^{\pi/2}\int_0^{\pi/2}\int_0^4 (\rho\cos\phi)(\rho^2) \rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\int_0^{\pi/2} \,d\theta \int_0^{\pi/2} \cos\phi\sin\phi \int_0^4 \rho^5\,d\rho \\ &=\left[\theta\right]_0^{\pi/2} \left[\dfrac{\sin^2\phi}{2}\right]_0^{\pi/2} \left[\dfrac{\rho^6}{6}\right]_0^4 =\dfrac{\pi}{2}\dfrac{1}{2}\dfrac{4^6}{6} =\dfrac{512}{3}\pi \end{aligned}\] We conclude: \[ M_z=M_y=M_x=\dfrac{512}{3}\pi \]
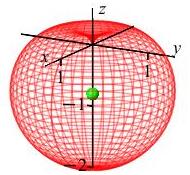
Finally, we compute the center of mass: \[ \bar{x}=\bar{y}=\bar{z} =\dfrac{M_z}{M}=\dfrac{512\pi}{3}\dfrac{5}{512\pi} =\dfrac{5}{3} \] Thus the center of mass for this region with density \(\delta=\rho^2\) is \[ (\bar{x},\bar{y},\bar{z}) =\left(\dfrac{5}{3},\dfrac{5}{3},\dfrac{5}{3}\right) \] The plot shows the center of mass as a blue diamond in the middle.
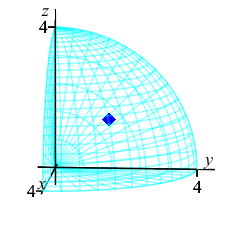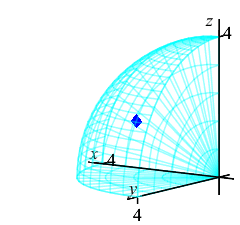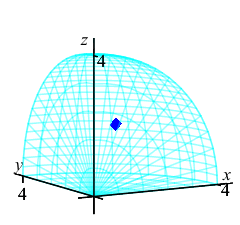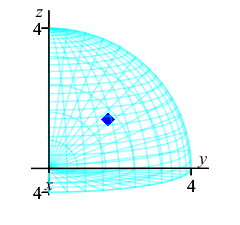
We know the center of mass is within the region because \[ \sqrt{\bar{x}^2+\bar{y}^2+\bar{z}^2}\approx 2.89 \lt 4=\rho \]
Find the centroid of the \(8^\text{th}\) of a sphere.
\((\bar{x},\bar{y},\bar{z}) =\left(\dfrac{3}{2},\dfrac{3}{2}\dfrac{3}{2}\right)\)
The computation is similar to that for the center of mass except that now \(\delta=1\). Again, by symmetry, all components of the centroid will be equal. Thus we only compute the \(z\) component. \[\begin{aligned} V_z&=\iiint\limits_R z\,dV =\int_0^{\pi/2}\int_0^{\pi/2}\int_0^4 (\rho\cos\phi) \rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\int_0^{\pi/2} \,d\theta \int_0^{\pi/2} \cos\phi\sin\phi\,d\phi \int_0^4 \rho^3\,d\rho\\ &=\dfrac{\pi}{2} \left[\dfrac{\sin^2\phi}{2}\right]_0^{\pi/2} \left[\dfrac{\rho^4}{4}\right]_0^4 =\dfrac{\pi}{2} \dfrac{1}{2} 64 =16\pi \end{aligned}\] We already know the total volume of the region, thus we compute the centroid as \[ \bar{x}=\bar{y}=\bar{z}=\dfrac{V_z}{V} =\dfrac{3}{32\pi}16\pi=\dfrac{3}{2} \]
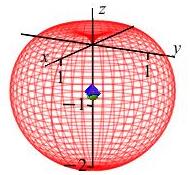
We already know the total volume of the region, thus we compute the centroid as \[ \bar{x}=\bar{y}=\bar{z}=\dfrac{V_z}{V} =\dfrac{3}{32\pi}16\pi=\dfrac{3}{2} \] The plot shows the centroid as a red sphere in the middle.
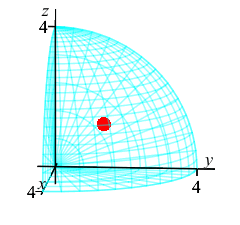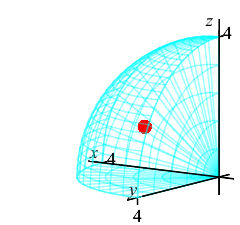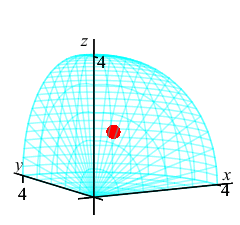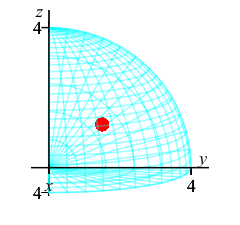
We know the center of mass is within the region because \[\begin{aligned} \sqrt{\bar{x}^2+\bar{y}^2+\bar{z}^2} &=\sqrt{\left(\dfrac{3}{2}\right)^2+\left(\dfrac{3}{2}\right)^2 +\left(\dfrac{3}{2}\right)^2} \\ &=\sqrt{\dfrac{27}{4}}\approx 2.6 \lt 4=\rho \end{aligned}\]
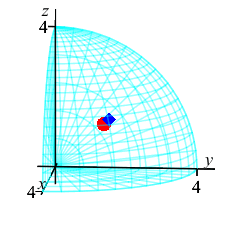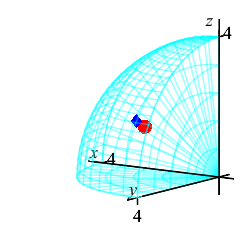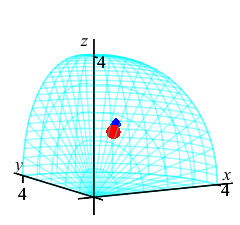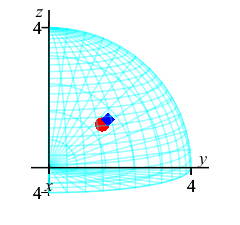
This plot shows the center of mass as well as the centroid.
The center of mass is plotted as a blue diamond.
The centroid at is plotted as a red sphere.
Notice that the center of mass is farther from the origin because the
density, \(\delta=\rho^2\), is bigger near the surface of the sphere.
Notice how much easier this computation was as compared to the rectangular integral done in a previous example.
Compute the average of the temperature, \(T=z\), over the \(8^\text{th}\) of a sphere.
\(T_\text{ave}=\dfrac{3}{2}\)
We have already computed the volume \(V=\dfrac{32}{3}\pi\). In spherical coordinates, the temperature is \(T=z=\rho\cos\phi\). So the integral of the temperature is: \[\begin{aligned} \iiint T\,dV &=\int_0^{\pi/2}\int_0^{\pi/2}\int_0^{4} (\rho\cos\phi)\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \\ &=\dfrac{\pi}{2}\left[\dfrac{\sin^2\phi}{2}\right]_0^{\pi/2} \left[\dfrac{\rho^4}{4}\right]_0^4 \\ &=\dfrac{\pi}{2}\dfrac{1}{2}\dfrac{4^4}{4} =16\pi \end{aligned}\] And the average temperature is: \[ T_\text{ave}=\dfrac{1}{V}\iiint T\,dV =\dfrac{3}{32\pi}16\pi =\dfrac{3}{2} \]
(Optional) Find the \(4\)-volume of the \(16^\text{th}\) of the \(4\)-dimensional sphere of radius \(4\), \(x^2+y^2+z^2+w^2=16\), which has all positive coordinates. The \(3\)-dimensional base has \(w=0\). So it is the \(8^\text{th}\) of a sphere described above. Its upper surface is \(w=\sqrt{16-x^2-y^2-z^2}\).
\(V_4=8\pi^2\)
In spherical coordinates, the upper surface is \[ w=\sqrt{16-\rho^2} \] So the \(4\)-volume is: \[\begin{aligned} V_4&=\iiint_R w(\rho,\phi,\theta)\,dV \\ &=\int_0^{\pi/2}\int_0^{\pi/2}\int_0^{4} \sqrt{16-\rho^2}\,\rho^2\sin\phi\,d\rho\,d\phi\,d\theta \end{aligned}\] The \(\phi\) and \(\theta\) integrals are easy: \[\begin{aligned} V_4&=\int_0^{\pi/2}\sin\phi\,d\phi \int_0^{\pi/2}\,d\theta \int_0^{4}\sqrt{16-\rho^2}\,\rho^2\,d\rho \\ &=\left[\rule{0pt}{10pt}-\cos\phi\right]_0^{\pi/2} \left[\rule{0pt}{10pt}\theta\right]_0^{\pi/2} \int_0^{4}\sqrt{16-\rho^2}\,\rho^2\,d\rho \\ &=\dfrac{\pi}{2}\int_0^{4}\sqrt{16-\rho^2}\,\rho^2\,d\rho \\ \end{aligned}\] The \(\rho\) integral needs the trig substitution \(\rho=4\sin\alpha\) and \(d\rho=4\cos\alpha\,d\alpha\): \[\begin{aligned} V_4&=\dfrac{\pi}{2}\int_0^{\pi/2}\sqrt{16-16\sin^2\alpha} \,16\sin^2\alpha\,4\cos\alpha\,d\alpha \\ &=128\pi\int_0^{\pi/2}\sin^2\alpha\cos^2\alpha\,d\alpha =32\pi\int_0^{\pi/2}\sin^2(2\alpha)\,d\alpha \\ &=16\pi\int_0^{\pi/2}(1-\cos(4\alpha))\,d\alpha =16\pi\left[\alpha-\dfrac{\sin(4\alpha)}{4}\right]_0^{\pi/2} \\ &=16\pi\dfrac{\pi}{2} =8\pi^2 \end{aligned}\]
The 4-volume of a general \(4\)-sphere of radius \(R\) is \(V_4=\dfrac{1}{2}\pi^2R^4\). (You are not expected to know this.) So the volume of a \(16^\text{th}\) of a \(4\)-sphere of radius \(4\) is \[ V_4=\dfrac{1}{16}\left(\dfrac{1}{2}\pi^2 4^4\right)=8\pi^2 \]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum