21. Multiple Integrals in Curvilinear Coordinates

a. Integrating in Polar Coordinates

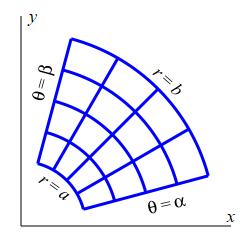
2. Integral over a Polar Rectangle

Recall the Riemann sum definition of a double integral, and its formulation for a rectangle in rectangular coordinates. We now formulate it for a polar rectangle in polar coordinates.

If \(R\) is the polar rectangle \([a,b]\times[\alpha,\beta]\), then \[\begin{aligned} \iint\limits_R f(x,y)\,dA &=\int_\alpha^\beta\int_a^b f(r,\theta)\,r\,dr\,d\theta \\ &=\int_a^b\int_\alpha^\beta f(r,\theta)\,r\,d\theta\,dr \end{aligned}\] In particular, for a polar rectangle, the iterated integral with constant limits is independent of the order of integration.

The plot shows arcs of several concentric circles and pieces of several
radial lines. They form a 4 by 4 grid of boxes.

(1) These are just the iterated integrals computed by holding the outer variable fixed while doing the inner integral and then completing the outer integral.
(2) In these formulas, the important thing to remember is that the differential of area is \[ dA=r\,dr\,d\theta \] and \(r\) becomes part of the integrand when we compute the \(r\) integral.
(3) If we reverse the order of the differentials, we must also reverse the limits on the integrals.

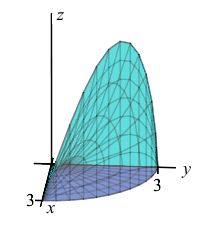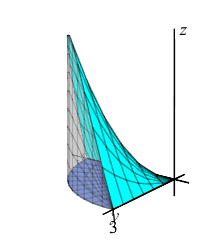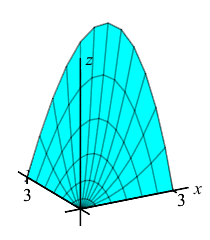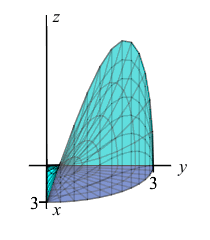
Find the volume under the piece of the paraboloid \(z=x^2+y^2\) above the circle \(x^2+y^2 \le 9\).

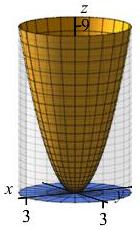
The plot shows the solid below a paraboloid above a circle.
Note: The solid is outside the paraboloid, not inside. So the outside of
the solid is a cylinder.

The volume is the double integral: \[ V=\iint\limits_R (x^2+y^2)\,dA \] To compute it, we write \(dA\) and \(x\) and \(y\) in polar coordinates: \[ dA=r\,dr\,d\theta \qquad x=r\cos\theta \qquad y=r\sin\theta \] So the volume may be computed as the iterated integral: \[\begin{aligned} V&=\int_0^{2\pi}\int_0^3 (x^2+y^2)\,r\,dr\,d\theta =\int_0^{2\pi}\int_0^3 r^3\,dr\,d\theta \\ &=\int_0^{2\pi} 1\,d\theta\int_0^3 r^3\,dr =2\pi\left[\dfrac{r^4}{4}\right]_0^3 =\dfrac{81\pi}{2} \end{aligned}\]

In rectangular coordinates, this would be: \[ V=\int_{-3}^3\int_{-\sqrt{9-x^2}}^{\sqrt{9-x^2}} (x^2+y^2)\,dy\,dx \] which would be much harder to compute.

Find the volume under the hyperboloid \(z=xy\) above the quarter circle \(x^2+y^2 \le 9\) in the first quadrant.

The plot shows the volume below the hyperboloid z equals x y above
the quarter circle of radius 4in the first quadrant. It is rotating
so one can see different sides.

\(\displaystyle V=\int_0^{\pi/2}\int_0^3 r^3\sin\theta\cos\theta\,dr\,d\theta =\dfrac{81}{8}\)

The quarter circle in the first quadrant satisfies \(0 \le \theta \le \dfrac{\pi}{2}\). So the volume is: \[\begin{aligned} V&=\int_0^{\pi/2}\int_0^3 (xy)\,r\,dr\,d\theta =\int_0^{\pi/2}\int_0^3 r^3\sin\theta\cos\theta\,dr\,d\theta \\ &=\int_0^3 r^3\,dr\int_0^{\pi/2} \sin\theta\cos\theta\,\,d\theta =\left[\dfrac{r^4}{4}\right]_0^3\left[\dfrac{\sin^2\theta}{2}\right]_0^{\pi/2} \\ &=\dfrac{81}{4}\left(\dfrac{1}{2}\right)=\dfrac{81}{8} \end{aligned}\]

21. Multiple Integrals in Curvilinear Coordinates

a. Integrating in Polar Coordinates

2. Integral over a Polar Rectangle

Heading