21. Multiple Integrals in Curvilinear Coordinates

d. Integrating in 2D Curvilinear Coordinates

6. Applications

We previously did Applications of Multiple Integrals in Rectangular Coordinates and we have done Applications of Double Integrals in Polar Coordinates. All of those applications can also be done using general two-dimensional curvilinear coordinates.

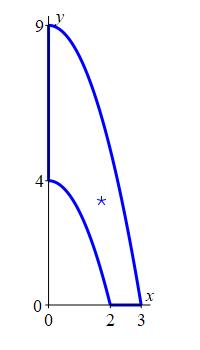
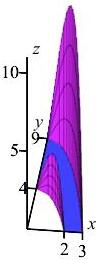
All the examples on this page of applications of double integrals in curvilinear coordinates will use the region between the paraboloids \(y=9-x^2\) and \(y=4-x^2\) in the first quadrant. Besides the two parabolas, the other \(2\) boundaries are the \(x\)-axis (\(y=0\)) and the \(y\)-axis (\(x=0\)). Find a curvilinear coordinate system for the region. Then find the Jacobian factor and the ranges of the coordinates to describe the solid.

The plot shows the region in the first quadrant between 2 parabolas. One has its vertex at y = 9 on the y axis and crosses the x axis at x = 3. The other has its vertex at y = 4 on the y axis and crosses the x axis at x = 2.

It seems obvious that we would like to to take one of the curvilinear coordinates to be \(u=y+x^2\) so that the \(2\) parabola edges are \(u=4\) and \(u=9\). But it is not obvious what to take for the other coordinate. For lack of a better choice, we take \(v=y-x^2\).

To compute the Jacobian, we need to solve for \(x\) and \(y\). To do this, we add and subtract the \(2\) equations: \[ u=y+x^2 \quad \text{and} \quad v=y-x^2 \] to get: \[ u+v=2y \quad \text{and} \quad u-v=2x^2 \] So our coordinate system is: \[ x=\dfrac{\sqrt{u-v} }{\sqrt{2}} \quad \text{and} \quad y=\dfrac{u+v}{2} \] From this, we can find the Jacobian factor: \[\begin{aligned} J&=\left|\begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\[8pt] \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix}\right| =\left|\begin{vmatrix} \dfrac{1}{2\sqrt{2}\sqrt{u-v}} & \dfrac{1}{2} \\[8pt] \dfrac{-1}{2\sqrt{2}\sqrt{u-v}} & \dfrac{1}{2} \end{vmatrix}\right| \\ &=\left|\dfrac{1}{4\sqrt{2}\sqrt{u-v}}-\,\dfrac{-1}{4\sqrt{2}\sqrt{u-v}}\right| =\dfrac{1}{2\sqrt{2}\sqrt{u-v}} \end{aligned}\]

Two of the boundaries are \(u=4\) and \(u=9\). The other \(2\) boundaries are:
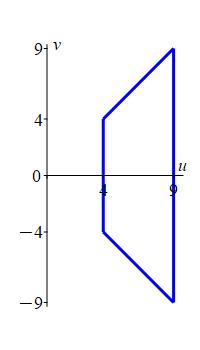
The \(x\)-axis: \[ y=0 \quad \text{or} \quad \dfrac{u+v}{2}=0 \quad \text{or} \quad v=-u \] The \(y\)-axis: \[ x=0 \quad \text{or} \quad\dfrac{\sqrt{u-v}}{\sqrt{2} }=0 \quad \text{or} \quad v=u \] Here is a plot of the region in the \(uv\)-plane. This is a nice region to integrate over. It is Type \(u\). So the \(u\) integral is on the outside.

The plot shows a trapezoid in the uv plane. It has 2 vertical lines at u = 4 and u = 9. The top is the line v = x and the bottom is the line v = -u.

Volume

The volume under the a surface \(z=f(x,y)\) above a region \(R\) is: \[ V=\iint_R f(x,y)\,dA=\iint_R f(u,v)\,J\,du\,dv \]

Find the volume of the solid below the graph of \(f(x,y)=xy\) above region between the parabolas.

The plot shows a solid above the region between the paraboloids. It has vertical sides and a top which slants downward toward the origin.

In terms of \(u\) and \(v\), our function is: \[ f=xy=\dfrac{\sqrt{u-v} }{\sqrt{2}}\dfrac{u+v}{2} =\dfrac{(u+v)\sqrt{u-v}}{2\sqrt{2}} \] The differential of area is: \[ dA=J\,dv\,du=\dfrac{1}{2\sqrt{2}\sqrt{u-v}}\,dv\,du \] So the volume under \(f\) is: \[\begin{aligned} V&=\iint_R f\,dA=\iint_R xyJ\,dv\,du \\ &=\int_4^9\int_{-u}^u \dfrac{(u+v)\sqrt{u-v}}{2\sqrt{2}} \dfrac{1}{2\sqrt{2}\sqrt{u-v}}\,dv\,du \\ &=\dfrac{1}{8}\int_4^9\int_{-u}^u (u+v)\,dv\,du =\dfrac{1}{8}\int_4^9\left[uv+\dfrac{v^2}{2}\right]_{v=-u}^u\,du \\ &=\dfrac{1}{8}\int_4^9\left[\left(u^2+\dfrac{u^2}{2}\right) -\left(-u^2+\dfrac{(-u)^2}{2}\right)\right]\,du \\ &=\dfrac{1}{8}\int_4^9 2u^2\,du =\dfrac{1}{4}\left[\dfrac{u^3}{3}\right]_4^9 =\dfrac{1}{12}(9^3-4^3)=\dfrac{665}{12}\approx55.4 \end{aligned}\]

Area

The area of a region \(R\) is: \[ A=\iint_R 1\,dA=\iint_R J\,du\,dv \]

Find the area of the region between the parabolas.

The area is: \[\begin{aligned} A&=\iint_R \,dA =\int_4^9\int_{-u}^u \dfrac{1}{2\sqrt{2}\sqrt{u-v}}\,dv\,du \\ &=\dfrac{1}{\sqrt{2}}\int_4^9\left[\rule{0pt}{10pt}-\sqrt{u-v}\right]_{v=-u}^u\,du \\ &=\dfrac{1}{\sqrt{2}}\int_4^9 [\sqrt{2u}]\,du =\int_4^9 \sqrt{u}\,du =\left[2\dfrac{u^{3/2}}{3}\right]_4^9 \\ &=2\dfrac{9^{3/2}-4^{3/2}}{3} =2\dfrac{27-8}{3}=\dfrac{38}{3}\approx12.7 \end{aligned}\]

This area could have been found more directly using a single rectangular integral by subtracting the area under the small parabola from the area under the large parabola: \[\begin{aligned} A&=\int_0^3(9-x^2)\,dx-\int_0^2(4-x^2)\,dx \\ &=\left[9x-\dfrac{x^3}{3}\right]_0^3-\left[4x-\dfrac{x^3}{3}\right]_0^2 \\ &=(27-9)-\left(8-\dfrac{8}{3}\right) =\dfrac{38}{3} \end{aligned}\] However, the double integral is essential for all the other applications.

Mass

The mass of a plate occupying a 2D region \(R\) with mass density \(\delta\) is: \[ M=\iint_R \delta(x,y)\,dA=\iint_R \delta(u,v)\,J\,du\,dv \]

Find the mass of the region between the parabolas if the mass density is \(\delta=x\).

The mass is the integral of the density \(\delta=x=\dfrac{\sqrt{u-v}}{\sqrt{2}}\): \[\begin{aligned} M&=\iint_R \delta\,dA=\iint_R xJ\,dv\,du \\ &=\int_4^9\int_{-u}^u \dfrac{\sqrt{u-v}}{\sqrt{2}} \dfrac{1}{2\sqrt{2}\sqrt{u-v}}\,dv\,du \\ &=\dfrac{1}{4}\int_4^9\int_{-u}^u 1\,dv\,du =\dfrac{1}{4}\int_4^9\left[\rule{0pt}{10pt}v\right]_{v=-u}^u\,du \\ &=\dfrac{1}{4}\int_4^92u\,du =\dfrac{1}{4}\left[\rule{0pt}{10pt}u^2\right]_4^9 =\dfrac{1}{4}(9^2-4^2)=\dfrac{65}{4}\approx16.24 \end{aligned}\]

Center of Mass

The center of mass of a plate occupying a region \(R\) with mass density \(\delta\) is: \[ \bar x=\dfrac{M_x}{M} \qquad \text{and} \qquad \bar y=\dfrac{M_y}{M} \] where \(M\) is the mass and the moments of the mass are: \[ M_x=\iint_R x\,\delta\,dA=\iint_R x\,\delta\,J\,du\,dv \] and \[ M_y=\iint_R y\,\delta\,dA=\iint_R y\,\delta\,J\,du\,d \]

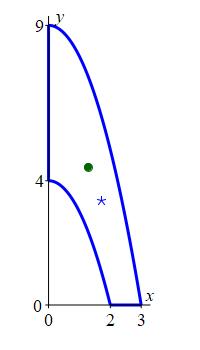
Find the center of mass of the region between the parabolas if the mass density is \(\delta=x\).

We already know the mass is \[ M=\iint_R \delta\,dA=\dfrac{65}{4}\approx16.24 \] The \(x\)-moment of the mass is: \[\begin{aligned} M_x&=\iint_R x\delta\,dA=\iint_R x^2J\,dv\,du \\ &=\int_4^9\int_{-u}^u \dfrac{(u-v)}{2} \dfrac{1}{2\sqrt{2}\sqrt{u-v}}\,dv\,du \\ &=\dfrac{1}{4\sqrt{2}}\int_4^9\int_{-u}^u \sqrt{u-v}\,dv\,du \\ &=\dfrac{1}{4\sqrt{2}}\int_4^9\left[\dfrac{-2(u-v)^{3/2}}{3}\right]_{v=-u}^u\,du =\dfrac{1}{6\sqrt{2}}\int_4^9(2u)^{3/2}\,du \\ &=\dfrac{1}{3}\int_4^9 u^{3/2}\,du =\dfrac{1}{3}\left[\dfrac{2u^{5/2}}{5}\right]_4^9 =\dfrac{2}{15}(9^{5/2}-4^{5/2}) \\ &=\dfrac{2}{15}(3^5-2^5) =\dfrac{422}{15}\approx28.1 \end{aligned}\] The \(y\)-moment of the mass is: \[ M_y=\iint_R y\delta\,dA=\iint_R yxJ\,dv\,du \] This is the same integral as the volume computed in a previous example. Consequently: \[ M_y=\dfrac{665}{12}\approx55.4 \]

So the center of mass is: \[\begin{aligned} \bar x&=\dfrac{M_x}{M}=\dfrac{422}{15}\dfrac{4}{65} =\dfrac{1688}{975}\approx1.73 \\ \bar y&=\dfrac{M_y}{M}=\dfrac{665}{12}\dfrac{4}{65} =\dfrac{131}{39}\approx3.36 \end{aligned}\] The center of mass is plotted in the region as a blue star.

The plot shows the same region between 2 parabolas plus a star for the center of mass at x = 1.73 and y = 3.36.

Centroid

The centroid of a region \(R\) is: \[ \bar x=\dfrac{A_x}{A} \qquad \text{and} \qquad \bar y=\dfrac{A_y}{A} \] where \(A\) is the area and the moments of the area are: \[ A_x=\iint_R x\,dA=\iint_R x\,J\,du\,dv \] and \[ A_y=\iint_R y\,dA=\iint_R y\,J\,du\,d \]

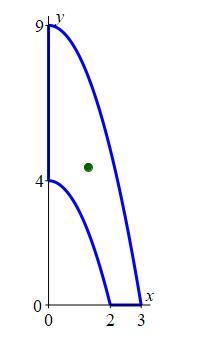
Find the centroid of the region between the parabolas.

We know the area is \[ A=\iint_R 1\,dA=\dfrac{38}{3}\approx12.7 \] The \(x\)-moment of the area is: \[ A_x=\iint_R x\,dA=\iint_R xJ\,dv\,du \] This is the same integral as the mass, computed in a previous example. Consequently: \[ A_x=\dfrac{65}{4}\approx16.24 \] The \(y\)-moment of the area is: \[\begin{aligned} A_y&=\iint_R y\,dA=\iint_R yJ\,dv\,du \\ &=\int_4^9\int_{-u}^u \dfrac{(u+v)}{2} \dfrac{1}{2\sqrt{2}\sqrt{u-v}}\,dv\,du \\ &=\dfrac{1}{4\sqrt{2}}\int_4^9\int_{-u}^u \dfrac{u+v}{\sqrt{u-v}}\,dv\,du \\ \end{aligned}\] At this point, we make the substitution \(w=u-v\) and \(dw=-dv\): \[\begin{aligned} A_y&=-\,\dfrac{1}{4\sqrt{2}}\int_4^9\int_{2u}^0 \dfrac{2u-w}{\sqrt{w}}\,dw\,du \\ &=-\,\dfrac{1}{4\sqrt{2}}\int_4^9\left[4u\sqrt{w}-\dfrac{2w^{3/2}}{3}\right]_{2u}^0\,du \\ &=\dfrac{1}{4\sqrt{2}}\int_4^9\left(4u\sqrt{2u}-\dfrac{2(2u)^{3/2}}{3}\right)\,du \\ &=\int_4^9\left(u\sqrt{u}-\dfrac{u^{3/2}}{3}\right)\,du =\dfrac{2}{3}\int_4^9 u^{3/2}\,du \\ &=\dfrac{2}{3}\left[2\dfrac{u^{5/2}}{5}\right]_4^9 =\dfrac{4}{15}\left(9^{5/2}-4^{5/2}\right) \\ &=\dfrac{4}{15}\left(3^5-2^5\right) =\dfrac{844}{15}\approx56.27 \end{aligned}\]

So the centroid is: \[\begin{aligned} \bar x&=\dfrac{A_x}{A}=\dfrac{65}{4}\dfrac{3}{38} =\dfrac{195}{152}\approx1.28 \\ \bar y&=\dfrac{A_y}{A}=\dfrac{844}{15}\dfrac{3}{38} =\dfrac{2532}{570}=4.44 \end{aligned}\] The centroid is plotted in the region as a green circle.

The plot shows the same region between 2 parabolas plus a circle for the centroid at x = 1.28 and y = 4.44.

Since the density \(\delta=x\) increases with \(x\), and the bottom of the shape has larger values of \(x\), we expect the center of mass to be to the right and below the centroid which it is.

The center of mass is plotted in the region as a blue star.

The centroid is plotted in the region as a green circle.

The plot shows the same region between 2 parabolas plus a star for the center of mass at x = 1.73 and y = 3.36 and a circle for the centroid at x = 1.28 and y = 4.44. The center of mass is to the right and below the centroid.

Average Value

The average value of a function \(f(x,y)\) on a region \(R\) is: \[ f_\text{ave}=\dfrac{1}{A}\iint_R f(x,y)\,dA =\dfrac{1}{A}\iint_R f(u,v)\,J\,du\,dv \] where \(A\) is the area.

Find the average value of the function \(f(x,y)=x^3\) on the region between the parabolas.

The average value of the of the function is \[ f_\text{ave}=\dfrac{1}{A}\iint f\,dA \] We know the area is \(A=\dfrac{38}{3}\). We compute: \[\begin{aligned} \iint &f\,dA=\iint x^3\,J\,dv\,du \\ &=\int_4^9\int_{-u}^u \dfrac{(u-v)^{3/2}}{2^{3/2}} \dfrac{1}{2\sqrt{2}\sqrt{u-v}}\,dv\,du \\ &=\dfrac{1}{8}\int_4^9\int_{-u}^u (u-v)\,dv\,du \\ &=\dfrac{1}{8}\int_4^9\left[uv-\dfrac{v^2}{2}\right]_{-u}^u\,du \\ &=\dfrac{1}{8}\int_4^9\left[\left(u^2-\dfrac{u^2}{2}\right) -\left(-u^2-\dfrac{(-u)^2}{2}\right)\right]\,du \\ &=\dfrac{1}{8}\int_4^9\left(2u^2\right)\,du =\dfrac{1}{4}\left[\dfrac{u^3}{3}\right]_4^9 \\ &=\dfrac{1}{12}\left(9^3-4^3\right) =\dfrac{665}{12} \end{aligned}\] So the average value is: \[ f_\text{ave}=\dfrac{3}{38}\dfrac{665}{12}=\dfrac{35}{8}=4.375 \]

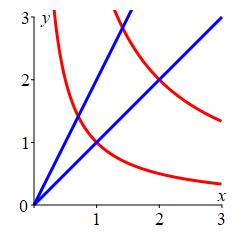
The exercises on the rest of this page refer to the diamond shaped region discusssed in the last exercise on the previous page. The boundaries are the curves \(y=\dfrac{1}{x}\) and \(y=\dfrac{4}{x}\) in red and \(y=x\) and \(y=2x\) in blue. We already know:
 The coordinates may be taken as \(u=xy\) and \(v=\dfrac{y}{x}\).
 Then the boundaries are \(u=1\), \(u=4\), \(v=1\) and \(v=2\).
 The coordinate system is \(x=\sqrt{\dfrac{u}{v}}\) and \(y=\sqrt{uv}\).
 The Jacobian factor is \(J=\dfrac{1}{2v}\).
 And the area is \(\dfrac{3}{2}\ln2\).

The plot shows two lines through the origin with slopes 1 and 2. It also shows two hyperbolas y = 1 over x and y = 4 over x.

Find the volume of the solid above the diamond below the surface \(z=y^2\).

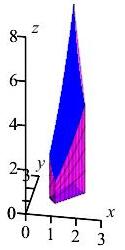
The plot shows a solid above the diamond. It has vertical sides and a top which slopes down toward the origin.

The volume is \(\displaystyle V=\iint_R y^2 J\,du\,dv\).

\(\displaystyle V=\dfrac{15}{4}\)

The volume is \[ V=\iint y^2 J\,du\,dv \] We already know the bounds on \(u\) and \(v\) are: \[ 1 \le u \le 4 \quad \text{and} \quad 1 \le v \le 2 \] And the Jacobian is: \[ J=\dfrac{1}{2v} \] The last thing we need is the integrand: \[ y^2=(\sqrt{uv})^2=uv \] We can now compute the volume: \[\begin{aligned} V&=\int_1^2\int_1^4 uv\dfrac{1}{2v}\,du\,dv =\dfrac{1}{2}\int_1^2\int_1^4 u\,du\,dv \\ &=\dfrac{1}{2}\left[\dfrac{u^2}{2}\right]_1^4\left[\rule{0pt}{10pt}v\right]_1^2 =\dfrac{1}{2}\left(\dfrac{16-1}{2}\right)(2-1) =\dfrac{15}{4} \end{aligned}\]

Find the mass of the diamond shaped region if the mass density is \(\delta=\dfrac{xy}{2}\).

The mass is \(\displaystyle M=\iint_R \delta\,J\,du\,dv\).

\(\displaystyle M=\dfrac{15}{8}\ln2\approx1.30\)

Since \(x=\sqrt{\dfrac{u}{v}}\) and \(y=\sqrt{uv}\) the density is: \[ \delta=\dfrac{xy}{2}=\dfrac{1}{2}\sqrt{\dfrac{u}{v}}\sqrt{uv}=\dfrac{u}{2} \] So the mass of the region is given by \[\begin{aligned} M&=\iint\limits_R \delta\,dA =\int_1^2\int_1^4 \dfrac{u}{2}\left(\dfrac{1}{2v}\right)\,du\,dv \\ &=\dfrac{1}{4}\int_1^4 u\,du\int_1^2 \dfrac{1}{v}\,dv =\dfrac{1}{4}\left[\dfrac{u^2}{2}\right]_1^4\left[\ln|v|\right]_1^2 \\ &=\dfrac{15}{8}\ln2 \approx1.30 \end{aligned}\]

Find the center of mass of the diamond shaped region if the mass density is \(\delta=\dfrac{xy}{2}\).

The moments of the mass are: \[ M_x=\iint_R x\,\delta\,J\,du\,dv \quad \text{and} \quad M_y=\iint_R y\,\delta\,J\,du\,dv \]

The center of mass is
\(\begin{aligned} \bar{x}&\approx1.40\rule{0pt}{12pt} \\ \bar{y}&\approx1.98 \end{aligned}\)

Since \(x=\sqrt{\dfrac{u}{v}}\), \(y=\sqrt{uv}\) and the mass density is \(\delta=\dfrac{u}{2}\), then the moments of mass are \[\begin{aligned} M_x&=\iint\limits_R x\,\delta\,J\,du\,dv =\int_1^2\int_1^4 \sqrt{\dfrac{u}{v}}\dfrac{u}{2}\dfrac{1}{2v}\,du\,dv \\ &=\dfrac{1}{4}\int_1^4 u^{3/2}\,du\int_1^2 v^{-3/2}\,dv =\dfrac{1}{4}\left[\dfrac{2u^{5/2}}{5}\right]_1^4\left[-2v^{-1/2}\right]_1^2 \\ &=\dfrac{1}{4}\cdot\dfrac{2}{5}\left(32-1\right)\left(\dfrac{-2}{\sqrt{2}}+2\right) =\dfrac{31}{10}\left(2-\sqrt{2}\right) \approx1.82 \end{aligned}\] and \[\begin{aligned} M_y&=\iint\limits_R y\,\delta\,J\,du\,dv =\int_1^2\int_1^4 \sqrt{uv}\dfrac{u}{2}\dfrac{1}{2v}\,du\,dv \\ &=\dfrac{1}{4}\int_1^4 u^{3/2}\,du\int_1^2 v^{-1/2}\,dv =\dfrac{1}{4}\left[\dfrac{2u^{5/2}}{5}\right]_1^4\left[2v^{1/2}\right]_1^2 \\ &=\dfrac{1}{4}\cdot\dfrac{2}{5}\left(32-1\right)\left(2\sqrt{2}-2\right) =\dfrac{31}{5}(\sqrt{2}-1) \approx2.57 \end{aligned}\]

Thus the center of mass for this region and given density is \[\begin{aligned} \bar{x}&=\dfrac{M_x}{M}\approx\dfrac{1.82}{1.30}=1.40 \\[5pt] \bar{y}&=\dfrac{M_y}{M}\approx\dfrac{2.57}{1.30}=1.98 \end{aligned}\] The center of mass is plotted in the region as a blue star.

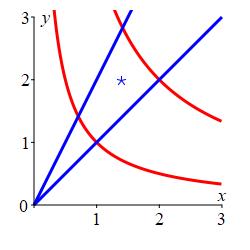
The plot shows the same region with 2 radial lines and 2 hyperbolas plus a star for the center of mass at x = 1.40 and y = 1.98,

Find the centroid of the diamond shaped region.

The moments of the area are: \[ A_x=\iint_R x\,J\,du\,dv \quad \text{and} \quad A_y=\iint_R y\,J\,du\,dv \]

The centroid is:
\(\begin{aligned} \bar{x}&\approx1.31\rule{0pt}{12pt} \\ \bar{y}&\approx=1.86 \end{aligned}\)

We know the area is: \(\dfrac{3}{2}\ln2\). \[ A=\dfrac{3}{2}\ln2\approx1.04 \] We again calculate the moments in \(x\) and \(y\) directions, but this time the density function is \(\delta=1\). So we are calculating the moments of area: \[\begin{aligned} A_x&=\iint\limits_R x\,J\,du\,dv =\int_1^2\int_1^4 \sqrt{\dfrac{u}{v}}\dfrac{1}{2v}\,du\,dv \\ &=\dfrac{1}{2}\int_1^4 u^{1/2}\,du\int_1^2 v^{-3/2}\,dv =\dfrac{1}{2}\left[\dfrac{2u^{3/2}}{3}\right]_1^4\left[-2v^{-1/2}\right]_1^2 \\ &=\dfrac{1}{2}\cdot\dfrac{2}{3}\left(8-1\right)\left(\dfrac{-2}{\sqrt{2}}+2\right) =\dfrac{7}{3}\left(2-\sqrt{2}\right) \approx1.37 \end{aligned}\] and \[\begin{aligned} A_y&=\iint\limits_R y\,J\,du\,dv =\int_1^2\int_1^4 \sqrt{uv}\dfrac{1}{2v}\,du\,dv \\ &=\dfrac{1}{2}\int_1^4 u^{1/2}\,du\int_1^2 v^{-1/2}\,dv =\dfrac{1}{2}\left[\dfrac{2u^{3/2}}{3}\right]_1^4\left[2v^{1/2}\right]_1^2 \\ &=\dfrac{1}{2}\cdot\dfrac{2}{3}\left(8-1\right)\left(2\sqrt{2}-2\right) =\dfrac{14}{3}(\sqrt{2}-1) \approx1.93 \end{aligned}\]

Thus the centroid for this region is \[\begin{aligned} \bar{x}&=\dfrac{A_x}{A}\approx\dfrac{1.37}{1.04}=1.31 \\ \bar{y}&=\dfrac{A_y}{A}\approx\dfrac{1.93}{1.04}=1.86 \end{aligned}\] The centroid is plotted in the region as a green circle.

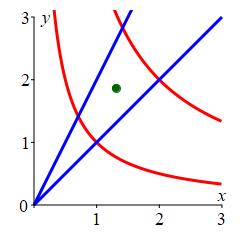
The plot shows the same region with 2 radial lines and 2 hyperbolas plus a circle for the centroid at x = 1.31 and y = 1.86.

Since the density \(\delta=\dfrac{xy}{2}\) increases with \(x\) and \(y\), we expect the center of mass to be to the right and up from the centroid which it is.

The center of mass is plotted in the region as a blue star.

The centroid is plotted in the region as a green circle.

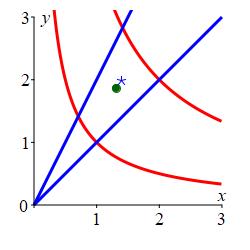
The plot shows the same region with 2 radial lines and 2 hyperbolas plus a star for the center of mass at x = 1.40 and y = 1.98, and a circle for the centroid at x = 1.31 and y = 1.86. The center of mass is a little to the right and above the centroid.

Find the average density of the diamond region if the density is \(\delta=\dfrac{xy}{2}\).

There are two formulas for the average density, but they are equal: \[ \delta_\text{ave}=\dfrac{1}{A}\iint_R \delta\,dA =\dfrac{M}{A} \] since the integral of the density is the mass.

\(\displaystyle \delta_\text{ave}=\dfrac{5}{4}\)

The average density is simply the total mass divided by the area of the region, both of which we have already calculated: \[ \delta_\text{ave}=\dfrac{M}{A} =\dfrac{15\ln2}{8}\dfrac{2}{3\ln2} =\dfrac{5}{4} \]

© MYMathApps

Supported in part by NSF Grant #1123255