21. Multiple Integrals in Curvilinear Coordinates
a. Integrating in Polar Coordinates
1. Grid Cells
In the previous chapter, you learned how to integrate in rectangular coodinates in 2 and 3 dimensions. You will now learn how to integrate in polar, cylindrical, spherical and other curvilinear coordinate systems.
In the Riemann sum definition of a double integral, we break up the region of integration \(R\) into \(n\) subregions \(R_k\) for \(k=1,2,\ldots,n\) in such a way that you know (or can approximate) the area \(\Delta A_k\) of the \(k^\text{th}\) subregion \(R_k\). When integrating in rectangular coordinates, the subregions are small rectangles whose areas are \(\Delta A=\Delta x\Delta y\). In the limit as \(\Delta x\) and \(\Delta y\) get small, we write the rectangular differential of area as \(dA=dx\,dy\). To integrate in polar coordinates, the subregions are polar rectangles and we need to know the area of these cells.
A polar rectangle or polar grid cell is a region of the form: \[ r_1 \le r \le r_2 \qquad \text{and} \qquad \theta_1 \le \theta \le \theta_2 \] See the figure at the right. The coordinate center of the cell is at: \[ \bar{r}=\dfrac{r_1+r_2}{2} \qquad \text{and} \qquad \bar{\theta}=\dfrac{\theta_1+\theta_2}{2} \] and the coordinate dimensions of the cell are: \[ \Delta r=r_2-r_1 \qquad \text{and} \qquad \Delta\theta=\theta_2-\theta_1 \]
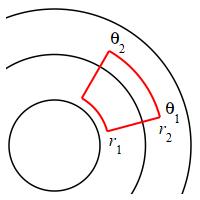
At first thought, you might guess the area of the grid cell is
WRONG! \( \Delta A=\Delta r\Delta\theta \) WRONG!
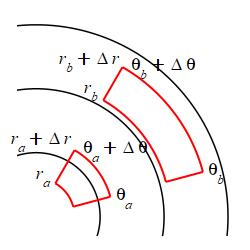
However, this can't be correct because the area must get bigger as \(r\) gets bigger even when \(\Delta r\) and \(\Delta\theta\) stay the same. See the figure at the right.
Further, \(\Delta A\) must have units of area but \(\Delta r\Delta\theta\) has units of length times angle.
Intuitively, the length is \(\Delta r\) (which stays the same from box to box), and the width is \(\bar r \Delta \theta\) (which gets bigger as the box moves away from the origin).
The correct area is found as follows:
First note that the area of the ring between radii \(r_1\) and \(r_2\) is:
\[
A_\circledcirc=\pi\,(r_2)^2-\pi\,(r_1)^2
=\pi\,(r_1+r_2)(r_2-r_1)
\]
Further, the fraction of this ring within the grid cell is
\(\dfrac{\Delta\theta}{2\pi}\) where \(\Delta\theta\) is in radians.
So the area in the cell is
\[\begin{aligned}
\Delta A&=\dfrac{\Delta\theta}{2\pi}A_\circledcirc
=\dfrac{\Delta\theta}{2\pi}\pi\,(r_1+r_2)(r_2-r_1) \\
&=\left(\dfrac{r_1+r_2}{2}\right)(r_2-r_1)\Delta\theta
\end{aligned}\]
Since \(\dfrac{r_1+r_2}{2}=\bar{r}\) and \(r_2-r_1=\Delta r\), we conclude:
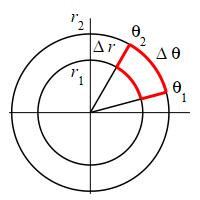
The area of a polar rectangle is: \[ \Delta A=\bar{r}\Delta r\Delta\theta \]
In the limit as \(\Delta r\) and \(\Delta\theta\) get small, \(\Delta r\) becomes \(dr\), \(\Delta\theta\) becomes \(d\theta\) and \(\Delta A\) becomes \(dA\). Consequently:
The polar differential of area is: \[ dA=r\,dr\,d\theta \]
Memorize this!
We will see how the differential of area is used in integrals on the next page.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum