21. Multiple Integrals in Curvilinear Coordinates
b. Integrating in Cylindrical Coordinates
2. Integral over a Cylindrical Region
We now explore integration in cylindrical coordinates with constant and non-constant limits.
Integral over a Cylindrical Box
We first want to integrate over the cylindrical box \[ r_1 \le r \le r_2 \qquad \theta_1 \le \theta \le \theta_2 \qquad z_1 \le z \le z_2 \] Using the Riemann Sum definition with \(\Delta V_{ijk}=r_i^*\,\Delta r_i\,\Delta\theta_j\,\Delta z_k\), the integral is: \[ \iiint_R f(r,\theta,z)\,dV =\lim_{p\rightarrow\infty} \lim_{q\rightarrow\infty} \lim_{s\rightarrow\infty} \sum_{i=1}^p\sum_{j=1}^q\sum_{k=1}^s f(r_i^*,\theta_j^*,z_k^*)\,r_i^*\Delta r_i\Delta\theta_j\Delta z_k \] We recognize this as the triple iterated integral: \[ \iiint\limits_R f(r,\theta,z)\,dV =\int_{z_1}^{z_2}\int_{\theta_1}^{\theta_2}\int_{r_1}^{r_2} f(r,\theta,z)\,r\,dr\,d\theta\,dz \] By Fubini's Theorem, there are five other orders of integrations obtained by reordering the limits, sums and differentials.
Other Integrals in Cylindrical Coordinates
In addition to integrating over cylindrical boxes, cylindrical coordinates can be used to integrate over other types of regions with appropriate definitions of the regions. The resulting integrals have the forms:
Type \(r\theta\): \[ \iiint\limits_R f(r,\theta,z)\,dV =\int_{r_1}^{r_2}\int_{g(r)}^{h(r)}\int_{p(r,\theta)}^{q(r,\theta)} f(r,\theta,z)\,r\,dz\,d\theta\,dr \] Type \(\theta r\): \[ \iiint\limits_R f(r,\theta,z)\,dV =\int_{\theta_1}^{\theta_2}\int_{g(\theta)}^{h(\theta)} \int_{p(r,\theta)}^{q(r,\theta)} f(r,\theta,z)\,r\,dz\,dr\,d\theta \] Type \(rz\): \[ \iiint\limits_R f(r,\theta,z)\,dV =\int_{r_1}^{r_2}\int_{g(r)}^{h(r)}\int_{p(r,z)}^{q(r,z)} f(r,\theta,z)\,r\,d\theta\,dz\,dr \] Type \(zr\): \[ \iiint\limits_R f(r,\theta,z)\,dV =\int_{z_1}^{z_2}\int_{g(z)}^{h(z)}\int_{p(r,z)}^{q(r,z)} f(r,\theta,z)\,r\,d\theta\,dr\,dz \] Type \(\theta z\): \[ \iiint\limits_R f(r,\theta,z)\,dV =\int_{\theta_1}^{\theta_2}\int_{g(\theta)}^{h(\theta)} \int_{p(\theta,z)}^{q(\theta,z)} f(r,\theta,z)\,r\,dr\,dz\,d\theta \] Type \(z\theta\): \[ \iiint\limits_R f(r,\theta,z)\,dV =\int_{z_1}^{z_2}\int_{g(z)}^{h(z)}\int_{p(\theta,z)}^{q(\theta,z)} f(r,\theta,z)\,r\,dr\,d\theta\,dz \]
Notice that each integral can have limits which depend only on the variables outside that integral.
The top surface of this spiral ramp is given in cylindrical coordinates by
\(z=\theta\) independent of \(r\). Its radius is \(r=2\). The ramp will
be 3D printed with a density \(\delta=2(\theta-z)\). (The point on the
ramp directly above the point \((r,\theta,z)\) is \((r,\theta,\theta)\).
So this density says that at each point the density is proportional to the
distance up to the ramp directly above that point.) Find the total mass
of the spiral ramp. (Rotate the plot with your mouse.)

The volume of the spiral ramp could be computed using the triple integral \(\displaystyle V=\int_0^2\int_0^{2\pi}\int_0^\theta 1\,r\,dz\,d\theta\,dr\) or using the double integral \(\displaystyle V=\int_0^2\int_0^{2\pi} \theta\,r\,d\theta\,dr\), but the mass must be computed using a triple integral.
The mass is given by \[\begin{aligned} M&=\iiint \delta\,dV =\int_0^2\int_0^{2\pi}\int_0^\theta 2(\theta-z)\,r\,dz\,d\theta\,dr \\ &=\int_0^2 2r\,dr\int_0^{2\pi}\int_0^\theta (\theta-z)\,dz\,d\theta \\ &=\left[r^2\dfrac{}{}\right]_0^2\int_0^{2\pi} \left[\theta z-\,\dfrac{z^2}{2}\right]_0^\theta\,d\theta \\ &=4\int_0^{2\pi} \dfrac{\theta^2}{2}\,d\theta =4\left[\dfrac{\theta^3}{6}\right]_0^{2\pi} =4\dfrac{(2\pi)^3}{6} =\dfrac{16}{3}\pi^3 \end{aligned}\]
Find the volume of the spiral ramp in the previous example.
\(V=4\pi^2\)
The volume is given by \[\begin{aligned} V&=\int_0^2\int_0^{2\pi} \theta\,r\,d\theta\,dr \\ &=\int_0^2 r\,dr\int_0^{2\pi} \theta\,d\theta =\left[\dfrac{r^2}{2}\right]_0^2\left[\dfrac{\theta^2}{2}\right]_0^{2\pi} \\ &=2\dfrac{(2\pi)^2}{2} =4\pi^2 \end{aligned}\]
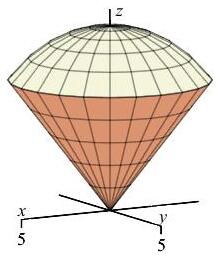
Use cylindrical coordinates to find the mass of the ice cream cone between the cone \(z=\sqrt{x^2+y^2}\) and the hemisphere \(z=\sqrt{50-x^2-y^2}\) if the mass density is \(\delta=z(x^2+y^2)\).
\(M=\dfrac{5^6}{6}\pi\)
Computing the mass of a region requires integration of the density function over the region: \[ M=\iiint \delta\,dV=\iiint z(x^2+y^2)\,dV \] First, we express the integrand and volume element \(dV\) in cylindrical coordinates: \[ M=\iiint \,z(r^2)\,r\,dr\,d\theta\,dz=\iiint zr^3\,dr\,d\theta\,dz \] Next, we consider the bounds on the integral. The given equations for the hemisphere and cone can be expressed as functions of \(r\) in cylindrical coordinates: \[\begin{aligned} z&=\sqrt{x^2+y^2}=r \\ z&=\sqrt{50-x^2-y^2}=\sqrt{50-r^2} \end{aligned}\] Equating these, we find the intersection of the two: \[ r=\sqrt{50-r^2} \quad \Rightarrow \quad 2r^2=50 \quad \Rightarrow \quad r=5 \] The \(\theta\) parameter goes all \(2\pi\) around and the \(z\) bounds are from the cone to the hemisphere. Thus the bounds are \[ 0 \le r \le5 \qquad 0 \le \theta \le 2\pi \qquad r \le z \le \sqrt{50-r^2} \] The bounds on \(z\) are the only non-constant bounds, so they go on the inside and the integral is set up and computed as \[\begin{aligned} M&=\int_0^{2\pi}\int_0^5\int_r^{\sqrt{50-r^2}} zr^3\,dz\,dr\,d\theta =\int_0^{2\pi} \,d\theta\int_0^5 \left[\dfrac{z^2}{2}r^3\right]_{z=r}^{\sqrt{50-r^2}}\,dr \\ &=\pi\int_0^5 ((50-r^2)r^3-r^5)\,dr =\pi\int_0^5 (50r^3-2r^5)\,dr \\ &=\pi\left[\dfrac{25r^4}{2}-\,\dfrac{r^6}{3}\right]_0^5 =\pi\left(\dfrac{25(5^4)}{2}-\,\dfrac{5^6}{3}\right) =\dfrac{5^6}{6}\pi \end{aligned}\]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum