21. Multiple Integrals in Curvilinear Coordinates
e. Integrating in 3D Curvilinear Coordinates
2. Grid Cell Volume
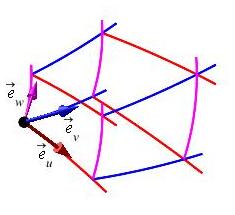
We continue our investigation of how to integrate in general 3D curvilinear coordinate systems. We continue to use spherical coordinates as a concrete example. Once again, here are the spherical coordinate grid and the general curvilinear coordinate grid with a tangent vector to each coordinate curve:
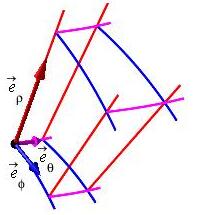
To integrate in spherical coordinates, we need to know (or be able to approximate) the volume of each curvilinear box (or grid cell): \[ \rho_0 \le \rho \le \rho_0+\Delta\rho \qquad \theta_0 \le \theta \le \theta_0+\Delta\theta \qquad \phi_0 \le \phi \le \phi_0+\Delta\phi \] Again, we are moving toward showing the differential of volume is \(dV=\rho^2\sin\phi\,d\rho\,d\theta\,d\phi\).
To integrate in 3D curvilinear coordinates, we need to know (or be able to approximate) the volume of each curvilinear box or grid cell: \[ u_0 \le u \le u_0+\Delta u\qquad v_0 \le v \le v_0+\Delta v\qquad w_0 \le w \le w_0+\Delta w \] It turns out that this volume is \[ \Delta V=J\,\Delta u\,\Delta v\,\Delta w \] where \(J\) is a function, called the Jacobian factor, which differs from one coordinate system to another. Then the differential of volume will be: \[ dV=J\,du\,dv\,dw \] From this the integral \(\displaystyle \iiint_R f\,dV\) can be computed as \[ \iiint_R f\,dV=\iiint f(u,v,w)\,J\,du\,dv\,dw \] where the limits are put on the integrals to describe the region \(R\).
For 3D rectangular coordinates, \(dV=dx\,dy\,dz\). So \(J=1\).
For cylindrical coordinates, \(dV=r\,dr\,d\theta\,dz\). So \(J=r\).
For spherical coordinates, we will show
\(dV=\rho^2\sin\phi\,d\rho\,d\theta\,d\phi\). So \(J=\rho^2\sin\phi\).
Our job is to find \(J\) for other coordinate systems.
Volume of a Coordinate Box or Grid Cell
We need to compute (or approximate) the volume of the curvilinear box or grid cell: \[ u_0 \le u \le u_0+\Delta u\qquad v_0 \le v \le v_0+\Delta v\qquad w_0 \le w \le w_0+\Delta w \] To do this, we stretch (or shrink) the tangent vectors \(\vec{e}_u\), \(\vec{e}_v\) and \(\vec{e}_w\) to vectors \(\vec{U}\), \(\vec{V}\) and \(\vec{W}\), respectively, which just touch the next coordinate curve, and approximate the volume of the coordinate box by the volume of the parallelepiped with edges \(\vec{U}\), \(\vec{V}\) and \(\vec{W}\). These vectors and the parallelepiped are added to the plots below:
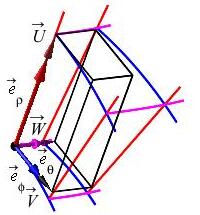
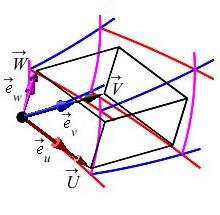
As with 2D curvilinear coordinates, the vector \(\vec{U}\) is constructed so that \(\vec{U}\) points in the same direction as \(\vec{e}_u\): \[ \hat{U}=\hat{e}_u=\dfrac{\vec{e}_u}{|\vec{e}_u|} \] and the length of \(\vec{U}\) is the arclength of the \(u\)-curve from \(u=u_0\) to \(u=u_0+\Delta u\): \[ |\vec{U}|=\int_{u_0}^{u_0+\Delta u} |\vec{e}_u|\,du\approx|\vec{e}_u|\,\Delta u \] From the magnitude and direction of \(\vec{U}\), we reconstruct \(\vec{U}\): \[ \vec{U}=|\vec{U}|\hat{U}\approx\Delta u\,\vec{e}_u \] Similarly \[ \vec{V}\approx\Delta v\,\vec{e}_v \qquad \text{and} \qquad \vec{W}\approx\Delta w\,\vec{e}_w \] The volume of the coordinate box, \(\Delta V\), is approximately the volume of the parallelepiped which is the absolute value of the triple product, \(|\vec{U}\times\vec{V}\cdot\vec{W}|\). (See the applications of the cross product.) So: \[ \Delta V=|\vec{U}\times\vec{V}\cdot\vec{W}| =|\Delta u\,\vec{e}_u\times\Delta v\,\vec{e}_v\cdot\Delta w\,\vec{e}_w| =|\vec{e}_u\times\vec{e}_v\cdot\vec{e}_w|\,\Delta u\,\Delta v\,\Delta w \] In the limit as \(\Delta u\), \(\Delta v\) and \(\Delta w\) get small, all the approximations go away and the differential of volume becomes \[ dV=|\vec{e}_u\times\vec{e}_v\cdot\vec{e}_w|\,du\,dv\,dw \] Comparing this to the formula \[ dV=J\,du\,dv\,dw \] from the top of this page, we see that the Jacobian factor is \[J=|\vec{e}_u\times\vec{e}_v\cdot\vec{e}_w|\]
The Jacobian factor will be simplified on the next page, but this is the basic requirement for integrating in general curvilinear coordinates on the page after next.
The Jacobian for spherical coordinates will be calculated at the end of the next page
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum