1. Coordinate Systems

Exercises

    a. Rectangular Coordinates - 2D, 3D and nD

  1. Find the rectangular coordinates of each point in \(\mathbb{R}^2\) shown in the plot:

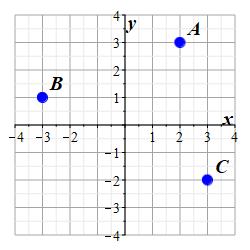
    The plot shows a point A above x = 2 and to the right of y = 3. It also has a point B above x = -3 and to the left of y = 1. It also has a point C below x = 3 and to the right of y = -2.

    1. \(A\)

      \(A=(2,3)\)

      The point \(A\) is \(2\) units to the right and \(3\) units up, or \(A=(2,3)\).

    2. \(B\)

      \(B=(-3,1)\)

      The point \(B\) is \(3\) units to the left and \(1\) unit up, or \(B=(-3,1)\).

    3. \(C\)

      \(C=(3,-2)\)

      The point \(C\) is \(3\) units to the right and \(2\) units down, or \(C=(3,-2)\).

  2. Find the rectangular coordinates of each point in \(\mathbb{R}^3\) shown in the plot:

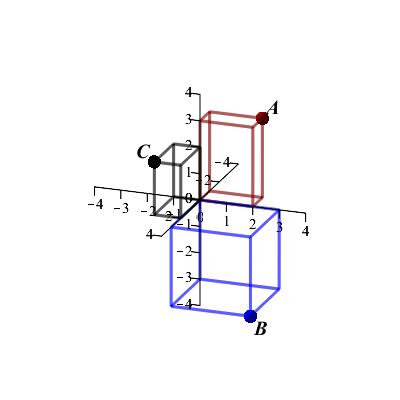
    The 3D plot shows coordinate axes with x positive in front, y positive to the right and z positive upward. There are three boxes with one vertex at the origin. The The first has its opposite vertex A at 1 behind, 2 right and 3 up. The second has its opposite vertex B at 3 in front, 3 right and 3 down. The third has its opposite vertex C at 2 in front, 1 left and 2 up.

    1. \(A\)

      \(A=(-1,2,3)\)

      The point \(A\) is \(1\) unit back, \(2\) units to the right and \(3\) units up or \(A=(-1,2,3)\).

    2. \(B\)

      \(B=(3,3,-3)\)

      The point \(B\) is \(3\) units forward, \(3\) units to the right and \(3\) units down or \(B=(3,3,-3)\).

    3. \(C\)

      \(C=(2,-1,2)\)

      The point \(C\) is \(2\) units forward, \(1\) unit to the left and \(2\) units up or \(C=(2,-1,2)\)

    3. b. Distance Formula - 2D, 3D and nD

  3. Find the distance between the following pairs of points in \(\mathbb{R}^2\):

    1. \(A=(4,1)\) and \(B=(1,5)\).

      \(d(A,B)=5\)

      \(d(A,B)=\sqrt{(4-1)^2+(1-5)^2}=\sqrt{25}=5\)

    2. \(C=(-2,5)\) and \(D=(3,-7)\).

      \(d(C,D)=13\)

      \(d(C,D)=\sqrt{(-2-3)^2+(5--7)^2}=\sqrt{25+144}=13\)

    3. \(E=(7,2)\) and \(F=(-1,8)\).

      \(d(E,F)=10\)

      \(d(E,F)=\sqrt{(7--1)^2+(2-8)^2}=\sqrt{64+36}=10\)

  4. Find the equation of a circle with each center and radius:

    1. center: \(P=(1,2)\) and radius: \(r=3\).

      \((x-1)^2+(y-2)^2=9\)

    2. center: \(P=(4,-5)\) and radius: \(r=2\).

      \((x-4)^2+(y+5)^2=4\)

  5. Find the center and radius of the circle with the given equation:

    1. \((x+4)^2+(y-3)^2=25\)

      center: \(P=(-4,3)\) and radius: \(r=5\).

    2. \((x-1)^2+(y-2)^2=3\)

      Dont't forget that in the equation \((x-a)^2+(y-b)^2=r^2\) the radius is squared on the right.

      center: \(P=(1,2)\) and radius: \(r=\sqrt{3}\).

    3. \(x^2+y^2+6x-2y=6\)

      Complete the squares on \(x\) and \(y\).

      How do I complete the square?

      Start with the quantity \(Q=Ax^2+Dx\). Factor out the \(A\) to get \(Q=A\left(x^2+\dfrac{D}{A}x\right)\).

      A perfect square has the form \((x-p)^2=x^2-2px+p^2\).

      We need \(-2p=\dfrac{D}{A}\). So we take \(p=-\,\dfrac{D}{2A}\). Then \[ \left(x+\dfrac{D}{2A}\right)^2 =x^2+\dfrac{D}{A}x+\left(\dfrac{D}{2A}\right)^2 \] So we add \(\left(\dfrac{D}{2A}\right)^2\) inside the parentheses for \(Q\) and balance it outside (Be careful with the factor of \(A\) in the constant term.): \[ Q=A\left(x^2+\dfrac{D}{A}x+\left(\dfrac{D}{2A}\right)^2\right)- \dfrac{D^2}{4A}=A\left(x+\dfrac{D}{2A}\right)^2-\,\dfrac{D^2}{4A} \] Then, if appropriate, we add \(\dfrac{D^2}{4A}\) to both sides of the equation.

      Don't memorize this formula!   Memorize the process.

      center: \(P=(-3,1)\) and radius: \(r=4\).

      We complete the squares on \(x\) and \(y\). \[\begin{aligned} x^2+6x+y^2-2y&=6 \\ (x^2+6x+9)+(y^2-2y+1)&=6+9+1 \\ (x+3)^2+(y-1)^2&=16 \end{aligned}\] So the center is \(P=(-3,1)\) and the radius is \(r=4\).

    4. \(x^2+y^2-6x+2y=-16\)

      Complete the squares on \(x\) and \(y\).

      This is not a circle. For the reason why not, read the solution.

      We complete the squares on \(x\) and \(y\). \[\begin{aligned} x^2-6x+y^2+2y&=-16 \\ (x^2-6x+9)+(y^2+2y+1)&=-16+9+1 \\ (x+3)^2+(y-1)^2&=-6 \end{aligned}\] This is not a circle because it is impossible to have the positive quantity of the left equal to the negative quantity on the right.

    5. \(x^2+y^2-4x+3y=0\)

      Complete the squares on \(x\) and \(y\).

      center: \(P=\left(2,-\,\dfrac{3}{2}\right)\) and radius: \(r=\dfrac{5}{2}\).

      We complete the squares on \(x\) and \(y\). \[\begin{aligned} x^2-4x+y^2+3y&=0 \\ (x^2-4x+4)+\left(y^2+3y+\dfrac{9}{4}\right)&=4+\dfrac{9}{4} \\ (x-2)^2+\left(y+\dfrac{3}{2}\right)^2&=\dfrac{25}{4} \end{aligned}\] So the center is \(P=\left(2,-\,\dfrac{3}{2}\right)\) and the radius is \(r=\dfrac{5}{2}\).

  6. Find the equation of the circle which satisfies the given conditions:

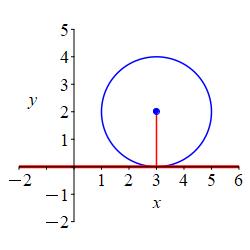
    1. The center is \(P=(3,2)\) and it is tangent to the \(x\)-axis.

      Look at a plot to figure out the radius.

      \((x-3)^2+(y-2)^2=4\)

      From the plot, we see the radius is the distance from the center to the \(x\)-axis which is \(r=2\). So the circle is: \[(x-3)^2+(y-2)^2=4\]

      The plot shows a circle centered on 3,2 which is tangent to the x-axis at x = 3.

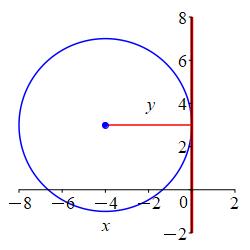
    2. The center is \(P=(-4,3)\) and it is tangent to the \(y\)-axis.

      Look at a plot to figure out the radius.

      \((x+4)^2+(y-3)^2=16\)

      From the plot, we see the radius is the distance from the center to the \(y\)-axis which is \(r=4\). So the circle is: \[(x+4)^2+(y-3)^2=16\]

      The plot shows a circle centered at -4,3 that is tangent to the y-axis at y = 3.

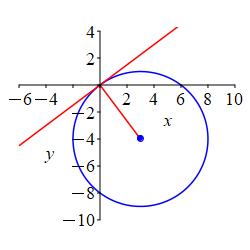
    3. The center is \(P=(3,-4)\) and it passes through the origin.

      The radius is the distance from the center to the origin.

      \((x-3)^2+(y+4)^2=25\)

      The radius is the distance from the center to the origin: \[ r=\sqrt{3^2+4^2}=5 \] So the circle is: \[ (x-3)^2+(y+4)^2=25 \]

      The plot shows a circle centered at 3,-4 which passes through the origin. It also shows the radial line from the origin to 3,-4.

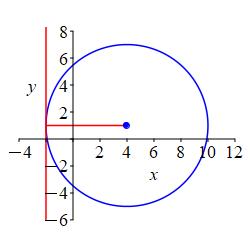
    4. The center is \(P=(4,1)\) and it is tangent to the line \(x=-2\).

      Look at a plot to figure out the radius.

      \((x-4)^2+(y-1)^2=36\)

      From the plot, we see the radius is the distance from the center to the line \(x=-2\) which is \(r=4--2=6\). So the circle is: \[(x-4)^2+(y-1)^2=36\]

      The plot shows a circle centered at 4,1 which is tangent to the line x=-2 at y = 1.

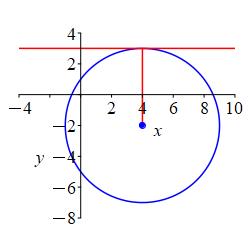
    5. The center is \(P=(4,-2)\) and it is tangent to the line \(y=3\).

      Look at a plot to figure out the radius.

      \((x-4)^2+(y+2)^2=25\)

      From the plot, we see the radius is the distance from the center to the line \(y=3\) which is \(r=3--2=5\). So the circle is: \[(x-4)^2+(y+2)^2=25\]

      The plot shows a circle centered at 4,-2 which is tangent to the line y=3 at x = 4.

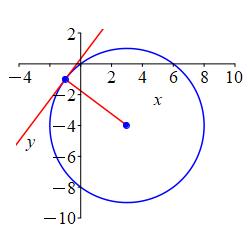
    6. The center is \(P=(3,-4)\) and it passes through the \(Q=(-1,-1)\).

      The radius is the distance from the center to \(Q=(-1,-1)\).

      \((x-3)^2+(y+4)^2=25\)

      The radius is the distance from the center to \(Q=(-1,-1)\): \[ r=\sqrt{(3--1)^2+(-4--1)^2}=5 \] So the circle is: \[ (x-3)^2+(y+4)^2=25 \]

      The plot shows a circle centered at 3,-4 which passes through the point -1, -1. It also shows the radial line and tangent line at -1,-1.
  7. Find the midpoint of the line segment with the given endpoints:

    1. \(A=(3,4)\) and \(B=(7,-2)\).

      \(M=(5,1)\)

      \(M=\dfrac{A+B}{2}=\left(\dfrac{3+7}{2},\dfrac{4-2}{2}\right)=(5,1)\)

    2. \(P=(-1,7)\) and \(Q=(4,2)\).

      \(M=\left(\dfrac{3}{2},\dfrac{9}{2}\right)\)

      \(M=\dfrac{P+Q}{2}=\left(\dfrac{-1+4}{2},\dfrac{7+2}{2}\right) =\left(\dfrac{3}{2},\dfrac{9}{2}\right)\)

  8. Find the equation of the circle with a diameter having the given end points:

    1. \(P=(-2,7)\) and \(Q=(4,-1)\)

      The center is the midpoint. The radius is half the diameter.

      \((x-1)^2+(y-3)^2=25\)

      The center is the midpoint: \[M=\dfrac{P+Q}{2}=(1,3)\] The diameter is: \[ D=d(P,Q)=\sqrt{(4--2)^2+(-1-7)^2}=\sqrt{36+64}=10 \] So the radius is \(r=5\) and the circle is: \[ (x-1)^2+(y-3)^2=25 \]

    2. \(R=(1,2)\) and \(S=(5,6)\)

      The center is the midpoint. The radius is half the diameter.

      \((x-3)^2+(y-4)^2=8\)

      The center is the midpoint: \[M=\dfrac{R+S}{2}=(3,4)\] The diameter is: \[ D=d(P,Q)=\sqrt{(5-1)^2+(6-2)^2}=\sqrt{16+16}=4\sqrt{2} \] So the radius is \(r=2\sqrt{2}\) and the circle is: \[ (x-3)^2+(y-4)^2=8 \]

  9. Find the distance between the following pairs of points in \(\mathbb{R}^3\):

    1. \(P=(1,2,3)\) and \(Q=(5,5,15)\).

      \(d(P,Q)=13\)

      \(d(P,Q)=\sqrt{(5-1)^2+(5-2)^2+(15-3)^2}=\sqrt{16+9+144}=13\)

    2. \(R=(6,6,6)\) and \(S=(1,2,3)\).

      \(d(R,S)=5\sqrt{2}\)

      \(d(R,S)=\sqrt{(6-1)^2+(6-2)^2+(6-3)^2}=\sqrt{25+16+9}=5\sqrt{2}\)

    3. \(U=(4,2,0)\) and \(V=(2,3,-2)\).

      \(d(U,V)=3\)

      \(d(U,V)=\sqrt{(4-2)^2+(2-3)^2+(0--2)^2}=\sqrt{4+1+4}=3\)

  10. Find the equation of a sphere with each center and radius:

    1. center: \(P=(1,2,3)\) and radius: \(r=4\).

      \((x-1)^2+(y-2)^2+(z-3)^2=16\)

    2. center: \(P=(4,-5,3)\) and radius: \(r=2\).

      \((x-4)^2+(y+5)^2+(z-3)^2=4\)

  11. Find the center and radius of the sphere with the given equation:

    1. \((x+4)^2+(y-3)^2+(z-2)^2=25\)

      center: \(P=(-4,3,2)\) and radius: \(r=5\).

    2. \((x-1)^2+(y-2)^2+(z-3)^2=5\)

      Don't forget that in the equation \((x-a)^2+(y-b)^2+(z-c)^2=r^2\) the radius is squared on the right.

      center: \(P=(1,2,3)\) and radius: \(r=\sqrt{5}\).

    3. \(x^2+y^2-z^2+6x-2z=8\)

      Complete the squares on \(x\) and \(z\).

      This is not a sphere because \(z^2\) has the wrong sign.

      We complete the squares on \(x\) and \(z\). \[\begin{aligned} x^2+y^2-z^2+6x-2z&=8 \\ (x^2+6x+9)+y^2-(z^2+2z+1)&=8+9-1 \\ (x+3)^2+y^2-(z+1)^2&=16 \end{aligned}\] This is not a sphere because \((z+1)^2\) has the wrong sign.

    4. \(x^2+y^2+z^2+6y-2z=6\)

      Complete the squares on \(y\) and \(z\).

      center: \(P=(0,-3,1)\) and radius: \(r=4\).

      Complete the squares on \(y\) and \(z\). \[\begin{aligned} x^2+y^2+6y+z^2-2z&=6 \\ x^2+(y^2+6y+9)+(z^2-2z+1)&=6+9+1 \\ x^2+(y+3)^2+(z-1)^2&=16 \end{aligned}\] So the center is \(P=(0,-3,1)\) and the radius is \(r=4\).

  12. Find the equation of the sphere which satisfies the given conditions:

    1. The center is \(P=(4,3,2)\) and it is tangent to the \(xy\)-plane.

      If you drop a perpendicular from the center \((4,3,2)\) to the \(xy\)-plane it hits at the point of tangency. This point has the same \(x\) and \(y\) coordinates as the center but \(z=0\) there. It is \((4,3,0)\). What is the radius?

      \((x-4)^2+(y-3)^2+(z-2)^2=4\)

      The point of tangency is \((4,3,0)\). So the distance from the center \((4,3,2)\) is the radius \(r=2\). So the sphere is: \[(x-4)^2+(y-3)^2+(z-2)^2=4\]

    2. The center is \(P=(5,4,-3)\) and it is tangent to the \(yz\)-plane.

      If you drop a perpendicular from the center to the \(yz\)-plane, only the \(x\) coordinate changes, and it changes by the radius.

      \((x-5)^2+(y-4)^2+(z+3)^2=25\)

      The point of tangency is \((0,4,-3)\). So the radius is \(r=5\) and the sphere is: \[(x-5)^2+(y-4)^2+(z+3)^2=25\]

    3. The center is \(P=(-2,1,2)\) and it passes through the origin.

      The radius is the distance from the center to the origin.

      \((x+2)^2+(y-1)^2+(z-2)^2=9\)

      The radius is the distance from the center to the origin: \[ r=\sqrt{(-2)^2+1^2+2^2}=3 \] So the sphere is: \[ (x+2)^2+(y-1)^2+(z-2)^2=9 \]

    4. The center is \(P=(3,-4,2)\) and it is tangent to the plane \(y=3\).

      If you drop a radius from the center to the plane \(y=3\), only the \(y\) coordinate changes. What is the radius?

      \((x-3)^2+(y+4)^2+(z-2)^2=49\)

      If you drop a radius from the center to the plane \(y=3\), only the \(y\) coordinate changes and it changes from \(-4\) to \(3\). So the radius is \(r=3-(-4)=7\) and the sphere is: \[(x-3)^2+(y+4)^2+(z-2)^2=49\]

    5. The center is \(P=(-5,-1,-3)\) and it passes through the \(Q=(7,3,0)\).

      The radius is the distance from the center \(P=(-5,-1,-3)\) to \(Q=(7,3,0)\).

      \((x+5)^2+(y+1)^2+(z+3)^2=169\)

      lh~ 

      The radius is the distance from the center \(P=(-5,-1,-3)\) to \(Q=(7,3,0)\): \[ r=\sqrt{(7--5)^2+(3--1)^2+(0--3)^2}=\sqrt{144+16+9}=13 \] So the sphere is: \[ (x+5)^2+(y+1)^2+(z+3)^2=169 \]

  13. Find the midpoint of the line segment with the given endpoints:

    1. \(A=(3,4,5)\) and \(B=(7,-2,3)\).

      \(M=(5,1,4)\)

      \(M=\dfrac{A+B}{2} =\left(\dfrac{3+7}{2},\dfrac{4-2}{2},\dfrac{5+3}{2}\right)=(5,1,4)\)

    2. \(P=(-1,3,7)\) and \(Q=(4,8,2)\).

      \(M=\left(\dfrac{3}{2},\dfrac{11}{2},\dfrac{9}{2}\right)\)

      \(M=\dfrac{P+Q}{2}=\left(\dfrac{-1+4}{2},\dfrac{3+8}{2},\dfrac{7+2}{2}\right) =\left(\dfrac{3}{2},\dfrac{11}{2},\dfrac{9}{2}\right)\)

  14. Find the equation of the sphere with a diameter having the given end points:

    1. \(P=(5,-3,-2)\) and \(Q=(1,-1,2)\)

      The center is the midpoint. The radius is half the diameter.

      \((x-3)^2+(y+2)^2+z^2=9\)

      The center is the midpoint: \[M=\dfrac{P+Q}{2}=(3,-2,0)\] The diameter is: \[ D=d(P,Q)=\sqrt{(5-1)^2+(-3--1)^2+(-2-2)^2}=\sqrt{16+4+16}=6 \] So the radius is \(r=3\) and the sphere is: \[ (x-3)^2+(y+2)^2+z^2=9 \]

    2. \(R=(3,2,6)\) and \(S=(-1,-1,-6)\)

      The center is the midpoint. The radius is half the diameter.

      \((x-1)^2+\left(y-\,\dfrac{1}{2}\right)^2+z^2=\dfrac{169}{4}\)

      The center is the midpoint: \[M=\dfrac{R+S}{2}=\left(1,\dfrac{1}{2},0\right)\] The diameter is: \[ D=d(P,Q)=\sqrt{(3--1)^2+(2--1)^2+(6--6)^2}=\sqrt{16+9+144}=13 \] So the radius is \(r=\dfrac{13}{2}\) and the sphere is: \[ (x-1)^2+\left(y-\,\dfrac{1}{2}\right)^2+z^2=\dfrac{169}{4} \]

    15. c. Polar Coordinates - 2D

  15. Convert the rectangular coordinates \((x,y)\) into polar coordinates \((r,\theta)\):

    1. \((x,y)=(3,3)\)

      The relations between rectangular coordinates \((x,y)\), the polar coordinates \((r,\theta)\) are \[\begin{array}{ll} x=r\cos\theta\qquad \qquad &r=\sqrt{x^2+y^2} \\ y=r\sin\theta&\tan\theta=\dfrac{y}{x} \end{array}\]

      \((r,\theta)=\left(3\sqrt{2}, \dfrac{\pi}{4}\right)\)

      Since the point is \((x,y)=(3,3)\) which is in the \(1^\text{st}\) quadrant, we have: \[\begin{aligned} r&=\sqrt{x^2+y^2}=\sqrt{9+9}=\sqrt{2\cdot9}=3\sqrt{2} \\ \theta&=\arctan\left(\dfrac{y}{x}\right) =\arctan\left(\dfrac{3}{3}\right) =\dfrac{\pi}{4} \end{aligned}\] So the point is: \[ (r,\theta)=\left(3\sqrt{2}, \dfrac{\pi}{4}\right) \]

    2. \((x,y)=(-2,-2\sqrt{3})\)

      Be careful to check the quadrant.

      \((r,\theta)=\left(4,\dfrac{4\pi}{3}\right)\)

      Since the point is \((x,y)=(-2,-2\sqrt{3})\), we have: \[ r=\sqrt{x^2+y^2}=\sqrt{4+12}=4 \] Notice that \((x,y)=(-2,-2\sqrt{3})\) is in quadrant III. So to find \(\theta\), we add \(\pi\) radians to the \(\arctan\): \[\begin{aligned} \theta&=\arctan\left(\dfrac{y}{x}\right)+\pi =\arctan\left(\dfrac{-2\sqrt{3}}{-2}\right)+\pi\\ &=\dfrac{\pi}{3}+\pi=\dfrac{4\pi}{3} \end{aligned}\] So the point is: \[ (r,\theta)=\left(4,\dfrac{4\pi}{3}\right) \]

    3. \((x,y)=(-2,5)\)

      The relations between rectangular coordinates \((x,y)\), the polar coordinates \((r,\theta)\) are \[\begin{array}{ll} x=r\cos\theta \qquad \qquad &r=\sqrt{x^2+y^2} \\ y=r\sin\theta&\tan\theta=\dfrac{y}{x} \end{array}\]

      \[\begin{aligned} (r,\theta)&=\left(\sqrt{29}, \arctan\left(\dfrac{5}{-2}\right)+\pi\right) \\ &\approx(5.385, 1.95\,\text{rad}) \approx(5.385,, 111.8^\circ) \end{aligned}\]

      Since the point is \((x,y)=(-2,5)\), we have: \[\begin{aligned} r&=\sqrt{x^2+y^2}=\sqrt{4+25}=\sqrt{29} \\ &\approx5.385 \end{aligned}\] Notice that \((x,y)=(-2,5)\) is in quadrant II. So to find \(\theta\), we add \(\pi\) radians to the \(\arctan\): \[\begin{aligned} \theta&=\arctan\left(\dfrac{y}{x}\right)+\pi =\arctan\left(\dfrac{5}{-2}\right)+\pi\\ &\approx 1.95\,\text{rad} \end{aligned}\] In degrees we have: \[\begin{aligned} \theta&\approx1.95\,\text{rad} \times\dfrac{180^\circ}{\pi\,\text{rad}} \\ &\approx112^\circ \end{aligned}\] So the point is: \[\begin{aligned} (r,\theta)&=\left(\sqrt{29}, \arctan\left(\dfrac{5}{-2}\right)+\pi\right) \\ &\approx(5.385, 1.95\,\text{rad}) \approx(5.385,, 112^\circ) \end{aligned}\]

    4. \((x,y)=\left(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)\)

      \((r,\theta)=\left(1,\dfrac{\pi}{3}\right)\)

      We compute: \[\begin{aligned} r&=\sqrt{x^2+y^2} =\sqrt{\left(\dfrac{1}{2}\right)^2+\left(\dfrac{\sqrt{3}}{2}\right)^2} \\ &=\sqrt{\dfrac{1}{4}+\dfrac{3}{4}}=1\\ \end{aligned}\] Since both \(x\) and \(y\) are both positive, we know that \(\left(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)\) is in quadrant \(I\) and thus we compute: \[\begin{aligned} \theta&=\arctan\left(\dfrac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}\right) \\ &=\arctan{\left(\sqrt{3}\right)} \\ &=\dfrac{\pi}{3} \end{aligned}\] So the point is: \[ (r,\theta)=\left(1,\dfrac{\pi}{3}\right) \]

      js 

  16. Convert the polar coordinates \((r,\theta)\) into rectangular coordinates \((x,y)\):

    1. \((r,\theta)=\left(4,\dfrac{\pi}{3}\right)\)

      The relations between rectangular coordinates \((x,y)\), the polar coordinates \((r,\theta)\) are \[\begin{array}{ll} x=r\cos\theta \qquad \qquad &r=\sqrt{x^2+y^2} \\ y=r\sin\theta&\tan\theta=\dfrac{y}{x} \end{array}\]

      \((x,y)=(2,2\sqrt{3})\)

      Using \(r=4\) and \(\theta=\dfrac{\pi}{3}\), we compute \[\begin{aligned} x&=r\cos(\theta)=4\cos\left(\dfrac{\pi}{3}\right) =4\cdot\dfrac{1}{2}=2 \\ y&=r\sin(\theta)=4\sin\left(\dfrac{\pi}{3}\right) =4\cdot\dfrac{\sqrt{3}}{2}=2\sqrt{3} \end{aligned}\] So the point is \((x,y)=(2,2\sqrt{3})\).

    2. \((r,\theta)=\left(3,\dfrac{\pi}{2}\right)\)

      What does \(\theta=\dfrac{\pi}{2}\) mean?

      \((x,y)=(0,3)\)

      Since \(\theta=\dfrac{\pi}{2}\), the point lies on the positive \(y\)-axis at a distance \(y=r=3\) from the origin. So the point is \((x,y)=(0,3)\). Of course the formulas would also work.

    3. \((r,\theta)=\left(2,\dfrac{5\pi}{6}\right)\)

      The transformation equations from polar \((r,\theta)\) to rectangular \((x,y)\), work in any quadrant. \[ x=r\cos\theta \qquad y=r\sin\theta \]

      \((x,y)=(-\sqrt{3},1)\)

      Using \(r=2\) and \(\theta=\dfrac{5\pi}{6}\), we compute \[\begin{aligned} x&=r\cos(\theta)=2\cos\left(\dfrac{5\pi}{6}\right) =2\cdot\dfrac{-\sqrt{3}}{2}=-\sqrt{3} \\ y&=r\sin(\theta)=2\sin\left(\dfrac{5\pi}{6}\right) =2\cdot\dfrac{1}{2}=1 \end{aligned}\] So the point is \((x,y)=(-\sqrt{3},1)\).

      Notice that \(\theta=\dfrac{5\pi}{6}\) says the point is in quadrant II which agrees with the solution. The formulas work and there is nothing special to do for quadrants II and III.

  17. Plot each polar equation as rectangular and polar plots.:

    1. \(r=2-2\sin\theta\)

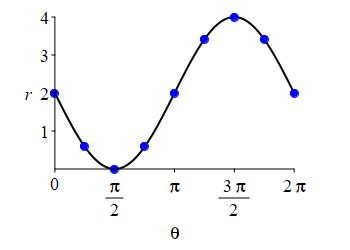
      The plot shows a sine curve fliped vertically and then shifted up by 2. There are points on the curve spread at intervals of pi over 4 along the theta-axis.   The plot shows a cardioid with its cusp at the top. It crosses the x axis at + and - 2 and crosses the y axis at 0 and -4. There are points around the cardioid at angles of pi over 4.

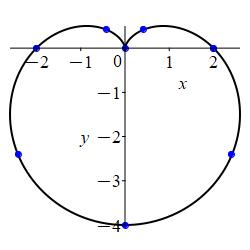
      Here is the rectangular plot of \(r=2-2\sin\theta\). Notice that \(r\) is always positive.

      The plot shows a sine curve fliped vertically and then shifted up by 2. There are points on the curve spread at intervals of pi over 4 along the theta-axis.

      To construct the polar plot, we first plot the points on the axes: \[\begin{matrix} \theta&0&\dfrac{\pi}{2}&\pi&\dfrac{3\pi}{2}&2\pi \\[10pt] r&2&0&2&4&2 \end{matrix}\] The plot also shows all multiples of \(\dfrac{\pi}{4}\).

      The plot shows points that will be on the cardioid located at angles which are multiples of pi over 4.

      We connect the points, while looking at the rectangular plot. As \(\theta\) increases from \(0\) to \(\dfrac{\pi}{2}\), \(r\) decreases from \(2\) to \(0\). Then as \(\theta\) increases from \(\dfrac{\pi}{2}\) to \(\pi\), \(r\) increases symmetrically from \(0\) back to \(2\). Next as \(\theta\) increases from \(\pi\) to\(\dfrac{3\pi}{2}\), \(r\) increases from \(2\) to \(4\). Finally, as \(\theta\) increases from \(\dfrac{3\pi}{2}\) to \(2\pi\), \(r\) decreases symmetrically from \(4\) back to \(2\).

      The plot shows a cardioid with its cusp at the top. It crosses the x axis at + and - 2 and crosses the y axis at 0 and -4. There are points around the cardioid at angles which are multiples of pi over 4.

      This curve is a cardioid oriented on the negative \(y\)-axis.

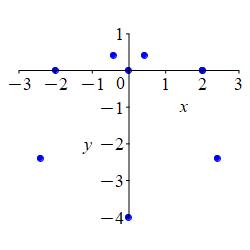
    2. \(r=2\cos\theta\)

      First plot the part where \(r \ge 0\).

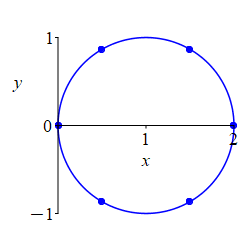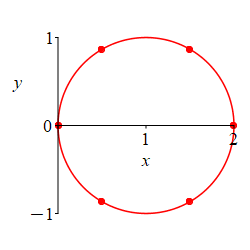
      The plot shows a cosine curve stretched vertically by a factor of 2 from -pi/2 to 3pi/2 with 12 points on the curve spread horizontally with points above the x axis colored blue and points below the x axis colored red.   The plot shows 6 points forming the vertices of a hexigon with a circle going through them. The circle has its center at 1,0 and has raduis 1. The circle and points alternate between red and blue.

      Here is the rectangular plot of \[ r=2\cos\theta \] The positive part is blue; the negative part is red.

      The plot shows a cosine curve stretched vertically by a factor of 2 from -pi/2 to 3pi/2 with 12 points on the curve spread horizontally with points above the x axis colored blue and points below the x axis colored red.

      To construct the polar plot, we first plot some interesting points for \(\dfrac{-\pi}{2} \le \theta \le \dfrac{\pi}{2}\) where \(r\) is positive: \[\begin{matrix} \theta&\dfrac{-\pi}{2}&\dfrac{-\pi}{3}&\dfrac{-\pi}{6}&0 &\dfrac{\pi}{6}&\dfrac{\pi}{3}&\dfrac{\pi}{2} \\[10pt] r&0&1&\sqrt{3}&2&\sqrt{3}&1&0 \end{matrix}\]

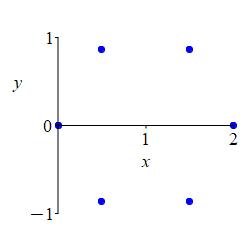
      The plot shows 6 blue points forming the vertices of a hexigon which will eventually be on a circle.

      We connect the points, while looking at the rectangular plot. As \(\theta\) increases from \(\dfrac{-\pi}{2}\) to \(0\), \(r\) increases from \(0\) to \(2\). Then as \(\theta\) increases from \(0\) to \(\dfrac{\pi}{2}\), \(r\) decreases symmetrically from \(2\) back to \(0\).

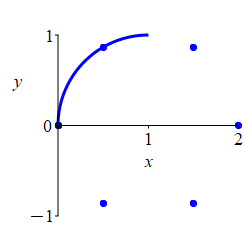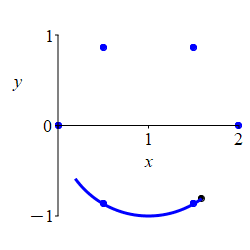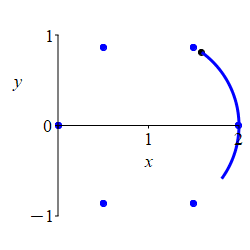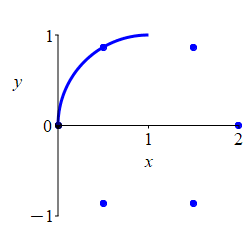
      The plot shows the same 6 blue points forming the vertices of a hexigon with a blue arc rotating counterclockwise around the circle. The circle has its center at 1,0 and has raduis 1.

      For \(\dfrac{\pi}{2} \le \theta \le \dfrac{3\pi}{2}\), \(r\) is negative and the curve retraces the previous curve.
      The plot shows the curve alternating between positive \(r\) and negative \(r\).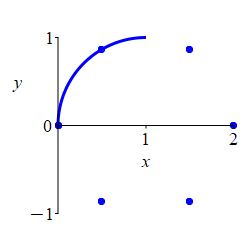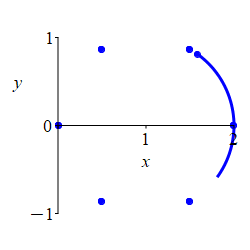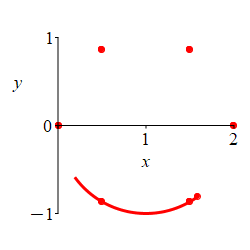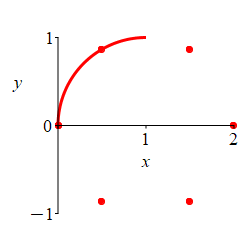

      The plot shows the same 6 blue points around the circle with the same blue arc going counterclockwise around the circle. After one full rotation the points and the arc change to red.

      Looking at the plot, we might guess that the curve is a circle. We can verify this by converting our function into rectangular coordinates: \[\begin{aligned} r=2\cos\theta \quad &\Rightarrow \quad r^2=2r\cos\theta \quad \Rightarrow \quad x^2+y^2=2x \\ &\Rightarrow \quad x^2-2x+y^2=0 \quad \Rightarrow \quad (x-1)^2+y^2=1 \end{aligned}\] This is a circle with radius \(1\) centered at \((x,y)=(1,0)\).

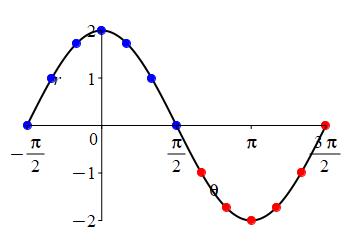
    3. \(r=\sqrt{2}-2\cos\theta\)

      Find the angles where \(r=0\).

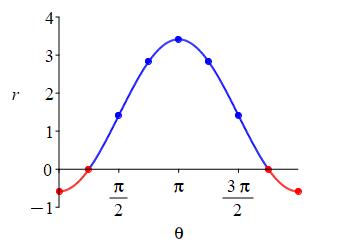
      The plot shows a cosine curve flipped vertically, then stretched vertically by a factor of 2 and finally shifted up by the square root of 2. There are points marked along the curve at multiples of pi over 2 and also where the curve crosses the x axis. The plot shows a limacon with its two loops on the left side. The outer loop is colored blue and crooses the x axis at x = -2 - sqrt of 2. The inner loop is colored red and crosses the x axis at x = - 2 + sqrt of 2.

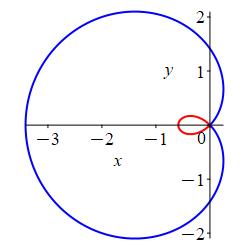
      Here is the rectangular plot of \(r=\sqrt{2}-2\cos\theta\).

      The plot shows a cosine curve flipped vertically, then stretched vertically by a factor of 2 and finally shifted up by the square root of 2. There are points marked along the curve at multiples of pi over 2 and also where the curve crosses the x axis.

      Before constructing the polar plot, we find the points where the radius is \(0\): \[ r=\sqrt{2}-2\cos\theta=0 \quad \Rightarrow \quad \cos\theta=\dfrac{\sqrt{2}}{2} \quad \Rightarrow \quad \theta=\dfrac{\pi}{4}, \dfrac{7\pi}{4} \]

      For the polar plot, we first plot the points on the axes and mark the angles where \(r=0\): \[\begin{matrix} \theta&0&\dfrac{\pi}{4}&\dfrac{\pi}{2}&\pi &\dfrac{3\pi}{2}&\dfrac{7\pi}{4}&2\pi \\[10pt] r&\sqrt{2}-2&0&\sqrt{2}&\sqrt{2}+2&\sqrt{2}&0&\sqrt{2}-2 \end{matrix}\]

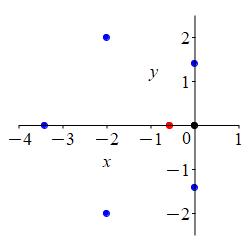
      The plot shows five blue points distributed as a pentagon with 2 on the y-axis and 3 to the left of the y axis plus one red point on the negative x-axis inside the pentagon.

      We connect the points, while looking at the rectangular plot. First the pieces where \(r \ge 0\): As \(\theta\) increases from \(\dfrac{\pi}{6}\) to \(\dfrac{\pi}{2}\), \(r\) increases from \(0\) to \(\sqrt{2}\). Next as \(\theta\) increases from \(\dfrac{\pi}{2}\) to \(\pi\), \(r\) increases from \(\sqrt{2}\) to \(\sqrt{2}+2\). Then as \(\theta\) increases from \(\pi\) to \(\dfrac{11\pi}{6}\), \(r\) decreases symmetrically from \(\sqrt{2}+2\) back to \(0\).

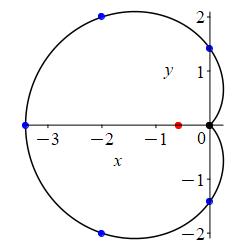
      The plot shows the 6 points from the previous plot. The five blue points are connected by the outer loop of a limacon.

      Now for the pieces where \(r \le 0\): At \(\theta=0\) which is the positive \(x\)-axis, \(r=\sqrt{2}-2\) which is negative. So we move \(2-\sqrt{2}\) along the negative \(x\)-axis. As \(\theta\) increases from \(0\) to \(\dfrac{\pi}{6}\), \(r\) changes from \(\sqrt{2}-2\) to \(0\) forming the lower half of the small loop. Similarly, as \(\theta\) increases from \(\dfrac{11\pi}{6}\) to \(2\pi\), \(r\) changes symmetrically from \(0\) to \(\sqrt{2}-2\) forming the upper half of the small loop.

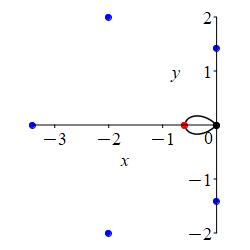
      The plot shows the 6 points from the previous plot. This time the single red point is at the tip of the inner loop of the limacon.

      All together, we have:

      The plot shows the limacon, with the outer loop colored blue and the inner loop colored red.

      We identify the curve as a limacon with large radius \(r=\sqrt{2}+2\) and small radius \(r=2-\sqrt{2}\) since \(\sqrt{2}-2\) is negative!

    4. \(r=2-\cos\theta\)

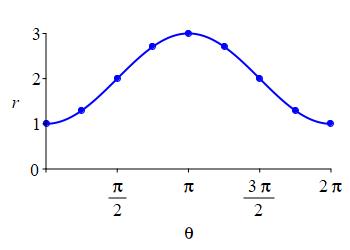
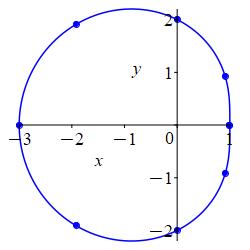
      The plot shows a cosine curve flipped vertically and shifted upward by 2.   The plot shows 8 points distributed around a limacon without an inner loop. It looks a little like a circle but flattened on the right.

      Here is the rectangular plot of \(r=2-\cos\theta\). Notice that \(r\) oscillates between \(1\) and \(3\).

      The plot shows a cosine curve flipped vertically and shifted upward by 2.

      We plot the points on the axes where the values are: \[\begin{matrix} \theta&0&\dfrac{\pi}{2}&\pi&\dfrac{3\pi}{2}&2\pi \\[10pt] r&1&2&3&2&1 \end{matrix}\] as well as some extra points at multiples of \(\pi/4\).

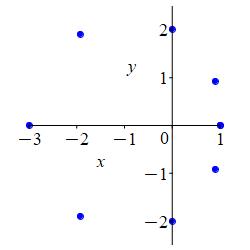
      The plot shows 8 points distributed radially with the three points to the right of the y-axis being closer to the y-axis than the three to left of it.

      We connect the points, while looking at the rectangular plot. As \(\theta\) increases from \(0\) through \(\dfrac{\pi}{2}\) to \(\pi\), \(r\) increases from \(1\) through \(2\) to \(3\). Then as \(\theta\) increases from \(\pi\) through \(\dfrac{3\pi}{2}\) to \(2\pi\), \(r\) decreases symmetrically from \(3\) through \(2\) back to \(0\).

      The plot shows 8 points distributed around a limacon without an inner loop. It looks a little like a circle but flattened on the right.

      Even though there is no inner loop, this curve is still called a limacon. Its large radius is \(r=3\) and its small radius is \(r=1\).

    5. \(r=\sin^2\theta-\cos^2\theta\)

      Re-express the equation using a trig identity.

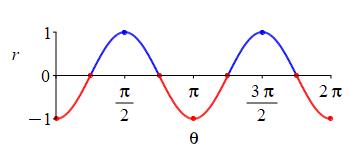
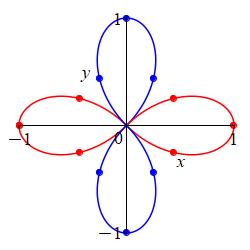
      The plot shows a cosine curve flipped vertically and shrunk horizontally by a factor of 2 with the parts below the x-axis colored red and the parts above the x-axis colored blue. The plot shows a four leafed rose with the petals along the 4 axes. The left and right leaves are colored red and the top and bottom leaves are colored blue.

      We use the trig identity \(\cos2\theta=\cos^2\theta-\sin^2\theta\), to rewrite the equation as \(r=-\cos2\theta\). We recall \(r=\cos2\theta\) is the \(4\)-leaf rose. The extra minus sign only reverses when the left and right petals are drawn and when the top and bottom petals are drawn.

      The plot shows a cosine curve flipped vertically and shrunk horizontally by a factor of 2 with the parts below the x-axis colored red and the parts above the x-axis colored blue. The plot shows a four leafed rose with the petals along the 4 axes. The left and right leaves are colored red and the top and bottom leaves are colored blue.

  18. Plot each polar equation as rectangular and polar plots.

    These plots are similar to the roses but behave differently.

    1. \(r=1+2\cos2\theta\)

      The polar form of \(r=2\cos2\theta\) will be a rose with uniform pedals.
      Plot the vertically shifted \(r=1+2\cos2\theta\) in rectangular coordinates and determine how it will affect the shape of the rose.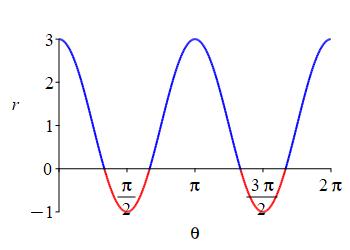

      The plot shows a cosine curve stretched vertically by a factor of 2 and then shifted up by 1 and also shrunk horizontally by a factor of 2. The parts of the curve below the x-axis colored red and the parts above the x-axis colored blue. The plot shows a four leaf rose. The top and bottom leaves are colored red and are smaller. The left and right leaves are colored blue and are larger.
      The rectangular form of \(r=1+2\cos2\theta\) is a cosine curve with amplitude stretched to \(2\) and then shifted up by \(1\) and also shrunk horizontally by a factor of 2. The \(x\)-axis divides the curve into positive and negative parts.

      Notably, the negative portion is 'smaller' than the postive portion.

      The plot shows a cosine curve stretched vertically by a factor of 2 and then shifted up by 1 and also shrunk horizontally by a factor of 2. The parts of the curve below the x-axis colored red and the parts above the x-axis colored blue.

      For the usual \(4\)-leaf rose, the positive and negative petals have the same size. Here the vertical shift of the rectangular form causes the positive petals to grow and the negative petals to shrink.

      Larger pedals are positive.
      Smaller pedals are negative.

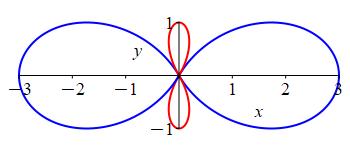
      The plot shows a four leaf rose. The top and bottom leaves are colored red and are smaller. The left and right leaves are colored blue and are larger.

    2. \(r=1+2\cos3\theta\)

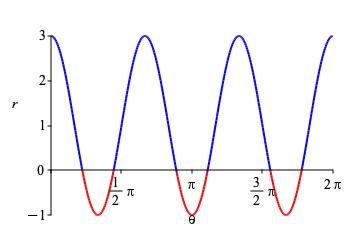
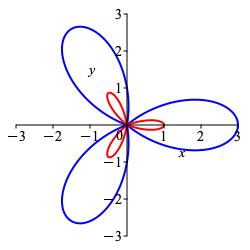      The plot shows a cosine curve stretched vertically by a factor of 2 and then shifted up by 1 and also shrunk horizontally by a factor of 3. The parts of the curve below the x-axis colored red and the parts above the x-axis colored blue. The plot shows a six leaf rose with three small red loops contained within three big blue loops.
      The rectangular form of \(r=1+2\cos3\theta\) is a sine curve with amplitude stretched to \(2\) and then shifted up by \(1\). The increased frequency compresses the curve in the \(x\)-direction. So there are more oscillations in the interval \([0, 2\pi]\). The \(x\)-axis divides the curve into positive and negative parts, but the negative bumps are “smaller” than the postive bumps. The bumps in the rectangular plot become petals on the polar plot, and the negative petals are smaller than the positive petals.
      The plot shows a cosine curve stretched vertically by a factor of 2 and then shifted up by 1 and also shrunk horizontally by a factor of 3. The parts of the curve below the x-axis colored red and the parts above the x-axis colored blue.

      The unshifted variation of this function, \(r=2\cos3\theta\) is a uniform \(3\)-leaf rose with the negative petals retracing the positive ones. Here the negative bumps are smaller, so the “retraced” petals are smaller.

      Larger pedals are positive.
      Smaller pedals are negative.

      The plot shows a six leaf rose with three small red loops contained within three big blue loops.

    3. Predict the number, sizes and positions of the leaves in a plot of \(r=1+2\cos(n\theta)\), if \(n\) is even. Explain.

      Compare the function \(r=1+2\cos(n\theta)\) at any point \(\theta\) and at \(\theta + \pi\). Is the radius for both values positive? Both negative? Opposite signs?

      When \(n\) is even, there will be \(2n\) leaves with \(n\) large leaves and \(n\) small leaves between them.

      We begin by understanding the behaviour of a uniform rose, \(r=2\cos(n\theta)\). On the interval \([0,2\pi]\), there are \(n\) positive bumps and \(n\) negative bumps, which produce \(2n\) petals. When \(n\) is even, the negative bumps trace unique petals, and do not retrace the positive petals. See the solution of Exercise 11 on the polar plot page.

      For the shifted version \(r=1+2\cos(n\theta)\), the positive petals grow and the negative petals shrink. For further evidence, the polar plot of \(r=1+2\cos 4θ\) has \(8\) petals:

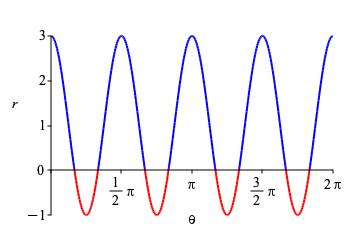
      The plot shows a cosine curve stretched vertically by a factor of 2 and shrunk horizontally by a factor of 4. The parts of the curve that are below the x-axis are colored red and the parts that are above the x-axis are colored blue.
      \(8\)-Leaf Rose:   \(r=\cos(4\theta)\)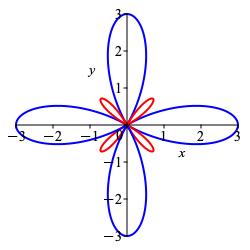
      The plot shows an eight leaf rose with the loops along the axes colored blue and the loops in the diagonal directions colored red and much smaller.

    4. Predict the number, sizes and positions of the leaves in a plot of \(r=1+2\cos(n\theta)\), if \(n\) is odd. Explain.

      Compare the function \(r=1+2\cos(n\theta)\) at any point \(\theta\) and at \(\theta + \pi\). Is the radius for both values positive? Both negative? Opposite signs?

      When \(n\) is odd, there will be \(2n\) leaves with \(n\) large leaves and \(n\) small leaves inside them.

      We begin by understanding the behaviour of a uniform rose, \(r=2\cos(n\theta)\). On the interval \([0,2\pi]\), there are \(n\) positive bumps and \(n\) negative bumps, which produce \(2n\) petals. When \(n\) is odd, the negative petals retrace the positive petals. See the solution of Exercise 12 on the polar plot page.

      For the shifted version \(r=1+2\cos(n\theta)\), the positive petals grow and the negative petals shrink but are inside the positive ones. For further evidence, the polar plot of \(r=1+2\cos 5θ\) has \(10\) petals:

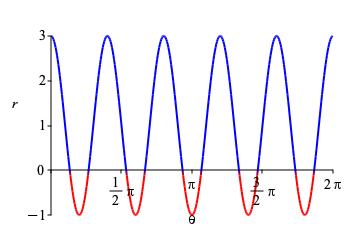
      The plot shows a cosine curve stretched vertically by a factor of 2 and shrunk horizontally by a factor of 5 and shifted up by 1. The parts of the curve that are below the x-axis are colored red and the parts that are above the x-axis are colored blue.
      \(10\)-Leaf Rose:   \(r=\cos(5\theta)\)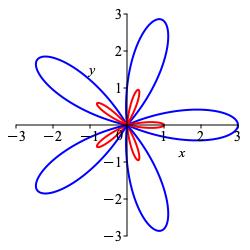
      The plot shows a ten leaf rose with five small blue loops contained in 5 larger red loops.
  19. Convert each polar equation into a rectangular equation and, if possible, identify the curve:

    1. \(r=4\cos(\theta)\)

      Recall: \(\quad \cos\theta=\dfrac{x}{r} \quad \text{and} \quad r=\sqrt{x^2+y^2}\)

      In rectangular coordinates, the equation is \((x-2)^2+y^2=4\). The curve is a circle of radius \(2\) centered at \((2,0)\).

      The plot shows a circle with radius 2 centered at 2,0.

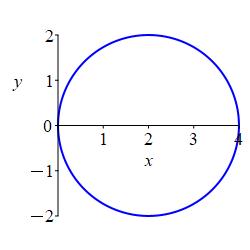
      Multiply both sides of \(r=4\cos\theta\) by \(r\) and substitute \(r^2=x^2+y^2\) and \(r\cos\theta=x\). Then complete the square on \(x\): \[\begin{aligned} r^2=4r\cos\theta \\ x^2+y^2=4x \\ (x-2)^2+y^2=4 \end{aligned}\] This is a circle of radius \(2\) centered at \((2,0)\).

      The plot shows a circle with radius 2 centered at 2,0.

    2. \(r=\sec\theta\tan\theta\)

      Recall:   \(\tan\theta=\dfrac{y}{x}\) and \(\sec\theta=\dfrac{r}{x}\)
      Remember, when you cancel an \(r\), you must retain the origin as a solution.

      The curve is the parabola \(y=x^2\) which passes through the origin and opens to the upward.

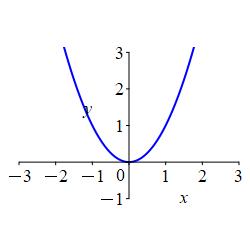
      The plot shows a parabola centered on the y-axis.

      In \(r=\sec\theta\tan\theta\), we substitute \(\sec\theta=\dfrac{r}{x}\) and \(\tan\theta=\dfrac{y}{x}\). Then we multiply both sides by \(x^2\): \[\begin{aligned} r=\dfrac{r}{x}\dfrac{y}{x} \\ x^2 r=r y \end{aligned}\] We cancel an \(r\), but must remember to check the origin is also a solution. We obtain \(x^2=y\) and note that the origin, \((0,0)\), is still a solution. So the curve is the parabola \(y=x^2\) which passes through the origin and opens to the upward.

      The plot shows a parabola centered on the y-axis.

    3. \(r^2\cos(2\theta)=1\)

      Use a trig identity for \(\cos(2\theta)\).

      The curve is the hyperbola \(x^2-y^2=1\) which opens left and right.

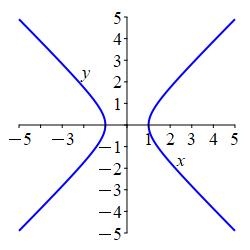
      The plot shows a hyperbola opening left and right centered on the y-axis.

      In \(r^2\cos(2\theta)=1\), we use the trig identity \(\cos(2\theta)=\cos^2\theta-\sin^2\theta\) and distribute the \(r^2\): \[ r^2\cos^2\theta-r^2\sin^2\theta=1 \] This is \[ x^2-y^2=1 \] which is a hyperbola opening left and right.

      The plot shows a hyperbola opening left and right centered on the y-axis.

      Note that either of the identities \(\cos(2\theta)=2\cos^2\theta-1\) or \(\cos(2\theta)=1-2\sin^2\theta\) would also work.

  20. Convert each rectangular equation into a polar equation and, if possible, identify the curve:

    1. \((x^2+y^2)^3=4x^2y^2\)

      Recall:   \(x=r\cos\theta\), \(y=r\sin\theta\) and \(x^2+y^2=r^2\).

      The curve is \(r=\sin(2\theta)\) which is a 4 leaf rose with one leaf in each quadrant.

      The plot shows a four leafed rose with one leaf in each quadrant.

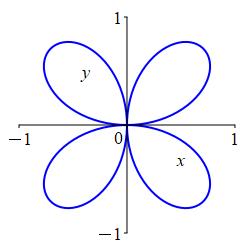
      We substitute \(x=r\cos\theta\), \(y=r\sin\theta\) and \(x^2+y^2=r^2\) into \((x^2+y^2)^3=4x^2y^2\) to get \[ r^6=4r^2\cos^2\theta\,r^2\sin^2\theta \] We take the square root of both sides: \[ r^3=2r^2\cos\theta\sin\theta \] If we divide both sides by \(r^2\), we get \(r=2\cos\theta\sin\theta\) but we need to check that the origin is still a solution. It is because \((r,\theta)=(0,0)\) is a solution. Finally, we use the identity, \(\sin(2\theta)=2\cos\theta\sin\theta\), to rewrite the equation as: \[ r=\sin(2\theta) \] which we recognize this as a \(4\) leaf rose with one leaf in each quadrant.

      The plot shows a four leafed rose with one leaf in each quadrant.

    2. \((x^2+y^2)^3=(x^2-y^2)^2\)

      Recall:   \(x=r\cos\theta\), \(y=r\sin\theta\) and \(x^2+y^2=r^2\).

      The curve is \(r=\cos(2\theta)\) which is a 4 leaf rose with one leaf on each half-axis.

      The plot shows a four leafed rose with one leaf on each half-axis.

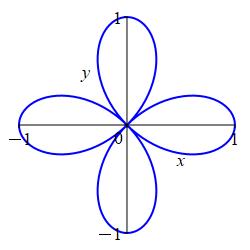
      We substitute \(x=r\cos\theta\), \(y=r\sin\theta\) and \(x^2+y^2=r^2\) into \((x^2+y^2)^3=(x^2-y^2)^2\) to get \[ r^6=(r^2\cos^2\theta-r^2\sin^2\theta)^2 \] We take the square root of both sides and use the identity \(\cos^2\theta-\sin^2\theta=\cos(2\theta)\): \[\begin{aligned} r^3&=r^2\cos^2\theta-r^2\sin^2\theta \\ &=r^2\cos(2\theta) \end{aligned}\] Next, we divide by \(r^2\) and check the orign is still a solution because \((r,\theta)=\left(0,\dfrac{\pi}{4}\right)\) is a solution. \[ r=\cos(2\theta) \] We recognize this as a \(4\) leaf rose with one leaf on each half-axis.

      The plot shows a four leafed rose with one leaf on each half-axis.

    21. d. Cylindrical and Spherical Coordinates - 3D and nD

  21. Convert the rectangular coordinates \((x,y,z)\) into cylindrical coordinates \((r,\theta,z)\) and spherical coordinates \((\rho,\phi,\theta)\):

    1. \((x,y,z)=(-\sqrt{2},\sqrt{2},2\sqrt{3})\)

      The conversion from rectangular \((x,y,z)\) to cylindrical \((r,\theta,z)\) coordinates is: \[ r=\sqrt{x^2+y^2} \qquad \tan\theta=\dfrac{y}{x} \qquad z=z \] The conversion from rectangular \((x,y,z)\) to spherical \((\rho,\phi,\theta)\) coordinates is: \[\begin{aligned} \rho&=\sqrt{x^2+y^2+z^2} \\ \phi&=\arccos\left(\dfrac{z}{\sqrt{x^2+y^2+z^2}}\right) =\arccos\left(\dfrac{z}{\rho}\right) \\ \tan\theta&=\dfrac{y}{x} \end{aligned}\]

      \((r,\theta,z)=\left(2,\dfrac{3\pi}{4},2\sqrt{3}\right)\)
      \((\rho,\phi,\theta)=\left(4,\dfrac{\pi}{6},\dfrac{3\pi}{4}\right)\)

      The point is \((x,y,z)=(-\sqrt{2},\sqrt{2},2\sqrt{3})\).

      To convert to cylindrical coordinates, we compute: \[\begin{aligned} r&=\sqrt{x^2+y^2}=\sqrt{2+2}=2 \\ \tan\theta&=\dfrac{y}{x}=\dfrac{\sqrt{2}}{-\sqrt{2}}=-1 \end{aligned}\] Since the point \((x,y)=(-\sqrt{2},\sqrt{2})\) is in the second quadrant: \[ \theta=\arctan(-1)+\pi=\dfrac{-\pi}{4}+\pi=\dfrac{3\pi}{4} \] So the cylindrical coordinates are: \[ (r,\theta,z)=\left(2,\dfrac{3\pi}{4},2\sqrt{3}\right) \]

      To convert to spherical coordinates, we compute: \[\begin{aligned} \rho&=\sqrt{x^2+y^2+z^2}=\sqrt{2+2+12}=4 \\ \phi&=\arccos\left(\dfrac{z}{\rho}\right) =\arccos\left(\dfrac{2\sqrt{3}}{4}\right)=\dfrac{\pi}{6} \end{aligned}\] So the spherical coordinates are: \[ (\rho,\phi,\theta)=\left(4,\dfrac{\pi}{6},\dfrac{3\pi}{4}\right) \]

    2. \((x,y,z)=(\sqrt{3},-1,2)\)

      \((r,\theta,z)=\left(2,-\,\dfrac{\pi}{6},2\right)\)
      \((\rho,\phi,\theta)=\left(2\sqrt{2},\dfrac{\pi}{4},-\,\dfrac{\pi}{6}\right)\)

      The point is \((x,y,z)=(\sqrt{3},-1,2)\).

      To convert to cylindrical coordinates, we compute: \[\begin{aligned} r&=\sqrt{x^2+y^2}=\sqrt{3+1}=2 \\ \tan\theta&=\dfrac{y}{x}=\dfrac{-1}{\sqrt{3}} \end{aligned}\] Since the point \((x,y)=(\sqrt{3},-1)\) is in the fourth quadrant: \[ \theta=\arctan\left(\dfrac{-1}{\sqrt{3}}\right)=-\,\dfrac{\pi}{6} \] So the cylindrical coordinates are: \[ (r,\theta,z)=\left(2,-\,\dfrac{\pi}{6},2\right) \]

      To convert to spherical coordinates, we compute: \[\begin{aligned} \rho&=\sqrt{x^2+y^2+z^2}=\sqrt{3+1+4}=2\sqrt{2} \\ \phi&=\arccos\left(\dfrac{z}{\rho}\right) =\arccos\left(\dfrac{2}{2\sqrt{2}}\right)=\dfrac{\pi}{4} \end{aligned}\] So the spherical coordinates are: \[ (\rho,\phi,\theta)=\left(2\sqrt{2},\dfrac{\pi}{4},-\,\dfrac{\pi}{6}\right) \]

    3. \((x,y,z)=(4,3,-12)\)

      \((r,\theta,z)=\left(5,\arctan\left(\dfrac{3}{4}\right),-12\right)\)
      \((\rho,\phi,\theta)=\left(13,\arccos\left(\dfrac{-12}{13}\right), \arctan\left(\dfrac{3}{4}\right)\right)\)

      The point is \((x,y,z)=(4,3,-12)\).

      To convert to cylindrical coordinates, we compute: \[\begin{aligned} r&=\sqrt{x^2+y^2}=\sqrt{16+9}=5 \\ \tan\theta&=\dfrac{y}{x}=\dfrac{3}{4} \end{aligned}\] Since the point \((x,y)=(4,3)\) is in the first quadrant: \[ \theta=\arctan\left(\dfrac{3}{4}\right) \] So the cylindrical coordinates are: \[ (r,\theta,z)=\left(5,\arctan\left(\dfrac{3}{4}\right),-12\right) \]

      To convert to spherical coordinates, we compute: \[\begin{aligned} \rho&=\sqrt{x^2+y^2+z^2}=\sqrt{16+9+144}=13 \\ \phi&=\arccos\left(\dfrac{z}{\rho}\right) =\arccos\left(\dfrac{-12}{13}\right) \end{aligned}\] So the spherical coordinates are: \[ (\rho,\phi,\theta)=\left(13,\arccos\left(\dfrac{-12}{13}\right), \arctan\left(\dfrac{3}{4}\right)\right) \]

  22. Convert the cylindrical coordinates \((r,\theta,z)\) into rectangular coordinates \((x,y,z)\) and spherical coordinates \((\rho,\phi,\theta)\):

    1. \((r,\theta,z)=\left(3,\dfrac{3\pi}{4},-4\right)\)

      The conversion from cylindrical \((r,\theta,z)\) to rectangular \((x,y,z)\) coordinates is: \[ x=r\cos\theta \qquad y=r\sin\theta \qquad z=z \] The conversion from cylindrical \((r,\theta,z)\) to spherical \((\rho,\phi,\theta)\) coordinates is: \[\begin{aligned} \rho&=\sqrt{r^2+z^2} \\ \phi&=\arccos\left(\dfrac{z}{\sqrt{r^2+z^2}}\right) =\arccos\left(\dfrac{z}{\rho}\right) \\ \theta&=\theta \end{aligned}\]

      \((x,y,z)=\left(-\,\dfrac{3}{\sqrt{2}},\dfrac{3}{\sqrt{2}},-4\right)\)
      \((\rho,\phi,\theta)=\left(5,\arccos\left(\dfrac{-4}{5}\right), \dfrac{3\pi}{4}\right)\)

      The point is \((r,\theta,z)=\left(3,\dfrac{3\pi}{4},-4\right)\).

      To convert to rectangular coordinates, we compute: \[\begin{aligned} x&=r\cos\theta=3\cos\left(\dfrac{3\pi}{4}\right)=-\,\dfrac{3}{\sqrt{2}} \\ y&=r\sin\theta=3\sin\left(\dfrac{3\pi}{4}\right)=\dfrac{3}{\sqrt{2}} \end{aligned}\] So the rectangular coordinates are: \[ (x,y,z)=\left(-\,\dfrac{3}{\sqrt{2}},\dfrac{3}{\sqrt{2}},-4\right) \]

      Since the angle \(\theta=\dfrac{3\pi}{4}\) is in the second quadrant, we know \(x<0\) and \(y>0\), which agrees with our answers.

      To convert to spherical coordinates, we compute: \[\begin{aligned} \rho&=\sqrt{r^2+z^2}=\sqrt{9+16}=5 \\ \phi&=\arccos\left(\dfrac{z}{\rho}\right) =\arccos\left(\dfrac{-4}{5}\right) \end{aligned}\] So the spherical coordinates are: \[ (\rho,\phi,\theta)=\left(5,\arccos\left(\dfrac{-4}{5}\right),\dfrac{3\pi}{4}\right) \]

    2. \((r,\theta,z)=\left(6,\dfrac{2\pi}{3},-6\right)\)

      \((x,y,z)=(-3,3\sqrt{3},-6)\)
      \((\rho,\phi,\theta)=\left(6\sqrt{2},\dfrac{3\pi}{4},\dfrac{2\pi}{3}\right)\)

      The point is \((r,\theta,z)=\left(6,\dfrac{2\pi}{3},-6\right)\).

      To convert to rectangular coordinates, we compute: \[\begin{aligned} x&=r\cos\theta=6\cos\left(\dfrac{2\pi}{3}\right)=6\cdot\dfrac{-1}{2}=-3 \\ y&=r\sin\theta=6\sin\left(\dfrac{2\pi}{3}\right)=6\cdot\dfrac{\sqrt{3}}{2}=3\sqrt{3} \end{aligned}\] So the rectangular coordinates are: \[ (x,y,z)=(-3,3\sqrt{3},-6) \]

      Since the angle \(\dfrac{2\pi}{3}\) is in the second quadrant, we know \(x<0\) and \(y>0\), which agrees with our answers.

      To convert to spherical coordinates, we compute: \[\begin{aligned} \rho&=\sqrt{r^2+z^2}=\sqrt{36+36}=6\sqrt{2} \\ \phi&=\arccos\left(\dfrac{z}{\rho}\right) =\arccos\left(\dfrac{-6}{6\sqrt{2}}\right)=\dfrac{3\pi}{4} \end{aligned}\] So the spherical coordinates are: \[ (\rho,\phi,\theta)=\left(6\sqrt{2},\dfrac{3\pi}{4},\dfrac{2\pi}{3}\right) \]

    3. \((r,\theta,z)=\left(2\sqrt{2},\dfrac{-\pi}{4},1\right)\)

      \((x,y,z)=(2,-2,1)\)
      \((\rho,\phi,\theta)=\left(3,\arccos\left(\dfrac{1}{3}\right),\dfrac{-\pi}{4}\right)\)

      The point is \((r,\theta,z)=\left(2\sqrt{2},\dfrac{-\pi}{4},1\right)\).

      To convert to rectangular coordinates, we compute: \[\begin{aligned} x&=r\cos\theta=2\sqrt{2}\cos\left(\dfrac{-\pi}{4}\right)=2 \\ y&=r\sin\theta=2\sqrt{2}\sin\left(\dfrac{-\pi}{4}\right)=-2 \end{aligned}\] So the rectangular coordinates are: \[ (x,y,z)=(2,-2,1) \]

      Since the angle \(\dfrac{-\pi}{4}\) is in the fourth quadrant, we know \(x>0\) and \(y<0\), which agrees with our answers.

      To convert to spherical coordinates, we compute: \[\begin{aligned} \rho&=\sqrt{r^2+z^2}=\sqrt{8+1}=3 \\ \phi&=\arccos\left(\dfrac{z}{\rho}\right) =\arccos\left(\dfrac{1}{3}\right) \end{aligned}\] So the spherical coordinates are: \[ (\rho,\phi,\theta)=\left(3,\arccos\left(\dfrac{1}{3}\right),\dfrac{-\pi}{4}\right) \]

  23. Convert the spherical coordinates \((\rho,\phi,\theta)\) into rectangular coordinates \((x,y,z)\) and cylindrical coordinates \((r,\theta,z)\):

    1. \((\rho,\phi,\theta)=\left(4,\dfrac{2\pi}{3},\dfrac{\pi}{4}\right)\)

      The conversion from spherical \((\rho,\phi,\theta)\) to rectangular \((x,y,z)\) coordinates is: \[ x=\rho\sin\phi\cos\theta \quad y=\rho\sin\phi\sin\theta \quad z=\rho\cos\phi \] The conversion from spherical \((\rho,\phi,\theta)\) to cylindrical \((r,\theta,z)\) coordinates is: \[ r=\rho\sin\phi \quad \theta=\theta \quad z=\rho\cos\phi \]

      \((x,y,z)=(\sqrt{6},\sqrt{6},-2)\)
      \((r,\theta,z)=\left(2\sqrt{3},\dfrac{\pi}{4},-2\right)\)

      The point is \((\rho,\phi,\theta)=\left(4,\dfrac{2\pi}{3},\dfrac{\pi}{4}\right)\).

      To convert to rectangular coordinates, we compute: \[\begin{aligned} x&=\rho\sin\phi\cos\theta =4\sin\left(\dfrac{2\pi}{3}\right)\cos\left(\dfrac{\pi}{4}\right) =4\dfrac{\sqrt{3}}{2}\dfrac{1}{\sqrt{2}} =\sqrt{6} \\ y&=\rho\sin\phi\sin\theta =4\sin\left(\dfrac{2\pi}{3}\right)\sin\left(\dfrac{\pi}{4}\right) =4\dfrac{\sqrt{3}}{2}\dfrac{1}{\sqrt{2}} =\sqrt{6} \\ z&=\rho\cos\phi=4\cos\left(\dfrac{2\pi}{3}\right)=4\dfrac{-1}{2}=-2 \end{aligned}\] So the rectangular coordinates are: \[ (x,y,z)=(\sqrt{6},\sqrt{6},-2) \]

      Since the polar angle is \(\phi=\dfrac{2\pi}{3}>\dfrac{\pi}{2}\), the point is in the lower hemisphere, i.e. \(z<0\) which it is.
      Since the azimuthal angle is \(\theta=\dfrac{\pi}{4}\), the \(x\) and \(y\) coordinates should be equal, which they are.

      To convert to cylindrical coordinates, we compute: \[ r=\rho\sin\phi=4\sin\left(\dfrac{2\pi}{3}\right)=2\sqrt{3} \] So the cylindrical coordinates are: \[ (r,\theta,z)=\left(2\sqrt{3},\dfrac{\pi}{4},-2\right) \]

    2. \((\rho,\phi,\theta)=\left(10,\dfrac{\pi}{2},\dfrac{\pi}{6}\right)\)

      \((x,y,z)=(5\sqrt{3},5,0)\)
      \((r,\theta,z)=\left(10,\dfrac{\pi}{6},0\right)\)

      The point is \((\rho,\phi,\theta)=\left(10,\dfrac{\pi}{2},\dfrac{\pi}{6}\right)\).

      To convert to rectangular coordinates, we compute: \[\begin{aligned} x&=\rho\sin\phi\cos\theta =10\sin\left(\dfrac{\pi}{2}\right)\cos\left(\dfrac{\pi}{6}\right) =10\dfrac{\sqrt{3}}{2} =5\sqrt{3} \\ y&=\rho\sin\phi\sin\theta =10\sin\left(\dfrac{\pi}{2}\right)\sin\left(\dfrac{\pi}{6}\right) =10\dfrac{1}{2} =5 \\ z&=\rho\cos\phi=10\cos\left(\dfrac{\pi}{2}\right)=0 \end{aligned}\] So the rectangular coordinates are: \[ (x,y,z)=(5\sqrt{3},5,0) \]

      Since the polar angle is \(\phi=\dfrac{\pi}{2}\), the point is in the \(xy\)-plane, i.e. \(z=0\).

      To convert to cylindrical coordinates, we compute: \[ r=\rho\sin\phi=10\sin\left(\dfrac{\pi}{2}\right)=10 \] So the cylindrical coordinates are: \[ (r,\theta,z)=\left(10,\dfrac{\pi}{6},0\right) \]

  24. Plot each surface given in cylindrical coordinates, \((r,\theta,z)\). Notice there is no \(\theta\) in the equation. So the shape is obtained by rotating a curve about the \(z\)-axis. Identify the shape of the surface.

    1. \(z=\dfrac{r}{\sqrt{3}}\)

      What is this shape in the \(rz\)-plane?

      Cone centered on the \(z\)-axis opening at \(60^\circ\).

      The plot shows a cone centered on the z-axis.

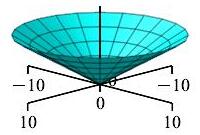
      In an \(rz\)-plane for any fixed \(\theta\), the equation \(z=\dfrac{r}{\sqrt{3}}\) is a straight line and the angle away from the \(z\)-axis is: \[ \phi=\arctan\dfrac{r}{z}=\arctan\sqrt{3}=\dfrac{\pi}{3} \]

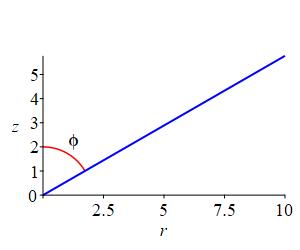
      The plot shows a line going up and to the right with its angle from the y-axis shown as phi.

      Since this is true for all \(\theta\), we rotate about the \(z\)-axis sweeping out a cone centered on the \(z\)-axis opening at \(\dfrac{\pi}{3}=60^\circ\).

      The plot shows a cone centered on the z-axis with angle phi = pi over 3.

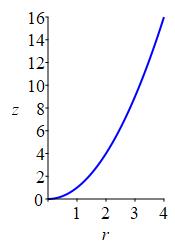
    2. \(z=r^2\)

      What is this shape in the \(rz\)-plane?

      Bowl shape (paraboloid) opening up along the positive \(z\)-axis.

      The plot shows a paraboloid centered on the z-axis opening along the positive z-axis.

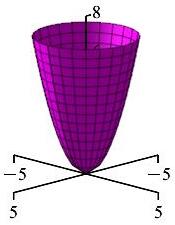
      In an \(rz\)-plane for any fixed \(\theta\), the equation \(z=r^2\) is a parabola opening along the positive \(z\)-axis.

      The plot shows a parabola opening along the z-axis which goes up.

      Since this is true for all \(\theta\), we rotate about the \(z\)-axis sweeping out a bowl (also known as a paraboloid) centered on the \(z\)-axis opening along the positive \(z\)-axis.

      The plot shows a paraboloid centered on the z-axis opening along the positive z-axis.

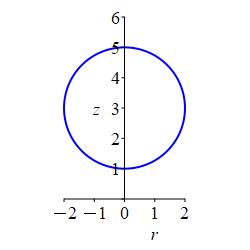
    3. \(r^2+(z-3)^2=4\)

      What is this shape in the \(rz\)-plane?

      Sphere of radius \(2\) centered at \(z=3\).

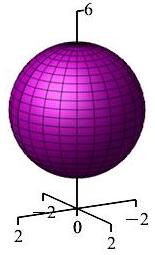
      The plot shows a sphere with radius 2 centered at 0,0,3.

      In an \(rz\)-plane for any fixed \(\theta\), the equation \(r^2+(z-3)^2=4\) is a circle of radius \(2\) centered at \((r,z)=(0,3)\).

      The plot shows a circle with radius 2 centered at 0,3

      Since this is true for all \(\theta\), we rotate about the \(z\)-axis sweeping out a sphere of radius \(2\) centered at \((x,y,z)=(0,0,3)\).

      The plot shows a sphere with radius 2 centered at 0,0,3.

    4. \((r-3)^2+z^2=4\)

      What is this shape in the \(rz\)-plane?

      Donut (torus) of radius \(2\) whose central
      circle is in the \(xy\)-plane has radius \(3\)
      and is centered at the origin.

      The plot shows a donut (or torus) of radius 2 whose central circle is in the xy-plane with radius 3 and center at the origin.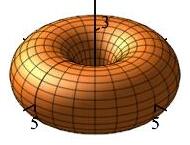

      In an \(rz\)-plane for any fixed \(\theta\), the equation \((r-3)^2+z^2=4\) is a circle of radius \(2\) centered at \((r,z)=(3,0)\).

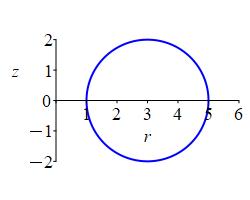
      The plot shows a circle with radius 2 centered at 3,0.

      Since this is true for all \(\theta\), we rotate about the \(z\)-axis sweeping out a donut (or torus) of radius \(2\) whose central circle is in the \(xy\)-plane with radius \(3\) and center at the origin.

      The plot shows a donut (or torus) of radius 2 whose central circle is in the xy-plane with radius 3 and center at the origin.
  25. Plot each surface given in spherical coordinates, \((\rho,\phi,\theta)\) for \(0 \lt \phi \lt \pi\). Notice there is no \(\theta\) in the equation. So the shape is obtained by rotating a curve about the \(z\)-axis. Identify the shape of the surface.

    1. \(\rho=\phi\)

      What is this shape in the \(zr\)-plane with “polar” coordinates \((\rho,\phi)\)?

      Apple with stem on the positive \(z\)-axis
      and point on the negative \(z\)-axis.

      The plot shows the shape of an apple whose stem would come out along the positive z-axis.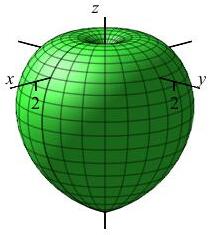

      First think about regular polar coordinates. In the \(xy\)-plane with polar coordinates \((r,\theta)\), the equation \(r=\theta\) is a spiral. Since \(\theta\) is measured from the positive \(x\)-axis the spiral starts at the positive \(x\)-axis.

      The plot shows a spiral going counterclockwise starting from the positive x axis and stopping at the negative x axis.
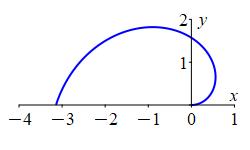      Analogously, in the \(zr\)-plane for any fixed \(\theta\) using \((\rho,\phi)\) as “polar” coordinates, the equation \(\rho=\phi\) is a spiral. Since \(\phi\) is measured from the positive \(z\)-axis the spiral starts at the positive \(z\)-axis.
      The plot shows a spiral going clockwise starting from the positive z-axis.
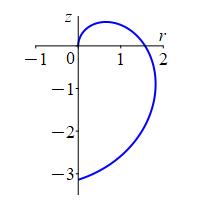      Since this is true for all \(\theta\), we rotate about the \(z\)-axis. The spiral sweeps out the shape of an apple whose stem would come out along the positive \(z\)-axis and has a point on the negative \(z\)-axis.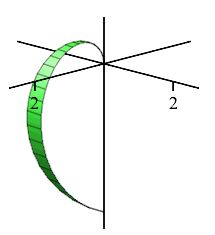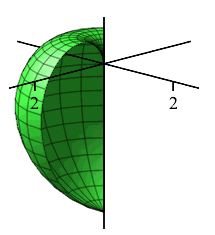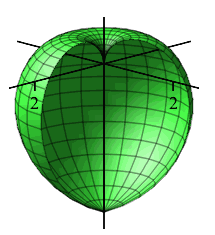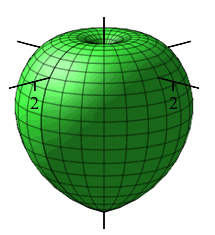
      The plot shows a spiral sweeping out the shape of an apple whose stem would come out along the positive z-axis and has a point on the bottom.

    2. \(\rho=1-\cos\phi\)

      What is this shape in the \(zr\)-plane with “polar” coordinates \((\rho,\phi)\)?

      Apple with stem on the positive \(z\)-axis
      and flat on the negative \(z\)-axis.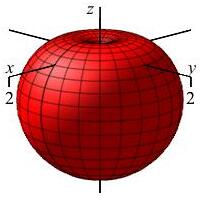

      The plot shows the shape of an apple whose stem would come out along the positive z-axis and is flat on the bottom.

      In regular polar coordinates \((r,\theta)\) in the \(xy\)-plane, the equation \(r=1-\cos\theta\) is a cardioid which starts on the positive \(x\)-axis.

      The plot shows half a cardioid going counterclockwise starting from the positive x axis and ending at negative x axis.

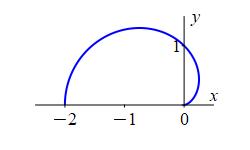
      Analogously, in the \(zr\)-plane for any fixed \(\theta\) using \((\rho,\phi)\) as “polar” coordinates, the equation \(\rho=1-\cos\phi\) is a cardioid which starts on the positive \(z\)-axis.

      The plot shows half a cardioid going clockwise starting from the positive z axis and ending at the negative z axis.
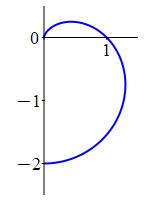      When we rotate about the \(z\)-axis, the cardioid sweeps out an apple whose stem comes out along the positive \(z\)-axis but is flat on the negative \(z\)-axis.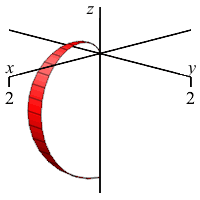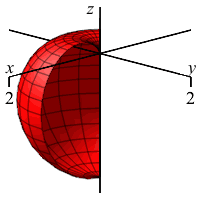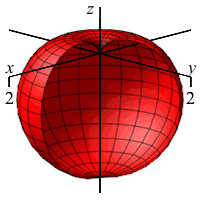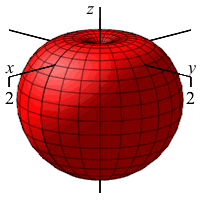
      The plot shows a cardioid sweeping out the shape of an apple whose stem would come out along the positive z-axis and is flat on the bottom.

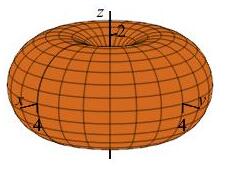
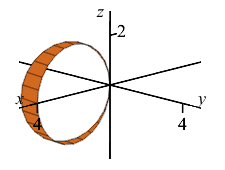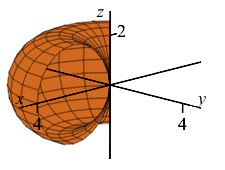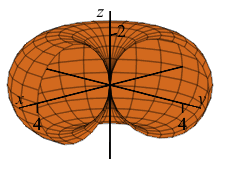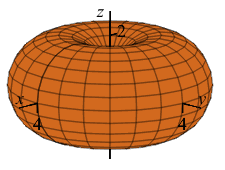
    3. \(\rho=4\sin\phi\)

      What is this shape in the \(zr\)-plane with “polar” coordinates \((\rho,\phi)\)?

      Donut (torus) without hole centered at the origin whose central circle is in the \(xy\)-plane and has radius \(2\).

      The plot shows a donut (torus) whose hole has shrunk to a point centered at the origin whose central circle in in the xy-plane with radius 2.

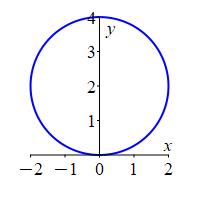
      In regular polar coordinates \((r,\theta)\) in the \(xy\)-plane, the equation \(r=4\sin\theta\) is a circle of radius \(2\) centered at \((x,y)=(0,2)\).

      The plot shows a circle with radius 2 centered at 0,2 in the x y plane.

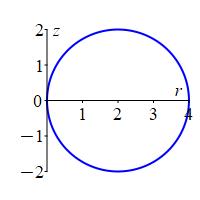
      Analogously, in the \(zr\)-plane for any fixed \(\theta\) using \((\rho,\phi)\) as “polar” coordinates, the equation \(\rho=4\sin\phi\) is a circle of radius \(2\) centered at \((z,r)=(0,2)\).

      The plot shows a circle with radius 2 centered at 2,0.

      When we rotate about the \(z\)-axis, the circle sweeps out a donut (torus) without hole centered at the origin whose central circle is in the \(xy\)-plane and has radius \(2\). Since the two radii are equal, there is no hole in the donut.

      The plot shows a donut (torus) whose hole has shrunk to a point centered at the origin whose central circle in in the xy-plane with radius 2.

    4. \(\rho=4\cos\phi\)

      What is this shape in the \(zr\)-plane with “polar” coordinates \((\rho,\phi)\)?

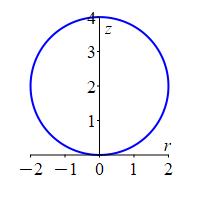
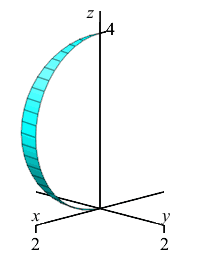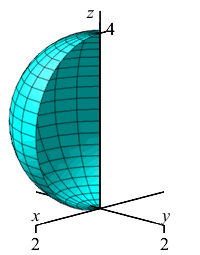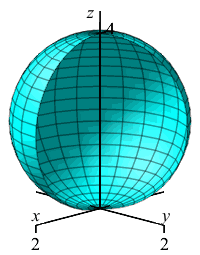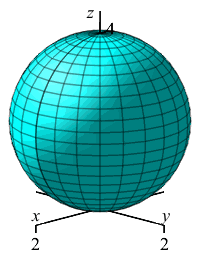
      Sphere of radius \(2\) centered at \((x,y,z)=(0,0,2)\).

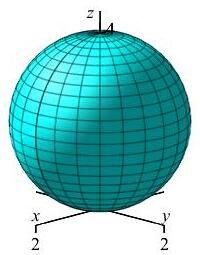
      The plot shows a sphere with radius 2 centered at 0,0,2.

      In regular polar coordinates \((r,\theta)\) in the \(xy\)-plane, the equation \(r=4\cos\theta\) is a circle of radius \(2\) centered at \((x,y)=(2,0)\).

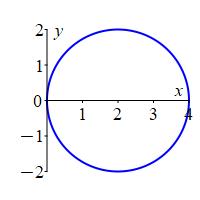
      The plot shows a circle with radius 2 centered at 2,0 in the x y plane.

      Analogously, in the \(zr\)-plane for any fixed \(\theta\) using \((\rho,\phi)\) as “polar” coordinates, the equation \(\rho=4\cos\phi\) is a circle of radius \(2\) centered at \((z,r)=(2,0)\).

      The plot shows a circle with radius 2 centered at 0,2.

      When we rotate about the \(z\)-axis, the circle sweeps out a sphere of radius \(2\) centered at \((x,y,z)=(0,0,2)\).

      The video shows the circle of the previous plot rotating about the z axis and sweeping out a sphere with radius 2 centered at 0,0,2.

    26. Review Exercises

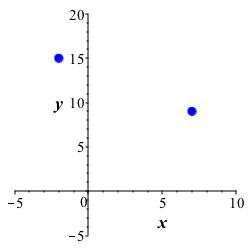
  26. Graph the points \((-2,15)\) and \((7,9)\) and find the distance between.

    \(d=3\sqrt{13}\)

    The graph of the points is shown.

    We find the distance by \[\begin{aligned} d&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \\ &=\sqrt{(7-(-2))^2+(9-15)^2} \\ &=\sqrt{(9)^2+(-6)^2} \\ &=\sqrt{117} =3\sqrt{13} \end{aligned}\]

    The plot shows 2 points at -2,15 and 7,9.

  27. Consider the polar coordinates \((r,\theta)=\left(5,\dfrac{3\pi}{2}\right)\).

    1. Convert the point into rectangular coordinates \((x,y)\).

      \((0,-5)\)

      To convert to rectangular coordinates, we compute: \[\begin{aligned} x&=r\cos\theta=5\cos\left(\dfrac{3\pi}{2}\right)=0 \\ y&=r\sin\theta=5\sin\left(\dfrac{3\pi}{2}\right)=-5 \end{aligned}\] So the rectangular coordinates are: \[ (x,y)=\left(0,-5\right) \]

    2. Find the distance between that point and the point \((10,0)\).

      \(d=5\sqrt{5}\)

      \(d=\sqrt{\Delta x^2+\Delta y^2}=\sqrt{10^2+(-5)^2}=\sqrt{125}=5\sqrt{5}\)

    3. Graph and calculate the perimeter of the triangle formed from the two previous points and the point \((5,2)\).

      \(d_\text{perimeter}=5\sqrt{5}+\sqrt{29}+\sqrt{74}\approx 25.2\)

      The three points are: \[ (0,-5), (10,0)\,\text{and}\,(5,2) \] Plotted below is the triangle

      x27c

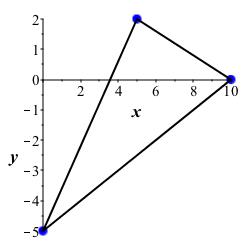
      The distance between the first two is \(d_1=5\sqrt{5}\). The distance between the last two is \[d_2=\sqrt{5^2+(-2)^2}=\sqrt{29}\] and the distance between the first and the last points is \[d_3=\sqrt{5^2+7^2}=\sqrt{25+49}=\sqrt{74}\] so the total distance around the perimeter is \[d_\text{perimeter}=d_1+d_2+d_3=5\sqrt{5}+\sqrt{29}+\sqrt{74}\approx 25.2\]

  28. Calculate the perimeter of the triangle formed by the three points \(A=(1,0,-3)\), \(B=(4,6,2)\), and \(C=(0,3,3)\).

    \(d_\text{perimeter}=\sqrt{70}+\sqrt{46}+\sqrt{26}\approx20. 25\)

    The distance between each pair of points is: \[\begin{aligned} d(A,B)=\sqrt{3^2+6^2+5^2}=\sqrt{70} \\ d(A,C)=\sqrt{(-1)^2+3^2+6^2}=\sqrt{46} \\ d(B,C)=\sqrt{4^2+3^2+(-1)^2}=\sqrt{26} \end{aligned}\] So the perimeter is \[ d_\text{perimeter} =\sqrt{70}+\sqrt{46}+\sqrt{26}\approx20.25 \]

  29. Convert the vertices of the triangle in the previous problem to cylindrical and spherical coordinates

    Point \(A=(1,0,-3)\):
     Cylindrical: \((r,\theta,z)=(1,0,-3)\)
     Spherical: \((\rho,\phi,\theta) =\left(\sqrt{10},\arccos \dfrac{-3}{\sqrt{10}},0\right)\)
    Point \(B=(4,6,2)\):
     Cylindrical \((r,\theta,z)=\left(\sqrt{52},\arctan\dfrac{3}{2},2\right)\)
     Spherical \((\rho,\phi,\theta) =\left(\sqrt{56},\arccos\dfrac{2}{\sqrt{56}},\arctan\dfrac{3}{2}\right)\)
    Point \(C=(0,3,3)\):
     Cylindrical \((r,\theta,z)=\left(3,\dfrac{\pi}{2},3\right)\)
     Spherical \((\rho,\phi,\theta) =\left(3\sqrt{2},\dfrac{\pi}{4},\dfrac{\pi}{2}\right)\)

    Point \(A=(1,0,-3)\): \[\begin{aligned} r&=\sqrt{x^2+y^2}=\sqrt{1^2+0^2}=1 \\ \theta&=\arctan\dfrac{y}{x}=\arctan0=0 \\ \rho&=\sqrt{x^2+y^2+z^2}=\sqrt{1^2+0^2+(-3)^2}=\sqrt{10} \\ \phi&=\arccos\dfrac{z}{\rho}=\arccos \dfrac{-3}{\sqrt{10}} \end{aligned}\] Cylindrical: \((r,\theta,z)=(1,0,-3)\)
    Spherical: \((\rho,\phi,\theta) =\left(\sqrt{10},\arccos \dfrac{-3}{\sqrt{10}},0\right)\)

    Point \(B=(4,6,2)\): \[\begin{aligned} r&=\sqrt{4^2+6^2}=\sqrt{52} \\ \theta&=\arctan\dfrac{6}{4}=\arctan\dfrac{3}{2} \\ \rho&=\sqrt{x^2+y^2+z^2}=\sqrt{4^2+6^2+2^2}=\sqrt{56} \\ \phi&=\arccos\dfrac{z}{\rho}=\arccos\dfrac{2}{\sqrt{56}} \end{aligned}\] Cylindrical \((r,\theta,z)=\left(\sqrt{52},\arctan\dfrac{3}{2},2\right)\)
    Spherical \((\rho,\phi,\theta) =\left(\sqrt{56},\arccos\dfrac{2}{\sqrt{56}},\arctan\dfrac{3}{2}\right)\)

    Point \(C=(0,3,3)\): \[\begin{aligned} r&=\sqrt{0^2+3^2}=3 \\ \theta&=\dfrac{\pi}{2} \text{ because on } y\text{-axis} \\ \rho&=\sqrt{0^2+3^2+3^2}=\sqrt{18}=3\sqrt{2} \\ \phi&=\arccos\dfrac{z}{\rho}=\arccos\dfrac{3}{3\sqrt{2}}=\dfrac{\pi}{4} \end{aligned}\] Cylindrical \((r,\theta,z)=\left(3,\dfrac{\pi}{2},3\right)\)
    Spherical \((\rho,\phi,\theta) =\left(3\sqrt{2},\dfrac{\pi}{4},\dfrac{\pi}{2}\right)\)

  30. Convert \(r=4\sin\theta\) to rectangular coordinates and identify the curve

    When converted to rectangular coordinates, we have the equation \(x^2+(y-2)^2=4\). Thus the curve is a circle of radius \(2\) centered at \((0,2)\).

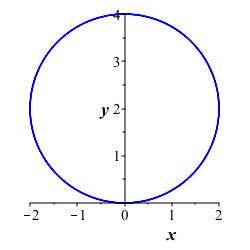
    The plot shows a circle centered at 0,2 with radius 2.

    Multiply both sides of \(r=4\sin\theta\) by \(r\) and substitute \(r^2=x^2+y^2\) and \(r\sin\theta=y\). Then complete the square on \(y\): \[\begin{aligned} r^2=4r\sin\theta \\ x^2+y^2=4y \\ x^2+(y-2)^2=4 \end{aligned}\] This is a circle of radius \(2\) centered at \((0,2)\).

    The plot shows a circle centered at 0,2 with radius 2.

© MY Math Apps

Supported in part by NSF Grant #1123255

NSF logo