1. Polar Coordinates
c. Polar Coordinates - 2D
3. Polar Equations
A rectangular equation is an equation which involves the rectangular coordinates, \(x\) and \(y\). For example, \(y=x^2\) and \(\left(x^2+y^2\right)^2=2xy\) are rectangular equations. A solution of a rectangular equation is a point \(P=(x,y)\) for which its coordinates \((x,y)\) satisfy the equation. For example, \((-2,4)\) is a solution of \(y=x^2\) and \((-2,-2)\) is a solution of \(\left(x^2+y^2\right)^2=2xy\).
A polar equation is an equation which involves the polar coordinates, \(r\) and \(\theta\). For example, \(r^2=1+r\sin 2\theta\) and \(r=-e^\theta\) are polar equations. A solution of a polar equation is a point \(P=(r,\theta)\) for which some pair of coordinates \((r,\theta)\) satisfy the equation. For example, \(P=(1,\pi)\) is a solution of \(r^2=1+r\sin 2\theta\). In addition, \(P=(1,\pi)\) is a solution of \(r=-e^\theta\) because we can also write \(P\) as \(P=(-1,0)\) and \((-1,0)\) satisfies \(r=-e^\theta\). This is weird but true!
On this page, we discuss converting rectangular equations into polar equations and vice versa.
Rectangular to Polar
To convert a rectangular equation into a polar equation, simply substitute \(x=r\cos\theta\) and \(y=r\sin\theta\) and simplify. As a shortcut, you may use the identity \(x^2+y^2=r^2\). You may also cancel factors of \(r\) provided the origin remains a solution.
Convert the rectangular equation \(\left(x^2+y^2\right)^2=2xy\) to polar form.
Substitute \(x=r\cos\theta\) and \(y=r\sin\theta\) and simplify: \[\begin{aligned} \left(x^2+y^2\right)^2&=2xy \\ \left(r^2\right)^2&=2(r\cos\theta)(r\sin\theta) \\ r^4&=2r^2\sin\theta\cos\theta \\ r^2&=2\sin\theta\cos\theta \end{aligned}\] We can cancel the \(r^2\) because \((r,\theta) =(0,0)\) is still a solution. Finally, we use the identity \(\sin(2\theta)=2\sin\theta\cos\theta\) to conclude: \[ r^2=\sin(2\theta) \]
Obtain a polar equation for the hyperbola, \(x^2-y^2=1\).
\(r^2\cos 2\theta =1\)
or \(r^2=\sec 2\theta\)
or \(r=\pm\sqrt{\sec 2\theta }\)
\[\begin{aligned} x^2-y^2&=1 \\ (r\cos\theta)^2-(r\sin\theta)^2&=1 \\ r^2\left(\cos^2\theta-\sin^2\theta\right)&=1 \\ r^2\cos(2\theta)&=1 \end{aligned}\] We have used the identity \(\cos(2\theta)=\cos^2\theta-\sin^2\theta\). We can also rewrite the equation as \(r^2=\sec(2\theta)\) or \(r=\pm\sqrt{\sec(2\theta)}\).
Polar to Rectangular
To convert a polar equation into a rectangular equation, substitute \(\cos\theta=\dfrac{x}{r}\) and \(\sin\theta=\dfrac{y}{r}\) or if useful \(\tan\theta=\dfrac{y}{x}\). Then substitute \(r^2=x^2+y^2\).
Convert the polar equation \(r^2=\cos 2\theta\) to rectangular form.
First use the identity \(\cos(2\theta)=\cos^2\theta-\sin^2\theta\) to express everything in terms of \(\sin\theta\) and \(\cos\theta\): \[\begin{aligned} r^2&=\cos 2\theta \\ r^2&=\cos^2\theta-\sin^2\theta \\ r^2&=\left(\dfrac{x}{r}\right)^2-\left(\dfrac{y}{r}\right)^2 \end{aligned}\] Now clear the denominator: \[\begin{aligned} r^4&=x^2-y^2 \\ \left(x^2+y^2\right)^2&=x^2-y^2 \end{aligned}\]
Obtain a Cartesian equation for the polar equation, \(r=2\cos\theta\). Identify the graph by looking at the rectangular equation.
To identfy the graph, first complete the square.
\(x^2+y^2=2x\)
or \((x-1)^2+y^2=1\)
Circle of radius \(1\) centered at \((1,0)\).
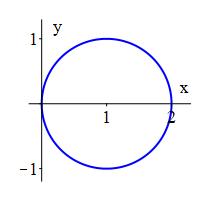
\[\begin{aligned} r&=2\cos\theta \\ r&=2\dfrac{x}{r} \\ r^2&=2x \\ x^2+y^2&=2x \end{aligned}\] To identify the graph, we first complete the square by adding \(-2x+1\) to both sides: \[\begin{aligned} x^2-2x+1+y^2&=1 \\ (x-1)^2+y^2&=1 \end{aligned}\]
This is a circle of radius \(1\) centered at \((1,0)\).

Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum