1. Coordinate Systems
a. Rectangular Coordinates - 2D, 3D and nD
3. Rectangular Coordinates in Higher Dimensions (Optional)
The ideas of \(2\) dimensional space (a plane, \(\mathbb{R}^2\)) and \(3\) dimensional space (\(\mathbb{R}^3\)) can be generalized to any number of dimensions although we cannot actually visualize it. A point \(P\) in \(n\)-dimensional space is specified by giving an ordered \(n\) -tuple such as \(P=(p_1,p_2,\cdots,p_n)\). Since it takes \(n\) real numbers to specify a point, \(n\)-dimensional space is also called \(\mathbb{R}^n\). The origin is the point \((0,0,\cdots,0)\) and there are \(n\) axes, one for each coordinate, \(x_i\). The \(x_i\)-axis is the set of points of the form \((0,0,\cdots,x_i,\cdots,0)\).
In \(\mathbb{R}^4\), we take the coordinates as \((x,y,z,w)\). We think of \(x\), \(y\) and \(z\) as horizontal and \(w\) as vertical. The figure shows a hypercube in \(\mathbb{R}^4\) whose base is a cube (shown in red) in the horizontal \(xyz\)-hyperplane.
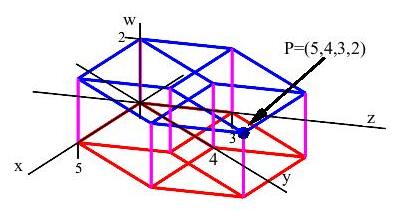
by Avek Dongol
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum