1. Coordinate Systems

a. Rectangular Coordinates - 2D, 3D and nD

1. 2D Rectangular Coordinates

The Rectangular Coordinate System in the plane (also called the Cartesian Coordinate System after its creator, Rene Descartes) is a method of uniquely identifying points in a plane by giving two numbers. A grid is drawn with a pair of lines (axes) drawn perpendicular to each other. The horizontal axis is called the \(x\)-axis, and the vertical axis is called the \(y\)-axis. The point at which the axes intersect is called the origin, \(O\). The axes are marked off in unit lengths that can be used to locate points in the \(xy\)-plane. Each point in the plane is specified by giving an ordered pair \((x,y)\). The first number is the \(x\)-coordinate (its horizontal position on the \(x\)-axis) and the second number is the \(y\)-coordinate (its vertical position on the \(y\)-axis). \(x\)-coordinates are positive to the right of the origin and negative to the left. \(y\)-coordinates are positive above the origin and negative below. Since it takes \(2\) \(\mathbb{R}\)eal numbers to specify a point, the plane is also called \(\mathbb{R}^2\). In the plot, we have marked in the point \(P=(4,3)\):

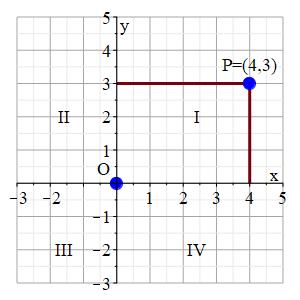
The plot shows a square grid with a vertical line labeled as the y axis
and a horizontal line labeled as the x axis. Tick marks next to
the y axis are labeled upward with numbers increasing from 1, and downward
decrease from -1. Tick marks below the x axis are
labeled to the right with numbers increasing from 1, and to the left with
numbers decreasing from -1. The intersection of the x and y
axes is labeled O. The area above the x axis and to the right of the y axis
is labeled I and is called the first quadrant. The area above the x axis
and to the left of the y axis is labeled II and named the second quadrant.
The area below the x axis and to the left of the y axis is labeled III and
callthe third quadrant. Finally, the area below the x axis and to the right
of the y axis is labeled IV and named the fourth quadrant.
In the quadrant I, a point 4 to the right and 3 up is
labeled P=(4,3) and has line segments from the point to the tick mark 4 on
the x-axis and 3 on the y-axis.

The intersecting axes create four Quadrants, labeled I, II, III and IV counterclockwise starting from the top right as shown above. The table shows which coordinates are positive or negative in each quadrant.

Quadrant:	I	II	III	IV
\(x\)	\(+\)	\(-\)	\(-\)	\(+\)
\(y\)	\(+\)	\(+\)	\(-\)	\(-\)

When working with symbols, the coordinates of a point are frequently written using subscripts. Thus a point \(P\) may be written as \(P=(p_1,p_2)\).

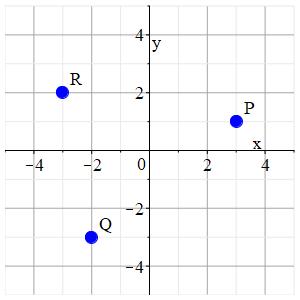
Identify the coordinates of each point in the plot:

\(P=\)	\((1,3)\)	\((3,1)\)	\((-3,1)\)	\((1,-3)\)
\(Q=\)	\((-2,-4)\)	\((-3,-2)\)	\((-2,-3)\)	\((-2,3)\)
\(R=\)	\((-3,2)\)	\((3,-2)\)	\((2,-3)\)	\((2,-3)\)

The plot shows three points in the plane.
A point P is above 3 on the x axis and to the right 1 on the y axis.
A point Q is below -2 on the x axis and to the left of -3 on the y axis.
A point R is above -3 on the x axis and to the left of 2 on the y axis.

1. Coordinate Systems

a. Rectangular Coordinates - 2D, 3D and nD

1. 2D Rectangular Coordinates

Heading