6. Volume
Exercises
-
The base of a solid is the circle \(x^2+y^2=9\). Find its volume if the cross-sections perpendicular to the \(x\)-axis are:
-
squares
\(V=144\)
The line segment on the base (shown in the figure) perpendicular to the \(x\)-axis has endpoints \(y_+=+\sqrt{9-x^2}\) and \(y_-=-\sqrt{9-x^2}\).
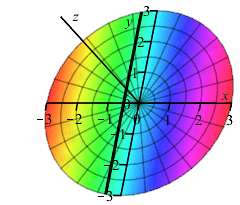
Therefore, the length of the side of the square cross-section, shown in the figure, is \(s=y_+-y_-=2\sqrt{9-x^2}\). Hence, the cross-sectional area is: \[ A=s^2=4(9-x^2) \]
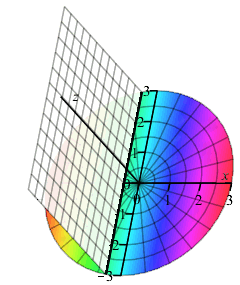
To find the volume, we integrate the area from the leftmost extreme of the circle to the rightmost extreme (values of \(x\) for which \(y=0\)). This gives us the limits \(x=-3\) to \(x=3\). A visualization of the integration is shown in the animation. \[\begin{aligned} V&=\int_{-3}^3 A(x)\,dx =4\int_{-3}^3 9-x^2\,dx\\ &=4\left[9x-\dfrac{x^3}{3}\right]_{-3}^3=144 \end{aligned}\]
ar,lk
-
semi-circles
\(V=18\pi\)
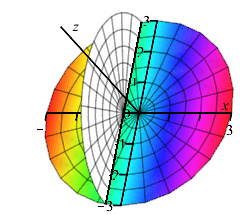
Similar to the previous part, the line segment on the base (shown in the figure) perpendicular to the \(x\)-axis has endpoints \(y_+=+\sqrt{9-x^2}\) and \(y_-=-\sqrt{9-x^2}\).

The radius of the semi-circular cross-section (shown in the figure) is \(r=|y_\pm|=\sqrt{9-x^2}\). So the cross-sectional area is: \[ A=\dfrac{1}{2}\pi\left(\sqrt{9-x^2}\right)^2 =\dfrac{1}{2}\pi(9-x^2) \]
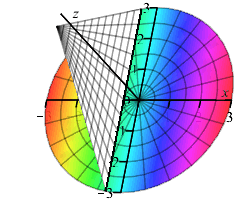
Integrating the area from \(x=-3\) to \(x=3\) gives us the volume. A visualization of the integration is shown in the animation. \[\begin{aligned} V &=\int_{-3}^3 A(x)\,dx =\dfrac{1}{2}\pi\int_{-3}^3 (9-x^2)\,dx\\ &=\dfrac{1}{2}\pi\left[9x-\dfrac{x^3}{3} \right]_{-3}^3=18\pi \end{aligned}\]
ar,lk
The resulting solid is a hemisphere, with radius \(3\). So the volume is \(\dfrac{1}{2}\left(\dfrac{4}{3}\pi r^3\right)=18\pi\) cubic units. This verifies our integration.
-
equilateral triangles
\(V=36 \sqrt3\)
Similar to the previous two parts, the line segment on the base (shown in the figure) perpendicular to the \(x\)-axis has endpoints \(y_+=+\sqrt{9-x^2}\) and \(y_-=-\sqrt{9-x^2}\).

The base of the triangular cross-section (shown in the figure) is \(b=y_+-y_-=2\sqrt{9-x^2}\). The height of the cross-section is \(h=\dfrac{b}{2}\tan 60^{\circ}=\sqrt3\sqrt{9-x^2}\). So the cross-sectional area is: \[\begin{aligned} A &=\dfrac{1}{2}bh =\dfrac{1}{2}(2\sqrt{9-x^2})(\sqrt3\sqrt{9-x^2})\\ &=\sqrt3(9-x^2) \end{aligned}\]
Integrating the area from \(x=-3\) to \(x=3\) gives us the volume. A visualization of the integration is shown in the animation. \[\begin{aligned} V &=\int_{-3}^3 A(x)\,dx =\sqrt3\int_{-3}^3 (9-x^2)\,dx\\ &=\sqrt3\left[9x-\dfrac{x^3}{3}\right]_{-3}^3=36\sqrt3 \end{aligned}\]
ar,lk
PY: Alt Text checked to here.
-
-
The base of a solid is the region between \(y=2x-x^2\) and \(2y+x=2\). The cross-sections perpendicular to the \(x\)-axis are isosceles right triangles with one leg in the base of the solid. Set up the integral for volume. Use a calculator to evaluate it.
(The algebra is easy but tedious!)In an isosceles right triangle the two legs have equal length giving \(A=\dfrac12 l^2\), where \(l\) is the length of the leg.
\(\displaystyle V =\dfrac{1}{2}\int_{1/2}^2 \left(\dfrac {5x}{2}-x^2-1\right)^2\,dx =\dfrac{81}{640}\approx 0.126\,56\)
Here is a figure of the base. The line segment on the base perpendicular to the \(x\)-axis has endpoints \(y_\text{upper}=2x-x^2\) and \(y_\text{lower}=1-\dfrac x2\)
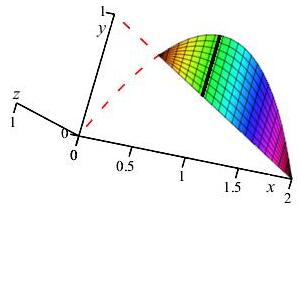
The base of the triangular cross-section (shown in the figure) is \(b=y_\text{upper}-y_\text{lower}=\dfrac {5x}{2}-x^2-1 \). It is given that the height is also equal to the base: \(h=b=\dfrac {5x}{2}-x^2-1\). So the cross-sectional area is: \[ A=\dfrac{1}{2}bh =\dfrac{1}{2}\left(\dfrac {5x}{2}-x^2-1\right)^2 \]
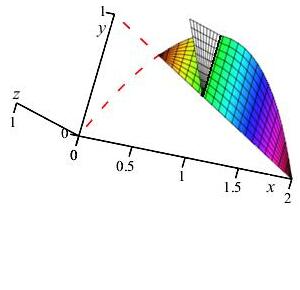
To obtain the volume, we must integrate the area across the base. To find the limits of integration, we need the points of intersection of the line and the parabola: \(2x-x^2=1-\dfrac{x}{2}\). Simplifying this equation gives us \((2x-1)(x-2)=0\). Therefore, the limits are from \(x=\dfrac{1}{2}\) to \(x=2\).
The volume is: \[\begin{aligned} V&=\int_{1/2}^2 A(x)\,dx =\int_{1/2}^2 \dfrac {1}{2}\left(\dfrac {5x}{2}-x^2-1\right)^2\,dx \\ &=\dfrac{81}{640}\approx 0.126\,56 \end{aligned}\]
ar
-
The base of a solid is the region bounded by \(y=e^x\), \(x=0\) and \(y=e\). The cross-sections perpendicular to the \(y\)-axis are rectangles whose height is equal to half of its base. Find the volume.
You must solve \(y=e^{x}\) for \(x\)! Then use integration by parts
\(V=\dfrac{e}{2}-1\)
Since the cross-sections are perpendicular to the \(y\)-axis, we write the boundaries as functions of \(y\). So the segment on the base, perpendicular to the \(y\)-axis, has endpoints \(x_\text{left}=0\) and \(x_\text{right}=\ln y\). They intersect at \(y=1\) and the region is cut off at \(y=e\).
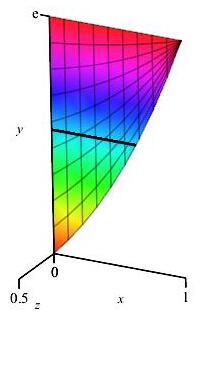
The base of the rectangular cross-section (shown in the figure) is \(b=x_\text{right}-x_\text{left}=\ln y-0=\ln y \). The height of the rectangle is half of its base: \(h=\dfrac b2=\dfrac {\ln y}{2}\). So the cross-sectional area is: \[ A=bh=(\ln y)\left(\dfrac{\ln y}{2}\right)=\dfrac12(\ln y)^2 \] To find the volume we integrate the area from \(y=1\) to \(y=e\): \[ V=\int_1^e A(y)\,dy=\int_1^e \dfrac 12(\ln y)^2\,dy \]
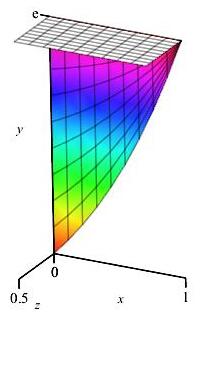
The animation here represents the integration of the area.
We apply integration by parts with: \[\begin{array}{ll} u=(\ln y)^2 & dv=\dfrac12\,dy \\ du=\dfrac{2\ln y}{y}\,dy \quad & v=\dfrac{y}{2} \end{array}\] So the indefinite integral is: \[\begin{aligned} \int \dfrac12(\ln y)^2\,dy &=(\ln y)^2\dfrac{y}{2}- \int \left(\dfrac y2\right)\left(\dfrac{2\ln y}{y}\right)\,dy \\ &=(\ln y)^2\dfrac{y}{2}- \int \ln y\,dy \\ &=(\ln y)^2\dfrac{y}{2}-(y\ln y-y)+C \end{aligned}\]Finally the volume is: \[\begin{aligned} V &=\int_1^e \dfrac 12(\ln y)^2\,dy =\left[(\ln y)^2\dfrac{y}{2}-(y\ln y-y)\right]_1^e \\ &=\dfrac{e}{2}-1 \end{aligned}\]
ar
-
\(y=\cos x\) and \(y=0\) for \(0 \le x \le \dfrac{\pi}{2}\) about the \(x\)-axis
\(x\)-integral, vertical rectangles, disk
Since \(y\) is given as functions of \(x\), we compute an \(x\)-integral. So the slices are vertical as shown in the figure.
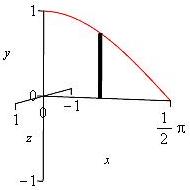
The slices revolve into disks.
ar,py
-
\(x=\sqrt{y}\) and \(x=3\) between \(y=0\) and \(y=4\) about the:
-
\(y\)-axis.
\(y\)-integral, horizontal rectangles, washer
Since \(x\) is given as a function of \(y\), we use a \(y\)-integral. So the slices are horizontal as shown.
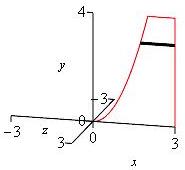
Rotating the slices about the \(y\)-axis gives washers as shown.
ar,py
-
\(x=-1\)
\(y\)-integral, horizontal rectangles, washer
Similar to the previous part, we do a \(y\)-integral. So there are horizontal slices.
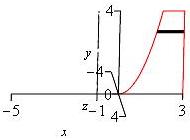
This time the axis of rotation is \(x=-1\) as shown. The horizontal slice still rotates into a washer.
ar,py
-
-
\(y=x^2\), \(\,y=0\) and \(x=3\) about \(y\)-axis.
\(x\)-integral, vertical rectangles, cylinder
Here \(y\) is a function of \(x\), so we use an \(x\)-integral, with vertical slices. The diagram shows one highlighted vertical slice.
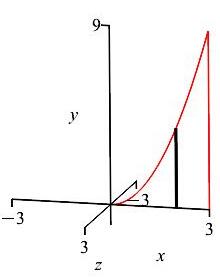
When the vertical slices are rotated about the \(y\)-axis we get thin cylinders.
-
\(x=y^2\), \(\,y=0\) and \(x=16\) about \(x\)-axis
\(y\)-integral, horizontal rectangles, cylinder
Since \(x\) is a function of \(y\), we shall use a \(y\)-integral, with horizontal slices. The diagram shows one highlighted horizontal slice.
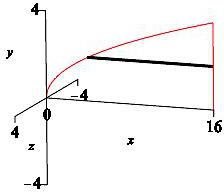
When the horizontal slices are rotated about the \(x\)-axis we get thin cylinders.
ar
-
\(y=x^2\), \(y=0\) and \(x=3\) about the
-
\(x\)-axis
\(x\)-integral, vertical rectangles, disk
Since \(y\) is given as a function of \(x\), we do an \(x\)-integral. The slices are vertical as shown.
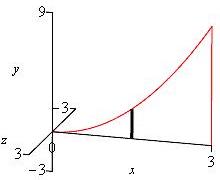
Rotating the slices about the \(x\)-axis, gives disks, not washers. (See the animation.)
ar,py
-
\(y=-1\)
\(x\)-integral, vertical rectangles, washer
Similar to part (a), we do an \(x\)-integral with vertical slices. However, in this case the axis of rotation is \(y=-1\) as shown in the diagram.
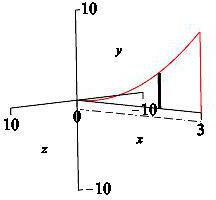
Rotating the vertical slices about the line \(y=-1\), gives us washers (see the animation).
ar,py
-
-
\(x=\dfrac{1}{\sqrt{y}}\) and the \(y\)-axis for \(4 \le y \le 8\) about the \(y\)-axis
\(y\)-integral, horizontal rectangles, disk
Since \(x\) is given as a function of \(y\), we do a \(y\)-integral. So the slices are horizontal as shown in the figure.
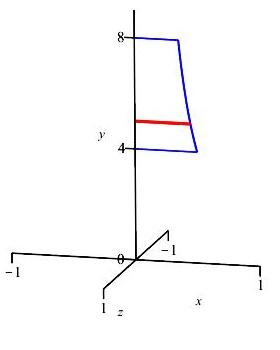
The slices revolve into disks.
py
-
\(y=x^2+2\),\(\quad y=0\),\(\quad x=0\) and \(x=3\) about \(x=4\)
\(x\)-integral, vertical rectangles, cylinder
Here \(y\) is a function of \(x\), so we use an \(x\)-integral. with vertical slices. The diagram shows the region, one highlighted vertical slice and the axis of rotation.
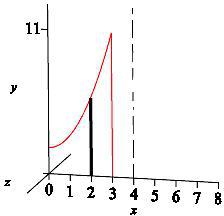
When these vertical slices are rotated about the line \(x=4\), we get thin cylinders.
ar
-
\(x=y^{3/2}\) and the \(y\)-axis for \(2 \le y \le 4\) about the \(y\)-axis
\(y\)-integral, horizontal rectangles, disk
Since \(x\) is given as a function of \(y\), we do a \(y\)-integral. So the slices are horizontal as shown in the figure.
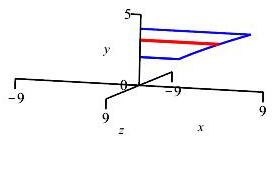
The slices revolve into disks.
py
-
\(y=e^{-x^2}\), \(y=0\), \(x=0\), and \(x=1\) about \(y\)-axis
\(x\)-integral, vertical rectangles, cylinder
Since \(y\) is a function of \(x\), we shall use an \(x\)-integral, with vertical slices. The diagram shows the region and one highlighted vertical slice.
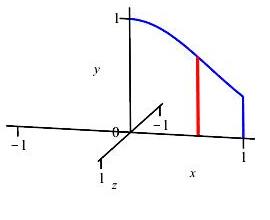
When these vertical slices are rotated about the \(y\)-axis they produce thin cylinders.
ar
-
\(y=\sec x\) and the \(x\)-axis for \(-\,\dfrac{\pi}{4} \le x \le \dfrac{\pi}{4}\) about the \(x\)-axis
\(x\)-integral, vertical rectangles, disk
Since \(y\) is given as a function of \(x\), we compute an \(x\)-integral. So the slices are vertical.
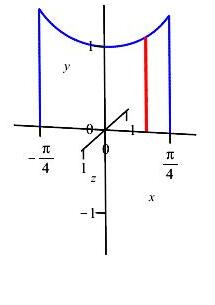
The slices revolve into disks.
py
-
\(y=3+x^2\) and \(y=4\) about \(x\)-axis
\(x\)-integral, vertical rectangles, washer
Here \(y\) is given as functions of \(x\). So we use an \(x\)-integral. Then the slices are vertical as shown.
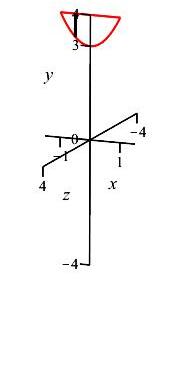
Rotating these slices about the \(x\)-axis gives washers.
ar,py,lk
-
\(x=\dfrac{y^2}{4a}\) (for \(a>0\)), \(\,y=0\) and \(x=a\) about the: (use \(y\)-integrals)
-
\(y\)-axis
\(y\)-integral, horizontal rectangles, washer
We are told to use \(y\)-integrals. So the slices are horizontal as shown in the diagram.
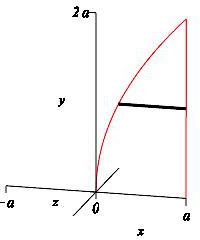
When the horizontal slices are rotated about the \(y\)-axis, they produce washers as observed in the animation.
ar,py
-
\(x=a\)
\(y\)-integral, horizontal rectangles, disk
As in the previous part, we use \(y\)-integrals where the slices are horizontal as shown in the diagram. Note that in this case the axis of rotation is \(x=a\).
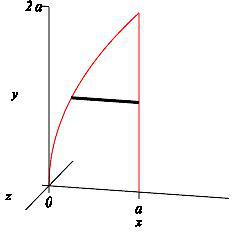
When the horizontal slices are rotated about the line \(x=a\), they produce disks, not washers as observed in the animation.
ar,py
-
\(x=2a\)
\(y\)-integral, horizontal rectangles, washer
Once again, we use \(y\)-integrals where the slices are horizontal. In this case the axis of rotation is \(x=2a\) as shown in the diagram.
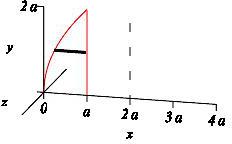
When the horizontal slices are rotated about the line \(x=2a\), they produce washers (see the animation).
ar,py
-
-
\(y=2\sqrt{ax}\) (for \(a>0\)), \( y=0\) and \(x=a\) about the: (use \(x\)-integrals)
-
\(y\)-axis
\(x\)-integral, vertical rectangles, cylinder
Since \(y\) is a function of \(x\), we use an \(x\)-integral, with vertical slices. The diagram shows the region and one highlighted vertical slice.
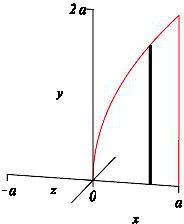
When these vertical slices are rotated about the \(y\)-axis we get thin cylinders.
This is the exact same volume as in part (a) of the previous exercise just calculated using thin cylinders instead of washers!
ar
-
\(x=a\)
\(x\)-integral, vertical rectangles, cylinder
Again, \(y\) is a function of \(x\), so we use an \(x\)-integral, with vertical slices. The diagram shows the region and one highlighted vertical slice.
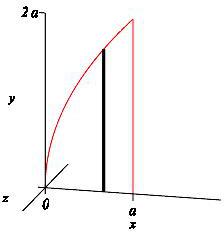
When these vertical slices are rotated about the line \(x=a\), we get thin cylinders.
This is the exact same volume as in part (b) of the previous exercise just calculated using thin cylinders instead of disks!
ar
-
\(x=2a\)
\(x\)-integral, vertical rectangles, cylinder
Once again, \(y\) is a function of \(x\), so we use an \(x\)-integral, with vertical slices. The diagram shows the region, one highlighted vertical slice and the axis of rotation.
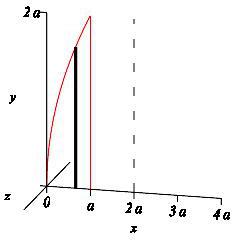
When these vertical slices are rotated about the line \(x=2a\), we get thin cylinders.
This is the exact same volume as in part (c) of the previous exercise just calculated using thin cylinders instead of washers!
ar
-
-
\(y=\cos x\) and \(y=0\) for \(0 \le x \le \dfrac{\pi}{2}\) about the \(x\)-axis
Remember the identity: \(\cos^2x=\dfrac{1+\cos2x}{2}\)
\(V=\dfrac{\pi^2}{4}\)
Since \(y\) is given as functions of \(x\), we compute an \(x\)-integral. So the slices are vertical as shown in the figure.

The slices revolve into disks with radius \(r=y=\cos x\). So the area of the disk is: \[ A=\pi r^2=\pi\cos^2x =\pi\left(\dfrac{1+\cos2x}{2}\right) \] (using the identity \(\cos^2x=\dfrac{1+\cos2x}{2}\)).
The limits of integration are \(x=0\) to \(x=\dfrac\pi2\). So the volume is: \[\begin{aligned} V &=\int_0^{\pi/2} A(x)\,dx =\pi\int_0^{\pi/2} \dfrac{1+\cos2x}{2}\,dx \\ &=\dfrac{\pi}{2}\left[ x+\dfrac{\sin 2x}{2} \right]_0^{\pi/2}=\dfrac{\pi^2}{4} \end{aligned}\]
ar
-
\(x=\dfrac{1}{\sqrt{y}}\) and the \(y\)-axis for \(4 \le y \le 8\) about the \(y\)-axis
\(V=\pi\ln2\)
Since \(x\) is given as a function of \(y\), we do a \(y\)-integral. So the slices are horizontal as shown in the figure.

The slices revolve into disks with radius \(r=x=\dfrac{1}{\sqrt{y}}\). So the area of the disk is: \[ A=\pi r^2=\dfrac{\pi}{y} \]
The limits of integration are \(y=4\) to \(y=8\). So the volume is: \[\begin{aligned} V &=\int_4^8 A(y)\,dy =\pi\int_4^8 \dfrac{1}{y}\,dy \\ &=\pi\left[\ln(y)\rule{0pt}{10pt}\right]_4^8 =\pi(\ln8-\ln4)=\pi\ln2 \end{aligned}\]
py,lk
-
\(x=y^{3/2}\) and the \(y\)-axis for \(2 \le y \le 4\) about the \(y\)-axis
\(V=60\pi\)
Since \(x\) is given as a function of \(y\), we do a \(y\)-integral. So the slices are horizontal as shown in the figure.

The slices revolve into disks with radius \(r=x=y^{3/2}\). So the area of the disk is: \[ A=\pi r^2=\pi y^3 \]
The limits of integration are \(y=2\) to \(y=4\). So the volume is: \[\begin{aligned} V &=\int_2^4 A(y)\,dy =\pi\int_2^4 y^3\,dy \\ &=\pi\left[\dfrac{y^4}{4}\right]_2^4 =\pi(4^3-4)=60\pi \end{aligned}\]
py,lk
-
\(y=\sec x\) and the \(x\)-axis for \(-\,\dfrac{\pi}{4} \le x \le \dfrac{\pi}{4}\) about the \(x\)-axis
\(V=2\pi\)
Since \(y\) is given as a function of \(x\), we compute an \(x\)-integral. So the slices are vertical.

The slices revolve into disks with radius \(r=y=\sec x\). So the area of the disk is: \[ A=\pi r^2=\pi\sec^2x \]
The limits of integration are \(x=-\,\dfrac{\pi}{4}\) to \(x=\dfrac{\pi}{4}\). So the volume is: \[\begin{aligned} V &=\int_{-\pi/4}^{\pi/4} A(x)\,dx =\pi\int_{-\pi/4}^{\pi/4} \sec^2x\,dx \\ &=\pi\left[\tan x\rule{0pt}{10pt}\right]_{-\pi/4}^{\pi/4} =\pi(1--1)=2\pi \end{aligned}\]
py,lk
-
\(y=3+x^2\) and \(y=4\) about \(x\)-axis
\(V=\dfrac{48\pi}{5}\)
Here \(y\) is given as functions of \(x\). So we will use an \(x\)-integral. Then the slices are vertical as shown.

Rotating these slices about the \(x\)-axis gives washers that have outer radii \(R=4\) and inner radii \(r=3+x^2\). So the area of the washers is: \[\begin{aligned} A &=\pi(R^2-r^2) =\pi(4^2-(3+x^2)^2) \\ &=\pi(16-(9+6x^2+x^4)) \\ &=\pi(7-6x^2-x^4) \end{aligned}\]
To find the limits of integration we need to solve for the points of intersection of the line \(y=4\) and the parabola \(y=3+x^2\): \[\begin{aligned} 3+x^2=4 \quad &\implies\quad x^2=1 \\ &\implies\quad x=\pm 1 \end{aligned}\] Integrating the area of washer from \(x=-1\) to \(x=1\) gives the volume:
\[\begin{aligned} V &=\int_{-1}^1 A(x)\,dx =\pi\int_{-1}^1 (7-6x^2-x^4)\,dx \\ &=\pi\left[ 7x-2x^3-\dfrac{x^{5}}{5}\right]_{-1}^1 \\ &=2\pi\left[ 7-2-\dfrac{1}{5}\right] =\dfrac{48\pi}{5} \end{aligned}\]
ar
-
\(x=\sqrt{y}\) and \(x=3\) between \(y=0\) and \(y=4\) about the:
-
\(y\)-axis.
Here is a plot of the area along with one highlighted slice.

\(V=28\pi\)
Since \(x\) is given as a function of \(y\), we use a \(y\)-integral. So the slices are horizontal as shown.

Rotating the slices about the \(y\)-axis gives washers as shown. The outer radius is \(R=3\) and the inner radii is \(r=\sqrt{y}\). So the area of the cross-section is: \[\begin{aligned} A &=\pi R^2-\pi r^2 =\pi3^2-\pi\left(\sqrt y\right)^2\\ &=\pi(9-y) \end{aligned}\]
Since the function is cut off by \(y=0\) on the bottom and \(y=4\) on the top, the limits of integration are from \(y=0\) to \(y=4\). Therefore, the volume is: \[\begin{aligned} V &=\int_0^4 A(y)\,dy =\int_0^4 \pi(9-y)\,dy\\ &=\pi\left[ 9y-\dfrac{y^2}{2}\right]_0^4 =28\pi \end{aligned}\]
ar
-
\(x=-1\)
Here is a plot of the area along with one highlighted slice.

\(V=\dfrac{124\pi}{3}\)
Similar to the previous part, we do a \(y\)-integral. However, this time the axis of rotation is \(x=-1\) as shown. The horizontal slice still rotates into a washer.

The washers have outer radii \(R=(3-(-1))=4\) and inner radii \(r=(\sqrt{y}-(-1))=\sqrt{y}+1\). So the area of the cross-section is: \[\begin{aligned} A &=\pi R^2-\pi r^2 =\pi4^2-\pi\left(\sqrt y+1\right)^2\\ &=\pi\left[16-\left(y+2\sqrt y+1\right)\right]\\ &=\pi(15-y-2\sqrt y) \end{aligned}\]
The limits remain the same as the previous part (\(y=0\) to \(y=4\)). Therefore, the volume is: \[\begin{aligned} V &=\int_0^4 A(y)\,dy =\int_0^4 \pi(15-y-2\sqrt y)\,dy\\ &=\pi\left[ 15y-\dfrac{y^2}{2}-2\cdot\dfrac{2}{3}(y)^{3/2}\right]_0^4 \\ &=\pi\left[ \left(15(4)-\dfrac{4^2}{2}-\dfrac{4}{3}(4)^{3/2}\right)-(0)\right]\\ &=\pi\left[ 60-8-\dfrac43\cdot8\right] =\dfrac{124\pi}{3} \end{aligned}\]
ar
-
-
\(y=x^2\), \(y=0\) and \(x=3\) about the
-
\(x\)-axis
Here is a plot of the region along with one slice.

\(V=\dfrac{243\pi}{5}\)
Since \(y\) is given as a function of \(x\), we do an \(x\)-integral. The slices are vertical as shown.

Rotating the slices about the \(x\)-axis, gives disks, not washers. (See the animation.) The radius is \(r=y=x^2\). So, the area of the disk is: \[ A=\pi r^2=\pi(x^2)^2=\pi x^4 \]
To find the volume, we integrate the area of the disk from from \(x=0\) to \(x=3\): \[\begin{aligned} V &=\int_0^3 A(x)\,dx =\int_0^3 \pi x^4\,dx\\ &=\pi\left[\dfrac{x^5}{5}\right]_0^3 =\dfrac{243\pi}{5} \end{aligned}\]
ar
-
\(y=-1\)
Here is a plot of the region with one slice as well as the axis of rotation.

\(V=\dfrac{333\pi}{5}\)
Similar to part (a), we do an \(x\)-integral with vertical slices. However, in this case the axis of rotation is \(y=-1\) as shown in the diagram.

Rotating the vertical slices about the line \(y=-1\), gives us washers (see animation) with outer radii \(R=x^2-(-1)=x^2+1\) and inner radii \(r=1\). The area of the washer is: \[\begin{aligned} A &=\pi R^2-\pi r^2\\ &=\pi(x^2+1)^2-\pi(1)^2\\ &=\pi(x^4+2x^2+1)-\pi\\ &=\pi(x^4+2x^2) \end{aligned}\]
To obtain the volume, we integrate the area of the washer from \(x=0\) to \(x=3\): \[\begin{aligned} V &=\int_0^3 A(x)\,dx =\int_0^3 \pi(x^4+2x^2)\,dx\\ &=\pi\left[\dfrac{x^5}{5}+2\dfrac{x^3}{3}\right]_0^3\\ &=\pi\left[\dfrac{3^5}{5}+2\dfrac{3^3}{3}-(0)\right] =\dfrac{333\pi}{5} \end{aligned}\]
ar
-
-
\(x=\dfrac{y^2}{4a}\) (for \(a>0\)), \(\,y=0\) and \(x=a\) about the: (use \(y\)-integrals)
-
\(y\)-axis
Here is a plot of the area along with one horizontal slice.

\(V=\dfrac{8}{5}\pi a^3\)
We are told to use \(y\)-integrals. So the slices are horizontal as shown in the diagram.

When the horizontal slices are rotated about the \(y\)-axis, they produce washers as observed in the animation. The washers have outer radii \(R=x=a\) and inner radii \(r=x=\dfrac{y^2}{4a}\). The area of the cross-section is: \[\begin{aligned} A&=\pi R^2-\pi r^2 =\pi a^2-\pi\left(\dfrac{y^2}{4a}\right)^2 \\ &=\pi\left(a^2-\dfrac{y^4}{16a^2}\right) \end{aligned}\]
The limits of integration are \(y=0\) and \(y(a)=\sqrt{4a(a)}=2a\) (Note: \(a>0\), so \(\sqrt{4a^2}=2a\)). Hence, the volume is: \[\begin{aligned} V &=\int_0^{2a} A(y)\,dy\\ &=\int_0^{2a} \pi\left(a^2-\dfrac{y^4}{16a^2}\right)\,dy\\ &=\pi\left[a^2 y-\dfrac{1}{16a^2}\dfrac{y^5}{5}\right]_0^{2a}\\ &=\pi\left(a^2 (2a)-\dfrac{1}{16a^2}\dfrac{(2a)^5}{5}\right)\\ &=\pi a^3 \left(2-\dfrac{2}{5}\right) =\dfrac{8}{5}\pi a^3 \end{aligned}\]
ar
-
\(x=a\)
Here is a plot of the area along with one horizontal slice. Note that the axis of rotation is \(x=a\).

\(V=\dfrac{16}{15}\pi a^3\)
As in the previous part, we use \(y\)-integrals where the slices are horizontal as shown in the diagram. Note that in this case the axis of rotation is \(x=a\).

When the horizontal slices are rotated about the line \(x=a\), they produce disks, not washers as observed in the animation, with radii \(r=a-x=a-\dfrac{y^2}{4a}\). The area of a cross-section is: \[\begin{aligned} A &=\pi r^2=\pi\left(a-\dfrac{y^2}{4a}\right)^2 \\ &=\pi\left(a^2-\dfrac{y^2}{2}+\dfrac{y^4}{16a^2} \right) \end{aligned}\]
The limits of integration are still \(y=0\) to \(y=2a\). Therefore, the volume is: \[\begin{aligned} V &=\int_0^{2a} A(y)\,dy\\ &=\pi\int_0^{2a} \left(a^2-\dfrac{y^2}{2}+\dfrac{y^4}{16a^2} \right)\,dy \\ &=\pi\left[ a^2y-\dfrac{y^3}{6}+\dfrac{y^5}{80a^2}\right]_0^{2a} \\ &=\pi\left(a^2(2a)-\dfrac{(2a)^3}{6}+\dfrac{(2a)^5}{80a^2}\right) \\ &=\pi\left(2a^3-\dfrac{4a^3}{3}+\dfrac{2a^3}{5}\right) =\dfrac{16}{15}\pi a^3 \end{aligned}\]
ar
-
\(x=2a\)
Here is a plot of the area along with one horizontal slice. Observe the axis of rotation and try to determine whether to use disks or washers.

\(V=\dfrac{56}{15}\pi a^3\)
Once again, we use \(y\)-integrals where the slices are horizontal. In this case the axis of rotation is \(x=2a\) as shown in the diagram.

When the horizontal slices are rotated about the line \(x=2a\), they produce washers (see the animation). They have outer radii \(R=2a-\dfrac{y^2}{4a}\) and inner radii \(r=2a-a=a\). So the area of a washer is: \[\begin{aligned} A &=\pi R^2-\pi r^2\\ &=\pi\left(2a-\dfrac{y^2}{4a}\right)^2-\pi(a)^2\\ &=\pi\left(4a^2-y^2+\dfrac{y^4}{16a^2}\right)-\pi a^2\\ &=\pi\left(3a^2-y^2+\dfrac{y^4}{16a^2}\right) \end{aligned}\]
The limits of integration are still from \(y=0\) to \(y=2a\). Therefore, the volume is: \[\begin{aligned} V &=\int_0^{2a} A(y)\,dy\\ &=\int_0^{2a} \pi\left(3a^2-y^2+\dfrac{y^4}{16a^2}\right)\,dy\\ &=\pi\left[3a^2y-\dfrac{y^3}{3}+\dfrac{y^5}{80a^2}\right]_0^{2a}\\ &=\pi\left(6a^3-\dfrac{8a^3}{3}+\dfrac{2a^3}{5}\right) =\dfrac{56}{15}\pi a^3 \end{aligned}\]
ar
-
-
\(y=x^2\), \(y=0\) and \(x=3\) about \(y\)-axis.
Use an \(x\)-integral and cylinders. Here is a plot of the region and one highlighted rectangle:

\(V=\dfrac{81\pi}{2}\)
Here \(y\) is a function of \(x\), so we use an \(x\)-integral, with vertical slices. The diagram shows one highlighted vertical slice.

When the vertical slices are rotated about the \(y\)-axis we get thin cylinders (see animation) that have radius \(r=x\) and height \(h=x^2\). The area of the cylinder is: \[\begin{aligned} A &=2\pi rh=2\pi(x)(x^2)\\ &=2\pi x^3 \end{aligned}\]
To find the volume we integrate the area of the cylinders from \(x=0\) to \(x=3\): \[\begin{aligned} V &=\int_0^3 A(x)\,dx =2\pi\int_0^3 x^3\,dx\\ &=2\pi\left[ \dfrac{x^4}{4}\right]_0^3 =2\pi\left(\dfrac{3^4}{4}-0\right)\\ &=\dfrac{81\pi}{2} \end{aligned}\]
ar
-
\(x=y^2\), \(\,y=0\) and \(x=16\) about \(x\)-axis
Use a \(y\)-integral and cylinders. Here is a plot of the region and one highlighted rectangle:

\(V=128\pi\)
Since \(x\) is a function of \(y\), we shall use a \(y\)-integral, with horizontal slices. The diagram shows one highlighted horizontal slice.

When the horizontal slices are rotated about the \(x\)-axis we get thin cylinders (see animation) with radii \(r=y\) and height \(h=x_\text{big}-x_\text{small}=16-y^2\). So the area of the cylinder is: \[\begin{aligned} A&=2\pi rh=2\pi(y)(16-y^2) \\ &=2\pi(16y-y^3) \end{aligned}\]
To find the volume we integrate the area from \(y=0\) to \(y=4\): \[\begin{aligned} V &=\int_0^4 A(y)\,dy =2\pi\int_0^4 (16y-y^3)\,dy\\ &=2\pi\left[8y^2-\dfrac{y^4}{4}\right]_0^4 =2\pi\left(8\cdot4^2-\dfrac{4^4}{4}\right)\\ &=128\pi \end{aligned}\]
ar
-
\(y=e^{-x^2}\), \(y=0\), \(x=0\), and \(x=1\) about \(y\)-axis
When integrating, try a substitution.
\(V=\pi\left(1-\dfrac{1}{e}\right)\)
Since \(y\) is a function of \(x\), we shall use an \(x\)-integral, with vertical slices. The diagram shows the region and one highlighted vertical slice.
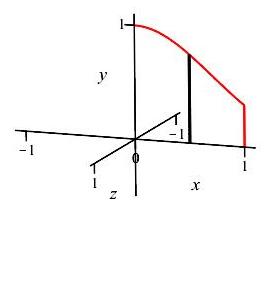
When these vertical slices are rotated about the \(y\)-axis they produce thin cylinders (see animation) with radii \(r=x\) and height \(h=y=e^{-x^2}\). So the area of the cylinder is: \[ A=2\pi rh=2\pi xe^{-x^2} \]
The limits of integration are given as \(x=0\) to \(x=1\). Therefore, the volume is: \[ V=\int_0^1 A(x)\,dx =2\pi\int_0^1 xe^{-x^2}\,dx \] To complete the integral, we use the substitution, \(u=-x^2\). Then \(du=-2xdx\) and so \(xdx=-\,\dfrac{1}{2}\,du\). The limits change to \(u=0\) to \(u=-1\). Therefore:
\[\begin{aligned} V&=-\dfrac{2\pi}{2}\int_0^{-1} e^{u}\,du =-\pi\left[e^u\rule{0pt}{10pt}\right]_0^{-1} \\ &=-\pi(e^{-1}-1) =\pi\left(1-\dfrac{1}{e}\right) \end{aligned}\]
Although the volume looks like it's negative, it is not. Since \(e^{-1} < 1\), \(\,(e^{-1}-1)\) is negative, therefore, \(-\pi(e^{-1}-1)\) is positive.
ar
-
\(y=x^2+2\),\(\quad y=0\),\(\quad x=0\) and \(x=3\) about \(x=4\)
\(V=\dfrac{123}{2}\pi\)
Here \(y\) is a function of \(x\), so we use an \(x\)-integral. with vertical slices. The diagram shows the region, one highlighted vertical slice and the axis of rotation.

When these vertical slices are rotated about the line \(x=4\), we get thin cylinders (see animation) with radius \(r=4-x\) and height \(h=y=x^2+2\). The area of the cylindical surface is: \[\begin{aligned} A&=2\pi rh=2\pi(4-x)(x^2+2) \\ &=2\pi(4x^2+8-x^3-2x) \end{aligned}\]
The limits of integration are given as \(x=0\) and \(x=3\). To find the volume, we integrate the surface area between these limits: \[\begin{aligned} V &=\int_0^3 A(x)\,dx\\ &=\int_0^3 2\pi(4x^2+8-x^3-2x)\,dx\\ &=2\pi\left[4\dfrac{x^3}{3}+8x-\dfrac{x^4}{4}-x^2\right]_0^3\\ &=2\pi\left(4\dfrac{3^3}{3}+8(3)-\dfrac{3^4}{4}-3^2\right)\\ &=2\pi\dfrac{123}{4}=\dfrac{123}{2}\pi \end{aligned}\]
ar
-
\(y=2\sqrt{ax}\) (for \(a>0\)), \( y=0\) and \(x=a\) about the: (use \(x\)-integrals)
-
\(y\)-axis
Use an \(x\)-integral and cylinders. Here is a plot of the region and one highlighted rectangle:

\(V=\dfrac{8}{5}\pi a^3\)
Since \(y\) is a function of \(x\), we use an \(x\)-integral, with vertical slices. The diagram shows the region and one highlighted vertical slice.

When these vertical slices are rotated about the \(y\)-axis we get thin cylinders (see animation) with radius \(r=x\) and height \(h=y=2\sqrt{ax}\). So the surface area of a cylinder is: \[\begin{aligned} A &=2\pi rh=2\pi(x)(2\sqrt{ax})\\ &=4\pi\sqrt{a}\, x^{3/2} \end{aligned}\]
To find the volume, we integrate the area of cylinders from \(x=0\) to \(x=a\). Therefore, the volume is: \[\begin{aligned} V &=\int_0^a A(x)\,dx =4\pi\sqrt{a} \int_0^a x^{3/2}\,dx \\ &=4\pi\sqrt{a}\left[\dfrac{2}{5}x^{5/2}\right]_0^a =\dfrac{8}{5}\pi\sqrt{a}a^{5/2} \\ &=\dfrac{8}{5}\pi a^3 \end{aligned}\]
This is the exact same volume as in part (a) of a previous exercise just calculated using thin cylinders instead of washers!
ar
-
\(x=a\)
Again, use an \(x\)-integral and cylinders. Here is a plot of the region and one highlighted vertical slice.

\(V=\dfrac{16}{15}\pi a^3\)
Again, \(y\) is a function of \(x\), so we use an \(x\)-integral, with vertical slices. The diagram shows the region and one highlighted vertical slice.

When these vertical slices are rotated about the line \(x=a\), we get thin cylinders (see animation) with radius \(r=a-x\) and height \(h=y=2\sqrt{ax}\) So the area of the thin cylinders is: \[\begin{aligned} A &=2\pi rh=2\pi(a-x)(2\sqrt{ax}) \\ &=4\pi\sqrt{a}(a\sqrt{x}-x^{3/2}) \end{aligned}\]
To find the volume, we integrate the area from \(x=0\) to \(x=a\). Therefore the volume is: \[\begin{aligned} V &=\int_0^a A(x)\,dx\\ &=4\pi\sqrt{a} \int_0^a (a\sqrt{x}-x^{3/2})\,dx \\ &=4\pi\sqrt{a} \left[ a\dfrac{2}{3}x^{3/2}-\dfrac{2}{5}x^{5/2}\right]_0^a\\ &=4\pi\sqrt{a} \left(a\dfrac{2}{3}a^{3/2}-\dfrac{2}{5}a^{5/2}\right) \\ &=8\pi\sqrt{a}\,a^{5/2} \left(\dfrac{1}{3}-\dfrac{1}{5}\right) =\dfrac{16}{15}\pi a^3 \end{aligned}\]
This is the exact same volume as in part (b) of a previous exercise just calculated using thin cylinders instead of disks!
ar
-
\(x=2a\)
Once again, use an \(x\)-integral and cylinders. The diagram shows the region, one highlighted vertical slice and the axis of rotation.

\(V=\dfrac{56}{15}\pi a^3\)
Once again, \(y\) is a function of \(x\), so we use an \(x\)-integral, with vertical slices. The diagram shows the region, one highlighted vertical slice and the axis of rotation.

When these vertical slices are rotated about the line \(x=2a\), we get thin cylinders (see animation) with radius \(r=2a-x\) and height \(h=y=2\sqrt{ax}\). So the area of the thin cylinders is: \[\begin{aligned} A &=2\pi rh=2\pi(2a-x)(2\sqrt{ax})\\ &=4\pi\sqrt{a}(2a\sqrt{x}-x^{3/2}) \end{aligned}\]
To find the volume, we integrate the area from \(x=0\) to \(x=a\): \[\begin{aligned} V &=\int_0^a A(x)\,dx \\ &=4\pi\sqrt{a}\int_0^a (2a\sqrt{x}-x^{3/2})\,dx \\ &=4\pi\sqrt{a}\left[\dfrac{4}{3}ax^{3/2} -\dfrac{2}{5}x^{5/2}\right]_0^a\\ &=4\pi\sqrt{a}\left(\dfrac{4}{3}a^{5/2}-\dfrac{2}{5}a^{5/2}\right)\\ &=\dfrac{56}{15}\pi a^3 \end{aligned}\]
This is the exact same volume as in part (c) of a previous exercise just calculated using thin cylinders instead of washers!
ar
-
-
\(y=(x-2)^2\) and \(y=4-x\) about
-
\(x\)-axis
\(V=\dfrac{72}{5}\pi\)
Since \(y\) is a function of \(x\), we shall use an \(x\)-integral with vertical slices. (Also if we had used a \(y\)-integral we would have had to split the integral into two parts.) The diagram on the right shows the region of integration along with one highlighted vertical slice.
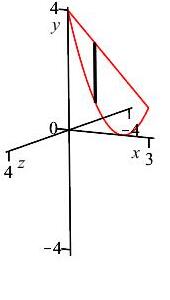
From the figure, we know that in \(4-x \ge (x-2^2)\). Rotating the vertical slices about the \(x\)-axis gives us washers (see animation) with outer radii \(R=4-x\) and inner radii \(r=(x-2)^2\). Therefore, the area of the cross-section is: \[\begin{aligned} A &=\pi(R^2-r^2)\\ &=\pi[(4-x)^2-(x-2)^4] \end{aligned}\]
To get the limits we must equate the given functions and solve for \(x\): \[\begin{aligned} (x-2)^2 &=4-x\\ x^2-4x+4 &=4-x\\ x^2-3x &=0\\ x(x-3) &=0 \end{aligned}\] Therefore the limits are from \(x=0\) to \(x=3\). So the volume is:
\[\begin{aligned} V &=\int_0^3 A(x)\,dx\\ &=\pi\int_0^3 ((4-x)^2-(x-2)^4)\,dx\\ &=\pi\left[-\dfrac{(4-x)^3}{3}-\dfrac{(x-2)^5}{5}\right]_0^3\\ &=\pi\left[\left(-\dfrac{1}{3}-\dfrac{1}{5}\right) -\left(-\dfrac{4^3}{3}-\dfrac{(-2)^5}{5}\right)\right]\\ &=\dfrac{72}{5}\pi \end{aligned}\]
ar
-
\(y\)-axis
\(V=\dfrac{27}{2}\pi\)
Similar to part (a), we use an \(x\)-integral and the limits of integration are from \(x=0\) to \(x=3\). The diagram on the right shows the region of integration along with one highlighted vertical slice.
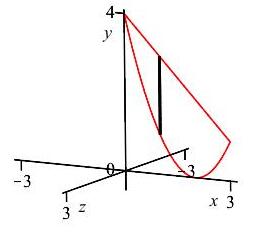
However, here when the vertical slices are rotated about the \(y\)-axis, we get thin cylinders with radii \(r=x\) and height \(h=(4-x)-(x-2)^2\). The surface area of the thin cylinders is: \[\begin{aligned} A &=2\pi rh=2\pi x[(4-x)-(x-2)^2]\\ &=2\pi x [4-x-(x^2-4x+4)]\\ &=2\pi x [ 3x-x^2]\\ &=2\pi(3x^2-x^3) \end{aligned}\]
So the volume is: \[\begin{aligned} V &=2\pi\int_0^3 (3x^2-x^3)\,dx \\ &=2\pi\left[x^3-\dfrac{x^4}{4}\right]_0^3\\ &=2\pi\left(3^3-\dfrac{3^4}{4}\right) =\dfrac{27}{2}\pi \end{aligned}\]
ar
-
-
\(x=4-(y-2)^2\) and \(x=0\) about
-
\(x\)-axis
\(V=\dfrac{128}{3}\pi\)
We use a \(y\)-integral since we are given a function of \(y\). The diagram on the right shows a plot of the described region with one highlighted horizontal slice.
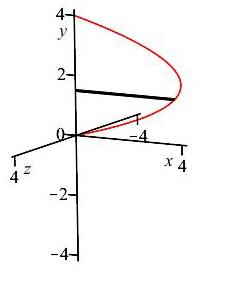
Rotating the horizontal slices about the \(x\)-axis gives us thin cylinders (see animation) with radius \(r=y\) and height \(h=x=4-(y-2)^2\). Therefore, the surface area of the cylinders is: \[\begin{aligned} A &=2\pi rh=2\pi y(4-(y-2)^2)\\ &=2\pi y(-y^2+4y))\\ &=2\pi(-y^3+4y^2) \end{aligned}\]
To get the limits we solve the equation: \[\begin{aligned} 4-(y-2)^2&=0\\ -y^2+4y&=0\\ -y(y-4)&=0 \end{aligned}\] Therefore the limits are from \(y=0\) to \(y=4\). So the volume is:
\[\begin{aligned} V &=\int_0^4 A(y)\,dy\\ &=2\pi\int_0^4 (-y^3+4y^2)\,dy\\ &=2\pi\left[-\dfrac{y^4}{4}+4\dfrac{y^3}{3}\right]_0^4\\ &=2\pi\left(-\dfrac{4^4}{4}+4\dfrac{4^3}{3}\right)\\ &=2\pi4^3 \left[-1+\dfrac{4}{3}\right] =\dfrac{128}{3}\pi \end{aligned}\]
ar
-
\(y\)-axis
\(V=\dfrac{512}{15}\pi\)
Similar to part (a), we use a \(y\)-integral and the limits of integration are from \(y=0\) to \(y=4\). The diagram on the right shows the region of integration along with one highlighted horizontal slice.
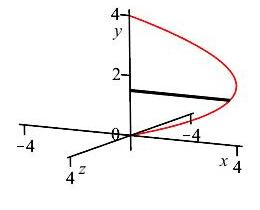
However, when the horizontal slices are rotated about the \(y\)-axis, we get disks with radii \(R=x=4-(y-2)^2\). Therefore, the area of the cross-section is: \[\begin{aligned} A &=\pi R^2=\pi(4-(y-2)^2)^2\\ &=\pi(-y^2+4y)^2\\ &=\pi(y^4-8y^3+16y^2) \end{aligned}\]
So the volume is: \[\begin{aligned} V &=\int_0^4 A(y)\,dy \\ &=\pi\int_0^4 (y^4-8y^3+16y^2)\,dy \\ &=\pi\left[\dfrac{y^5}{5}-2y^4+\dfrac{16y^3}{3}\right]_0^4 \\ &=\pi\left(\dfrac{4^5}{5}-2\cdot4^4+\dfrac{16\cdot4^3}{3}\right) \\ &=\pi4^4\left(\dfrac{4}{5}-2+\dfrac{4}{3}\right) =\dfrac{512}{15}\pi \end{aligned}\]
ar
-
-
\(y=\ln x\), \(y=0\) and \(x=e\) about
-
\(x\)-axis
\(x\)-integral using disks. You will need to integrate by parts.
\(V=\pi e-2\pi\)
We use an \(x\)-integral since we are given \(y\) as a function of \(x\). The diagram shows a plot of the described region with one highlighted vertical slice.
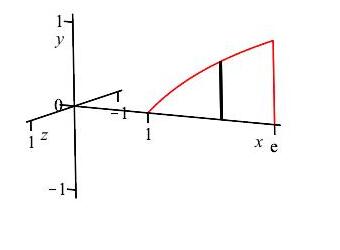
Rotating the vertical slices about the \(x\)-axis gives disks, with radii \(R=y=\ln x\). The area of the disk is: \[ A=\pi R^2=\pi(\ln x)^2 \] The limits of integration are from \(x=1\) (where \(y=0\)) to \(x=e\).
Therefore, the volume is: \[\begin{aligned} V &=\int_1^e \pi(\ln x)^2\, dx \end{aligned}\] We apply integration by parts with: \[\begin{array}{ll} u=(\ln x)^2 & dv=\pi\,dx \\ du=\dfrac{2\ln x}{x}\,dx \quad & v=\pi x \end{array}\] So the indefinite integral is:
\[\begin{aligned} \int \pi(\ln x)^2\, dx&=\pi x(\ln x)^2-\int (\pi x) \dfrac{2\ln x}{x}\,dx\\ &=\pi x(\ln x)^2-2\pi\int \ln x\,dx\\ &=\pi x(\ln x)^2-2\pi(x\ln x-x)+C \end{aligned}\] Finally, the volume is: \[\begin{aligned} V &=\left[\pi x(\ln x)^2-2\pi x\ln x+2\pi x\rule{0pt}{10pt}\right]_1^e\\ &=\pi e-2\pi \end{aligned}\]
ar,lk
-
\(y\)-axis
\(x\)-integral using cylinders. You will need to integrate by parts.
\(V=\dfrac{\pi}{2}(e^2+1)\)
As in part (a), we use an \(x\)-integral and the limits are from \(x=1\) to \(x=e\). The diagram shows the region of integration along with one highlighted vertical slice.
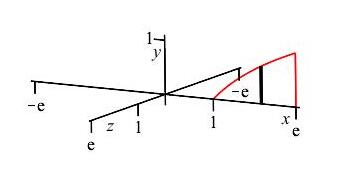
However, when the vertical slices are rotated about the \(y\)-axis, we get thin cylinders with radii \(r=x\) and height \(h=y=\ln x\). Therefore, the surface area of the cylinders is: \[ A=2\pi rh=2\pi x \ln x \]
Therefore, the volume is: \[\begin{aligned} V &=\int_1^e 2\pi x\ln x\,dx \end{aligned}\] We apply integration by parts with: \[\begin{array}{ll} u=\ln x & dv=2\pi x\,dx \\ du=\dfrac{1}{x}\,dx \quad & v=\pi x^2 \end{array}\] So the indefinite integral is:
\[\begin{aligned} \int 2\pi x\ln x\,dx&=\pi x^2\ln x-\int (\pi x^2)\dfrac{1}{x}\,dx\\ &=\pi x^2\ln x-\pi \int x\,dx\\ &=\pi x^2\ln x-\pi\dfrac{x^2}{2}+C \end{aligned}\] Finally, the volume is: \[\begin{aligned} V &=\left[\pi x^2\ln x-\pi\dfrac{x^2}{2}\right]_1^e\\ &=\left(\pi\dfrac{e^2}{2}\right)-\left(-\pi\dfrac{1}{2}\right) =\dfrac{\pi}{2}(e^2+1) \end{aligned}\]
ar,lk
-
-
\(y=e^{-x}\), \(y=0\), \(x=0\) and \(x=k\) (with \(k>0\)) about
-
\(x\)-axis. Then find the limit as \(k\to\infty\).
\(x\)-integral using disks.
\(V=\dfrac{\pi}{2}(1-e^{-2k})\)
\(\displaystyle \lim_{k\to\infty}V=\dfrac{\pi}{2}\)We use an \(x\)-integral. So the slices are vertical and the limits are from \(x=0\) to \(x=k\).
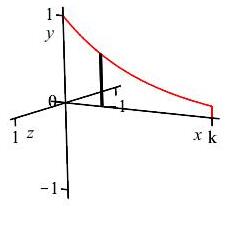
When the vertical slices are rotated about the \(x\)-axis, we get disks (see animation) with radii \(r=y=e^{-x}\). So the area of a disk is: \[ A=\pi r^2=\pi e^{-2x} \] And the volume is:
\[\begin{aligned} V &=\int_0^k A(x)\,dx =\pi\int_0^k e^{-2x}\,dx\\ &=\pi\left[\dfrac{-e^{-2x}}{2}\right]_0^k\\ &=\pi\left[\dfrac{-e^{-2k}}{2}-\left(\dfrac{-1}{2}\right)\right]\\ &=\dfrac{\pi}{2}(1-e^{-2k}) \end{aligned}\] So \[ \lim_{k\to\infty}V=\lim_{k\to\infty}\dfrac{\pi}{2}(1-e^{-2k}) =\dfrac{\pi}{2} \]
ar,lk
-
\(y\)-axis. Then find the limit as \(k\to\infty\).
\(x\)-integral using cylinders. You will need to integrate by parts.
\(V=2\pi(1-ke^{-k}-e^{-k})\)
\(\displaystyle \lim_{k\to\infty}V=2\pi\)Again we use an \(x\)-integral with vertical slices and the limits are from \(x=0\) to \(x=k\).
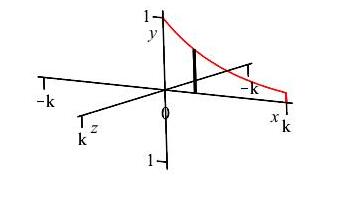
This time, the slices are rotated about the \(y\)-axis to give cylinders with radii \(r=x\) and height \(h=y=e^{-x}\). So the area of a cylinder is: \[ A=2\pi rh=2\pi xe^{-x} \] Therefore, the volume is:
\[\begin{aligned} V &=\int_0^k A(x)\,dx=\int_0^k 2\pi xe^{-x}\,dx \end{aligned}\] We now intgrate by parts with \[\begin{array}{ll} u=2\pi x & dv=e^{-x}\,dx \\ du=2\pi\,dx \quad & v=-e^{-x} \end{array}\]
So the indefinite integral is: \[\begin{aligned} \int 2\pi xe^{-x}\,dx &=-2\pi x e^{-x}+2\pi\int e^{-x}\,dx\\ &=-2\pi x e^{-x}-2\pi e^{-x}+C\\ \end{aligned}\] And, the volume is: \[\begin{aligned} V &=\left[-2\pi x e^{-x}-2\pi e^{-x}\rule{0pt}{10pt}\right]_0^k \\ &=(-2\pi k e^{-k}-2\pi e^{-k})-(-2\pi) \\ &=2\pi(1-ke^{-k}-e^{-k}) \end{aligned}\] So \[ \lim_{k\to\infty}V=\lim_{k\to\infty}2\pi(1-ke^{-k}-e^{-k}) =2\pi \]
ar,lk
-
-
For the ellipse \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) \((0 < b < a)\)
-
Compute the area enclosed by its graph.
Express \(y\) in terms of \(x\).
\(A=\pi ab \)
We first express \(y\) in terms of \(x\): \[\begin{aligned} &\dfrac{y^2}{b^2}=1-\dfrac{x^2}{a^2}\\ &y_\pm=\pm b\sqrt{1-\dfrac{x^2}{a^2}} \end{aligned}\] The limits of integration are the \(x\)-intercepts \(x=-a\) and \(x=a\). Therefore, the area of the ellipse is:
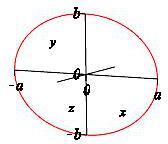
\[\begin{aligned} A&=\int_{-a}^a y_+-y_-\,dx\\ &=2\int_{-a}^a b\sqrt{1-\dfrac{x^2}{a^2}}\,dx \end{aligned}\] We now use the trigonometric substitution \(x=a\sin\theta\) and \(dx=a\cos\theta\,d\theta\). The limits change to \(\theta=-\,\dfrac{\pi}{2}\) to \(\theta=\dfrac{\pi}{2}\). Therefore the volume is: \[\begin{aligned} A&=2b \int_{-\pi/2}^{\pi/2} \sqrt{1-\dfrac{a^2\sin^2\theta}{a^2}}a\cos\theta\,d\theta \\ &=2ab \int_{-\pi/2}^{\pi/2} \cos^2\theta\,d\theta =2ab \int_{-\pi/2}^{\pi/2} \dfrac{1+\cos{2\theta}}{2}\,d\theta \\ &=ab \left[\theta+\dfrac{\sin{2\theta}}{2}\right]_{-\pi/2}^{\pi/2} =\pi ab \end{aligned}\]
ar
Notice this is a version is integration by slicing. We integrate the the length of the perpendicular slice to get the total area.
-
Compute the volume of the ellipsoid generated by revolving the ellipse about the \(x\)-axis.
\(x\)-integral using disks.
\(V=\dfrac{4}{3}\) \(\pi ab^2\)
The volume is obtained by rotating the upper half of the ellipse about the \(x\)-axis. The plot shows the ellipse and one highlighted vertical slice on the upper half.
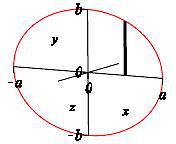
We rotate the vertical slices about the \(x\)-axis producing disks (see animation) with radii \(r=y_+=b\sqrt{1-\dfrac{x^2}{a^2}}\). So the area of the disk is: \[ A=\pi r^2=\pi b^2\left(1-\dfrac{x^2}{a^2}\right) \]
To find the volume, we integrate the area from \(x=-a\) to \(x=a\). \[\begin{aligned} V &=\pi b^2 \int_{-a}^a \left(1-\dfrac{x^2}{a^2}\right)\,dx\\ &=\pi b^2 \left[x-\dfrac{x^3}{3a^2}\right]_{-a}^a\\ &=2\pi b^2 \left(a-\dfrac{a^3}{3a^2}\right)\\ &=2\pi b^2 \left(\dfrac{2a}{3}\right) =\dfrac{4}{3}\pi ab^2 \end{aligned}\]
-
-
The region bounded by the circle \(x^2+y^2=b^2\) is revolved about the \(x=a\) (with \(0 \lt b \lt a\)). Find the volume of the resulting donut-shaped solid (called a torus).
-
Use an \(x\)-integral.
\(V=2\pi^2ab^2\)
Since we are using an \(x\)-integral the slices are vertical. The plot shows the circle, one highlighted vertical slice and the axis of rotation.
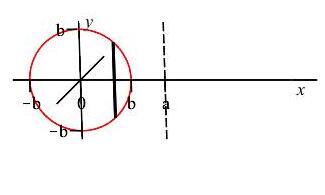
Rotating a vertical slice about the line \(x=a\), gives a cylindrical shell (see animation) whose radius is \(r=a-x\). We solve the equation of the circle for the upper and lower values of \(y\): \[ y_\pm=\pm\sqrt{b^2-x^2} \] Therefore, the height of the cylinder is \(h=y_+-y_-=2\sqrt{b^2-x^2}\). So the surface area of the cylindrical shell is:
\[\begin{aligned} A &=2\pi rh=2\pi(a-x)(2\sqrt{b^2-x^2})\\ &=4\pi(a-x)\sqrt{b^2-x^2} \end{aligned}\] To obtain the volume we integrate the area from \(x=-b\) to \(x=-b\):
\[\begin{aligned} V &=\int_{-b}^b 4\pi(a-x)\sqrt{b^2-x^2}\,dx\\ &=4\pi a\int_{-b}^b \sqrt{b^2-x^2}\,dx-4\pi\int_{-b}^b x\sqrt{b^2-x^2}\,dx\\ \end{aligned}\] Here, the second term in an odd function on a symmetric interval, \([-b,b]\), and so gives \(0\). The first term can be done using the trigonometric substitution, \(x=b\sin\theta\). However, it is easier to recognize that the integral is the area under the graph of \(f(x)=\sqrt{b^2-x^2}\) from \(x=-b\) to \(x=b\) which is a semicircle of radius \(b\) and so area \[ \int_{-b}^b \sqrt{b^2-x^2}\,dx=\dfrac{1}{2}\pi b^2 \] Therefore, the volume is: \[ V=4\pi a \dfrac{1}{2}\pi b^2 -0=2\pi^2 ab^2 \]
lk
-
Use a \(y\)-integral.
\(V=2\pi^2a^2b\)
Since we are using an \(y\)-integral the slices are horizontal. The plot shows the circle, one highlighted horizontal slice and the axis of rotation.
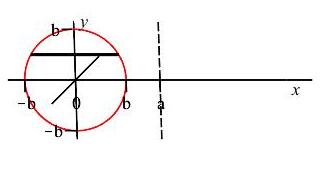
Rotating a horizontal slice about the line \(x=b\), gives a washer (see animation) whose inner radius is \(r=b-x=b-\sqrt{a^2-y^2}\) and outer radius is \(R=b+x=b+\sqrt{a^2-y^2}\). So the area of the washer is:
\[\begin{aligned} A&=\pi(R^2-r^2)=\pi(R+r)(R-r) \\ &=4\pi b\sqrt{a^2-y^2} \end{aligned}\] To obtain the volume we integrate the area from \(y=-a\) to \(y=-a\):
\[\begin{aligned} V &=\int_{-a}^a 4\pi b\sqrt{a^2-y^2}\,dy\\ &=4\pi b\int_{-a}^a\sqrt{a^2-y^2}\,dy \end{aligned}\] This can be done using the trigonometric substitution, \(y=a\sin\theta\). However, it is easier to recognize that the integral is the area under the graph of \(f(y)=\sqrt{a^2-y^2}\) from \(y=-a\) to \(y=-a\) which is a semicircle of radius \(a\) and so area \[ \int_{-a}^a \sqrt{a^2-y^2}\,dy=\dfrac{1}{2}\pi a^2 \] Therefore, the volume is: \[ V=4\pi b \dfrac{1}{2}\pi a^2=2\pi^2 a^2 b \]
lk
-
-
The base of a solid is the region bounded by \(y=e^x\), \(x=0\) and \(y=e\). The cross-sections perpendicular to the \(x\)-axis are rectangles whose height is equal to half of its base. Find the volume.
\(V=\dfrac{4e-e^2-1}{4}\)
The line segment on the base perpendicular to the \(x\)-axis has endpoints \(x_\text{top}=e\) and \(x_\text{bottom}=e^{x}\). So the base of the rectangular cross-section has length \(b=x_\text{top}-x_\text{bottom}=e-e^{x}\). The height of the cross-section is equal to the half the base: \(h=\dfrac{b}{2}=\dfrac {e-e^{x}}{2}\). So the cross-sectional area is: \[ A=bh=\dfrac{1}{2}(e-e^{x})^2 =\dfrac{1}{2}(e^2-2e^{x+1}+e^{2x}) \]
To find the volume, we integrate the area along the \(x\)-axis from \(x=0\) to \(x=1\): \[\begin{aligned} V&=\int_0^1 A(x) \,dx =\dfrac{1}{2} \int_0^1 (e^2-2e^{x+1}+e^{2x})\,dx\\ &=\dfrac{1}{2} \left[e^2 x-2e^{x+1}+\dfrac{1}{2}e^{2x} \right]_0^1\\ &=\dfrac{1}{2} \left(e^2-2e^2+\dfrac{1}{2}e^2\right)-\dfrac{1}{2} \left(-2e+\dfrac{1}{2}\right)\\ &=-\dfrac{1}{4}e^2+e-\dfrac{1}{4}\\ &=\dfrac{4e-e^2-1}{4} \end{aligned}\]
ar
-
A pyramid has a square base with side \(s\) and height \(h\). Prove its volume is \(V=\dfrac{1}{3}hs^2\).
A helpful way to orient the pyramid is to place the vertex at the origin and the altitude of the pyramid along the positive \(x\)-axis. In this position, the pyramid is the solid with square cross-sections perpendicular to the \(x\)-axis.
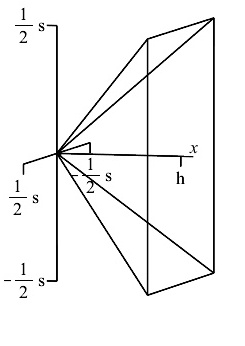
A helpful way to orient the pyramid is to place the vertex at the origin and the altitude of the pyramid along the positive \(x\)-axis. In this position, the pyramid is the solid with square cross-sections perpendicular to the \(x\)-axis. Since, the volume is an \(x\)-integral, we need to express the area of a each square cross-section in terms of \(x\).
Suppose \(a\) is the side of a general square cross-section \(x\) units from the the origin, then by similar triangles we get: \[ \dfrac{a}{x}=\dfrac{s}{h} \quad \implies \quad a=\dfrac{s}{h}x \] where \(s\) and \(h\) are the base length and height of the pyramid respectively. Therefore the cross-sectional area is: \[ A(x)=a^2=\dfrac{s^2}{h^2}x^2 \] To obtain the volume of the pyramid, we integrate the area of the cross-section from \(x=0\) to \(x=h\): \[\begin{aligned} V&=\int_0^h A(x)\,dx =\int_0^h \dfrac{s^2}{h^2}x^2\,dx\\ &=\dfrac{s^2}{h^2} \left[\dfrac{x^3}{3}\right]_0^h =\dfrac{s^2}{h^2}\dfrac{h^3}{3}=\dfrac{1}{3}hs^2 \end{aligned}\] Hence we have proved that the volume of a pyramid with a square base with side \(s\) and height \(h\) is \(V=\dfrac{1}{3}hs^2\).
More generally, the volume of any pyramid is \(V=\dfrac{1}{3}hA\) where \(A\) is the area of the base.
-
\(y=x-x^2\), \(y=0\) about \(y\)-axis
\(V=\dfrac{1}{6}\pi\)
We use an \(x\)-integral. The vertical slices rotate about the \(y\)-axis to give cylinders. The radius of a cylinder is \(r=x\) and the height is \(h=x-x^2\). The limits of integration are from \(x=0\) to \(x=1\). Therefore, the volume is: \[\begin{aligned} V&=\int_0^1 2\pi rh\,dx =\int_0^1 2\pi x(x-x^2)\,dx \\ &=2\pi\left[\dfrac{x^3}{3}-\dfrac{x^4}{4}\right]_0^1 =2\pi\left(\dfrac{1}{3}-\dfrac{1}{4}\right) =\dfrac{1}{6}\pi \end{aligned}\]
-
\(x=\sqrt{y}\), \(x=0\), \(y=4\) about \(x=3\)
\(\displaystyle V=24\pi\)
We first use a \(y\)-integral. The slices are horizontal which rotate about \(x=3\) to give washers. The outer radius of the washers is \(R=3\) and the inner radius is \(r=3-\sqrt{y}\). The limits of integration are from \(y=0\) to \(y=4\). Therefore, the volume is:
\[\begin{aligned} V&=\int_0^4 \pi R^2-\pi r^2 \,dy \\ &=\pi\int_0^4 [(3)^2-(3-\sqrt{y})^2]\,dy \\ &=\pi\int_0^4 (6\sqrt{y}-y)\,dy \\ &=\pi\left[4y^{3/2}-\dfrac{y^2}{2}\right]_0^4 \\ &=\pi\left(4\cdot4^{3/2}-\dfrac{4^2}{2}\right) =24\pi \end{aligned}\]
We now use an \(x\)-integral. So we rewrite the curved edge as \(y=x^2\). The slices are vertical which rotate about \(x=3\) to give cylinders. The radius of the cylinders is \(r=3-x\) and the height is \(h=4-x^2\). The limits of integration are now \(x=0\) to \(x=2\). Therefore, the volume is: \[\begin{aligned} V&=2\pi\int_0^2 rh\,dx =2\pi\int_0^2 (3-x)(4-x^2)\,dx \\ &=2\pi\int_0^2 (12-4x-3x^2+x^3)\,dx \\ &=2\pi\left[12x-2x^2-x^3+\dfrac{x^4}{4}\right]_0^2 \\ &=2\pi(24-8-8+4) =24\pi \end{aligned}\]
-
\(y=\sin x\), \(y=0\), from \(x=0\) to \(x=\pi\) about \(y\)-axis
\(V=2\pi^2\)
This is an \(x\)-integral. The vertical slices rotate about the \(y\)-axis to give cylinders. The radius of a cylinder is \(r=x\) and the height is \(h=\sin x\). The limits of integration are from \(x=0\) to \(x=\pi\). Therefore, the volume is: \[ V=\int_0^\pi 2\pi rh\,dx =2\pi\int_0^\pi x\sin x\,dx \] To do the integration, we integrate by parts with \(\begin{array}{ll} u=x & dv=\sin x\,dx \\ du=dx \quad & v=-\cos x \end{array}\).
Then: \[\begin{aligned} V&=2\pi\left[-x\cos x+\int\cos x\,dx\right]_0^\pi \\ &=2\pi\left[-x\cos x+\sin x\rule{0pt}{10pt}\right]_0^\pi \\ &=2\pi(-\pi\cos\pi) =2\pi^2 \end{aligned}\]
-
\(y=\sqrt{x}\), \(y=0\), \(x=4\)
-
About \(x\)-axis
\(V=8\pi\)
We use an \(x\)-integral. The vertical slices rotate about the \(x\)-axis to give disks. The radius of a disk is \(r=\sqrt{x}\). The limits of integration are from \(x=0\) to \(x=4\). Therefore, the volume is: \[\begin{aligned} V&=\int_0^4 \pi r^2 \,dx =\int_0^4 \pi(\sqrt{x})^2 \,d \\ &=\pi\int_0^4 x\,dx =\pi\left[\dfrac{x^2}{2}\right]_0^4 =8\pi \end{aligned}\]
-
In the previous exercise, we computed the volume of the solid swept out by rotating the region bounded by \(y=\sqrt{x}\), \(y=0\) and \(x=4\) about \(x\)-axis. At what value of \(x=c\) in \((0,4)\) would a plane perpendicular to the \(x\)-axis need to be placed to divide the solid into two parts of equal volume?
\(c=2\sqrt{2}\)
From the previous problem, we know the full volume is: \[ V=\int_0^4 \pi(\sqrt{x})^2\,dx=8\pi \] Half this volume is \(4\pi\). So we want to find \(c\) in \((0,4)\), so that: \[ 4\pi=V_c=\int_0^c \pi(\sqrt{x})^2\,dx =\pi\left[\dfrac{x^2}{2}\right]_0^c =\dfrac{c^2}{2}\pi \] So we solve \(\dfrac{c^2}{2}\pi=4\pi\) and find \(c=2\sqrt{2}\).
PY: All Checked.
In each problem:
i. Draw the base.
ii. Draw a line on the base perpendicular to the indicated axis. Find its length.
iii. Draw the cross-section of the solid above this line. Find its area.
iv. Integrate the cross-sectional areas to find the volume.
In each problem, the planar region bounded by the given equations is rotated about the indicated line to sweep out a volume. Will you do an \(x\)-integral or a \(y\)-integral? Are the Riemann sum rectangles horizontal or vertical? When the rectangle is rotated, does it sweep out a thin disk, thin washer or thin cylinder?
Use thin disks to compute the volume of the solid generated by revolving the plane region bounded by the given equations about the indicated line.
Use thin washers to compute the volume of the solid generated by revolving the plane region bounded by the given equations about the indicated line.
Use thin cylinders to compute the volume of the solid generated by revolving the plane region bounded by the given equations about the indicated line.
Use any appropriate method to compute the volume of the solid generated by revolving the plane region bounded by the given equations about the indicated line. These are the most important problems since they don't tell you which method to use.
Review Exercises
Find the volume of the solid formed by revolving the given region about the given line.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum