13. Volume

b1. Solids of Revolution

If a region in the \(xy\)-plane is rotated about some axis, it sweeps out a solid called a Solid of Revolution. For example, here are four regions in the \(xy\)-plane and the solids swept out when they are rotated about the \(x\)-axis or the \(y\)-axis:

  1. Area below \(y=f(x)\) above \(x\)-axis rotated about \(x\)-axis and \(y\)-axis:
    Region 1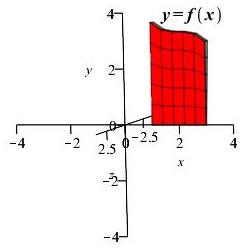
    The plot shows the region below the function y = f of x above the x axis.
    Region 1 \(x\)-axis
    Region 1 \(y\)-axis
  2. Area below \(y=f(x)\) above \(y=g(x)\) rotated about \(x\)-axis and \(y\)-axis:
    Region 2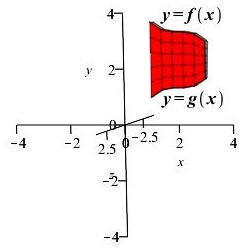
    The plot shows the region below y = f of x above y = g of x.
    Region 2 \(x\)-axis
    Region 2 \(y\)-axis
  3. Area left of \(x=f(y)\) right of \(y\)-axis rotated about \(x\)-axis and \(y\)-axis:
    Region 3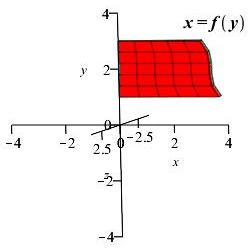
    This graph shows the area between a function x = f of y and the y axis, to the right of an interval on the y axis.
    Region 3 \(x\)-axis
    Region 3 \(y\)-axis
  4. Area left of \(x=f(y)\) right of \(x=g(y)\) rotated about \(x\)-axis and \(y\)-axis:
    Region 4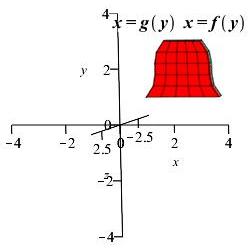
    This graph shows the area between a function x = f of y and another function x = g of y, to the right of an interval on the y axis.
    Region 4 \(x\)-axis
    Region 4 \(y\)-axis
Our goal is to find the volumes of these solids of revolution.

As with all integration problems, we chop the solid up into small pieces, approximate the volume of each piece, add them up and take the limit as the number of pieces gets large and the size of each piece gets small.

For regions 1 and 2, the region is defined in terms of functions of \(x\). So we chop up the \(x\)-interval into small pieces of length \(\Delta x\).

For regions 3 and 4, the region is defined in terms of functions of \(y\). So we chop up the \(y\)-interval into small pieces of length \(\Delta y\).

Here are the corresponding small pieces of the regions and the corresponding small pieces of the volumes of revolution:

  1. Area below \(y=f(x)\) above \(x\)-axis rotated about \(x\)-axis and \(y\)-axis:
    Rectangle 1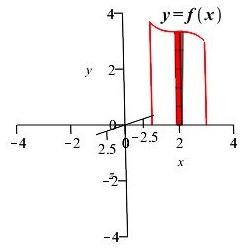
    This shows an thin vertical slice of the region between a function y = f of x and the x axis.
    Rectangle 1 \(x\)-axis

    Rectangle 1 \(y\)-axis

  2. Area below \(y=f(x)\) above \(y=g(x)\) rotated about \(x\)-axis and \(y\)-axis:
    Rectangle 2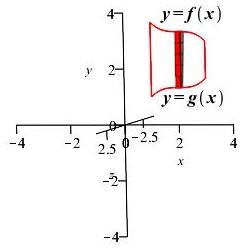
    This shows an thin vertical slice of the region between a function y = f of x and another function y = g of x.
    Rectangle 2 \(x\)-axis

    Rectangle 2 \(y\)-axis

  3. Area left of \(x=f(y)\) right of \(y\)-axis rotated about \(x\)-axis and \(y\)-axis:
    Rectangle 3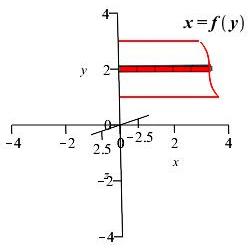
    This shows an thin horizontal slice of the region between a function x = f of y and the y axis.
    Rectangle 3 \(x\)-axis

    Rectangle 3 \(y\)-axis

  4. Area left of \(x=f(y)\) right of \(x=g(y)\) rotated about \(x\)-axis and \(y\)-axis:
    Rectangle 4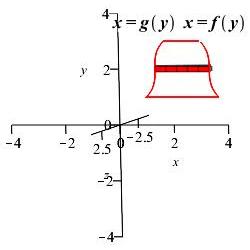
    This shows a thin horizontal slice of the region between a function x = f of y and another function x = g of y.
    Rectangle 4 \(x\)-axis

    Rectangle 4 \(y\)-axis

Notice that:
Rectangles 1x and 3y rotate into thin disks,
Rectangles 2x and 4y rotate into thin washers and
Rectangles 1y, 2y, 3x and 4x rotate into thin cylinders.
(Thin cylinders are also called cylindrical shells.) The integrals are slightly different in each of the three cases.

Do not try to memorize which shape arises from each choice of integration variable and which way it is rotated.

Rather, on subsequent pages, we will explain how to distinguish between them. On the next page we will discuss the general procedure for how to determine the shape. Then on subsequent pages, we will discuss thin disks, thin washers and thin cylinders.

© MY Math Apps

Supported in part by NSF Grant #1123255

NSF logo