13. Volume
a1. Volume by Slicing
Integrals can also be used to find volumes! We start with a method which slices the volume perpendicular to an axis. This time we begin with an example.
Find the volume of the solid whose base is the semicircle \(0 \le y \le \sqrt{9-x^2}\) and whose cross-sections perpendicular to the \(x\)-axis are squares. Here are pictures of the base, the solid and a cross-sectional slice through the solid at position \(x\) so we can see the square cross-section:
_sq_base.jpg)
_sq_solid.jpg)
_sq_sliced.jpg)
Caution: The base here is standing up at the back of the solid, since that is where we usually draw the \(xy\)-plane.
As with all integrals, to compute the volume, we cut the volume up into small pieces, find the volume of each piece, add them up and take the limit as the number of pieces becomes large (\(n\rightarrow\infty\)) and the size of each piece gets small (\(\Delta x\rightarrow0\)). In this case, the pieces are slices perpendicular to the \(x\)-axis, each of thickness \(\Delta x\). So the above picture should be regarded as a loaf of bread which has been sliced. Below is a picture of one slice, the slice at \(x\), and an animation showing the slices being added up to form the solid:
_sq_slice.jpg)
_sq_anim.gif)
The volume of one slice is approximately the area of the square face times the thickness \(\Delta x\). To find the area of the square, we need to know the length of a side. But this is just the height of the semicircle at the position \(x\) of the slice. So the side is \(\displaystyle s=y=\sqrt{9-x^2}\) and the area is: \[ A(x)=s^2=\sqrt{9-x^2}^2=9-x^2 \] Hence the volume of the slice is approximately: \[ \Delta V \approx A(x)\Delta x =(9-x^2)\Delta x \] We now add up these volumes and take the limit as the number of slices becomes large. The result gives the volume as an integral which we evaluate: \[\begin{aligned} V&=\lim_{n\rightarrow\infty}\sum_{i=1}^n\Delta V =\lim_{n\rightarrow\infty}\sum_{i=1}^n(9-x^2)\,\Delta x \\ &=\int_{-3}^3 (9-x^2)\,dx =\left[9x-\dfrac{x^3}{3}\right]_{-3}^3 \\ &=(27-9)-(-27+9)=36 \end{aligned}\]
In other volume by slicing problems, the shape of the base may change and the shape of the cross-sections may change, but in all such problems, we slice the volume perpendicular to some axis, compute the cross-sectional area (This is the hard part.) and integrate over the length of the solid.
If a solid extends from \(x=a\) to \(x=b\) and the cross-sections perpendicular to the \(x\)-axis have area \(A(x)\), then the volume is: \[ V=\int_a^b A(x)\,dx \] If a solid extends from \(y=a\) to \(y=b\) and the cross-sections perpendicular to the \(y\)-axis have area \(A(y)\), then the volume is: \[ V=\int_a^b A(y)\,dy \]
In practice, you do not need to go back to first principles as in the example. Rather you will need to work to find a formula for the cross-sectional area. Draw the base; draw a cross section; find the length of the base of the cross section and find the area of the cross section.
Here is another example in which the cross-sections are perpendicular to the \(y\)-axis.
Now you try some:
Find the volume of the solid whose base is the semicircle \(0 \le x \le \sqrt{9-y^2}\) and whose cross-sections perpendicular to the \(x\)-axis are rectangles whose height is half of the base.
Draw the base and one cross-section.
Here are the base with one cross-section and an accumulation of cross sections to form the final solid:
_rect_base.jpg)
one Cross Section
_rect_anim.gif)
and the Solid
\(V=36\)
See the second hint for pictures of the base with one cross-section and an accumulation of cross sections to form the final solid:
The equation of the circle is \(x^2+y^2=9\). The cross section sits on the base on the line segment from \(y_-=-\sqrt{9-x^2}\) to \(y_+=\sqrt{9-x^2}\). So its length is \(b=y_+-y_-=2\sqrt{9-x^2}\). The height is half the length, \(h=\dfrac{1}{2}b=\sqrt{9-x^2}\). So the cross-sectional area is \[ A=bh=2(9-x^2) \] and the volume is \[\begin{aligned} V&=\int_0^3 2(9-x^2)\,dx =2\left[9x-\dfrac{x^3}{3}\right]_0^3 \\[3pt] &=2(27-9)=36 \end{aligned}\]
Find the volume of the solid whose base is the circle \(x^2+y^2=4\), and whose cross-sections perpendicular to the \(x\)-axis are equilateral triangles.
Here are the base and a crosssection at position \(x\):
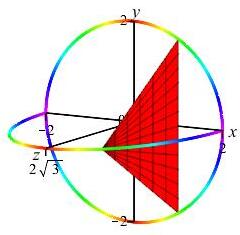
\(V=\dfrac{32}{3}\sqrt{3}\)
Here are the base with one cross-section and an accumulation of cross sections to form the final solid:

one Cross Section
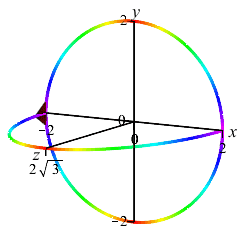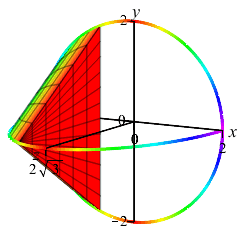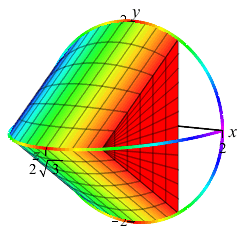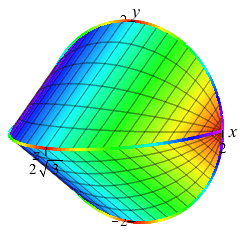
and the Solid
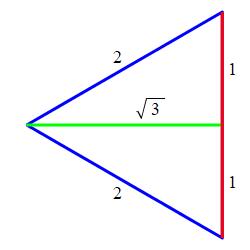
The circle is \(x^2+y^2=4\). So the endpoints of the base of the
triangle are at \(y_\pm=\pm\sqrt{4-x^2}\). So its length is
\(b=y_+-y_-=2\sqrt{4-x^2}\). The altitude is \(\sqrt{3}\) times half
the base: \(h=\sqrt{3}\sqrt{4-x^2}\).
(Think about the \(30^\circ-60^\circ-90^\circ\) which is half of an
equilateral triangle.)
So the area of the equilateral triangle is
\[\begin{aligned}
A&=\dfrac{1}{2}bh
=\dfrac{1}{2}2\sqrt{4-x^2}\sqrt{3}\sqrt{4-x^2} \\
&=\sqrt{3}(4-x^2)
\end{aligned}\]
Integrating this crosssectional area gives the volume: \[\begin{aligned} V&=\int_{-2}^2 A(x)\,dx =\int_{-2}^2 \sqrt{3}(4-x^2)\,dx \\ &=\sqrt{3}\left[ 4x-\dfrac{x^3}{3}\right]_{-2}^2 \\ &=\sqrt{3}\left[ 8-\dfrac{8}{3}\right]-\sqrt{3}\left[-8+\dfrac{8}{3}\right] =\dfrac{32}{3}\sqrt{3} \end{aligned}\]
You can practice computing Volumes by Slicing by using the following Maplet (requires Maple on the computer where this is executed):
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum