13. Volume
d1. Volume using Thin Washers
Next we consider the problem of computing the volume of a solid of revolution using thin washers.
The region between the functions \(y=f(x)\) and \(y=g(x)\) between \(x=a\) and \(x=b\) is rotated about the \(x\)-axis. Find the volume of the solid swept out.
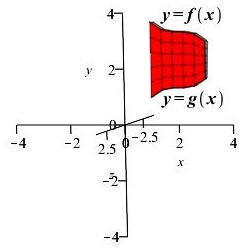
This is an \(x\) integral. So we draw a vertical rectangle and rotate it about the \(x\)-axis obtaining a thin washer.
The situation is exactly like the case for a disk except that we need to subtract off the volume of the hole. So the volume is: \[ V=\int_a^b (\pi f(x)^2-\pi g(x)^2)\,dx \]
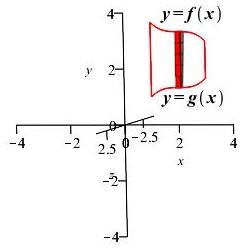
Now turn your head sideways:
![]()
The region between the functions \(x=f(y)\) and \(x=g(y)\) between \(y=a\) and \(y=b\) is rotated about the \(y\)-axis. Find the volume of the solid swept out.
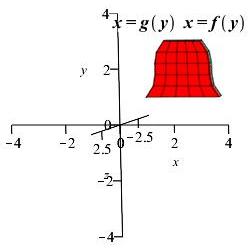
This is a \(y\) integral. So we draw a horizontal rectangle and rotate it about the \(y\)-axis obtaining a thin washer.
Again we subtract off the volume of the hole. So the volume is: \[ V=\int_a^b (\pi f(y)^2-\pi g(y)^2)\,dy \]
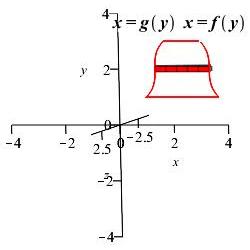
If the region below the function \(y=f(x)\) above the function \(y=g(x)\) between \(x=a\) and \(x=b\) is rotated about the \(x\)-axis, the volume swept out is: \[ V=\int_a^b \pi(f(x)^2-g(x)^2)\,dx \] If the region to the left of the function \(x=f(y)\) and to the right of the function \(x=g(y)\) between \(y=a\) and \(y=b\) is rotated about the \(y\)-axis, the volume swept out is: \[ V=\int_a^b \pi(f(y)^2-g(y)^2)\,dy \] Both formulas can be summarized as \[ V=\int_a^b \pi(\text{outer radius})^2-\pi(\text{inner radius})^2\,dv \] where \(dv\) is either \(dx\) or \(dy\).
Notice that finding the volume of a solid of revolution by washers is really a special case of finding a volume by slicing \[ V=\int_a^b A(v)\,dv \] in which each cross-sectional area is the area between two circles, \(A=\pi(\text{outer radius})^2-\pi(\text{inner radius})^2\).
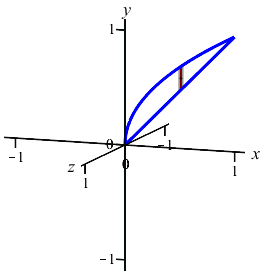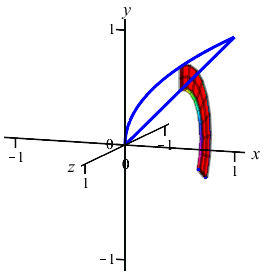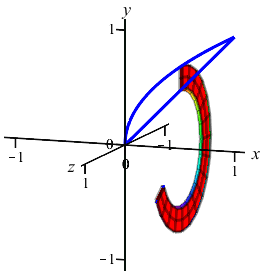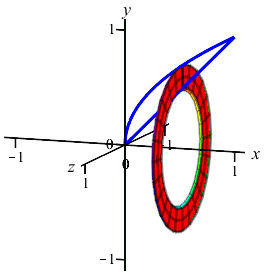
The area between the curves \(y=x\) and \(y=\sqrt{x}\) can be computed as either an \(x\)-integral or as a \(y\)-integral. It can also be rotated about the \(x\)-axis or about the \(y\)-axis. We will look at all four possibilities on this and the next page.
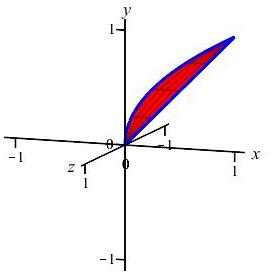
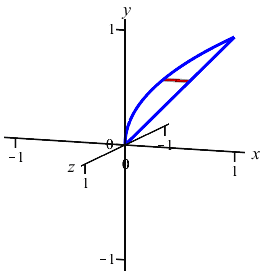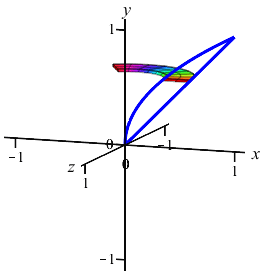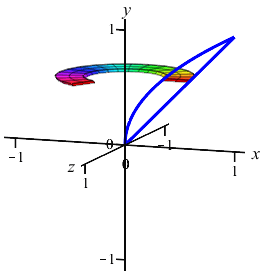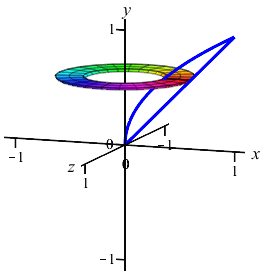
The region between the curves \(x=y\) and \(x=y^2\) is rotated about the \(y\)-axis. Find the volume swept out. (Do the integral as a \(y\) integral.)
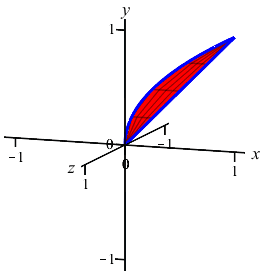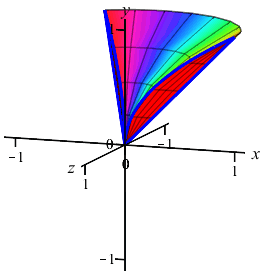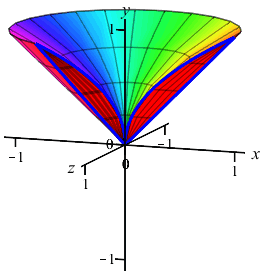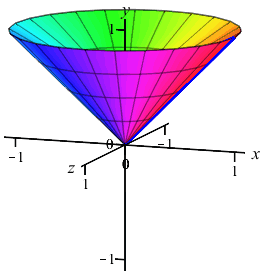
Since the curves are given with \(x\) as functions of \(y\), we will compute using a \(y\)-integral. We cut up the \(y\)-axis and see that the rectangles are horizontal and rotate into thin washers. So the volume is: \[\begin{aligned} V&=\pi\int_a^b (\text{right}^2-\text{left}^2)\,dy =\pi\int_0^1 ((y)^2-(y^2)^2)\,dy \\ &=\pi\int_0^1 (y^2-y^4)\,dy =\pi\left[\dfrac{y^3}{3}-\dfrac{y^5}{5}\right]_0^1 =\dfrac{2}{15}\pi \end{aligned}\]
Now it's your turn:
The region between the curves \(y=x\) and \(y=\sqrt{x}\) is rotated about the \(x\)-axis. Find the volume swept out. (Do the integral as an \(x\) integral.)
Notice this is the same \(2\)-dimensional area as in example 1, but it is rotated about a different axis. So the volume is totally different.
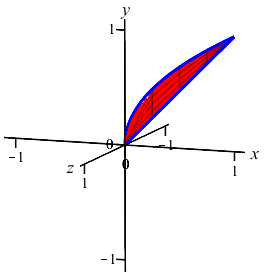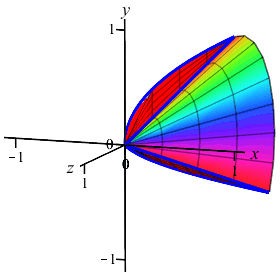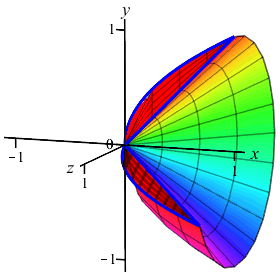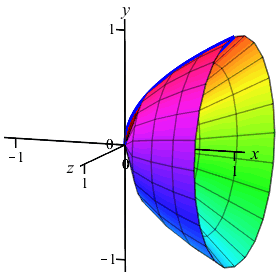
The volume is to be computed as an \(x\)-integral. So cut up the \(x\)-axis.
\(\displaystyle V=\dfrac{\pi}{6}\)
We cut up the \(x\)-axis and see that the rectangles are vertical and they rotate into thin washers. So the volume is: \[\begin{aligned} V&=\pi\int_a^b (\text{upper}^2-\text{lower}^2)\,dx \\ &=\pi\int_0^1 \left((\sqrt{x})^2-(x)^2\right)\,dx \\ &=\pi\int_0^1 (x-x^2)\,dx =\pi\left[\dfrac{x^2}{2}-\dfrac{x^3}{3}\right]_0^1=\dfrac{\pi}{6} \end{aligned}\]
Here's another example:
| Example |
You can practice computing Volumes of Revolution by Disks and Washers by using the following Maplet (requires Maple on the computer where this is executed):
Volume of a Solid of Revolution Rate It
For now, when you click on Show in Step 1, only do those problems which are Disks or Washers.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum