13. Volume

b2. Volumes of Revolution: Disks, Washers or Cylinders?

When we need to compute the volume of a solid of revolution, we will need to decide whether to do an \(x\) integral or a \(y\) integral and whether to use disks, washers or cylinders. Do not simply try to remember all the formulas for the appropriate cases. Rather, here are several steps to follow to help make these decisions.

  1. Draw the region in the \(xy\)-plane.
  2. Decide if we will do an \(x\)-integral or a \(y\)-integral.

    3. This decision should be made in exactly the same way we would decide how to compute the area of the region, without regard to the axis of rotation. Is it easier to compute the area as an \(x\) integral or as a \(y\) integral? Do the same for the volume.

  3. Determine the limits for the integral.

    4. We do this exactly as we would for computing the area.

  4. Draw one Riemann sum rectangle in the figure.

    5. For an \(x\)-integral the rectangle is vertical. For a \(y\)-integral the rectangle is horizontal.

  5. Rotate the rectangle about the specified axis and observe if it sweeps out a disk, a washer or a cylinder.

On the next three pages we will discuss the volume integrals in each of the three cases. But first some examples and exercises.

The region between the parabola \(y=4x-x^2\) and the line \(y=x\) is rotated about the \(x\)-axis. To find the volume swept out, should we do an \(x\) or \(y\) integral? What is the interval of integration? Is a Riemann sum rectangle horizontal or vertical? Does the Riemann sum rectangle sweep out a disk, washer of cylinder?

eg_4x_x-x^2_x_crv

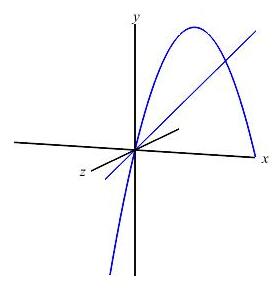
The boundaries of the region are given with \(y\) as functions of \(x\). So we should do an \(x\) integral. (Further, if we tried to do it as a \(y\) integral, we would need to split the integral at \(y=3\).) To find the limits of integration, we equate the functions: \[\begin{aligned} 4x-x^2=x \quad &\Rightarrow& \quad 0&=x^2-3x=x(x-3) \\ \quad &\Rightarrow& \quad x&=0,3 \end{aligned}\] Since this is an \(x\) integral, we add a vertical Riemann sum rectangle to the plot, rotate it about the \(x\)-axis and observe it sweeps out a washer.

eg_4x_x-x^2_x_about_x_anim

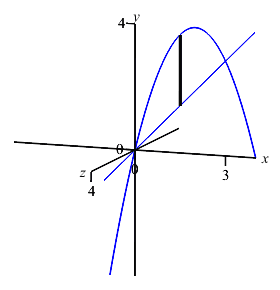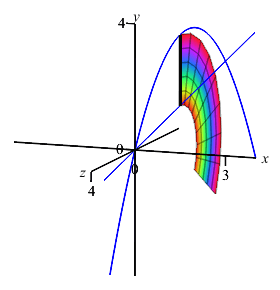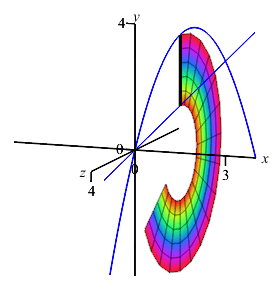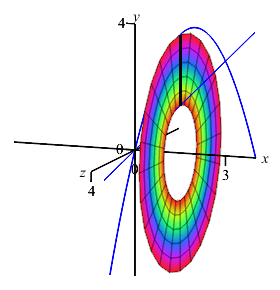
We now rotate the same region about the opposite axis.

The region between the parabola \(y=4x-x^2\) and the line \(y=x\) is rotated about the \(y\)-axis. To find the volume swept out, should we do an \(x\) or \(y\) integral? What is the interval of integration? Is a Riemann sum rectangle horizontal or vertical? Does the Riemann sum rectangle sweep out a disk, washer of cylinder?

eg_4x_x-x^2_x_crv

The boundaries of the region are given with \(y\) as functions of \(x\). So we should still do an \(x\) integral. The limits of integration are still \(x=0,3\). Since this is an \(x\) integral, we still add a vertical Riemann sum rectangle to the plot. However, when we rotate it about the \(y\)-axis, it now sweeps out a cylinder.

eg_4x_x-x^2_x_about_y_anim

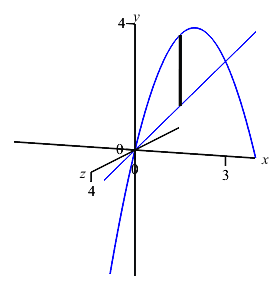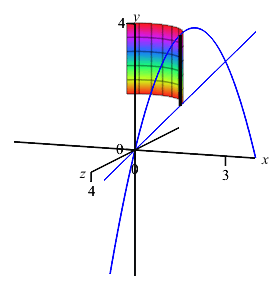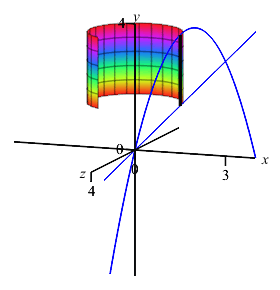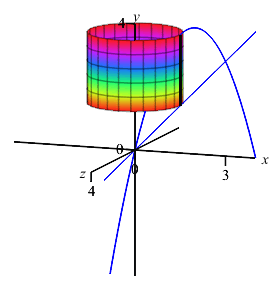
Now you try.

The region between the parabola \(x=y^2\) and the \(y\)-axis for \(0 \le y \le 3\) is rotated about the \(x\)-axis. To find the volume swept out, should we do an \(x\) or \(y\) integral? What is the interval of integration? Is a Riemann sum rectangle horizontal or vertical? Does the Riemann sum rectangle sweep out a disk, washer of cylinder?

ex_y^2_0-3_crv

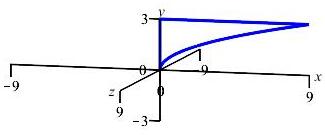
If we were going to find the area, would we do an \(x\) or \(y\) integral? Would a Riemann sum rectangle be horizontal or vertical?

We do a \(y\) integral on \(0 \le y \le 3\).
A Riemann sum rectangle is horizontal and sweeps out a cylinder.

The boundaries of the region are given with \(x\) as functions of \(y\). So we should do an \(y\) integral. The interval of integration is \(0 \le y \le 3\). Since this is an \(y\) integral, we add a horizontal Riemann sum rectangle to the plot, rotate it about the \(x\)-axis and observe it sweeps out a cylinder.

ex_y^2_0-3_about_x_anim

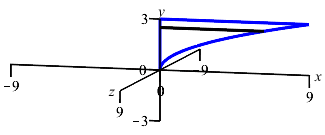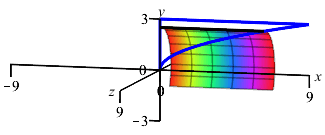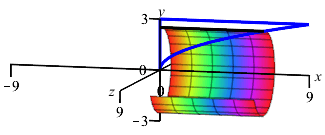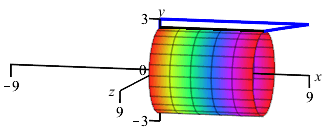
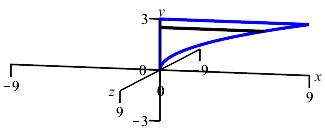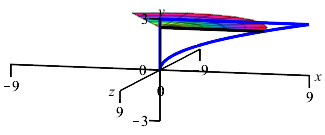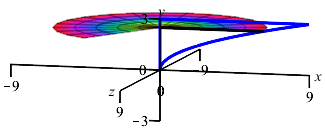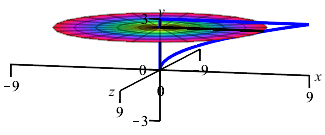
The region between the parabola \(x=y^2\) and the \(y\)-axis for \(0 \le y \le 3\) is rotated about the \(y\)-axis. To find the volume swept out, should we do an \(x\) or \(y\) integral? What is the interval of integration? Is a Riemann sum rectangle horizontal or vertical? Does the Riemann sum rectangle sweep out a disk, washer of cylinder?

ex_y^2_0-3_crv

If we were going to find the area, would we do an \(x\) or \(y\) integral? Would a Riemann sum rectangle be horizontal or vertical?

We do a \(y\) integral on \(0 \le y \le 3\).
A Riemann sum rectangle is horizontal and sweeps out a disk.

We still do an \(y\) integral on \(0 \le y \le 3\). Since this is an \(y\) integral, we still add a horizontal Riemann sum rectangle. However, when we rotate it about the \(y\)-axis, it now sweeps out a disk.

ex_y^2_0-3_about_y_anim
PY: We need to add a discussion of rotating about axes other than the x-axis or the y-axis.

© MYMathApps

Supported in part by NSF Grant #1123255