10. Riemann Sums, Integrals and the FTC

Exercises

a. Definition of Riemann Sums

Use a Riemann sum with \(3\) equal width intervals and right endpoints to approximate the area below \(y=\dfrac{1}{x}\) above the \(x\)-axis between \(x=2\) and \(x=8\).

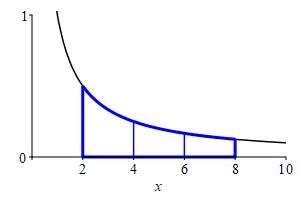
The area is the integral \(\displaystyle A=\int_2^8 \dfrac{1}{x}\,dx\) which may be approximated by the Riemann Sum \(\displaystyle R_3=\sum_{i=1}^3 f(x_i)\Delta x\).

\(\displaystyle A=\int_2^8 \dfrac{1}{x}\,dx \approx R_3=\dfrac{13}{12}\approx1.083\)

We divide the interval \([a,b]=[2,8]\) into \(n=3\) subintervals of equal width: \[ \Delta x=\dfrac{b-a}{n}=\dfrac{8-2}{3}=2 \] The right endpoints are: \[ x_1=4 \qquad x_2=6 \qquad x_3=8 \]

and the values of the function \(f(x)=\dfrac{1}{x}\) are: \[ f(4)=\dfrac{1}{4} \qquad f(6)=\dfrac{1}{6} \qquad f(8)=\dfrac{1}{8} \] So the Riemann sum is: \[\begin{aligned} R_3&=\sum_{i=1}^3 f(x_i)\Delta x \\ &=\left(\dfrac{1}{4}+\dfrac{1}{6}+\dfrac{1}{8}\right)2 =\dfrac{13}{12}\approx1.083 \end{aligned}\]

bl

Use a right Riemann sum (a Riemann sum with equal width intervals and right endpoints) with \(6\) intervals to approximate the area below \(y=\sin\theta\) above the \(\theta\)-axis between \(\theta=0\) and \(\theta=\pi\).

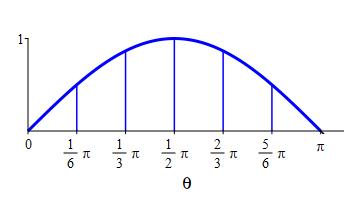
The area is the integral \(\displaystyle A=\int_0^\pi \sin\theta\,d\theta\) which may be approximated by the Riemann Sum \(\displaystyle R_6=\sum_{i=1}^6 f(\theta _i)\Delta \theta\).

\(\displaystyle A=\int_0^\pi \sin\theta\,d\theta \approx R_6=\dfrac{2+\sqrt{3}}{6}\pi \approx 1.95 \)

We divide the interval \([a,b]=[0,\pi]\) into \(n=6\) subintervals of equal width: \[ \Delta \theta=\dfrac{b-a}{n}=\dfrac{\pi -0}{6}=\dfrac{\pi}{6} \] The right endpoints are: \[\begin{aligned} \theta_1&=\dfrac{\pi}{6} & \theta_2&=\dfrac{\pi}{3} & \theta_3&=\dfrac{\pi}{2} \\ \theta_4&=\dfrac{2\pi}{3}\quad & \theta_5&=\dfrac{5\pi}{6}\quad & \theta_6&=\pi \end{aligned}\] and the values of the function \(f(\theta)=\sin\theta\) are: \[\begin{aligned} f(\theta_1)&=\dfrac{1}{2} & f(\theta_2)&=\dfrac{\sqrt{3}}{2}\quad & f(\theta_3)&=1 \\ f(\theta_4)&=\dfrac{\sqrt{3}}{2}\quad & f(\theta_5)&=\dfrac{1}{2} & f(\theta_6)&=0 \end{aligned}\]

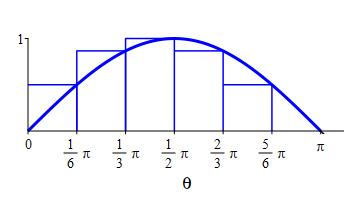
So the Riemann sum is: \[\begin{aligned} R_6&=\sum_{i=1}^6 f(\theta_i)\Delta \theta \\ &=\left(\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}+1 +\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}+0\right)\dfrac{\pi}{6} \\ &=\dfrac{2+\sqrt{3}}{6}\pi \approx 1.95 \end{aligned}\]

bl
Use a midpoint Riemann sum with \(4\) intervals to approximate the integral \(\displaystyle \int_{-4}^4 x^2-4\,dx\).

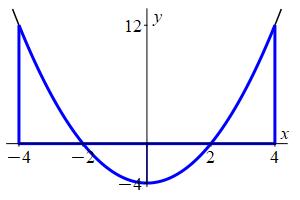
The integral \(\displaystyle \int_{-4}^4 x^2-4\,dx\) may be approximated by the Riemann Sum \(\displaystyle M_4=\sum_{i=1}^4 f(x_i^*)\Delta x\) where the \(x_i^*\) are the midpoints of each interval.

\(\displaystyle \int_{-4}^4 x^2-4\,dx\approx M_4=8 \)

We divide the interval \([a,b]=[-4,4]\) into \(n=4\) subintervals of equal width: \[ \Delta x=\dfrac{b-a}{n}=\dfrac{4-(-4)}{4}=2 \] The midpoints are: \[ x_1^*=-3 \qquad x_2^*=-1 \qquad x_3^*=1 \qquad x_4^*=3 \] and the values of the function \(f(x)=x^2-4\) are:

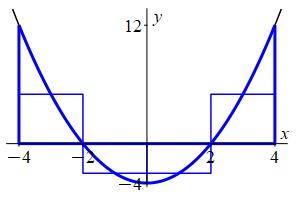
\[ f(-3)=5 \quad f(-1)=-3 \quad f(1)=-3 \quad f(3)=5 \] So the Riemann sum is: \[\begin{aligned} M_4&=\sum_{i=1}^4 f(x_i^*)\Delta x \\ &=(5-3-3+5)2 =8 \end{aligned}\] This is a much better approximation than a left or right Riemann sum.

bl

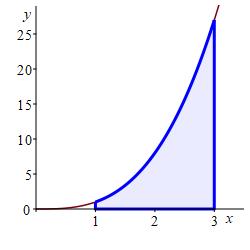
In a previous example, we approximated the area below \(y=x^3\) above the \(x\)-axis between \(x=1\) and \(x=3\) using a Riemann sum with \(4\) equal width intervals and right endpoints. Now approximate it using Riemann sums with \(4\) equal width intervals and:
1. left endpoints.
  
  \(\displaystyle A=\int_1^3 x^3\,dx\approx L_4=14.0 \)
  
  We divide the interval \([a,b]=[1,3]\) into \(n=4\) subintervals of equal width: \[ \Delta x=\dfrac{b-a}{n}=\dfrac{3-1}{4}=\dfrac{1}{2} \] The left endpoints are: \[\begin{aligned} x_1=1 \qquad x_2=\dfrac{3}{2} \qquad x_3=2 \qquad x_4=\dfrac{5}{2} \end{aligned}\] and the values of the function \(f(x)=x^3\) are:
  
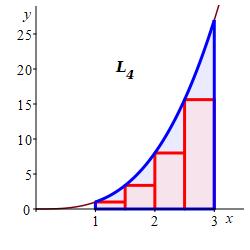
  \[\begin{aligned} f(x_1)=1 \qquad f(x_2)=\dfrac{27}{8} \qquad f(x_3)=8 \qquad f(x_4) =\dfrac{125}{8} \end{aligned}\] So the left Riemann sum is: \[\begin{aligned} L_4&=\sum_{i=1}^4 f(x_i)\Delta x \\ &=\left(1+\dfrac{27}{8}+8+\dfrac{125}{8}\right)\dfrac{1}{2} =14.0 \end{aligned}\]
2. midpoints.
  
  \(\displaystyle A=\int_1^3 x^3\,dx\approx M_4=\dfrac{79}{4}=19.75 \)
  
  We divide the interval \([a,b]=[1,3]\) into \(n=4\) subintervals of equal width: \[ \Delta x=\dfrac{b-a}{n}=\dfrac{3-1}{4}=\dfrac{1}{2} \] The midpoints are: \[\begin{aligned} x_1=\dfrac{5}{4} \qquad x_2&=\dfrac{7}{4} \qquad x_3=\dfrac{9}{4} \qquad x_4=\dfrac{11}{4} \end{aligned}\] and the values of the function \(f(x)=x^3\) are:
  
  \[\begin{aligned} f(x_1)=\dfrac{125}{64} \qquad f(x_2)=\dfrac{343}{64} \qquad f(x_3)=\dfrac{729}{64} \qquad f(x_4)=\dfrac{1331}{64} \end{aligned}\] So the middle Riemann sum is: \[\begin{aligned} M_4&=\sum_{i=1}^4 f(x_i)\Delta x \\ &=\left(\dfrac{125}{64}+\dfrac{343}{64}+\dfrac{729}{64} +\dfrac{1331}{64}\right)\dfrac{1}{2} =\dfrac{79}{4}=19.75 \end{aligned}\]
  
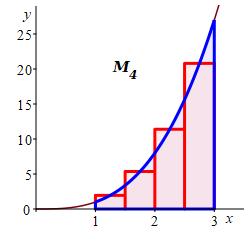
  Here are the plots of the left, middle and right Riemann sums along with their values:
  
  \(L_4=14.0\)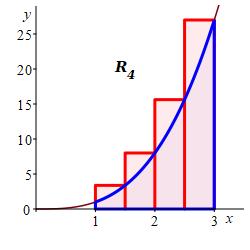
  
  \(R_4=27.0\)
  
  \(M_4=19.75\)
  
  We will see eventually that the actual area is \(A=20\).
  
  The plots together with the fact that \(x^3\) is increasing, explain why the left sum is an underestimate, the right sum is an overestimate and the middle sum is a much better estimate. This is a case of Papa Bear, Momma Bear and Baby Bear.
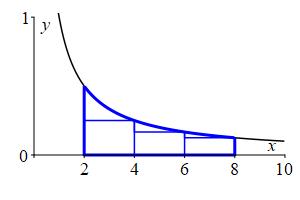
In a previous exercise, we approximated the area below \(y=\dfrac{1}{x}\) above the \(x\)-axis between \(x=2\) and \(x=8\) using a Riemann sum with \(3\) equal width intervals and right endpoints. Now approximate it using Riemann sums with \(3\) equal width intervals and:
1. left endpoints.
  
  \(\displaystyle A=\int_2^8 \dfrac{1}{x}\,dx\approx L_3=\dfrac{11}{6}\approx1.83 \)
  
  We divide the interval \([a,b]=[2,8]\) into \(n=3\) subintervals of equal width: \[ \Delta x=\dfrac{b-a}{n}=\dfrac{8-2}{3}=2 \] The left endpoints are: \[\begin{aligned} x_1=2 \qquad x_2=4 \qquad x_3=6 \end{aligned}\] and the values of the function \(f(x)=\dfrac{1}{x}\) are:
  
  \[\begin{aligned} f(x_1)=\dfrac{1}{2} \qquad f(x_2)=\dfrac{1}{4} \qquad f(x_3)=\dfrac{1}{6} \end{aligned}\] So the left Riemann sum is: \[\begin{aligned} L_3&=\sum_{i=1}^3 f(x_i)\Delta x \\ &=\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}\right)2 =\dfrac{11}{6}\approx1.83 \end{aligned}\]
2. midpoints.
  
  \(\displaystyle A=\int_2^8 \dfrac{1}{x}\,dx\approx M_3=\dfrac{142}{105}\approx1.35 \)
  
  We divide the interval \([a,b]=[2,8]\) into \(n=3\) subintervals of equal width: \[ \Delta x=\dfrac{b-a}{n}=\dfrac{8-2}{3}=2 \] The midpoints are: \[ x_1=3 \qquad x_2=5 \qquad x_3=7 \] and the values of the function \(f(x)=\dfrac{1}{x}\) are:
  
  \[\begin{aligned} f(x_1)=\dfrac{1}{3} \qquad f(x_2)=\dfrac{1}{5} \qquad f(x_3)=\dfrac{1}{7} \end{aligned}\] So the middle Riemann sum is: \[\begin{aligned} M_3&=\sum_{i=1}^3 f(x_i)\Delta x \\ &=\left(\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}\right)2 =\dfrac{142}{105}\approx1.35 \end{aligned}\]
  
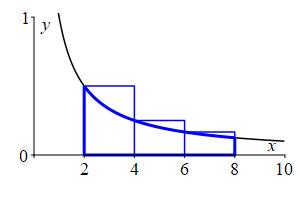
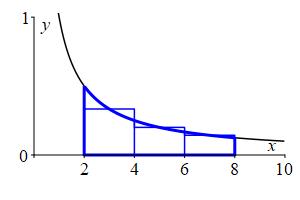
  Here are the plots of the left, right and middle Riemann sums along with their values:
  
  \(L_3\approx1.83\)
  
  \(R_3\approx1.083\)
  
  \(M_3\approx1.35\)
  
  We will see eventually that the actual area is \(A=2\ln2\approx1.39\).
  
  The plots together with the fact that \(\dfrac{1}{x}\) is decreasing, explain why the left sum is an overestimate, the right sum is an underestimate and the middle sum is a much better estimate. Again, Papa Bear, Momma Bear, Baby Bear. However, this time the function was decreasing, and so which of the left or right Rieman Sum is the underestimate and which is the overestimate reverses.

Approximate the integral \(\displaystyle \int_0^6 (3x^2-12x-5)\,dx\) using a Riemann sum with \(3\) equal width intervals and:
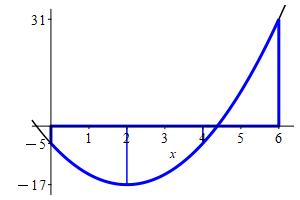
1. left endpoints.
  
  \(\displaystyle \int_0^6 3x^2-12x-5\,dx\approx L_3=-54 \)
  
  We divide the interval \([a,b]=[0,6]\) into \(n=3\) subintervals of equal width: \[ \Delta x=\dfrac{b-a}{n}=\dfrac{6-0}{3}=2 \] The left endpoints are: \[\begin{aligned} x_1=0 \qquad x_2=2 \qquad x_3=4 \end{aligned}\] and values of the function \(f(x)=3x^2-12x-5\) are:
  
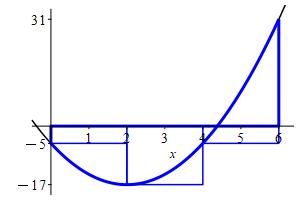
  \[\begin{aligned} f(x_1)=-5 \qquad f(x_2)=-17 \qquad f(x_3)=-5 \end{aligned}\] So the left Riemann sum is: \[\begin{aligned} L_3&=\sum_{i=1}^3 f(x_i)\Delta x \\ &=(-5-17-5))2 =-54 \end{aligned}\]
  
  rm,jr
2. right endpoints.
  
  \(\displaystyle \int_0^6 3x^2-12x-5\,dx\approx R_3=18 \)
  
  We divide the interval \([a,b]=[0,6]\) into \(n=3\) subintervals of equal width: \[ \Delta x=\dfrac{b-a}{n}=\dfrac{6-0}{3}=2 \] The right endpoints are: \[\begin{aligned} x_1=2 \qquad x_2=4 \qquad x_3=6 \end{aligned}\] and values of the function \(f(x)=3x^2-12x-5\) are:
  
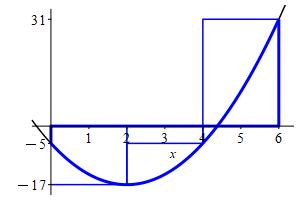
  \[\begin{aligned} f(x_1)=-17 \qquad f(x_2)=-5 \qquad f(x_3)=31 \end{aligned}\] So the right Riemann sum is: \[\begin{aligned} R_3&=\sum_{i=1}^3 f(x_i)\Delta x \\ &=(-17-5+31)2 =18 \end{aligned}\]
  
  rm,jr
3. midpoints.
  
  \(\displaystyle \int_0^6 3x^2-12x-5\,dx\approx M_3=-36 \)
  
  We divide the interval \([a,b]=[0,6]\) into \(n=3\) subintervals of equal width: \[ \Delta x=\dfrac{b-a}{n}=\dfrac{6-0}{3}=2 \] The midpoints are: \[\begin{aligned} x_1=1 \qquad x_2=3 \qquad x_3=5 \end{aligned}\] and values of the function \(f(x)=3x^2-12x-5\) are:
  
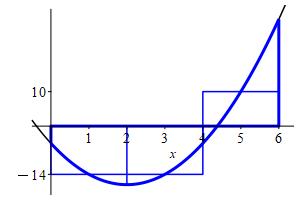
  \[\begin{aligned} f(x_1)=-14 \qquad f(x_2)=-14 \qquad f(x_3)=10 \end{aligned}\] So the middle Riemann sum is: \[\begin{aligned} M_3&=\sum_{i=1}^3 f(x_i)\Delta x \\ &=(-14-14+10)2 =-36 \end{aligned}\]
  
  rm,jr

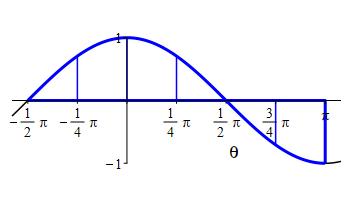
Approximate the integral \(\displaystyle \int_{-\pi/2}^{\pi} \cos\theta\,d\theta\) using:
1. a right Riemann sum with \(6\) intervals.
  
  \(\displaystyle \int_{-\pi/2}^{\pi} \cos\theta\,d\theta\,\approx R_6= \dfrac{\sqrt{2} \pi}{8} \approx 0.56 \)
  
  We divide the interval \(a=-\dfrac{\pi}{2}\) and \(b=\pi\) into \(n=6\) subintervals of equal width: \[ \Delta\theta=\dfrac{b-a}{n}=\dfrac{\pi -(-\dfrac{\pi}{2})}{6} =\dfrac{\pi}{4} \] The right endpoints are: \[\begin{aligned} \theta_1&=-\dfrac{\pi}{4} & \theta_2&=0 & \theta_3&=\dfrac{\pi}{4}\\ \theta_4&=\dfrac{\pi}{2} & \theta_5&=\dfrac{3\pi}{4} & \theta_6&=\pi\\ \end{aligned}\] and the values of the the function, \(f(\theta)=\cos(\theta)\), are:
  
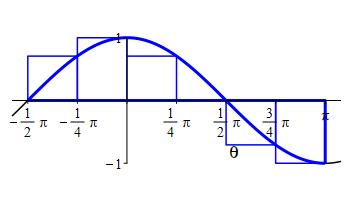
  \[\begin{aligned} f(\theta_1)&=\dfrac{\sqrt{2}}{2} & f(\theta_2)&=1 & f(\theta_3) &=\dfrac{\sqrt{2}}{2}\\ f(\theta_4)&=0 & f(\theta_5)&=-\dfrac{\sqrt{2}}{2} & f(\theta_6) &=-1 \end{aligned}\] So the Riemann sum is: \[\begin{aligned} R_6&=\sum_{i=1}^6 f(\theta_i)\Delta \theta \\ &=\left(\dfrac{\sqrt{2}}{2}+1+\dfrac{\sqrt{2}}{2}+0 -\dfrac{\sqrt{2}}{2}-1\right)\dfrac{\pi}{4} =\dfrac{\sqrt{2} \pi}{8} \approx 0.56 \end{aligned}\]
2. a left Riemann sum with \(6\) intervals.
  
  \(\displaystyle \int_{-\pi/2}^{\pi} \cos\theta\,d\theta\approx R_6 =\dfrac{\pi}{4}\left(1+\dfrac{\sqrt{2}}{2}\right) \approx 1.34 \)
  
  We divide the interval \(a=-\dfrac{\pi}{2}\) and \(b=\pi\) into \(n=6\) subintervals of equal width: \[ \Delta\theta=\dfrac{b-a}{n}=\dfrac{\pi -(-\dfrac{\pi}{2})}{6} =\dfrac{\pi}{4} \] The left endpoints are: \[\begin{aligned} \theta_1&=-\dfrac{\pi}{2} & \theta_2&=-\dfrac{\pi}{4} & \theta_3&=0\\ \theta_4&=\dfrac{\pi}{4} & \theta_5&=\dfrac{\pi}{2} & \theta_6 &=\dfrac{3\pi}{4}\\ \end{aligned}\] and the values of the the function, \(f(x)=\cos(\theta)\), are:
  
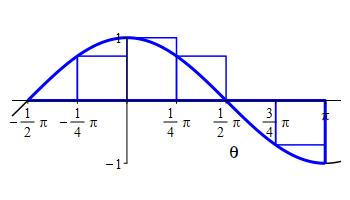
  \[\begin{aligned} f(\theta_1)&=0 & f(\theta_2)&=\dfrac{\sqrt{2}}{2} & f(\theta_3) &=1\\ f(\theta_4)&=\dfrac{\sqrt{2}}{2} & f(\theta_5)&=0 & f(\theta_6) &=-\dfrac{\sqrt{2}}{2}\\ \end{aligned}\] So the Riemann sum is: \[\begin{aligned} R_6&=\sum_{i=1}^6 f(\theta_i)\Delta \theta \\ &=\left(0+\dfrac{\sqrt{2}}{2}+1+\dfrac{\sqrt{2}}{2}+0-\dfrac{\sqrt{2}}{2}\right)\dfrac{\pi}{4} =\dfrac{\pi}{4}\left(1+\dfrac{\sqrt{2}}{2}\right) \approx 1.34 \end{aligned}\]

Use a limit of Riemann sums to find the area below \(y=x^3\) above the \(x\)-axis between \(x=1\) and \(x=3\).

The right endpoints are \(x_i=1+i\Delta x\). Evaluate the function \(f(x)=x^3\) at the right endpoints and compute the limit of the sum.

\(\displaystyle A=\int_1^3 x^3\,dx=20\)

The area is \(\displaystyle A=\int_1^3 x^3\,dx\) which we compute as a limit of Riemann sums. We split the interval \([1,3]\) into \(n\) equal parts of width: \[ \Delta x=\dfrac{3-1}{n}=\dfrac{2}{n} \] Then the right endpoints are: \[ x_i=1+i\Delta x=1+\dfrac{2}{n}i \] Since the integrand is the function \(f(x)=x^3\), its value at the right endpoints are: \[\begin{aligned} f(x_i)&=(x_i)^3=\left(1+\dfrac{2}{n}i\right)^3 \\ &=1+3\dfrac{2}{n}i+3\dfrac{2^2}{n^2}i^2+\dfrac{2^3}{n^3}i^3 \\ &=1+\dfrac{6}{n}i+\dfrac{12}{n^2}i^2+\dfrac{8}{n^3}i^3 \end{aligned}\] We set up the Riemann sum, expand each term, write it as a sum of summations and factor out the coefficients: \[\begin{aligned} \sum_{i=1}^n &f(x_i)\Delta x =\sum_{i=1}^n \left(1+\dfrac{2}{n}i\right)^3\dfrac{2}{n} \\ &=\sum_{i=1}^n \left(1+\dfrac{6}{n}i+\dfrac{12}{n^2}i^2+\dfrac{8}{n^3}i^3\right) \dfrac{2}{n} \\ &=\sum_{i=1}^n \left(\dfrac{2}{n}+\dfrac{12}{n^2}i +\dfrac{24}{n^3}i^2+\dfrac{16}{n^4}i^3\right) \\ &=\sum_{i=1}^n \dfrac{2}{n}+\sum_{i=1}^n \dfrac{12}{n^2}i +\sum_{i=1}^n \dfrac{24}{n^3}i^2+\sum_{i=1}^n \dfrac{16}{n^4}i^3 \\ &=\dfrac{2}{n}\sum_{i=1}^n 1+\dfrac{12}{n^2}\sum_{i=1}^n i +\dfrac{24}{n^3}\sum_{i=1}^n i^2+\dfrac{16}{n^4}\sum_{i=1}^n i^3 \\ \end{aligned}\] We now use the basic summations and simplify: \[\begin{aligned} &\qquad \sum_{i=1}^n f(x_i)\Delta x \\ &=\dfrac{2}{n}\cdot n+\dfrac{12}{n^2}\cdot\dfrac{n(n+1)}{2} +\dfrac{24}{n^3}\cdot\dfrac{n(n+1)(2n+1)}{6} +\dfrac{16}{n^4}\cdot\dfrac{n^2(n+1)^2}{4} \\ &=2+6\dfrac{(n+1)}{n} +4\dfrac{(n+1)(2n+1)}{n^2} +4\dfrac{(n+1)^2}{n^2} \\ \end{aligned}\] Finally, we compute the integral as the limit of this Riemann sum: \[\begin{aligned} A&=\int_1^3 x^3\,dx =\lim_{n\to\infty}\sum_{i=1}^n f(x_i)\Delta x \\ &=\lim_{n\to\infty}\left(2+6\dfrac{(n+1)}{n} +4\dfrac{(n+1)(2n+1)}{n^2}+4\dfrac{(n+1)^2}{n^2}\right) \\ &=2+6+8+4=20 \end{aligned}\] Be careful with the third term which has a \(2\) in the formula for the sum.

The integral was approximated by a right Riemann sum in a previous example. It was also approximated by left and middle Riemann sums in an exercise above. The values were: \[ L_4=14.0 \qquad M_4=19.75 \qquad R_4=27.0 \] The correct area is \(A=20\). So the middle Riemann sum is the best of these approximations.

Use a limit of Riemann sums to compute the integral \(\displaystyle \int_0^6 (3x^2-12x-5)\,dx\).

The right endpoints are \(x_i=i\Delta x\) since \(a=0\). Evaluate the function at the right endpoints and compute the limit of the sum.

\(\displaystyle \int_0^6 3x^2-12x-5\,dx=-30\)

The integral is \(\displaystyle \int_0^6 3x^2-12x-5\,dx\) which we compute as a limit of Riemann sums. We split the interval \([0,6]\) into \(n\) equal parts of width: \[ \Delta x=\dfrac{b-a}{n}=\dfrac{6-0}{n}=\dfrac{6}{n} \] Then the right endpoints are: \[ x_i=a+i\Delta x=\dfrac{6}{n}i \] The values of the integrand, \(f(x)=3x^2-12x-5\), at the right endpoints are: \[\begin{aligned} f(x_i)&=3(x_i)^2-12(x_i)-5 =3\left(\dfrac{6}{n}i\right)^2-12\left(\dfrac{6}{n}i\right)-5 \\ &=\dfrac{108}{n^2}i^2-\dfrac{72}{n}i-5 \end{aligned}\] We set up the Riemann sum, expand each term, write it as a sum of summations and factor out the coefficients: \[\begin{aligned} \sum_{i=1}^n &f(x_i)\Delta x =\sum_{i=1}^n \left(\dfrac{108}{n^2}i^2-\dfrac{72}{n}i-5\right)\dfrac{6}{n} \\ &=\dfrac{648}{n^3}\sum_{i=1}^n i^2-\dfrac{432}{n^2}\sum_{i=1}^n i-\dfrac{30}{n}\sum_{i=1}^n 1 \end{aligned}\] We now use the basic summations and simplify: \[\begin{aligned} \sum_{i=1}^n f(x_i)\Delta x &=\dfrac{648}{n^3}\dfrac{n(n+1)(2n+1)}{6}-\dfrac{432}{n^2}\dfrac{n(n+1)}{2}-\dfrac{30}{n}(n) \\ &=108\dfrac{(n+1)(2n+1)}{n^2}-216\dfrac{(n+1)}{n}-30 \end{aligned}\] Finally, we compute the integral as the limit of this Riemann sum: \[\begin{aligned} \int_0^6 &3x^2-12x-5\,dx =\lim_{n\to\infty}\sum_{i=1}^n f(x_i)\Delta x \\ &=\lim_{n\to\infty}\left(108\dfrac{(n+1)(2n+1)}{n^2}-216\dfrac{(n+1)}{n}-30\right) \\ &=216-216-30=-30 \end{aligned}\]

rm,jr

This integral was approximated by left, right and middle Riemann sums in an exercise above. The plots and values were:

\(L_3=-54\)

\(R_3=18\)

\(M_3=-36\)

The value of the integral is \(\displaystyle \int_0^6 3x^2-12x-5\,dx=-30\). So the middle Riemann sum is the best of these approximations even though the function is neither increasing nor decreasing. That is because it is the best on each interval where it is increasing or decreasing.
Compute \(\displaystyle \int_0^9 f(x)\,dx\) for the function \(f(x)\) shown, which consists of two straight lines and a quarter circle.

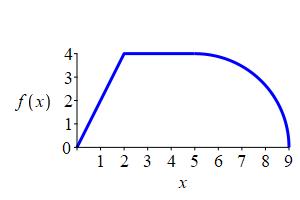
\(\displaystyle A=16+4\pi\)

The integral gives the area under the curve.
The area below the curve above \([0,2]\) is a triangle, so its area is: \[ A=\dfrac{1}{2}(\text{base})(\text{height})=\dfrac{1}{2}\cdot2\cdot4=4 \]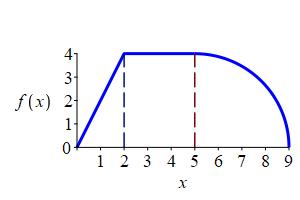

The area below the curve above \([2,5]\) is a rectangle, so its area is: \[ A=(\text{base})(\text{height})=3\cdot4=12 \] The area below the curve above \([5,9]\) is a quarter circle, so its area is: \[ A=\dfrac{1}{4}\pi r^2=\dfrac{1}{4}\pi4^2=4\pi \] So, the interval is \[ \int_0^9 f(x)\,dx=4+12+4\pi=16+4\pi \]
Compute \(\displaystyle \int_2^{12} g(x)\,dx\) for the function \(g(x)\) shown. The blue curve is a semicircle.

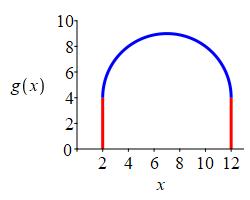
\(\displaystyle A=40+\dfrac{25}{2}\pi\)

The integral gives the area under the curve.
The region is a semicircle above a rectangle.
The area of the rectangle is: \[ A=(\text{base})(\text{height})=10\cdot4=40 \]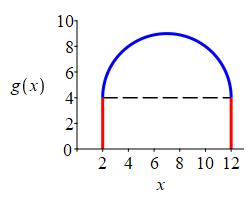

The area of the semi-circle is: \[ A=\dfrac{1}{2}\pi r^2=\dfrac{1}{2}\pi5^2=\dfrac{25}{2}\pi \] So, the integral is \[ \int_2^{12} g(x)\,dx=40+\dfrac{25}{2}\pi \]

b. Fundamental Theorem of Calculus for Integrals

Use the FTC to find the area below \(y=x^3\) above the \(x\)-axis between \(x=1\) and \(x=3\).

\(\displaystyle A=\int_1^3 x^3\,dx=20\)

The area is \[\begin{aligned} A&=\int_1^3x^3\,dx=\left[\dfrac{x^4}{4}\right]_1^3\\ &=\left(\dfrac{3^4}{4}\right)-\left(\dfrac{1^4}{4}\right)=\dfrac{81}{4} -\dfrac{1}{4} =20 \end{aligned}\]

This integral was previously computed as a limit of Riemann sums. The FTC was so much easier!
Use the FTC to compute the integral \(\displaystyle \int_0^6 (3x^2-12x-5)\,dx\).

\(\displaystyle \int_0^6 3x^2-12x-5\,dx=-30\)

We find an antiderivative and evaluate it at the limits: \[\begin{aligned} \int_0^6 &3x^2-12x-5\,dx=\left[\rule{0pt}{10pt}x^3-6x^2-5x\right]_0^6\\ &=\left[6^3-6(6^2)-5(6)\right]-[0]=-30 \end{aligned}\]

rm,jr

This integral was previously computed as a limit of Riemann sums. The FTC was so much easier!
Use the FTC to compute the area below \(y=\dfrac{1}{x}\) above the \(x\)-axis between \(x=2\) and \(x=8\).

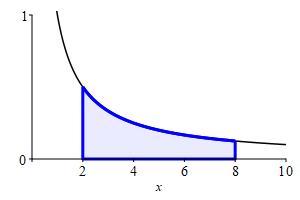
What is an antiderivative of \(\dfrac{1}{x}\)?

\(\displaystyle A=\int_2^8 \dfrac{1}{x}\,dx=2\ln 2\)

The area is \[\begin{aligned} A&=\int_2^8\dfrac{1}{x}\,dx=\left[\dfrac{}{}\ln x\right]_2^8\\ &=\left(\ln 8\right)-\left(\ln 2\right)=2\ln 2 \end{aligned}\]

This area was previously approximated using right Riemann sums to get \(R_3=\dfrac{13}{12}\approx1.08\). The FTC gives the exact area as \(A=2\ln 2\approx1.39\).
Use the FTC to compute the area below \(y=\sin\theta\) above the \(\theta\)-axis between \(\theta=0\) and \(\theta=\pi\).

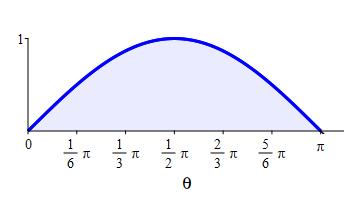
What is an antiderivative of \(\sin x\)? Is there a minus?

\(\displaystyle A=\int_0^\pi \sin x\, dx=2\)

The area is \[\begin{aligned} A&=\int_{0}^{\pi} \sin x\,dx =\left[\rule{0pt}{10pt}-\cos(x)\right]_0^\pi \\ &=-\cos(\pi)+\cos(0)=-(-1)+1=2 \end{aligned}\]

This area was previously approximated using right Riemann sums to get \(R_6=\dfrac{2+\sqrt{3}}{6}\pi \approx 1.95\). The FTC gives the exact area as \(A=2\).
Use the FTC to compute the integral \(\displaystyle \int_{-\pi/2}^{\pi} \cos\theta\,d\theta\).

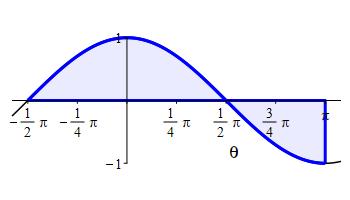
What is an antiderivative of \(\cos x\)? Is there a minus?

\(\displaystyle A=\int_{-\pi /2}^{\pi}\cos \theta =1\)

The area is \[\begin{aligned} A&=\int_{-\pi /2}^{\pi} \cos \theta\,d\theta =\left[\dfrac{}{}\sin(\theta)\right]_{-\pi /2}^{\pi} \\ &=\sin(\pi)-\sin(-\pi /2)=0+1=1 \end{aligned}\]

This area was previously approximated using right and left Riemann sums to get: \[ R_6=\dfrac{\sqrt{2} \pi}{8} \approx 0.56 \quad \text{and} \quad L_6=\dfrac{\pi}{4}\left(1+\dfrac{\sqrt{2}}{2}\right) \approx 1.34 \] The FTC gives the exact area as \(A=1\) which is right in the middle!

Use the \(2^\text{nd}\) Fundamental Theorem of Calculus to compute each of the following integrals.

\(\displaystyle \int_1^4 (4x^2-3x)\,dx\)

What is the antiderivative of \(4x^2-3x\)?

\(\displaystyle \int_1^4 (4x^2-3x)\,dx=\dfrac{123}{2}\)

An antiderivative of \(4x^2-3x\) is \(4\dfrac{x^3}{3}-3\dfrac{x^2}{2}\). So the FTC says: \[\begin{aligned} \int_1^4 &(4x^2-3x)\,dx =\left[4\dfrac{x^3}{3}-3\dfrac{x^2}{2}\right]_1^4 \\ &=4\dfrac{4^3}{3}-3\dfrac{4^2}{2}-4\dfrac{1^3}{3}+3\dfrac{1^2}{2} \\ &=4\dfrac{64-1}{3}-3\dfrac{16-1}{2} \\ &=4(21)-\dfrac{45}{2} =\dfrac{123}{2} \end{aligned}\]

jr
\(\displaystyle \int_1^4 4e^{3x}\,dx\)

What is the derivative of \(e^{3x}\)?

\(\displaystyle \int_1^4 4e^{3x}\,dx=\dfrac{4}{3}(e^{12}-e^3)\)

An antiderivative of \(4e^{3x}\) is \(\dfrac{4e^{3x}}{3}\). So the FTC says: \[\begin{aligned} \int_1^4 &4e^{3x}\,dx =\left[\dfrac{4e^{3x}}{3}\right]_1^4 \\ &=4\dfrac{e^{12}}{3}-4\dfrac{e^3}{3} \\ &=\dfrac{4}{3}(e^{12}-e^3) \end{aligned}\]

jr
\(\displaystyle \int_{-\pi /4}^{\pi /4} 4\sec^2x\,dx\)

What is the antiderivative of \(\sec^2x\)?

\(\displaystyle \int_{-\pi /4}^{\pi /4} 4\sec^2x\,dx = 8\)

An antiderivative of \(4\sec^2x\) is \(4\tan x\). So the FTC says: \[\begin{aligned} \int_{-\pi /4}^{\pi /4} &4\sec^2x\,dx =\left[\rule{0pt}{10pt}4\tan x\right]_{-\pi /4}^{\pi /4} \\ &=4\tan\left(\dfrac{\pi}{4}\right)-4\tan\left(-\dfrac{\pi}{4}\right) \\ &=4+4=8 \end{aligned}\]

jr
\(\displaystyle \int_{-1}^1 \dfrac{2}{1+x^2}\,dx\)

What is the antiderivative of \(\dfrac{1}{1+x^2}\)?

\(\displaystyle \int_{-1}^1 \dfrac{2}{1+x^2}\,dx = \pi\)

An antiderivative of \(\dfrac{2}{1+x^2}\) is \(2\arctan x\). So the FTC says: \[\begin{aligned} &\int_{-1}^1 \dfrac{2}{1+x^2}\,dx =\left[\rule{0pt}{10pt}2\arctan x\right]_{-1}^{1} \\ &=2\arctan\left(1\right)-2\arctan\left(-1\right) \\ &=2\dfrac{\pi}{4}-2\dfrac{-\pi}{4} =\pi \end{aligned}\]

jr
\(\displaystyle \int_{15}^{30} \dfrac{18}{x}\,dx\)

What is the antiderivative of \(\dfrac{1}{x}\)?

\(\displaystyle \int_{15}^{30} \dfrac{18}{x}\,dx = 18\ln{2}\)

An antiderivative of \(\dfrac{18}{x}\) is \(18\ln|x|\). So the FTC says: \[\begin{aligned} \int_{15}^{30} &\dfrac{18}{x}\,dx =\left[\rule{0pt}{10pt}18\ln|x|\right]_{15}^{30} \\ &=18\ln\left(30\right)-18\ln\left(15\right) \\ &=18\ln{2} \end{aligned}\]

jr
\(\displaystyle \int_0^\pi 2x\cos x-x^2\sin x\,dx\)

What is the antiderivative of \(2x\cos x-x^2\sin x\)? Think about the Product Rule.

\(\displaystyle \int_0^\pi 2x\cos x-x^2\sin x\,dx = -\pi^2\)

Since \(\dfrac{d}{dx}x^2=2x\) and \(\dfrac{d}{dx}\cos x=-\sin x\), this looks like the result of a Product Rule. So an antiderivative of \(2x\cos x-x^2\sin x\) is \(x^2\cos x\). Thus the FTC says: \[\begin{aligned} \int_0^\pi &2x\cos x-x^2\sin x\,dx =\left[\rule{0pt}{10pt}x^2\cos x\right]_{0}^{\pi} \\ &=\pi^2 \cos \pi-0 \cos 0 =-\pi^2 \end{aligned}\]

jr
\(\displaystyle \int_0^{\pi/3} 5\sec x\tan x\,dx\)

What is the antiderivative of \(\sec x\tan x\)?

\(\displaystyle \int_0^{\pi/3} 5\sec x\tan x\,dx = 5\)

An antiderivative of \(5\sec x\tan x\) is \(5\sec x\). So the FTC says: \[\begin{aligned} \int_0^{\pi/3} &5\sec x\tan x\,dx =\left[\rule{0pt}{10pt}5\sec x\right]_{0}^{\pi/3} \\ &=(5\sec\dfrac{\pi}{3})-5\left(\sec 0\right) \\ &= 10 - 5 = 5 \end{aligned}\]

jr
\(\displaystyle \int_{-1/2}^{\sqrt{3}/2} \dfrac{3}{\sqrt{1-x^2}}\,dx\)

What is the antiderivative of \(\dfrac{1}{\sqrt{1-x^2}}\)?

\(\displaystyle \int_{-1/2}^{\sqrt{3}/2} \dfrac{3}{\sqrt{1-x^2}}\,dx = \dfrac{3\pi}{2}\)

An antiderivative of \(\dfrac{3}{\sqrt{1-x^2}}\) is \(3\arcsin x\). So the FTC says: \[\begin{aligned} &\int_{-1/2}^{\sqrt{3}/2} \dfrac{3}{\sqrt{1-x^2}}\,dx =\left[\rule{0pt}{10pt}3\arcsin x\right]_{-1/2}^{\sqrt{3}/2} \\ &=(3\arcsin\dfrac{\sqrt3}{2})-3\left(\arcsin\dfrac{-1}{2}\right) \\ &=3\left(\dfrac{\pi}{3}\right) - 3\left(\dfrac{-\pi}{6}\right) =\dfrac{3\pi}{2} \end{aligned}\]

jr
\(\displaystyle \int_{\pi / 4}^{3\pi / 4} \dfrac{4\sin x - 4x\cos x}{\sin^2x}\,dx\)

What is the antiderivative of \(\dfrac{4\sin x - 4x\cos x}{\sin^2x}\)? Think about the Quotient Rule.

\(\displaystyle \int_{\pi / 4}^{3\pi / 4} \dfrac{4\sin x - 4x\cos x}{\sin^2x}\,dx = 2\sqrt 2 \pi\)

Since \(\dfrac{d}{dx}(4x)=4\) and \(\dfrac{d}{dx}\sin x=\cos x\) and \(\sin^2x\) appears in the denominator, this looks like the result of a Quotient Rule. So an antiderivative of \(\dfrac{4\sin x - 4x\cos x}{\sin^2x}\) is \(\dfrac{4x}{\sin x}\). Thus the FTC says: \[\begin{aligned} \int_{\pi/4}^{3\pi/4} &\dfrac{4\sin x-4x\cos x}{\sin^2x}\,dx =\left[\dfrac{4x}{\sin x}\right]_{\pi/4}^{3\pi/4} \\ &=\left(\dfrac{3\pi}{\sin\dfrac{3\pi}{4}}\right)-\left(\dfrac{\pi}{\sin\dfrac{\pi}{4}}\right) \\ &=3\sqrt{2}\pi-\sqrt{2}\pi =2\sqrt 2\pi \end{aligned}\] since \(\sin\dfrac{\pi}{4}=\sin\dfrac{3\pi}{4}=\dfrac{1}{\sqrt{2}}\).

jr
\(\displaystyle \int_{1}^{7} 3x^2-\dfrac{2}{x}\,dx\)

What is the antiderivative of \(3x^2-\dfrac{2}{x}\)?

\(\displaystyle \int_{1}^{7} 3x^2-\dfrac{2}{x}\,dx = 342 - 2\ln7\)

An antiderivative of \(3x^2-\dfrac{2}{x}\) is \(x^3-2\ln|x|\). So the FTC says: \[\begin{aligned} \int_{1}^{7} &3x^2-\dfrac{2}{x}\,dx =\left[\rule{0pt}{10pt}x^3-2\ln|x|\right]_{1}^{7} \\ &=(7^3-2\ln7)-(1^3-2\ln 1) \\ &= 343 - 2\ln7 -1 = 342 - 2\ln7 \end{aligned}\]

jr

Use the \(1^\text{st}\) Fundamental Theorem of Calculus or Leibniz's Method to compute each of the following derivatives.

Compute \(\displaystyle \dfrac{d}{dx}\int_2^x \dfrac{2}{1+t^4}\,dt\).

Use the \(1^\text{st}\) Fundamental Theorem of Calculus.

\(\displaystyle \dfrac{d}{dx}\int_2^x \dfrac{2}{1+t^4}\,dt=\dfrac{2}{1+x^4}\)

By the \(1^\text{st}\) Fundamental Theorem of Calculus, the derivative of an integral with respect to its upper limit is just the integrand with the variable changed to the upper limit: \[ \dfrac{d}{dx}\int_2^x \dfrac{2}{1+t^4}\,dt=\dfrac{2}{1+x^4} \]

rn,dc
Compute \(\displaystyle \dfrac{d}{dy}\int_2^y e^{p^2}\,dp\).

\(\displaystyle \dfrac{d}{dy}\int_2^y e^{p^2}\,dp=e^{y^2}\)

By the \(1^\text{st}\) Fundamental Theorem of Calculus, the derivative of an integral with respect to its upper limit is just the integrand with the variable changed to the upper limit: \[ \dfrac{d}{dy}\int_2^y e^{p^2}\,dp=e^{y^2} \]

rn,dc
Compute \(\displaystyle \dfrac{d}{dx}\int_x^3 \dfrac{2}{1+t^4}\,dt\).

Let \(F(t)\) be an antiderivative of \(\dfrac{2}{1+t^4}\) and use the \(2^\text{nd}\) Fundamental Theorem of Calculus before differentiating.

\(\displaystyle \dfrac{d}{dx}\int_x^3 \dfrac{2}{1+t^4}\,dt=-\,\dfrac{2}{1+x^4}\)

In order to use the \(2^\text{nd}\) Fundamental Theorem of Calculus, we let \(F(t)\) be any antiderivative of the integrand \(\dfrac{2}{1+t^4}\). In other words: \[ F'(t)=\dfrac{2}{1+t^4} \qquad \qquad (*) \] Then by the \(2^\text{nd}\) Fundamental Theorem of Calculus: \[ \int_x^3 \dfrac{2}{1+t^4}\,dt=F(3)-F(x) \] We can now differentiate this, but first notice that \(F(3)\) is a constant. So: \[\begin{aligned} \dfrac{d}{dx}&\int_x^3 \dfrac{2}{1+t^4}\,dt =\dfrac{d}{dx}(F(3)-F(x)) \\ &=-F'(x)=-\,\dfrac{2}{1+x^4} \end{aligned}\] where in the last step we have used equation (*) with \(t\) replaced by \(x\). Thus, the derivative of an integral with respect to its lower limit is just the negative of the integrand with the variable changed to the lower limit.

rn,dc
Compute \(\displaystyle \dfrac{d}{dy}\int_y^3 e^{p^2}\,dp\).

\(\displaystyle \dfrac{d}{dy}\int_y^3 e^{p^2}\,dp=-e^{y^2}\)

In order to use the \(2^\text{nd}\) Fundamental Theorem of Calculus, we let \(F(p)\) be any antiderivative of the integrand \(e^{p^2}\). In other words: \[ F'(p)=e^{p^2} \qquad \qquad (*) \] Then by the \(2^\text{nd}\) Fundamental Theorem of Calculus: \[ \int_y^3 e^{p^2}\,dp=F(3)-F(y) \] We can now differentiate this, but first notice that \(F(3)\) is a constant. So: \[\begin{aligned} \dfrac{d}{dy}&\int_y^3 e^{p^2}\,dp =\dfrac{d}{dy}(F(3)-F(y)) \\ &=-F'(y)=-e^{y^2} \end{aligned}\] where in the last step we have used equation (*) with \(p\) replaced by \(y\).

rn,dc
Compute \(\displaystyle \dfrac{d}{dx}\int_{2x}^{x^2} \dfrac{2}{1+t^4}\,dt\).

Let \(F(t)\) be an antiderivative of \(\dfrac{2}{1+t^4}\) and use the \(2^\text{nd}\) Fundamental Theorem of Calculus followed by the Chain Rule.

\(\displaystyle \dfrac{d}{dx}\int_{2x}^{x^2} \dfrac{2}{1+t^4}\,dt=\dfrac{4x}{1+x^8}-\dfrac{4}{1+16x^4}\)

Here's where we really use Leibniz's Method: We again let \(F(t)\) be any antiderivative of the integrand \(\dfrac{2}{1+t^4}\). So: \[ F'(t)=\dfrac{2}{1+t^4} \qquad \qquad (1) \] Then by the \(2^\text{nd}\) Fundamental Theorem of Calculus: \[ \int_{2x}^{x^2} \dfrac{2}{1+t^4}\,dt=F(x^2)-F(2x) \] We can now differentiate this, but we need to use the Chain Rule: \[\begin{aligned} \dfrac{d}{dx}&\int_{2x}^{x^2} \dfrac{2}{1+t^4}\,dt =\dfrac{d}{dx}\left[F(x^2)-F(2x)\right] \\ &=F'(x^2)\dfrac{d}{dx}[x^2]-F'(2x)\dfrac{d}{dx}[2x] \qquad \qquad (2) \\ &=\dfrac{2}{1+x^8}(2x)-\dfrac{2}{1+16x^4}(2) \qquad \qquad (3) \\ &=\dfrac{4x}{1+x^8}-\dfrac{4}{1+16x^4} \end{aligned}\] where in step (2) we have used the Chain Rule which says the derivative of a composition is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. Then in step (3) we have used equation (1) with \(t\) replaced first by \(x^2\) and then by \(2x\).

rn,dc
Compute \(\displaystyle \dfrac{d}{dy}\int_{y^2}^{3y} e^{p^2}\,dp\).

\(\displaystyle \dfrac{d}{dy}\int_{y^2}^{3y} e^{p^2}\,dp=3e^{9y^2}-2ye^{y^4}\)

We again use Leibniz's Method: We let \(F(t)\) be any antiderivative of the integrand \(e^{p^2}\). So: \[ F'(p)=e^{p^2} \qquad \qquad (1) \] Then by the \(2^\text{nd}\) Fundamental Theorem of Calculus: \[ \int_{y^2}^{3y} e^{p^2}\,dp=F(3y)-F(y^2) \] We can now differentiate this, but we need to use the Chain Rule: \[\begin{aligned} \dfrac{d}{dy}&\int_{y^2}^{3y} e^{p^2}\,dp =\dfrac{d}{dy}\left[F(3y)-F(y^2)\right] \\ &=F'(3y)\dfrac{d}{dy}[3y]-F'(y^2)\dfrac{d}{dy}[y^2] \qquad \qquad (2) \\ &=e^{9y^2}(3)-e^{y^4}(2y) \qquad \qquad (3) \\ &=3e^{9y^2}-2ye^{y^4} \end{aligned}\] where in step (2) we have used the Chain Rule which says the derivative of a composition is the derivative of the outer function evaluated at the inner function times the derivative of the inner function. Then in step (3) we have used equation (1) with \(p\) replaced first by \(3y\) and then by \(y^2\).

rn,dc

c. Indefinite Integrals

Compute each of the following indefinite integrals.

\(\displaystyle \int 3x^5\,dx\)

\(\displaystyle \int 3x^5\,dx=\dfrac{x^6}{2}+C \)

The derivative of \(x^6\) is \(6x^5\). So: \[ \int 3x^5\,dx=\dfrac{x^6}{2}+C \]
\(\displaystyle \int 6x^2 e^{x^3}\,dx\)

\(\displaystyle \int 6x^2 e^{x^3}\,dx=2e^{x^3}+C\)

By the Chain Rule, we know \(\dfrac{d}{dx}e^{x^3}=e^{x^3}3x^2\). So \(\dfrac{d}{dx}(2e^{x^3})=6x^2e^{x^3}\) and: \[ \int 6x^2 e^{x^3}\,dx=2e^{x^3}+C \]
\(\displaystyle \int \dfrac{10}{2x-3}\,dx\)

The antiderivative of \(\dfrac{1}{x}\) is \(\ln|x|\).

\(\displaystyle \int \dfrac{10}{2x-3}\,dx=5\ln|2x-3|+C\)

Since \(\dfrac{d}{dx}\ln|x|=\dfrac{1}{x}\), we try \(\dfrac{d}{dx}\ln|2x-3|=\dfrac{1}{2x-3}\cdot2\). (Here we used the Chain Rule.) We are off by a \(5\). So: \[ \int \dfrac{10}{2x-3}\,dx=5\ln|2x-3|+C \]
\(\displaystyle \int \csc^2x\,dx\)

\(\displaystyle \int \csc^2x\,dx=-\cot x+C\)

The derivative of \(\cot x\) is \(-\csc^2x\). So \[ \int \csc^2x\,dx=-\cot x+C \]
\(\displaystyle \int \dfrac{1}{1+x^2}\,dx\)

Which inverse trig function has derivative \(\dfrac{1}{1+x^2}\)?

\(\displaystyle \int \dfrac{1}{1+x^2}\,dx=\arctan x+C\)

The derivative of \(\arctan x\) is \(\dfrac{1}{1+x^2}\). So \[ \int \dfrac{1}{1+x^2}\,dx=\arctan x+C \]

bl
\(\displaystyle \int \cosh t\,dt\) See the page on integrals of hyperbolic trig functions.

\(\dfrac{d}{dt}\sinh t=\cosh t\)

\(\displaystyle \int \cosh t\,dt=\sinh t+C\)

The derivative of \(\sinh t\) is \(\cosh t\). So \(\displaystyle \int\cosh t\,dt=\sinh t+C\).

d. Integration Rules and Properties

Which is larger, \(\displaystyle \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \cos(x^2)\, dx\) or \(\displaystyle \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \sec(x^2)\, dx\), and why?

\(\displaystyle \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \sec(x^2)\, dx\) is larger because \(\cos(x^2) \le 1 \le \sec(x^2)\) on this interval.

The graphs of \(\cos(x^2)\) in blue and \(\sec(x^2)\) in red show that \(\cos(x^2)\) is always smaller than \(1\) while \(\sec(x^2)\) is always larger than \(1\). So: \[ \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \sec(x^2)\, dx \gt \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \cos(x^2)\, dx \]
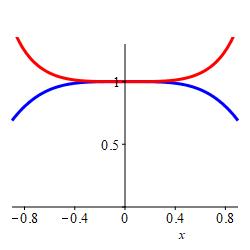
Find upper and lower bounds for \(\displaystyle \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \cos(x^2)\, dx\) using the minimum and maximum values of \(\cos(x^2)\) on the interval \(\left[-\sqrt{\dfrac{\pi}{4}},\sqrt{\dfrac{\pi}{4}}\right]\).

\[ \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} m\, dx \le \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \cos(x^2)\, dx \le \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} M\, dx \] where \(m\) and \(M\) are the minimum and maximum of \(\cos(x^2)\) on the interval.

Upper bound: \(\sqrt{\pi}\), Lower bound: \(\sqrt{\dfrac{\pi}{2}}\)

\(\cos\left(x^2\right)\) is largest at \(x=0\) with the value of \(1\) and smallest at \(x=\pm\sqrt{\dfrac{\pi}{4}}\) with the value of \(\dfrac{\sqrt2}{2}\). So: \[ \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \dfrac{\sqrt2}{2}\, dx \le \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \cos(x^2)\, dx \le \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} 1\, dx \] Therefore: \[ \dfrac{\sqrt2}{2}\cdot2\sqrt{\dfrac{\pi}{4}} \le \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \cos(x^2)\, dx \le 1\cdot2\sqrt{\dfrac{\pi}{4}} \] or: \[ \sqrt{\dfrac{\pi}{2}} \le \int_{-\sqrt{\pi/4}}^{\sqrt{\pi/4}} \cos(x^2)\, dx \le \sqrt{\pi} \]
Find the area below \(y=|x-2|+3\) above the \(x\)-axis between \(x=0\) and \(x=3\).

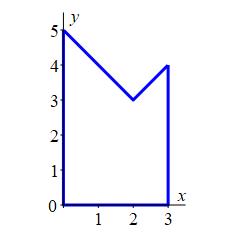
Split the integral at \(x=2\).

\(\displaystyle A=\dfrac{23}{2}\)

We split the bounds into \(0\) to \(2\) where \(|x-2|=2-x\) and \(\ 2\) to \(\ 3\) where \(|x-2|=x-2\). Then the area is the integral: \[\begin{aligned} A&=\int_0^3 (|x-2|+3)\,dx =\int_0^2 (2-x+3)\,dx + \int_2^3 (x-2+3)\,dx \\ &=\left[5x-\dfrac{x^2}{2}\right]_0^2+\left[\dfrac{x^2}{2}+x\right]_2^3 =8+ \dfrac{7}{2} =\dfrac{23}{2} \end{aligned}\]

The integral can also be done by looking at the graph and adding the areas of a square of side \(3\) and two triangles one of width and height \(2\) and the other of width and height \(1\): \[ A=3^2+\dfrac{1}{2}2^2+\dfrac{1}{2}1^2=\dfrac{23}{2} \]
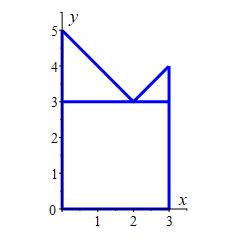
Find the area below \(y=|x^2-5x+6|\) above the \(x\)-axis between \(x=0\) and \(x=5\).

When is \(x^2-5x+6\) positive or negative?

\(\displaystyle A=\dfrac{19}{2}\)

The area is \[ A=\int_0^5 |x^2-5x+6|\, dx \] We factor the quantity inside the absolute value: \[ x^2-5x+6=(x-2)(x-3) \] This is positive when \(x \gt 3\) or \(x \lt 2\) and negative when \(2 \lt x \lt 3\). So we split the bounds at \(2\) and \(3\).

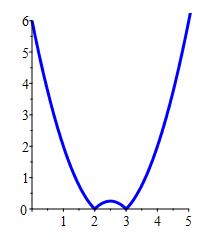
On \([0,2]\), we have \(|x^2-5x+6|=x^2-5x+6\).
On \([2,3]\), we have \(|x^2-5x+6|=-x^2+5x-6\).
On \([3,5]\), we have \(|x^2-5x+6|=x^2-5x+6\).
Therefore, the area is the integral: \[\begin{aligned} A&=\int_0^5 |x^2-5x+6|\,dx \\ &=\int_0^2 (x^2-5x+6)\,dx + \int_2^3 (-x^2+5x-6)\,dx + \int_3^5 (x^2-5x+6)\,dx \\ &=\left[\dfrac{x^3}{3}-\dfrac{5x^2}{2}+6x\right]_0^2 +\left[-\dfrac{x^3}{3}+\dfrac{5x^2}{2}-6x\right]_2^3 +\left[\dfrac{x^3}{3}-\dfrac{5x^2}{2}+6x\right]_3^5 \\ &=\dfrac{14}{3}+\dfrac{1}{6}+\dfrac{14}{3} =\dfrac{19}{2} \end{aligned}\]