22. Riemann Sums, Integrals and the FTC

b. The Fundamental Theorem of Calculus for Integrals

1. The \(1^\text{st}\) and \(2^\text{nd}\) Fundamental Theorems

We need to generalize from the Fundamental Theorem of Calculus for Area (which applies to integrals with a positive integrand) to that for general integrals (with integrands which are not necessarily positive).

Given a function \(f(x)\) defined on an interval \([a,b]\) which is not necessarily positive, the integral, \[I(a,b)=\int_a^b f(x)\,dx\] gives the net area, i.e. the difference between the area under the curve above the \(x\)-axis (shown in light magenta) and the area above the curve below the \(x\)-axis (shown in dark magenta). If we fix the left endpoint, \(a\), and let the right endpoint be a variable, \(x\), we get the Integral Function for \(f(x)\) starting at \(x=a\): \[I_a(x)=\int_a^x f(t)\,dt\] Notice that we change the variable of integration from \(x\) to \(t\) to prevent confusion between the right endpoint \(x\) and the variable \(t\) which can be any value between \(a\) and \(x\).

We can now compute the derivative of the integral function, \(I_a(x)\), just as we did for the area function, \(A_a(x)\), in the previous chapter.

If \(I_a(x)\) is the integral function for \(f(x)\) starting at \(x=a\), then its derivative is \(f(x)\). That is: \[ \dfrac{d}{dx}I_a(x)=f(x) \] The proof is nearly identical to the one for the area function.

Throughout the proof, we will write \(I(x)\) instead of \(I_a(x)\).

We wish to find the derivative of the integral function, \(I(x)\), shown in magenta. Light magenta makes a positive contribution. Dark magenta makes a negative contribution.

By definition, the derivative is \[ I^\prime(x)=\lim_{h\to0}\dfrac{I(x+h)-I(x)}{h} \] Notice that in this limit, \(x\) is a constant and \(h\) is the variable. We examine the quotient.

We first look at the case when \(x\) happens to be a point where \(f(x) \ge 0\) as shown here. We will come back to the case when \(f(x) \lt 0\) later.

In this plot, \(I(x)\) is shown in magenta, while \(I(x+h)\) is shown in magenta and green together. Light color is positive while dark color is negative. So the numerator is the difference, \(I(x+h)-I(x)\), which is shown in green alone. Consequently, the quotient is the green area divided by \(h\) and we need to take the limit as \(h\) goes to zero.

To compute the limit, we approximate the net green) area, \(I(x+h)-I(x)\), by the blue (and light green) rectangle. When \(h\) is small, there is a positive rectangle whose height is \(f(x)\) and whose width is \(h\). So the numerator is approximately: \[ I(x+h)-I(x)\approx f(x)\cdot h \] (This approximation gets better as \(h\) approaches \(0\).) So the quotient is approximately: \[ \dfrac{I(x+h)-I(x)}{h}\approx f(x) \] Notice that this value is independent of \(h\). So the limit is: \[ I'(x) =\lim_{h\to0}\dfrac{I(x+h)-I(x)}{h} =\lim_{h\to0}f(x)=f(x) \]

We now look at the case when \(x\) is a point where \(f(x) \lt 0\) as shown.

We approximate the green net area, \(I(x+h)-I(x)\), by the blue rectangle. When \(h\) is small, there is a negative rectangle whose height is \(|f(x)|\) and whose width is \(h\). So the numerator is approximately: \[ I(x+h)-I(x)\approx f(x)\cdot h \] which is negative because \(f(x)\) is negative. So the quotient is approximately: \[ \dfrac{I(x+h)-I(x)}{h}\approx f(x) \] Since this value is independent of \(h\), the limit is: \[ I'(x) =\lim_{h\to0}\dfrac{I(x+h)-I(x)}{h} =\lim_{h\to0}f(x)=f(x) \]

In both cases, we conclude the derivative of the integral function is the original function: \[ I'(x)=f(x) \]

We conclude that \(\displaystyle I_a(x)=\int_a^x f(t)\,dt\) is an antiderivative of \(f(x)\). This is the first version of the Fundamental Theorem of Calculus:

Given a function \(f(x)\) defined on an interval \([a,b]\), then its integral function is an antiderivative of the original function, \(f(x)\): \[ \dfrac{d}{dx}\int_a^x f(t)\,dt=f(x) \]

The theorem says, "The derivative of an integral with respect to its upper limit is the integrand with its variable replaced by the upper limit." Notice that it is even more important now to distinguish between the variable of integration, \(t\), and the upper limit, \(x\).

Notice that \(\displaystyle I_a(a)=\int_a^a f(t)\,dt=0\) since this is the net area between \(f(x)\) and the \(x\)-axis between \(x=a\) and \(x=a\) which is obviously zero. Consequently, the differential equation together with the initial condition \[ \dfrac{d}{dx}I_a(x)=f(x) \qquad \text{with} \qquad I_a(a)=0 \] is an initial value problem to be solved for \(I_a(x)\).

Solve the initial value problem: \[ \dfrac{d}{dx}I_a(x)=f(x) \qquad \text{with} \qquad I_a(a)=0 \]

Let \(F(x)\) be an arbitrary antiderivative of \(f(x)\). Then \[ I_a(x)=F(x)+C \] The initial condition says \[ I_a(a)=F(a)+C=0 \qquad \Longrightarrow \qquad C=-F(a) \] So \[ I_a(x)=F(x)-F(a) \] Setting \(x=b\), we have \[ I_a(b)=F(b)-F(a) \] which is the second version of the Fundamental Theorem of Calculus:

Given a function \(f(x)\) defined on an interval \([a,b]\), then: \[ \int_a^b f(x)\,dx=\left.F(x)\rule{0pt}{10pt}\right|_a^b=F(b)-F(a) \] where \(F(x)\) is any antiderivative of \(f(x)\).

The following are the same example and exercise as on the previous page except solved using the FTC instead of limits of Riemann sums.

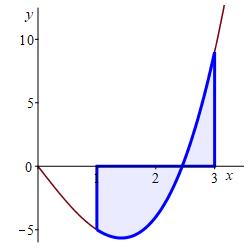
Compute the integral \(\displaystyle \int_1^3 x^3-6x\,dx\) using the FTC.

We find an antiderivative and evaluate it at the limits: \[\begin{aligned} \int_1^3 &x^3-6x\,dx =\left[\dfrac{x^4}{4}-3x^2\right]_1^3 \\ &=\dfrac{3^4}{4}-3^3-\dfrac{1}{4}+3=-4 \end{aligned}\] That was so much quicker than the Riemann sums!

Compute the integral \(\displaystyle \int_1^9(x^2+1)\,dx\) using the FTC.

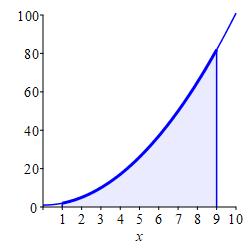
\(\displaystyle \int_1^9(x^2+1)\,dx=\dfrac{752}{3}\)

We find an antiderivative and evaluate it at the limits: \[\begin{aligned} \int_1^9 &(x^2+1)\,dx =\left[\dfrac{x^3}{3}+x\right]_1^9 \\ &=\left(\dfrac{9^3}{3}+9\right)-(\dfrac{1}{3}+1) =\dfrac{728}{3}+8=\dfrac{752}{3} \end{aligned}\] Again, that was so much easier than the Riemann sums!

22. Riemann Sums, Integrals and the FTC

b. The Fundamental Theorem of Calculus for Integrals

1. The \(1^\text{st}\) and \(2^\text{nd}\) Fundamental Theorems

Heading