1. Trigonometry

Exercises

a. Angular Measure

What is \(\dfrac{2}{3}\) of a circle in terms of radians?

One full circle is \(2\pi\) radians. So to express a fraction of a circle in terms of radians, we multiply it by \(2\pi\).

\(\dfrac{2}{3}\) of a circle is \(\dfrac{4\pi}{3}\,\text{rad}\).

One full circle is \(2\pi\) radians. So \(\dfrac{2}{3}\) of a circle is: \[ \dfrac{2}{3}\cdot2\pi\, \text{rad}=\dfrac{4\pi}{3}\text{rad} \]

aas
What is \(\dfrac{1}{6}\) of a circle in terms of radians?

One full circle is \(2\pi\) radians. So to express a fraction of a circle in terms of radians, we multiply the fraction by \(2\pi\).

\(\dfrac{1}{6}\) of a circle is \(\dfrac{\pi}{3}\,\text{rad}\).

One full circle is \(2\pi\) radians. So \(\dfrac{1}{6}\) of a circle is: \[ \dfrac{1}{6}\cdot2\pi\, \text{rad}=\dfrac{\pi}{3}\text{rad} \]

aas
What is \(270^\circ\) in terms of radians?

A half circle is either \(180^\circ\) or \(\pi\) radians. So to convert an angle, we multiply it by \(1\) in the form \(\dfrac{\pi\,\text{rad}}{180^\circ}\) or \(\dfrac{180^\circ}{\pi\,\text{rad}}\) and be sure that units cancel.

\(270^\circ=\dfrac{3\pi}{2}\,\text{rad}\)

A half circle is either \(180^\circ\) or \(\pi\) radians. So to convert an angle, we multiply it by \(1\) in the form \(\dfrac{\pi\,\text{rad}}{180^\circ}\) or \(\dfrac{180^\circ}{\pi\,\text{rad}}\) and be sure that units cancel. Here we convert \(270^\circ\). Notice that the degrees cancel between the numerator and the denominator: \[ 270^\circ=270^\circ\dfrac{\pi\,\text{rad}}{180^\circ} =\dfrac{3\pi}{2}\,\text{rad} \]

aas
What is \(300^\circ\) in terms of radians?

A half circle is either \(180^\circ\) or \(\pi\) radians. So to convert an angle, we multiply it by \(1\) in the form \(\dfrac{\pi\,\text{rad}}{180^\circ}\) or \(\dfrac{180^\circ}{\pi\,\text{rad}}\) and be sure that units cancel.

\(300^\circ=\dfrac{5\pi}{3}\,\text{rad}\)

A half circle is either \(180^\circ\) or \(\pi\) radians. So to convert an angle, we multiply it by \(1\) in the form \(\dfrac{\pi\,\text{rad}}{180^\circ}\) or \(\dfrac{180^\circ}{\pi\,\text{rad}}\) and be sure that units cancel. Here we convert \(300^\circ\). Notice that the degrees cancel between the numerator and the denominator: \[ 300^\circ=300^\circ\dfrac{\pi\,\text{rad}}{180^\circ} =\dfrac{5\pi}{3}\,\text{rad} \]

aas
What is \(\dfrac{\pi}{12}\) radians in terms of degrees?

A half circle is either \(180^\circ\) or \(\pi\) radians. So to convert an angle, we multiply it by \(1\) in the form \(\dfrac{\pi\,\text{rad}}{180^\circ}\) or \(\dfrac{180^\circ}{\pi\,\text{rad}}\) and be sure that units cancel.

\(\dfrac{\pi}{12}\,\text{rad}=15^\circ\)

A half circle is either \(180^\circ\) or \(\pi\) radians. So to convert an angle, we multiply it by \(1\) in the form \(\dfrac{\pi\,\text{rad}}{180^\circ}\) or \(\dfrac{180^\circ}{\pi\,\text{rad}}\) and be sure that units cancel. Here we convert \(\dfrac{\pi}{12}\) radians to degrees. Notice that the radians cancel between the numerator and the denominator: \[ \dfrac{\pi}{12}\,\text{rad}=\dfrac{\pi}{12}\,\text{rad}\cdot\dfrac{180^\circ} {\pi\,\text{rad}}=\dfrac{180^\circ}{12}=15^\circ \]

aas
What is \(\dfrac{7\pi}{6}\) radians in terms of degrees?

A half circle is either \(180^\circ\) or \(\pi\) radians. So to convert an angle, we multiply it by \(1\) in the form \(\dfrac{\pi\,\text{rad}}{180^\circ}\) or \(\dfrac{180^\circ}{\pi\,\text{rad}}\) and be sure that units cancel.

\(\dfrac{7\pi}{6}\,\text{rad}=210^\circ\)

A half circle is either \(180^\circ\) or \(\pi\) radians. So to convert an angle, we multiply it by \(1\) in the form \(\dfrac{\pi\,\text{rad}}{180^\circ}\) or \(\dfrac{180^\circ}{\pi\,\text{rad}}\) and be sure that units cancel. Here we convert \(\dfrac{7\pi}{6}\) radians and cancel the radians: \[ \dfrac{7\pi}{6}\,\text{rad}=\dfrac{7\pi}{6}\,\text{rad}\cdot\dfrac{180^\circ} {\pi\,\text{rad}}=7\cdot\dfrac{180^\circ}{6}=7\cdot30^\circ=210^\circ \]

aas

b. Triangle Definitions

An angle, \(\alpha\), in a right triangle has opposite and adjacent sides of lengths \(a=5\) and \(b=12\), respectively. Find the six trig functions for \(\alpha\).

Remember SOH CAH TOA: \[\begin{aligned} \sin\alpha&=\dfrac{\text{opp}}{\text{hyp}} \qquad \cos\alpha=\dfrac{\text{adj}}{\text{hyp}} \\ \tan\alpha&=\dfrac{\text{opp}}{\text{adj}} \qquad \cot\alpha=\dfrac{\text{adj}}{\text{opp}} \\ \sec\alpha&=\dfrac{\text{hyp}}{\text{adj}} \qquad \csc\alpha=\dfrac{\text{hyp}}{\text{opp}} \end{aligned}\] Use Pythagorean Theorem, \(c^2=a^2+b^2\), to calculate the length of the hypotenuse.

\(\begin{aligned} \sin\alpha=\dfrac{5}{13} &\qquad \cos\alpha=\dfrac{12}{13} \\ \tan\alpha=\dfrac{5}{12} &\qquad \cot\alpha=\dfrac{12}{5} \\ \sec\alpha=\dfrac{13}{12} &\qquad \csc\alpha=\dfrac{13}{5} \end{aligned}\)

The length of the hypotenuse may be calculated as: \[ c=\sqrt{a^2+b^2}=\sqrt{5^2+12^2}=\sqrt{169}=13 \] Then \(\text{opp}=a=5\), \(\text{adj}=b=12\), and \(\text{hyp}=c=13\). So: \[\begin{aligned} \sin\alpha&=\dfrac{\text{opp}}{\text{hyp}}=\dfrac{5}{13} \\ \cos\alpha&=\dfrac{\text{adj}}{\text{hyp}}=\dfrac{12}{13} \\ \tan\alpha&=\dfrac{\text{opp}}{\text{adj}}=\dfrac{5}{12} \\ \cot\alpha&=\dfrac{\text{adj}}{\text{opp}}=\dfrac{12}{5} \\ \sec\alpha&=\dfrac{\text{hyp}}{\text{adj}}=\dfrac{13}{12} \\ \csc\alpha&=\dfrac{\text{hyp}}{\text{opp}}=\dfrac{13}{5} \end{aligned}\]

aas
An angle, \(\beta\), in a right triangle has opposite and adjacent sides of lengths \(a=7\) and \(b=24\), respectively. Find the six trig functions for \(\beta\).

Remember SOH CAH TOA: \[\begin{aligned} \sin\beta&=\dfrac{\text{opp}}{\text{hyp}} \qquad \cos\beta=\dfrac{\text{adj}}{\text{hyp}} \\ \tan\beta&=\dfrac{\text{opp}}{\text{adj}} \qquad \cot\beta=\dfrac{\text{adj}}{\text{opp}} \\ \sec\beta&=\dfrac{\text{hyp}}{\text{adj}} \qquad \csc\beta=\dfrac{\text{hyp}}{\text{opp}} \end{aligned}\] Use Pythagorean Theorem, \(c^2=a^2+b^2\), to calculate the length of the hypotenuse.

\(\begin{aligned} \sin\beta=\dfrac{7}{25} &\qquad \cos\beta=\dfrac{24}{25} \\ \tan\beta=\dfrac{7}{24} &\qquad \cot\beta=\dfrac{24}{7} \\ \sec\beta=\dfrac{25}{24} &\qquad \csc\beta=\dfrac{25}{7} \end{aligned}\)

The length of the hypotenuse is calculated as such: \[ c=\sqrt{a^{2}+b^{2}}=\sqrt{7^2+24^2}=\sqrt{49+576}=\sqrt{625}=25 \] Then \(\text{opp}=a=7\), \(\text{adj}=b=24\), and \(\text{hyp}=c=25\). So: \[\begin{aligned} \sin\beta&=\dfrac{\text{opp}}{\text{hyp}}=\dfrac{7}{25} \\ \cos\beta&=\dfrac{\text{adj}}{\text{hyp}}=\dfrac{24}{25} \\ \tan\beta&=\dfrac{\text{opp}}{\text{adj}}=\dfrac{7}{24} \\ \cot\beta&=\dfrac{\text{adj}}{\text{opp}}=\dfrac{24}{7} \\ \sec\beta&=\dfrac{\text{hyp}}{\text{adj}}=\dfrac{25}{24} \\ \csc\beta&=\dfrac{\text{hyp}}{\text{opp}}=\dfrac{25}{7} \end{aligned}\]

aas
An angle, \(\alpha\), in a right triangle has hypotenuse and adjacent side of lengths \(c=1\) and \(b=.6\), respectively. Find the six trig functions for \(\alpha\).

Remember SOH CAH TOA: \[\begin{aligned} \sin\alpha&=\dfrac{\text{opp}}{\text{hyp}} \qquad \cos\alpha=\dfrac{\text{adj}}{\text{hyp}} \\ \tan\alpha&=\dfrac{\text{opp}}{\text{adj}} \qquad \cot\alpha=\dfrac{\text{adj}}{\text{opp}} \\ \sec\alpha&=\dfrac{\text{hyp}}{\text{adj}} \qquad \csc\alpha=\dfrac{\text{hyp}}{\text{opp}} \end{aligned}\] First calculate the length of the opposite side using the Pythagorean Theorem, \(c^2=a^2+b^2\).

\(\begin{aligned} \sin\alpha=\dfrac{4}{5} &\qquad \cos\alpha=\dfrac{3}{5} \\ \tan\alpha=\dfrac{4}{3} &\qquad \cot\alpha=\dfrac{3}{4} \\ \sec\alpha=\dfrac{5}{3} &\qquad \csc\alpha=\dfrac{5}{4} \end{aligned}\)

The length of the opposite side is calculated as such: \[\begin{aligned} a^{2}&=c^{2}-b^{2} \\ a&=\sqrt{c^{2}-b^{2}} \\ a&=\sqrt{1^{2}-.6^{2}}=\sqrt{1-.36} \\ &=\sqrt{.64}=.8 \end{aligned}\] So, the opposite side has a length \(.8\), the adjacent side a length \(.6\), and the hypotenuse a length \(1\). Then: \[\begin{aligned} \sin\alpha&=\dfrac{\text{opp}}{\text{hyp}}=\dfrac{.8}{1}=\dfrac{8}{10}=\dfrac{4}{5} \\ \cos\alpha&=\dfrac{\text{adj}}{\text{hyp}}=\dfrac{.6}{1}=\dfrac{6}{10}=\dfrac{3}{5} \\ \tan\alpha&=\dfrac{\text{opp}}{\text{adj}}=\dfrac{.8}{.6}=\dfrac{8}{6}=\dfrac{4}{3} \\ \cot\alpha&=\dfrac{\text{adj}}{\text{opp}}=\dfrac{.6}{.8}=\dfrac{6}{8}=\dfrac{3}{4} \\ \sec\alpha&=\dfrac{\text{hyp}}{\text{adj}}=\dfrac{1}{.6}=\dfrac{1}{\;\dfrac{6}{10}\;} =\dfrac{5}{3} \\ \csc\alpha&=\dfrac{\text{hyp}}{\text{opp}}=\dfrac{1}{.8}=\dfrac{1}{\;\dfrac{4}{5}\;} =\dfrac{5}{4} \end{aligned}\]

aas

Notice that this triangle is similar to a \(3-4-5\) triangle. So the trig functions are the same.
An angle, \(\beta\), in a right triangle has hypotenuse and opposite side of lengths \(c=20\) and \(a=12\), respectively. Find the six trig functions for \(\beta\).

Remember SOH CAH TOA: \[\begin{aligned} \sin\beta&=\dfrac{\text{opp}}{\text{hyp}} \qquad \cos\beta&=\dfrac{\text{adj}}{\text{hyp}} \\ \tan\beta&=\dfrac{\text{opp}}{\text{adj}} \qquad \cot\beta&=\dfrac{\text{adj}}{\text{opp}} \\ \sec\beta&=\dfrac{\text{hyp}}{\text{adj}} \qquad \csc\beta&=\dfrac{\text{hyp}}{\text{opp}} \end{aligned}\] First calculate the length of the adjacent side using the Pythagorean Theorem, \(c^2=a^2+b^2\).

\(\begin{aligned} \sin\beta=\dfrac{3}{5} &\qquad \cos\beta=\dfrac{4}{5} \\ \tan\beta=\dfrac{3}{4} &\qquad \cot\beta=\dfrac{4}{3} \\ \sec\beta=\dfrac{5}{4} &\qquad \csc\beta=\dfrac{5}{3} \end{aligned}\)

The length of the adjacent side is calculated as such: \[\begin{aligned} b^{2}&=c^{2}-a^{2} \\ b&=\sqrt{c^{2}-a^{2}} \\ b&=\sqrt{20^{2}-12^{2}}=\sqrt{400-144} \\ &=\sqrt{256}=16 \end{aligned}\] So, the opposite side has a length \(12\), the adjacent side a length \(16\), and the hypotenuse a length \(20\). Then: \[\begin{aligned} \sin\beta&=\dfrac{\text{opp}}{\text{hyp}}=\dfrac{12}{20}=\dfrac{3}{5} \\ \cos\beta&=\dfrac{\text{adj}}{\text{hyp}}=\dfrac{16}{20}=\dfrac{4}{5} \\ \tan\beta&=\dfrac{\text{opp}}{\text{adj}}=\dfrac{12}{16}=\dfrac{3}{4} \\ \cot\beta&=\dfrac{\text{adj}}{\text{opp}}=\dfrac{16}{12}=\dfrac{4}{3} \\ \sec\beta&=\dfrac{\text{hyp}}{\text{adj}}=\dfrac{20}{16}=\dfrac{5}{4} \\ \csc\beta&=\dfrac{\text{hyp}}{\text{opp}}=\dfrac{20}{12}=\dfrac{5}{3} \end{aligned}\]

aas
Assume \(\sin\alpha=\dfrac{8}{17}\) and \(\cos\alpha=\dfrac{15}{17}\). Find the other four trig functions \(\tan\alpha\), \(\sec\alpha\), \(\cot\alpha\), and \(\csc\alpha\) using the quotient and reciprocal identities.

Recall the identities: \[\begin{aligned} &\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}\quad &&\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha}=\dfrac{1}{\tan\alpha} \\[8pt] &\sec\alpha=\dfrac{1}{\cos\alpha}\quad &&\csc\alpha=\dfrac{1}{\sin\alpha} \end{aligned}\]

\(\begin{aligned} \tan\alpha=\dfrac{8}{15} &\qquad \cot\alpha=\dfrac{15}{8} \\ \sec\alpha=\dfrac{17}{15} &\qquad \csc\alpha=\dfrac{17}{8} \end{aligned}\)

\[\begin{aligned} \tan\alpha&=\dfrac{\sin\alpha}{\cos\alpha}= \dfrac{8}{17}\cdot\dfrac{17}{15}=\dfrac{8}{15} \\[7pt] \cot\alpha&=\dfrac{1}{\tan\alpha}=\dfrac{1}{\ \dfrac{8}{15}\ }=\dfrac{15}{8} \\[10pt] \sec\alpha&=\dfrac{1}{\cos\alpha}=\dfrac{1}{\ \dfrac{15}{17}\ }=\dfrac{17}{15} \\[10pt] \csc\alpha&=\dfrac{1}{\sin\alpha}=\dfrac{1}{\ \dfrac{8}{17}\ }=\dfrac{17}{8} \end{aligned}\]

aas
Assume \(\sec\beta=\dfrac{13}{5}\) and \(\csc\beta=\dfrac{13}{12}\). Find the other four trig functions \(\sin\beta\), \(\cos\beta\), \(\tan\beta\), and \(\cot\beta\) using the quotient and reciprocal identities.

Recall the identities: \[\begin{aligned} &\tan\beta=\dfrac{\sin\beta}{\cos\beta}\quad &&\cot\beta=\dfrac{\cos\beta}{\sin\beta}=\dfrac{1}{\tan\beta} \\[8pt] &\sec\beta=\dfrac{1}{\cos\beta}\quad &&\csc\beta=\dfrac{1}{\sin\beta} \end{aligned}\]

\(\begin{aligned} \sin\beta=\dfrac{12}{13} &\qquad \cos\beta=\dfrac{5}{13} \\ \tan\beta=\dfrac{12}{5} &\qquad \cot\beta=\dfrac{5}{12} \end{aligned}\)

\[\begin{aligned} \sin\beta&=\dfrac{1}{\csc\beta}=\dfrac{1}{\ \dfrac{13}{12}\ }&=\dfrac{12}{13} \\ \cos\beta&=\dfrac{1}{\sec\beta}=\dfrac{1}{\ \dfrac{13}{5}\ }&=\dfrac{5}{13} \\ \tan\beta&=\dfrac{\sin\beta}{\cos\beta}=\dfrac{12}{13}\cdot\dfrac{13}{5}&=\dfrac{12}{5} \\ \cot\beta&=\dfrac{1}{\tan\beta}=\dfrac{1}{\ \dfrac{12}{5}\ }&=\dfrac{5}{12} \end{aligned}\]

aas
Suppose \(\sin\theta=\dfrac{2}{\sqrt{13}}\). Find the other \(5\) trig functions.

What are the opposite side and hypotenuse of some triangle with \(\sin\theta=\dfrac{2}{\sqrt{13}}\)?

\(\begin{aligned} &&\cos\theta&=\dfrac{3}{\sqrt{13}} \\ \tan\theta&=\dfrac{2}{3} &\cot\theta&=\dfrac{3}{2} \\ \sec\theta&=\dfrac{\sqrt{13}}{3} &\csc\theta&=\dfrac{\sqrt{13}}{2} \end{aligned}\)

First recall that \(\sin\theta=\dfrac{\text{opp}}{\text{hyp}}\). So, for this example, the right triangle can have opposite side \(a=2\) and hypotenuse \(c=\sqrt{13}\). The length of the adjacent side, \(b\), may be calculated using the Pythagorean Theorem: \[\begin{aligned} b&=\sqrt{c^{2}-a^{2}} =\sqrt{\sqrt{13}^{2}-2^{2}} \\ &=\sqrt{13-4} =\sqrt{9}=3 \end{aligned}\] So, the opposite side has length \(2\), the adjacent side length \(3\), and the hypotenuse length \(\sqrt{13}\). Then: \[\begin{aligned} \cos\theta&=\dfrac{\text{adj}}{\text{hyp}}=\dfrac{3}{\sqrt{13}} \\ \tan\theta&=\dfrac{\text{opp}}{\text{adj}}=\dfrac{2}{3} \\ \cot\theta&=\dfrac{\text{adj}}{\text{opp}}=\dfrac{3}{2} \\ \sec\theta&=\dfrac{\text{hyp}}{\text{adj}}=\dfrac{\sqrt{13}}{3} \\ \csc\theta&=\dfrac{\text{hyp}}{\text{opp}}=\dfrac{\sqrt{13}}{2} \end{aligned}\]

aas
Suppose \(\tan\phi=\dfrac{\sqrt{5}}{2}\). Find the other \(5\) trig functions.

What are the opposite and adjacent sides of some triangle with \(\tan\phi=\dfrac{\sqrt{5}}{2}\)?

\(\begin{aligned} \sin\phi&=\dfrac{\sqrt{5}}{3} &\qquad \cos\phi&=\dfrac{2}{3} \\ &&\cot\phi&=\dfrac{2}{\sqrt{5}} \\ \sec\phi&=\dfrac{3}{2} &\qquad \csc\phi&=\dfrac{3}{\sqrt{5}} \end{aligned}\)

First recognize that \(\tan\phi=\dfrac{\text{opp}}{\text{adj}}\). So, for this example, the right triangle can have an opposite side \(a=\sqrt{5}\) and adjacent side \(b=2\). The length of the hypotenuse, \(c\), may be calculated using the Pythagorean Theorem: \[\begin{aligned} c&=\sqrt{a^{2}+b^{2}}=\sqrt{\sqrt{5}^2+2^2} \\ &=\sqrt{5+4}=\sqrt{9}=3 \end{aligned}\] So, the opposite side has length \(\sqrt{5}\), the adjacent side length \(2\), and the hypotenuse length \(3\). Then: \[\begin{aligned} \sin\phi&=\dfrac{\text{opp}}{\text{hyp}}=\dfrac{\sqrt{5}}{3} \\ \cos\phi&=\dfrac{\text{adj}}{\text{hyp}}=\dfrac{2}{3} \\ \cot\phi&=\dfrac{\text{adj}}{\text{opp}}=\dfrac{2}{\sqrt{5}} \\ \sec\phi&=\dfrac{\text{hyp}}{\text{adj}}=\dfrac{3}{2} \\ \csc\phi&=\dfrac{\text{hyp}}{\text{opp}}=\dfrac{3}{\sqrt{5}} \end{aligned}\]

aas

c. Circle Definitions

What are the coordinates of a point on a circle of radius \(4\) at an angle of \(60^\circ\)?

Remember that if \((x,y)\) is the point on a circle with radius \(r\) at angle \(\theta\) then its coordinates are: \[ x=r\cos\theta \qquad \text{and} \qquad y=r\sin\theta \]

\((x,y)=(2,2\sqrt{3})\)

Use the formula for finding the coordinates \((x,y)\) for a point on a circle with radius \(r\) at angle \(\theta\): \[\begin{aligned} x&=r\cos\theta &\qquad y&=r\sin\theta \\ &=4(\cos60^\circ) &\qquad &=4(\sin60^\circ) \\ &=4\left(\dfrac{1}{2}\right) &\qquad &=4\left(\dfrac{\sqrt{3}}{2}\right) \\ &=2 &\qquad &=2\sqrt{3} \end{aligned}\]

aas
What are the coordinates of a point on a circle of radius \(8\) at an with an angle of \(45^\circ\)?

Remember that if \((x,y)\) is the point on a circle with radius \(r\) at angle \(\theta\) then its coordinates are: \[ (x,y)=(r\cos\theta,r\sin\theta) \]

\((x,y)=(4\sqrt{2},4\sqrt{2})\)

Use the formula for finding the coordinates \((x,y)\) for a point on a circle with radius \(r\) at angle \(\theta\): \[\begin{aligned} (x,y)&=(r\cos\theta,r\sin\theta) \\ &=(8\cos45^\circ,8\sin45^\circ) \\ &=\left(8\dfrac{\sqrt{2}}{2},8\dfrac{\sqrt{2}}{2}\right) =(4\sqrt{2},4\sqrt{2}) \end{aligned}\]

aas
There is a point on a circle with coordinates \((-5,5\sqrt{3})\).
1. What is the radius \(r\) of the circle?
  
  Remember the radius \(r\) of a circle is: \[ r=\sqrt{x^{2}+y^{2}} \]
  
  \(r=10\)
  
  For the point \((x,y)=(-5,5\sqrt{3})\), we can use the Pythagorean Theorem to find \(r\): \[\begin{aligned} r&=\sqrt{x^{2}+y^{2}}=\sqrt{(-5)^{2}+(5\sqrt{3})^2} \\ &=\sqrt{25+75}=\sqrt{100}=10 \end{aligned}\]
  
  aas
2. What are the coordinates of a point on this circle at the angle \(\theta=135^\circ\)?
  
  Remember that if \((x,y)\) is the point on a circle with radius \(r\) at angle \(\theta\) then its coordinates are: \[ (x,y)=(r\cos\theta,r\sin\theta) \]
  
  \((x,y)=(-5\sqrt{2},5\sqrt{2})\)
  
  Use the formula for finding the coordinates \((x,y)\) for a point on a circle with radius \(r\) at angle \(\theta\): \[\begin{aligned} (x,y)&=(r\cos\theta,r\sin\theta) \\ &=(10\cos135^\circ,10\sin135^\circ) \\ &=\left(10\dfrac{-\sqrt{2}}{2},10\dfrac{\sqrt{2}}{2}\right) =(-5\sqrt{2},5\sqrt{2}) \end{aligned}\]
  
  aas
If two angles of a triangle are \(45^\circ\) and the length of the side between them is \(6\,\text{in}\), find the third angle and the lengths of the other two sides.

The third angle is \(90^\circ\).
The other two sides are \(3\sqrt{2}\,\text{in}\approx4.243\,\text{in}\).

Given that the angles of a triangle must sum to \(180^\circ\), we know that the third angle in the triangle must be: \[ 180^\circ - 45^\circ - 45^\circ = 90^\circ \] We see that this is a traditional \(45/45/90\) triangle with sides in the ratio \(1,1,\sqrt{2}\). Here the hypotenuse is \(6\). So the other two sides of the triangle must be: \[ 3\sqrt{2}\,\text{in}\approx4.243\,\text{in} \]
In a circle, consider a ray at the angle \(\alpha\) which passes through the point \((0.3,0.4)\). Identify the six trig functions for the angle \(\alpha\).

If the ray passes through the point \((0.3,0.4)\), what is the radius?

\(\begin{aligned} \sin\alpha=\dfrac{4}{5} &\qquad \cos\alpha=\dfrac{3}{5} \\ \tan\alpha=\dfrac{4}{3} &\qquad \cot\alpha=\dfrac{3}{4} \\ \sec\alpha=\dfrac{5}{3} &\qquad \csc\alpha=\dfrac{5}{4} \end{aligned}\)

For the point \((0.3,0.4)\), we have \[ x=0.3 \qquad y=0.4 \qquad r=\sqrt{(.3)^2+(.4)^2}=0.5 \] Therefore, the trig functions are: \[\begin{aligned} \sin\alpha&=\dfrac{y}{r}=\dfrac{0.4}{0.5}=\dfrac{4}{5} \\[5pt] \cos\alpha&=\dfrac{x}{r}=\dfrac{0.3}{0.5}=\dfrac{3}{5} \\[5pt] \tan\alpha&=\dfrac{y}{x}=\dfrac{0.4}{0.3}=\dfrac{4}{3} \\[5pt] \cot\alpha&=\dfrac{x}{y}=\dfrac{0.3}{0.4}=\dfrac{3}{4} \\[5pt] \sec\alpha&=\dfrac{r}{x}=\dfrac{0.5}{0.3}=\dfrac{5}{3} \\[5pt] \csc\alpha&=\dfrac{r}{y}=\dfrac{0.5}{0.4}=\dfrac{5}{4} \end{aligned}\]

aas
In a circle, consider a ray at the angle \(\beta\) which passes through the point \((0.5,1.2)\). Identify the six trig functions for the angle \(\beta\).

If the ray passes through the point \((0.5,1.2)\), what is the radius?

\(\begin{aligned} \sin\beta=\dfrac{12}{13} &\qquad \cos\beta=\dfrac{5}{13} \\ \tan\beta=\dfrac{12}{5} &\qquad \cot\beta=\dfrac{5}{12} \\ \sec\beta=\dfrac{13}{5} &\qquad \csc\beta=\dfrac{13}{12} \end{aligned}\)

For the point \((0.5,1.2)\), we have \[ x=0.5 \qquad y=1.2 \qquad r=\sqrt{(.5)^2+(1.2)^2}=\sqrt{1.69}=1.3 \] Therefore, the trig functions are: \[\begin{aligned} \sin\beta&=\dfrac{y}{r}=\dfrac{1.2}{1.3}=\dfrac{12}{13} \\[5pt] \cos\beta&=\dfrac{x}{r}=\dfrac{0.5}{1.3}=\dfrac{5}{13} \\[5pt] \tan\beta&=\dfrac{y}{x}=\dfrac{1.2}{0.5}=\dfrac{12}{5} \\[5pt] \cot\beta&=\dfrac{x}{y}=\dfrac{0.5}{1.2}=\dfrac{5}{12} \\[5pt] \sec\beta&=\dfrac{r}{x}=\dfrac{1.3}{0.5}=\dfrac{13}{5} \\[5pt] \csc\beta&=\dfrac{r}{y}=\dfrac{1.3}{1.2}=\dfrac{13}{12} \end{aligned}\]

aas
In a circle, consider a ray at the angle \(\theta\) which passes through the point \((1.2,-0.9)\). Identify the six trig functions for the angle \(\theta\).

If the ray passes through the point \((1.2,-0.9)\), what is the radius?

\(\begin{aligned} \sin\theta&=-\,\dfrac{3}{5} &\qquad \cos\theta&=\dfrac{4}{5} \\ \tan\theta&=-\,\dfrac{3}{4} &\qquad \cot\theta&=-\,\dfrac{4}{3} \\ \sec\theta&=\dfrac{5}{4} &\qquad \csc\theta&=-\,\dfrac{5}{3} \end{aligned}\)

For the point \((1.2,-0.9)\), we have \[ x=1.2 \qquad y=-0.9 \qquad r=\sqrt{(1.2)^2+(-0.9)^2}=\sqrt{2.25}=1.5 \] Therefore, the trig functions are: \[\begin{aligned} \sin\theta&=\dfrac{y}{r}=\dfrac{-0.9}{1.5}=-\,\dfrac{3}{5} \\[5pt] \cos\theta&=\dfrac{x}{r}=\dfrac{1.2}{1.5}=\dfrac{4}{5} \\[5pt] \tan\theta&=\dfrac{y}{x}=\dfrac{-0.9}{1.2}=-\,\dfrac{3}{4} \\[5pt] \cot\theta&=\dfrac{x}{y}=\dfrac{1.2}{-0.9}=-\,\dfrac{4}{3} \\[5pt] \sec\theta&=\dfrac{r}{x}=\dfrac{1.5}{1.2}=\dfrac{5}{4} \\[5pt] \csc\theta&=\dfrac{r}{y}=\dfrac{1.5}{-0.9}=-\,\dfrac{5}{3} \end{aligned}\]

aas
In a circle, consider a ray at the angle \(\phi\) which passes through the point \((-0.8,-0.6)\). Identify the six trig functions for the angle \(\phi\).

If the ray passes through the point \((-0.8,-0.6)\), what is the radius?

\(\begin{aligned} \sin\phi&=-\,\dfrac{3}{5} &\qquad \cos\phi&=-\,\dfrac{4}{5} \\ \tan\phi&=\dfrac{3}{4} &\qquad \cot\phi&=\dfrac{4}{3} \\ \sec\phi&=-\,\dfrac{5}{4} &\qquad \csc\phi&=-\,\dfrac{5}{3} \end{aligned}\)

For the point \((-0.8,-0.6)\), we have \[ x=-0.8 \qquad y=-0.6 \qquad r=\sqrt{(-0.8)^2+(-0.6)^2}=1 \] Therefore, the trig functions are: \[\begin{aligned} \sin\phi&=\dfrac{y}{r}=\dfrac{-0.6}{1}=-\,\dfrac{3}{5} \\[5pt] \cos\phi&=\dfrac{x}{r}=\dfrac{-0.8}{1}=-\,\dfrac{4}{5} \\[5pt] \tan\phi&=\dfrac{y}{x}=\dfrac{-0.6}{-0.8}=\dfrac{3}{4} \\[5pt] \cot\phi&=\dfrac{x}{y}=\dfrac{-0.8}{-0.6}=\dfrac{4}{3} \\[5pt] \sec\phi&=\dfrac{r}{x}=\dfrac{1}{-0.8}=-\,\dfrac{5}{4} \\[5pt] \csc\phi&=\dfrac{r}{y}=\dfrac{1}{-0.6}=-\,\dfrac{5}{3} \end{aligned}\]

aas
If the radius of a circle is \(r=20\), what are the coordinates of the point in the second quadrant where \(\sin\theta=0.8\)?

Since the point is in the second quadrant, what will the signs of the x and y coordinates be?

\((-12,16)\)

We know that \(\sin\theta=\dfrac{y}{r}\). We also know that \(\sin\theta=0.8\) and \(r=20\). So, we solve for \(y\): \[\begin{aligned} 0.8&=\dfrac{y}{20} \\ y&=16 \end{aligned}\] To find \(x\), we use the Pythagorean theorem: \[\begin{aligned} x^{2}&=r^{2}-y^{2} \\ x&=\sqrt{r^{2}-y^{2}}=\sqrt{20^{2}-16^{2}} \\ &=\sqrt{400-256}=\sqrt{144}=\pm12 \end{aligned}\] Finally, since this point is in the second quadrant, the \(x\)-coordinate must be negative while the \(y\)-coordinate must be positive. So, the coordinates of the point are \((-12,16)\).

aas
If the radius of a circle is \(r=5\), what are the coordinates of the point in the third quadrant where \(\sin\theta=-0.6\)?

Since the point is in the third quadrant, what will the signs of the x and y coordinates be?

\((-4,-3)\)

We know that \(\sin\theta=\dfrac{y}{r}\). We also know that \(\sin\theta=-0.6\) and \(r=5\). So, we solve for \(y\): \[\begin{aligned} -0.6&=\dfrac{y}{5} \\ y&=-3 \end{aligned}\] To find \(x\), we use the Pythagorean theorem: \[\begin{aligned} x^{2}&=r^{2}-y^{2} \\ x&=\sqrt{r^{2}-y^{2}}=\sqrt{5^{2}-(-3)^{2}} \\ &=\sqrt{25-9}=\sqrt{16}=\pm4 \end{aligned}\] Finally, since this point is in the third quadrant, both the \(x\) and \(y\) coordinate will be negative. So, the coordinates of the point are \((-4,-3)\).

aas
If \(\sin\theta=0.6\), what is the radius of the circle?

Recall that \(\sin\theta=\dfrac{y}{r}\).

You can't tell!

We know that \(\sin\theta=\dfrac{y}{r}\). To have \(\sin\theta=0.6\), We need \(\dfrac{y}{r}=0.6\). This says, \(r\) could be ANY value so long as \(y=0.6r\). So there is no unique answer for the radius!

aas

d. Trig Identities

Suppose \(\sin\alpha=0.6\) and \(\alpha\) is in the first quadrant. Find the other five trig functions of the angle \(\alpha\).
Note: Use the identities. Don't first find the sides of a triangle where \(\sin\alpha=0.6\).

Remember the Pythagorean Identity for Sine and Cosine: \(\sin^{2}\alpha+\cos^{2}\alpha=1\).

\(\begin{aligned} \sin\alpha&=0.6 &\qquad \cos\alpha&=0.8 \\ \tan\alpha&=0.75 &\qquad \cot\alpha&=1.3\bar3 \\ \sec\alpha&=1.25 &\qquad \csc\alpha&=1.6\bar6 \end{aligned}\)

We first find \(\cos\alpha\). By the Pythagorean Identity for Sine and Cosine, we know that \(\sin^{2}\alpha+\cos^{2}\alpha=1\). Rearranging, we see that \[\begin{aligned} \sqrt{1-\sin^{2}\alpha}=\sqrt{\cos^{2}\alpha}=\pm\cos\alpha \end{aligned}\] Since \(\alpha\) is in the first quadrant, \(\cos\alpha\) must be positive. So we take the plus sign. Substituting \(\sin\alpha=0.6\), we have: \[\begin{aligned} \cos\alpha=\sqrt{1-\sin^{2}\alpha}=\sqrt{1-0.36}=\sqrt{0.64}=0.8 \end{aligned}\] We know that \(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}\), therefore: \[\begin{aligned} \tan\alpha=\dfrac{0.6}{0.8}=\dfrac{3}{4}=0.75 \end{aligned}\] Similarly, we have: \[\begin{aligned} \cot\alpha&=\dfrac{1}{\tan\alpha}=\dfrac{1}{0.75}=\dfrac{4}{3}=1.3\bar3 \\ \sec\alpha&=\dfrac{1}{\cos\alpha}=\dfrac{1}{0.8}=\dfrac{5}{4}=1.25 \\ \csc\alpha&=\dfrac{1}{\sin\alpha}=\dfrac{1}{0.6}=\dfrac{5}{3}=1.6\bar6 \end{aligned}\]

aas
Suppose \(\tan\beta=0.75\) and \(\beta\) is in the third quadrant. Find the other five trig functions of the angle \(\beta\).
Note: Use the identities. Don't first find the sides of a triangle where \(\tan\beta=0.75\).

Remember the Pythagorean Identity for Tangent and Secant: \(\tan^{2}+1=\sec^{2}\).

\(\begin{aligned} \sin\beta&=-0.6 &\qquad \cos\beta&=-0.8 \\ \tan\beta&=0.75 &\qquad \cot\beta&=1.3\bar3 \\ \sec\beta&=-1.25 &\qquad \csc\beta&=-1.6\bar6 \end{aligned}\)

In the third quadrant, \(\sin\beta\) and \(\cos\beta\) are negative because \(x\) and \(y\) are negative. So \(\sec\beta\) and \(\csc\beta\) are negative while \(\tan\beta\) and \(\cot\beta\) are positive. Also notice \(\tan\beta=0.75=\dfrac{3}{4}\).
The simplest is \(\cot\beta\): \[ \cot\beta=\dfrac{1}{\tan\beta} =\dfrac{1}{\;\dfrac{\rule{0pt}{8pt}3}{4}\;}=\dfrac{4}{3}=1.3\bar3 \] Next we find \(\sec\beta\). By the Pythagorean Identity for Tangent and Secant, we know that \(\tan^{2}\beta+1=\sec^{2}\beta\). Rearranging, we see that \[ \sec\beta=\pm\sqrt{\tan^{2}\beta+1} \] For the third quadrant, we take the minus sign. Substituting \(\tan\beta=\dfrac{3}{4}\), we have: \[\begin{aligned} \sec\beta&=-\sqrt{\tan^{2}\beta+1}=-\sqrt{\left(\dfrac{3}{4}\right)^{2}+1} \\ &=-\sqrt{\dfrac{9}{16}+1}=-\sqrt{\dfrac{25}{16}}=-\,\dfrac{5}{4}=-1.25 \end{aligned}\] For \(\cos\beta\) we have: \[ \cos\beta=\dfrac{1}{\sec\beta}=\dfrac{1}{\;-\dfrac{\rule{0pt}{8pt}5}{4}\;} =-\dfrac{4}{5}=-0.8 \] We also know that \(\sin^{2}\beta+\cos^{2}\beta=1\). So, rearranging, can evaluate \(\sin\beta\), which must also be negative: \[\begin{aligned} \sin\beta&=-\sqrt{1-\cos^{2}\beta}=-\sqrt{1-\left(\dfrac{4}{5}\right)^{2}} \\ &=-\sqrt{1-\dfrac{16}{25}}=-\sqrt{\dfrac{9}{25}}=-\,\dfrac{3}{5}=-0.6 \end{aligned}\] Finally, we find \(\csc\beta\): \[ \csc\beta=\dfrac{1}{\sin\beta}=\dfrac{1}{\;-\,\dfrac{\rule{0pt}{8pt}3}{5}\;} =-\dfrac{5}{3}=-1.6\bar6 \]

aas

There is another way to find \(\sin\beta\) in the context of this problem. Instead of using the Pythagorean Identity \(\sin^{2}\beta+\cos^{2}\beta=1\), you can use the Quotient Identity \(\tan\beta=\dfrac{\sin\beta}{\cos\beta}\). Then: \[ \sin\beta=\tan\beta\cos\beta =-\,\dfrac{3}{4}\cdot\dfrac{4}{5}=-\,\dfrac{3}{5} \]
Find \(\sin105^\circ\).

Notice \(105^\circ=45^\circ+60^\circ\). Use the Sum of Angles identity.

\(\sin105^\circ=\dfrac{\sqrt{2}}{4}\left(1+\sqrt{3}\right)\)

We first recognize that \(105^\circ=45^\circ+60^\circ\), so \(\sin105^\circ\) can be rewritten as \(\sin(45^\circ+60^\circ)\). We then use the Sum Identity for Sine: \[\begin{aligned} \sin(A+B)&=\sin(A)\cos(B)+\cos(A)\sin(B) \\ \sin(45^\circ+60^\circ)&=(\sin45^\circ)(\cos60^\circ)+(\cos45^\circ)(\sin60^\circ) \\ \sin105^\circ&=\left(\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{1}{2}\right)+\left(\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{\sqrt{3}}{2}\right) \\ &=\dfrac{\sqrt{2}}{4}\left(1+\sqrt{3}\right) \end{aligned}\]

aas
Find \(\cos165^\circ\).

Notice \(165^\circ=120^\circ+45^\circ\). Use a Sum of Angles identity.

\(\cos165^\circ=-\,\dfrac{\sqrt{2}}{4}\left(1+\sqrt{3}\right)\)

We first recognize that \(165^\circ=120^\circ+45^\circ\), so we use the Sum Identity for Cosine: \[\begin{aligned} \cos(A+B)&=\cos(A)\cos(B)-\sin(A)\sin(B) \\ \cos(120^\circ+45^\circ) &=\cos(120^\circ)\cos(45^\circ)-\sin(120^\circ)\sin(45^\circ) \\ \cos165^\circ&=\left(-\dfrac{1}{2}\right)\left(\dfrac{\sqrt{2}}{2}\right)-\left(\dfrac{\sqrt{3}}{2}\right)\left(\dfrac{\sqrt{2}}{2}\right)\\ &=-\,\dfrac{\sqrt{2}}{4}\left(1+\sqrt{3}\right) \end{aligned}\] For a review of \(\sin(120^\circ)\) and \(\cos(120^\circ)\) see Review of trig functions for bigger angles.

aas

There are many ways to do this problem. For instance, we could also write \[ 165^\circ=210^\circ-45^\circ \] and use a Difference of Angles identity.
Find \(\tan195^\circ\).

Notice \(195^\circ=135^\circ+60^\circ\). Use a Sum of Angles identity.

\(\tan195^\circ=\dfrac{-1+\sqrt{3}}{1+\sqrt{3}}=2-\sqrt{3}\)

We first recognize that \(195^\circ=135^\circ+60^\circ\), so we can use the Sum Identity for Tangent: \[\begin{aligned} \tan(A+B)&=\dfrac{\tan(A)+\tan(B)}{1-\tan(A)\tan(B)} \\ \tan(135^\circ+60^\circ) &=\dfrac{\tan(135^\circ)+\tan(60^\circ)}{1-\tan(135^\circ)\tan(60^\circ)} \end{aligned}\] We now need to know \(\tan(135^\circ)\). Since \(135^\circ\) is in the \(2^\text{nd}\) quadrant, behaves like \(45^\circ\) but there is a sign change. Since \(\tan(45^\circ)=1\), \(\tan(135^\circ)=-1\). Thus: \[\begin{aligned} \tan195^\circ&=\dfrac{-1+\sqrt{3}}{1-(-1)(\sqrt{3})} \\ &=\dfrac{-1+\sqrt{3}}{1+\sqrt{3}} \end{aligned}\] If your teacher expects this to be rationalized, here it is: \[\begin{aligned} \tan195^\circ &=\dfrac{-1+\sqrt{3}}{1+\sqrt{3}}\cdot\dfrac{-1+\sqrt{3}}{-1+\sqrt{3}} \\ &=\dfrac{1-2\sqrt{3}+3}{3-1} \\ &=\dfrac{4-2\sqrt{3}}{2} =2-\sqrt{3} \end{aligned}\]

aas

There are many ways to do this problem. For instance, we could also write \[ 195^\circ=240^\circ-45^\circ \] or \[ 195^\circ=225^\circ-30^\circ \] and use a Difference of Angles identity.
Find \(\sin75^\circ\).

Notice \(75^\circ=120^\circ-45^\circ\). Use a Difference of Angles identity.

\(\sin75^\circ=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)

We first recognize that \(75^\circ=120^\circ-45^\circ\), so \(\sin75^\circ\) can be rewritten as \(\sin(120^\circ-45^\circ)\). We use the Difference Identity for Sine: \[\begin{aligned} \sin(A-B)&=\sin(A)\cos(B)-\cos(A)\sin(B) \\ \sin(120^\circ-45^\circ)&=\sin(120^\circ)\cos(45^\circ)-\cos(120^\circ)\sin(45^\circ) \\ \sin75^\circ&=\left(\dfrac{\sqrt{3}}{2}\right)\left(\dfrac{\sqrt{2}}{2}\right)- \left(-\dfrac{1}{2}\right)\left(\dfrac{\sqrt{2}}{2}\right) \\ &=\dfrac{\sqrt{6}+\sqrt{2}}{4} \end{aligned}\]

aas

There are other ways to do this problem. For instance, we could also write \[ 75^\circ=45^\circ+30^\circ \] and use a Sum of Angles identity.
Find \(\cos285^\circ\).

Notice \(285^\circ=240^\circ+45^\circ\). Use a Sum of Angles identity.

\(\cos285^\circ=\dfrac{\sqrt{6}-\sqrt{2}}{4}\)

We first recognize that \(285^\circ=240^\circ+45^\circ\), so \(\cos285^\circ\) can be rewritten as \(\cos(240^\circ+45^\circ)\). We use the Sum Identity for Cosine: \[\begin{aligned} \cos(A+B)&=\cos(A)\cos(B)-\sin(A)\sin(B) \\ \cos(240^\circ+45^\circ)&=\cos(240^\circ)\cos(45^\circ)-\sin(240^\circ)\sin(45^\circ) \\ \cos285^\circ&=\left(-\dfrac{1}{2}\right)\left(\dfrac{\sqrt{2}}{2}\right)-\left(-\dfrac{\sqrt{3}}{2}\right)\left(\dfrac{\sqrt{2}}{2}\right) \\ &=\dfrac{\sqrt{6}-\sqrt{2}}{4} \end{aligned}\]

aas

There are other ways to do this problem. For instance, we could also write \[ 285^\circ=330^\circ-45^\circ \] and use a Difference of Angles identity or \[ 285^\circ=225^\circ+60^\circ \] and use a Sum of Angles identity.
Find \(\tan15^\circ\).

Notice \(15^\circ=45^\circ-30^\circ\). Use a Difference of Angles identity.

\(\tan15^\circ=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}=2-\sqrt{3}\)

We first recognize that \(15^\circ=45^\circ-30^\circ\), so we can use the Difference Identity for Tangent: \[\begin{aligned} \tan(A-B)&=\dfrac{\tan(A)-\tan(B)}{1+\tan(A)\tan(B)} \\ \tan(45^\circ-30^\circ)&=\dfrac{\tan(45^\circ)-\tan(30^\circ)}{1+\tan(45^\circ)\tan(30^\circ)} \\ \tan15^\circ&=\dfrac{1-\dfrac{1}{\sqrt{3}}}{1+1\left(\dfrac{1}{\sqrt{3}}\right)} \\ &=\dfrac{\sqrt{3}-1}{\sqrt{3}+1} \end{aligned}\] If your teacher expects the denominator to be rationalized, here it is: \[\begin{aligned} \tan15^\circ&=\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\cdot\dfrac{\sqrt{3}-1}{\sqrt{3}-1} \\ &=\dfrac{3-2\sqrt{3}+1}{3-1} \\ &=\dfrac{4-2\sqrt{3}}{2} \\ &=2-\sqrt{3} \end{aligned}\]

aas
Consider an isosceles triangle with angles \(120^\circ\), \(30^\circ\), and \(30^\circ\), and a side of length \(a=6\) opposite the \(120^\circ\) angle. What are the lengths, \(b\) and \(c\), of the triangle's other two sides?

Remember the Law of Sines: \(\dfrac{\sin(A)}{a}=\dfrac{\sin(B)}{b}=\dfrac{\sin(C)}{c}\)

\(b=c=2\sqrt{3}\)

We use the Law of Sines: \[ \dfrac{\sin(A)}{a}=\dfrac{\sin(B)}{b}=\dfrac{\sin(C)}{c} \] And plug in the values we know: \[\begin{aligned} \dfrac{\sin(120^\circ)}{6}&=\dfrac{\sin(30^\circ)}{b}=\dfrac{\sin(30^\circ)}{c} \\ \dfrac{\;\;\dfrac{\sqrt{3}}{2}\;\;}{6} &=\dfrac{\;\;\dfrac{1}{2}\;\;}{b}=\dfrac{\;\;\dfrac{1}{2}\;\;}{c} \\ \dfrac{\sqrt{3}}{12}&=\dfrac{1}{2b}=\dfrac{1}{2c} \end{aligned}\] We now solve for \(b\) and \(c\) by cross multiplication: \[ b=c=\dfrac{6}{\sqrt{3}}=2\sqrt{3} \]

aas

Alternatively, drop a perpendicular from the \(120^\circ\) angle, splitting the triangle into two \(30-60-90\) triangles with the side opposite the \(60^\circ\) angle having length \(\dfrac{a}{2}=3\). Since the sides are in the ratios \(1,2,\sqrt{3}\), and \(b\) is the hypotenuse, we have: \[ \dfrac{b}{3}=\dfrac{2}{\sqrt{3}} \quad \text{or} \quad b=2\sqrt{3} \]
Consider an obtuse triangle with sides of lengths \(a=4\) and \(b=2\) that have a \(135^\circ\) angle between them. What is the length, \(c\), of the triangle's other side?

Remember the Law of Cosines: \(c^{2}=a^{2}+b^{2}-2ab\cos C\)

\(c=\sqrt{20+8\sqrt{2}}\)

We use the Law of Cosines and rearrange to isolate \(c\): \[\begin{aligned} c^{2}&=a^{2}+b^{2}-2ab\cos C \\ c&=\sqrt{a^{2}+b^{2}-2ab\cos C} \end{aligned}\] Then, we plug in the values we know and simplify: \[\begin{aligned} c&=\sqrt{4^{2}+2^{2}-2(4\cdot2)\cos(135^\circ)} \\ &=\sqrt{16+4-16\left(-\dfrac{\sqrt{2}}{2}\right)} \\ &=\sqrt{20+8\sqrt{2}} \end{aligned}\]

aas
Find \(\sin^{2}(22.5^\circ)\).

Use the Square Identity for Sine: \(\sin^{2}(A)=\dfrac{1-\cos(2A)}{2}\).

\(\sin^{2}22.5^\circ=\dfrac{2-\sqrt{2}}{4}\)

We recognize that \(45^\circ=2\cdot22.5^\circ\), so we can use the Square Identity for Sine: \[\begin{aligned} \sin^{2}(A)&=\dfrac{1-\cos(2A)}{2} \\ \sin^{2}22.5^\circ&=\dfrac{1-\cos45^\circ}{2} \\ &=\dfrac{1-\dfrac{\sqrt{2}}{2}}{2} \\ &=\dfrac{2-\sqrt{2}}{4} \end{aligned}\]

aas
Find \(\cos^{2}(67.5^\circ)\).

Use the Square Identity for Cosine: \(\cos^{2}(A)=\dfrac{1+\cos(2A)}{2}\).

\(\cos^{2}67.5^\circ=\dfrac{2-\sqrt{2}}{4}\)

We recognize that \(135^\circ=2\cdot67.5^\circ\), so we can use the Square Identity for Cosine: \[\begin{aligned} \cos^{2}(A)&=\dfrac{1+\cos(2A)}{2} \\ \cos^{2}67.5^\circ&=\dfrac{1+\cos(135^\circ)}{2} \\ &=\dfrac{1+\left(-\dfrac{\sqrt{2}}{2}\right)}{2} \\ &=\dfrac{2-\sqrt{2}}{4} \end{aligned}\]

aas

Notice the answer to this problem is the same as that for the previous problem. This is because \(67.5^\circ\) and \(22.5^\circ\) are complementary angles (i.e. \(67.5^\circ+22.5^\circ=90^\circ\)). Consequently, \(\cos67.5^\circ=\sin22.5^\circ\).
Find \(\sin(-30^\circ)\).

Use the Parity Identity for Sine: \(\sin(-\theta)=-\sin\theta\).

\(\sin(-30^\circ)=-\dfrac{1}{2}\)

Use the Parity Identity for Sine: \[\begin{aligned} \sin(-\theta)&=-\sin\theta \\ \sin(-30^\circ)&=-\sin30^\circ \\ \sin(-30^\circ)&=-\dfrac{1}{2} \end{aligned}\]

aas
Find \(\cos(-45^\circ)\).

Use the Parity Identity for Cosine: \(\cos(-\theta)=\cos\theta\).

\(\cos(-45^\circ)=\dfrac{\sqrt{2}}{2}\)

Use the Parity Identity for Cosine: \[\begin{aligned} \cos(-\theta)&=\cos\theta \\ \cos(-45^\circ)&=\cos45^\circ \\ \cos(-45^\circ)&=\dfrac{\sqrt{2}}{2} \end{aligned}\]

aas
Assume \(\alpha\) is in the \(1^\text{st}\) quadrant and \(\sin(\alpha)=0.6\). Find \(\sin(2\alpha)\).

Use the Double Angle Identity for Sine: \(\sin(2\alpha)=2\sin \alpha \cos \alpha\)

\(\sin(2\alpha)=0.96\)

We use the Double Angle Identity for Sine: \[ \sin(2\alpha)=2\sin \alpha\cos \alpha \] Since we know the value of \(\sin \alpha\), we need to find \(\cos \alpha\). By the Pythagorean Theorem \[ \cos \alpha=\sqrt{1-\sin^2\alpha}=\sqrt{1-.6^2}=\sqrt{.64}=.8 \] Finally, since we now know both \(\sin \alpha\) and \(\cos \alpha\), we evaluate \(\sin(2\alpha)\): \[\begin{aligned} \sin(2\alpha)&=2\sin \alpha\cos \alpha \\ &=2(0.6)(0.8) =0.96 \end{aligned}\]

aas
Assume \(\sin\beta=0.8\). Find \(\cos(2\beta)\).

Use the Double Angle Identity for Cosine: \[\begin{aligned} \cos(2\beta)&=\cos^{2}\beta-\sin^{2}\beta \\ &=2\cos^{2}\beta-1 \\ &=1-2\sin^{2}\beta \end{aligned}\]

\(\cos(2\beta)=-0.28\)

Since we know the value of \(\sin\beta\), we use the version of the Double Angle Identity for Cosine which only needs \(\sin\beta\): \[\begin{aligned} \cos(2\beta)&=1-2\sin^{2}\beta \\ &=1-2(0.8)^{2}=1-2(0.64) \\ &=1-1.28=-0.28 \end{aligned}\]

aas

e. Inverse Trig Functions

Find \(\arccos\left(\dfrac{\sqrt{3}}{2}\right)\).

By definition, \(\arccos(z)=\theta\) if \[ z=\cos(\theta) \qquad \text{and} \qquad 0 \le \theta \le \pi \]

\(\arccos\left(\dfrac{\sqrt{3}}{2}\right)=\dfrac{\pi}{6}\)

By definition, \(\arccos(z)=\theta\) if \[ z=\cos(\theta) \qquad \text{and} \qquad 0 \le \theta \le \pi \] Therefore \[ \arccos\left(\dfrac{\sqrt{3}}{2}\right)=\theta \qquad \text{means} \qquad \dfrac{\sqrt{3}}{2}=\cos(\theta) \] Since \[ \cos\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2} \] we conclude that \(\arccos\left(\dfrac{\sqrt{3}}{2}\right)=\dfrac{\pi}{6}\).

aas
Find \(\arcsin\left(-\dfrac{\sqrt{3}}{2}\right)\).

By definition, \(\arcsin(z)=\theta\) if \[ z=\sin(\theta) \qquad \text{and} \qquad -\dfrac{\pi}{2} \le \theta \le \dfrac{\pi}{2} \]

\(\arcsin\left(-\dfrac{\sqrt{3}}{2}\right)=-\dfrac{\pi}{3}\)

By definition, \(\arcsin(z)=\theta\) if \[ z=\sin(\theta) \qquad \text{and} \qquad -\dfrac{\pi}{2} \le \theta \le \dfrac{\pi}{2} \] Therefore \[ \arcsin\left(\dfrac{-\sqrt{3}}{2}\right)=\theta \qquad \text{means} \qquad \dfrac{-\sqrt{3}}{2}=\sin(\theta) \] Since \[ \sin\left(-\dfrac{\pi}{3}\right)=-\dfrac{\sqrt{3}}{2} \] we can conclude that \(\arcsin\left(-\dfrac{\sqrt{3}}{2}\right)=-\dfrac{\pi}{3}\).

aas
Find \(\arctan(-\sqrt{3})\).

By definition, \(\arctan(z)=\theta\) if \[ z=\tan(\theta) \qquad \text{and} \qquad -\dfrac{\pi}{2} \lt \theta \lt \dfrac{\pi}{2} \]

\(\arctan(-\sqrt{3})=-\dfrac{\pi}{3}\)

By definition, \(\arctan(z)=\theta\) if \[ z=\tan(\theta) \qquad \text{and} \qquad -\dfrac{\pi}{2} \lt \theta \lt \dfrac{\pi}{2} \] Therefore \[ \arctan(-\sqrt{3})=\theta \qquad \text{means} \qquad -\sqrt{3}=\tan(\theta) \] Since \[ \tan\left(-\dfrac{\pi}{3}\right)=-\sqrt{3} \] we can conclude that \(\arctan(-\sqrt{3})=-\dfrac{\pi}{3}\).

aas
Find \(\text{arccot}(-\sqrt{3})\).

By definition, \(\text{arccot}(z)=\theta\) if \[ z=\cot(\theta) \qquad \text{and} \qquad 0 \lt \theta \lt \pi \]

\(\text{arccot}(-\sqrt{3})=\dfrac{5\pi}{6}\)

By definition, \(\text{arccot}(z)=\theta\) if \[ z=\cot(\theta) \qquad \text{and} \qquad 0 \lt \theta \lt \pi \] Therefore \[ \text{arccot}(-\sqrt{3})=\theta \qquad \text{means} \qquad -\sqrt{3}=\cot(\theta) \] Since \[ \cot\left(\dfrac{5\pi}{6}\right)=-\sqrt{3} \] we can conclude that \(\text{arccot}(-\sqrt{3})=\dfrac{5\pi}{6}\)

aas
Find \(\text{arcsec}\left(\dfrac{2}{\sqrt{2}}\right)\).

By definition, \(\text{arcsec}(z)=\theta\) if \[ z=\sec(\theta) \qquad \text{and} \qquad 0 \le \theta \lt \dfrac{\pi}{2} \qquad \text{or} \qquad \dfrac{\pi}{2} \lt \theta \le \pi \]

\(\text{arcsec}\left(\dfrac{2}{\sqrt{2}}\right)=\dfrac{\pi}{4}\)

By definition, \(\text{arcsec}(z)=\theta\) if \[ z=\sec(\theta) \qquad \text{and} \qquad 0 \le \theta \lt \dfrac{\pi}{2} \qquad \text{or} \qquad \dfrac{\pi}{2} \lt \theta \le \pi \] Therefore \[ \text{arcsec}\left(\dfrac{2}{\sqrt{2}}\right)=\theta \qquad \text{means} \qquad \dfrac{2}{\sqrt{2}}=\sec(\theta) \] Equivalently, \(\cos(\theta)=\dfrac{\sqrt{2}}{2}\) and so \(\theta=\dfrac{\pi}{4}\). We conclude that \(\text{arcsec}\left(\dfrac{2}{\sqrt{2}}\right)=\dfrac{\pi}{4}\).

aas
Find \(\text{arccsc}(-2)\).

By definition, \(\text{arccsc}(z)=\theta\) if \[ z=\csc(\theta) \qquad \text{and} \qquad -\dfrac{\pi}{2} \le \theta \lt 0 \qquad \text{or} \qquad 0 \lt \theta \le \dfrac{\pi}{2} \]

\(\text{arccsc}(-2)=-\,\dfrac{\pi}{6}\)

By definition, \(\text{arccsc}(z)=\theta\) if \[ z=\csc(\theta) \qquad \text{and} \qquad -\dfrac{\pi}{2} \le \theta \lt 0 \qquad \text{or} \qquad 0 \lt \theta \le \dfrac{\pi}{2} \] Therefore \[ \text{arccsc}(-2)=\theta \qquad \text{means} \qquad -2=\csc(\theta) \] Equivalently, \(\sin(\theta)=-\,\dfrac{1}{2}\) and so \(\theta=-\,\dfrac{\pi}{6}\). We conclude that \(\text{arccsc}(-2)=-\,\dfrac{\pi}{6}\).

aas

f. Applications

An \(8\,\text{ft}\) ladder is leaning against a wall with \(3\,\text{ft}\) of space between the base of the ladder and the wall. If a \(24\,\text{ft}\) ladder were propped up against the wall at the same angle as the other ladder, how much space would there be between the \(24\,\text{ft}\) ladder's base and the wall?

Remember that if \(2\) triangles \(\triangle ABC\) and \(\triangle DEF\) are similar, then the ratios of corresponding sides are equal: \[ \dfrac{a}{d}=\dfrac{b}{e}=\dfrac{c}{f} \]

\(9\,\text{ft}\)

A ladder propped up against a wall creates a right triangle, with the ladder acting as the hypotenuse. If there are two ladders propped up against a wall while making the same angle with the ground, then the triangles they create are similar, since their corresponding angles are equal.

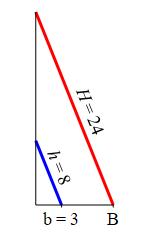
For the original ladder, the hypotenuse and base are \(h=8\,\text{ft}\) and \(b=3\,\text{ft}\). For the second ladder, the hypotenuse is \(H=24\,\text{ft}\) and let the base be \(B\). Since the triangles are similar, \[\begin{aligned} \dfrac{B}{b}&=\dfrac{H}{h} \\ \dfrac{B}{3}&=\dfrac{24}{8} \\ B&=9\,\text{ft} \end{aligned}\]

aas

In the following problems, you may use a calculator. Keep answers to \(2\) decimal places.

SAS: A triangle \(\triangle ABC\) has two sides of length \(b=4\,\text{in}\) and \(c=6\,\text{in}\). The angle between them is \(A=60^\circ\). Find the length of the third side and the other two angles.

Remember the Law of Sines: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] And the Law of Cosines: \[\begin{aligned} c^2=a^2+b^2-2ab\cos C \\ b^2=a^2+c^2-2ac\cos B \\ a^2=b^2+c^2-2bc\cos A \end{aligned}\]

\[\begin{aligned} a&=5.29\,\text{in} \\ B&=40.9^\circ \\ C&=79.1^\circ \end{aligned}\]

Using the Law of Cosines, we can find the third side, \(a\): \[\begin{aligned} a^2&=b^2+c^2-2bc\cos A \\ &=4^2+6^2-2\cdot4\cdot6\cos60^\circ \\ &=16+36-48\cdot\dfrac{1}{2}=28 \\ a&=\sqrt{28}\approx5.29 \end{aligned}\] The other two angles can be found either using the Law of Sines or the Law of Cosines. We'll use the Law of Sines. The angle \(B\) opposite \(b\) and the angle \(C\) opposite \(c\) satisfy: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] So: \[\begin{aligned} \sin B&=b\dfrac{\sin A}{a}=4\dfrac{\sin60^\circ}{5.29}\approx0.655 \\ B&=\arcsin(0.655)\approx40.9^\circ \\ \sin C&=c\dfrac{\sin A}{a}=6\dfrac{\sin60^\circ}{5.29}\approx0.982 \\ C&=\arcsin(0.982)\approx79.1^\circ \\ \end{aligned}\] Be sure to check the angles add up to \(180^\circ\).
If you'd like to see this portion done using the Law of Cosines, see the remark.

aas

We can check by adding up the angles to ensure they equal \(180^\circ\): \[ A+B+C=60^\circ+40.9^\circ+79.1^\circ=180^\circ \]

We can also use the Law of Cosines to find angle \(B\): \[\begin{aligned} b^2&=a^2+c^2-2ac\cos B \\ 4^2&=5.29^2+6^2-2\cdot5.29\cdot6\cos B \\ 16&=28+36-63.5\cos B \\ -48&=-63.5\cos B \\ \cos B&=0.756 \\ B&=\arccos(0.756)=40.9^\circ \end{aligned}\] Similarly, for angle \(C\): \[\begin{aligned} c^2&=a^2+b^2-2ab\cos C \\ 6^2&=5.29^2+4^2-2\cdot5.29\cdot4\cos C \\ 36&=28+16-42.3\cos C \\ -8&=-42.3\cos C\\ \cos C&=0.189 \\ C&=\arccos(0.189)=79.1^\circ \end{aligned}\]
ASA: A triangle \(\triangle ABC\) has two angles of \(A=30^\circ\) and \(B=45^\circ\). The side between them has length \(c=3\,\text{in}\). Find the third angle and the lengths of the other \(2\) sides.

You can use either the Law of Sines: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] or the Law of Cosines: \[\begin{aligned} c^2=a^2+b^2-2ab\cos C \\ b^2=a^2+c^2-2ac\cos B \\ a^2=b^2+c^2-2bc\cos A \end{aligned}\]

\(\begin{aligned} C&=105^\circ \\ a&=1.553\,\text{in} \\ b&=2.196\,\text{in} \end{aligned}\)

The third angle is found by subtracting from \(180^\circ\): \[ C=180^\circ-A-B=180^\circ-30^\circ-45^\circ=105^\circ \] The other \(2\) sides can be found using either the Law of Sines or the Law of Cosines. We'll use the Law of Sines. The sides satisfy: \[ \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C} \] So: \[\begin{aligned} a&=c\dfrac{\sin A}{\sin C}=3\dfrac{\sin 30^\circ}{\sin 105^\circ}\approx1.553 \\[5pt] b&=c\dfrac{\sin B}{\sin C}=3\dfrac{\sin 45^\circ}{\sin 105^\circ}\approx2.196 \end{aligned}\]

aas

We check using the Law of Cosines: \[\begin{aligned} c&=\sqrt{a^2+b^2-2ab\cos C} \\ &=\sqrt{1.553^2+2.196^2-2\cdot1.553\cdot2.196\cos105^\circ} \\ &\approx2.99993 \end{aligned}\] which is \(3\) allowing for calculator error.
SSS: A triangle \(\triangle ABC\) has sides \(a=4\,\text{m}\), \(b=6\,\text{m}\), and \(c=8\,\text{m}\). Find the \(3\) angles.

Remember the Law of Cosines: \[\begin{aligned} c^2&=a^2+b^2-2ab\cos C \\ b^2&=a^2+c^2-2ac\cos B \\ a^2&=b^2+c^2-2bc\cos A \end{aligned}\]

\(\begin{aligned} A&=28.96^\circ \\ B&=46.57^\circ \\ C&=104.48^\circ \end{aligned}\)

We will use the Law of Cosines to find the \(3\) angles: \[\begin{aligned} \cos A&=\dfrac{b^2+c^2-a^2}{2bc} \\ &=\dfrac{6^2+8^2-4^2}{2\cdot6\cdot8}=\dfrac{84}{96}=\dfrac{7}{8} \\ A&=\arccos\dfrac{7}{8}\approx28.96^\circ \\ \cos B&=\dfrac{c^2+a^2-b^2}{2ca} \\ &=\dfrac{8^2+4^2-6^2}{2\cdot8\cdot4}=\dfrac{44}{64}=\dfrac{11}{16} \\ B&=\arccos\dfrac{11}{16}\approx46.57^\circ \\ \cos C&=\dfrac{a^2+b^2-c^2}{2ab} \\ &=\dfrac{4^2+6^2-8^2}{2\cdot4\cdot6}=\dfrac{-12}{48}=-\dfrac{1}{4} \\ C&=\arccos\left(-\,\dfrac{1}{4}\right)\approx104.48^\circ \end{aligned}\]

aas

We check by adding up the angles: \[ 28.96^\circ+46.57^\circ+104.48^\circ=180.01^\circ \] which is \(180^\circ\) allowing for rounding error.
ASS: A triangle \(\triangle ABC\) has two sides of length \(a=5\,\text{cm}\) and \(b=4\,\text{cm}\). The angle opposite side \(b\) is \(B=45^\circ\). Find the other two angles \(A\) and \(C\), as well as the length of side \(c\).

Remember the Law of Sines: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] Check for \(2\) solutions for \(A\).

\(\begin{aligned} A_1&\approx62.11^\circ &C_1&\approx72.89^\circ &c_1&\approx5.41\,\text{cm} \\ A_2&\approx117.89^\circ &C_2&\approx17.11^\circ &c_2&\approx1.66\,\text{cm} \end{aligned}\)

We begin by using the Law of Sines to find the angle \(A\): \[\begin{aligned} \sin A&=\dfrac{a}{b}\sin B =\dfrac{5}{4}\sin45^\circ \\ &=\dfrac{5}{4}\left(\dfrac{\sqrt{2}}{2}\right) =\dfrac{5}{4\sqrt{2}} \end{aligned}\] There may be two solutions, one acute and one obtuse. The acute one is: \[ A_1=\arcsin\left(\dfrac{5}{4\sqrt{2}}\right)\approx62.11^\circ \] For this \(A_1\), we find the angle \(C_1\) by subtracting from \(180^\circ\): \[\begin{aligned} C_1&=180^\circ-A_1^\circ-B^\circ \\ &=180^\circ-62.11^\circ-45^\circ \\ &=72.89^\circ \end{aligned}\] Finally, we find the length \(c_1\) by again using the Law of Sines: \[\begin{aligned} c_1&=\dfrac{\sin C_1}{\sin B}b \\ &=\dfrac{\sin72.89^\circ}{\sin45^\circ}4 \\ &\approx5.41 \end{aligned}\] The obtuse solution is: \[\begin{aligned} A_2&=180^\circ-\arcsin\left(\dfrac{5}{4\sqrt{2}}\right) \\ &=180^\circ-62.11^\circ=117.89^\circ \end{aligned}\] Does this produce a second solution for a triangle? Let's try to find \(C_2\): \[\begin{aligned} C_2&=180^\circ-A_2-B \\ &=180^\circ-117.89^\circ-45^\circ \\ &=17.11^\circ \end{aligned}\] Since this is positive, there is a second triangle! Finally, we find the length \(c_2\) by using the Law of Sines: \[\begin{aligned} c_2&=\dfrac{\sin C_2}{\sin B}b \\ &=\dfrac{\sin17.11^\circ}{\sin45^\circ}4 \\ &\approx1.66 \end{aligned}\]

aas

We check by finding \(c\) using the Law of Cosines: \[\begin{aligned} c^2&=a^2+b^2-2ab\cos C \\ &=5^2+4^2-2\cdot5\cdot4\cos 72.89^\circ =29.23 \\ c&=5.41 \end{aligned}\] We then find \(c_2\), also using the Law of Cosines: \[\begin{aligned} c_2^2&=a^2+b^2-2ab\cos C_2 \\ &=5^2+4^2-2\cdot5\cdot4\cos 17.11^\circ =2.77 \\ c_2&=1.66 \end{aligned}\] These both agree with the results found using the Law of Sines.
ASS: A triangle \(\triangle ABC\) has two sides of length \(a=6\,\text{cm}\) and \(b=3\,\text{cm}\). The angle opposite side \(b\) is \(B=45^\circ\). Find the other two angles \(A\) and \(C\), as well as the length of side \(c\).

Remember the Law of Sines: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \]

There are \(0\) solutions for the angle \(A\), meaning that we cannot find solutions for the angle \(C\) or the length of side \(c\) either.

We begin by using the Law of Sines to find the angle \(A\): \[\begin{aligned} \sin A&=\dfrac{a}{b}\sin B =\dfrac{6}{3}\sin45^\circ \\ &=\dfrac{6}{3}\left(\dfrac{\sqrt{2}}{2}\right) =\sqrt{2} \gt 1 \end{aligned}\] Since \(\sin A \gt 1\), there are no solutions! Let's check the general condition for no solutions, i.e. \(b \lt a\sin B\): We have \(b=3\) and \(a\sin B=6\sin 45^\circ=3\sqrt2\approx4.24\). So \(b \lt a\sin B\). Consequently, there are no solutions for \(A\) and no triangles with these sides and angle.

aas
ASS: A triangle \(\triangle ABC\) has two sides of length \(a=6\,\text{cm}\) and \(b=3\,\text{cm}\). The angle opposite side \(b\) is \(B=30^\circ\). Find the other two angles \(A\) and \(C\), as well as the length of side \(c\).

Remember the Law of Sines: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \]

\(\begin{aligned} A&=90^\circ \\ C&=60^\circ \\ c&=3\sqrt{3}\approx5.20 \end{aligned}\)

We can begin by using the Law of Sines to find the angle \(A\): \[\begin{aligned} \sin A&=\dfrac{a}{b}\sin B =\dfrac{6}{3}\sin30^\circ \\ &=2\left(\dfrac{1}{2}\right)=1 \\ A&=\arcsin 1=90^\circ \end{aligned}\] Then we find angle \(C\) by subtracting from \(180^\circ\): \[\begin{aligned} C&=180^\circ-A^\circ-B^\circ \\ &=180^\circ-90^\circ-30^\circ =60^\circ \end{aligned}\] Finally, we find the length of side \(c\) by again using the Law of Sines: \[\begin{aligned} c&=\dfrac{\sin C}{\sin B}\,b =\dfrac{\sin60^\circ}{\sin30^\circ}\,3 \\ &=\dfrac{\sqrt{3}}{2}\cdot\dfrac{2}{1}\cdot3 =3\sqrt{3}\approx5.20 \end{aligned}\]

aas

We check by finding \(c\) using the Law of Cosines: \[\begin{aligned} c^2&=a^2+b^2-2ab\cos C \\ &=6^2+3^2-2\cdot6\cdot3\cos60^\circ \\ &=36+9-36\cdot\dfrac{1}{2} =27 \\ c&=3\sqrt{3} \end{aligned}\] This agrees with the result found using the Law of Sines.

We could look for a second solution for \(A\): \[\begin{aligned} A_2&=180^\circ-\arcsin 1\\ &=180^\circ-90^\circ=90^\circ \end{aligned}\] However, since the angle \(A_2\) is the exact same size as the angle \(A\), there is only one triangle!
ASS: A triangle \(\triangle ABC\) has two sides of length \(a=4\,\text{cm}\) and \(b=8\,\text{cm}\). The angle opposite side \(b\) is \(B=60^\circ\). Find the other two angles \(A\) and \(C\), as well as the length of side \(c\).

Remember the Law of Sines: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \]

\(\begin{aligned} A&\approx25.66^\circ \\ C&\approx94.34^\circ \\ c&\approx9.21\,\text{cm} \end{aligned}\)

We can begin by using the Law of Sines to find the angle \(A\): \[\begin{aligned} \sin A&=\dfrac{a}{b}\sin B \\ \sin A&=\dfrac{4}{8}\sin60^\circ =\dfrac{1}{2}\left(\dfrac{\sqrt{3}}{2}\right) \\ A&=\arcsin\left(\dfrac{\sqrt{3}}{4}\right) \approx25.66^\circ \end{aligned}\] Then we find angle \(C\) by subtracting from \(180^\circ\): \[\begin{aligned} C&=180^\circ-A^\circ-B^\circ \\ C&=180^\circ-25.66^\circ-60^\circ \\ C&=94.34^\circ \end{aligned}\] Finally, we find the length of side \(c\) by again using the Law of Sines: \[\begin{aligned} c&=\dfrac{\sin C}{\sin B}b \\ c&=\dfrac{\sin94.34^\circ}{\sin60^\circ}8 \\ c&\approx9.21 \end{aligned}\]

aas

We check by finding \(c\) using the Law of Cosines: \[\begin{aligned} c^2&=a^2+b^2-2ab\cos C \\ &=4^2+8^2-2\cdot4\cdot8\cos 94.34^\circ =84.84 \\ c&=9.21 \end{aligned}\] This agrees with the result found using the Law of Sines.

When we found \(A\), there was a second solution: \[\begin{aligned} A_2&=180^\circ-\arcsin\left(\dfrac{\sqrt{3}}{4}\right) \\ &=180^\circ-25.66^\circ=154.34^\circ \end{aligned}\] Does this produce a second solution for a triangle? Let's try. If we then try to find \(C\), we get \[\begin{aligned} C_2&=180^\circ-A_2-B \\ &=180^\circ-154.34^\circ-60^\circ \\ &=-34.34^\circ \end{aligned}\] Since this is negative, there is no second triangle!

A \(13\,\text{ft}\) ladder is leaning against a wall with \(5\,\text{ft}\) of space between the base of the ladder and the wall. What are the slope and inclination of the ladder?

Notice the ladder is the hypotenuse of a right triangle.

\(\begin{aligned} m&=\dfrac{12}{5} \\ \theta&=67.38^\circ \end{aligned}\)

The ladder and the wall create a right triangle with a hypotenuse of length \(c=13\,\text{ft}\) and a base of length \(b=5\,\text{ft}\). With these values, we can find \(a\), the height of the third side: \[\begin{aligned} a^{2}&=c^{2}-b^{2} \\ &=13^{2}-5^{2} \\ &=169-25=144 \\ &=12\,\text{ft} \end{aligned}\]

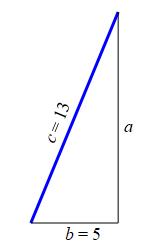
The slope is simply: \[ \text{slope}=\text{m}=\dfrac{\text{rise}}{\text{run}}=\dfrac{a}{b}=\dfrac{12}{5} \] The inclination of the ladder is the \(\arctan\) of its slope: \[\begin{aligned} \theta&=\arctan(\text{m}) \\ &=\arctan\left(\dfrac{12}{5}\right) \\ &=67.38^\circ \end{aligned}\]

aas

Review Exercises

AAS: A triangle \(\triangle ABC\) has \(2\) angles, \(A=30^\circ\) and \(B=105^\circ\), and the side opposite \(A\) has length \(a=10\,\text{in}\). Find the third angle \(C\) and the lengths of the other \(2\) sides, \(b\) and \(c\).
Try doing this without a calculator!

Remember the Law of Sines: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] And the Sum Identity for \(\sin\): \[ \sin(X+Y)=\sin X\cos Y+\cos X\sin Y \]

\(\begin{aligned} C&=45^\circ \\ b&=5(\sqrt3+1)\sqrt2\,\text{in} \\ c&=10\sqrt2\,\text{in} \end{aligned}\)

We first notice that this is an angle-angle-side (AAS) triangle, which we have not considered in detail. However, by finding the third angle, it becomes an ASA triangle, which we do know about. So, we find the value of angle \(C\) by subtracting the values of angles \(A\) and \(B\) from \(180^\circ\): \[\begin{aligned} C&=180^\circ-A-B \\ &=180^\circ-30^\circ-105^\circ =45^\circ \end{aligned}\] Next, we can use the Law of Sines to find \(b\) and \(c\): \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] This gives: (We here need the Sum Identity for \(\sin\) .) \[\begin{aligned} b&=\dfrac{a}{\sin A}\sin B=\dfrac{10}{\sin 30^\circ}\sin 105^\circ \\[5pt] &=20\sin(60^\circ+45^\circ) \\[1pt] &=20\left(\sin60^\circ\cos45^\circ+\cos60^\circ\sin45^\circ\right) \\ &=20\left(\dfrac{\sqrt3}{2}\cdot\dfrac{\sqrt2}{2}+\dfrac{1}{2}\cdot\dfrac{\sqrt2}{2}\right) \\ &=5(\sqrt3+1)\sqrt2\,\text{in} \approx 19.3 \end{aligned}\] and \[\begin{aligned} c&=\dfrac{a}{\sin A}\sin C=\dfrac{10}{\sin 30^\circ}\sin 45^\circ \\ &=10\sqrt2\,\text{in} \approx 14.1 \end{aligned}\]

aas

We check by finding \(a\) using the Law of Cosines and the values we calculated for \(b\), \(c\) and \(C\): \[\begin{aligned} a^{2}&=b^{2}+c^{2}-2bc\cos A \\ &=(5(\sqrt3+1)\sqrt2)^{2}+(10\sqrt2)^{2}-2(5(\sqrt3+1)\sqrt2\cdot10\sqrt2)\cos 30^\circ=100 \\ a&=10 \end{aligned}\] This agrees with the description of the problem which states that \(a=10 \text{in}\).
AAA: Given a triangle with angles \(D=45^\circ\), \(E=60^\circ\) and \(F=75^\circ\), find at least two sets of side lengths \(d\), \(e\) and \(f\) which form a valid triangle.

Remember the Law of Sines: \[ \dfrac{\sin(D)}{d}=\dfrac{\sin(E)}{e}=\dfrac{\sin(F)}{f} \] Also, notice that \(75^\circ=45^\circ+30^\circ\). Use the Sum of Angles identity.

For any choice of \(d\), there is a solution: \[ e=\dfrac{\sqrt3}{\sqrt2}d \qquad f=\dfrac{\sqrt3+1}{2}d \] For example, here are three solutions. \[\begin{aligned} d&=1 \qquad& e&=\dfrac{\sqrt3}{\sqrt2} \qquad& f&=\dfrac{\sqrt3+1}{2} \\ d&=2 \qquad& e&=\sqrt6 \qquad& f&=\sqrt3+1 \\ d&=\sqrt2 \qquad& e&=\sqrt3 \qquad& f&=\dfrac{\sqrt3+1}{\sqrt2} \\ \end{aligned}\]

We first find the \(\sin\) of angles \(D=45^\circ\) and \(E=60^\circ\), which we know from standard right triangles. \[\begin{aligned} \sin D=\sin 45^\circ=\dfrac{\sqrt{2} }{2} \\ \sin E=\sin 60^\circ=\dfrac{\sqrt{3} }{2} \end{aligned}\] Next, we need to find the sin of angle \(F=75^\circ\). There is no easy way to remember this. However, since \(75^\circ=45^\circ+30^\circ\), we can use the Sum Identity for Sine: \[\begin{aligned} \sin(A+B)&=\sin(A)\cos(B)+\cos(A)\sin(B) \\ \sin(45^\circ+30^\circ)&=(\sin45^\circ)(\cos30^\circ)+(\cos45^\circ)(\sin30^\circ) \\ \sin75^\circ&=\left(\dfrac{\sqrt{2} }{2}\right)\left(\dfrac{\sqrt{3} }{2}\right)+\left(\dfrac{\sqrt{2} }{2}\right)\left(\dfrac{1}{2}\right) \\ \sin F&=\dfrac{\sqrt{2} }{4}(\sqrt{3}+1) \end{aligned}\] Now we know the \(\sin\) of all \(3\) angles. We can now use the Law of Sines to calculate the ratio between the sines that will allow us find two different sets of side lengths that would both be valid given the \(3\) angles: \[\begin{aligned} \dfrac{\sin(D)}{d}&=\dfrac{\sin(E)}{e}=\dfrac{\sin(F)}{f} \\ \dfrac{\sin(45^\circ)}{d}&=\dfrac{\sin(60^\circ)}{e}=\dfrac{\sin(75^\circ)}{f} \\ \dfrac{\;\;\dfrac{\sqrt{2} }{2}\;\;}{d}&=\dfrac{\;\;\dfrac{\sqrt{3} }{2}\;\;}{e}=\dfrac{\dfrac{\sqrt{2} }{4}(\sqrt{3}+1)}{f} \end{aligned}\] This allows us to express \(e\) and \(f\) in terms of \(d\): \[ e=\dfrac{\sqrt3}{\sqrt2}d \qquad f=\dfrac{\sqrt3+1}{2}d \] For each choice of \(d\), we get another solution for the sides. For example, here are three solutions. \[\begin{aligned} d&=1 \qquad& e&=\dfrac{\sqrt3}{\sqrt2} \qquad& f&=\dfrac{\sqrt3+1}{2} \\ d&=2 \qquad& e&=\sqrt6 \qquad& f&=\sqrt3+1 \\ d&=\sqrt2 \qquad& e&=\sqrt3 \qquad& f&=\dfrac{\sqrt3+1}{\sqrt2} \\ \end{aligned}\]

aas

1. Trigonometry

Exercises

a. Angular Measure

b. Triangle Definitions

c. Circle Definitions

d. Trig Identities

e. Inverse Trig Functions

f. Applications

Review Exercises

Heading