3. Trigonometry

b. Triangle Definitions

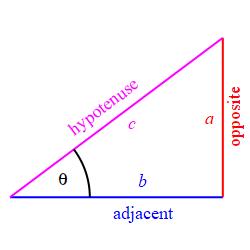
In the right triangle at the right, the angle at the base has been denoted by \(\theta\), the opposite side is the altitude \(a\), the adjacent side is the base \(b\) and the hypotenuse is the diagonal side \(c\). In terms of these the six trig functions Sine  Cosine Tangent  Cotangent Secant  Cosecant are defined to be: \[\begin{aligned} \sin\theta&=\dfrac{\text{Opp}}{\text{Hyp}}=\dfrac{a}{c}\quad &\cos\theta&=\dfrac{\text{Adj}}{\text{Hyp}}=\dfrac{b}{c} \\[8pt] \tan\theta&=\dfrac{\text{Opp}}{\text{Adj}}=\dfrac{a}{b}\quad &\cot\theta&=\dfrac{\text{Adj}}{\text{Opp}}=\dfrac{b}{a} \\[8pt] \sec\theta&=\dfrac{\text{Hyp}}{\text{Adj}}=\dfrac{c}{b}\quad &\csc\theta&=\dfrac{\text{Hyp}}{\text{Opp}}=\dfrac{c}{a} \end{aligned}\]

Memorize this!

The figure shows a right triangle with legs on the bottom and right. The angle at the bottom left is labeled theta. The bottom side is labeled adjacent and b. The right side is labeled opposite and a. The third side is labeled hypotenuse and c.

There is a Mnemonic to remember the first three of these:

Mnemonic: SOH CAH TOA which stands for Sin=Opp/Hyp   Cos=Adj/Hyp   Tan=Opp/Adj

Based on these we have the standard quotient and reciprocal identities:

\[\begin{aligned} \tan\theta&=\dfrac{\sin\theta}{\cos\theta}\quad &\cot\theta&=\dfrac{\cos\theta}{\sin\theta}=\dfrac{1}{\tan\theta} \\[8pt] \sec\theta&=\dfrac{1}{\cos\theta}\quad &\csc\theta&=\dfrac{1}{\sin\theta} \end{aligned}\]

Given the right triangle shown with adjacent side \(5\) and opposite side \(12\), find the hypotenuse and the six trig functions for the angle \(\theta\).

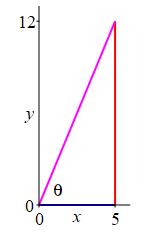
eg_5-12-13

By the Pythagorean Theorem, the hypotenuse is \(\text{Hyp}\,=\sqrt{5^2+12^2}=\sqrt{169}=13\). So, the six trig functions are: \[\begin{aligned} \sin\theta&=\dfrac{\text{Opp}}{\text{Hyp}}=\dfrac{12}{13}\quad &\cos\theta&=\dfrac{\text{Adj}}{\text{Hyp}}=\dfrac{5}{13} \\[8pt] \tan\theta&=\dfrac{\text{Opp}}{\text{Adj}}=\dfrac{12}{5}\quad &\cot\theta&=\dfrac{\text{Adj}}{\text{Opp}}=\dfrac{5}{12} \\[8pt] \sec\theta&=\dfrac{\text{Hyp}}{\text{Adj}}=\dfrac{13}{5}\quad &\csc\theta&=\dfrac{\text{Hyp}}{\text{Opp}}=\dfrac{13}{12} \end{aligned}\]

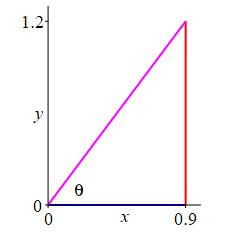
Given the right triangle shown with adjacent side \(0.9\) and opposite side \(1.2\), find the hypotenuse and the six trig functions for the angle \(\theta\).

ex_9-12-15

\(\begin{aligned} \sin\theta&=\dfrac{4}{5}\quad &\cos\theta&=\dfrac{3}{5} \\ \tan\theta&=\dfrac{4}{3}\quad &\cot\theta&=\dfrac{3}{4} \\ \sec\theta&=\dfrac{5}{3}\quad &\csc\theta&=\dfrac{5}{4} \end{aligned}\)

By the Pythagorean Theorem, the hypotenuse is \(\text{Hyp}\,=\sqrt{.9^2+1.2^2}=\sqrt{.81+1.44}=\sqrt{2.25}=1.5\). So, the six trig functions are: \[\begin{aligned} \sin\theta&=\dfrac{\text{Opp}}{\text{Hyp}}=\dfrac{1.2}{1.5}=\dfrac{4}{5}\quad &\cos\theta&=\dfrac{\text{Adj}}{\text{Hyp}}=\dfrac{0.9}{1.5}=\dfrac{3}{5} \\[8pt] \tan\theta&=\dfrac{\text{Opp}}{\text{Adj}}=\dfrac{1.2}{0.9}=\dfrac{4}{3}\quad &\cot\theta&=\dfrac{\text{Adj}}{\text{Opp}}=\dfrac{0.9}{1.2}=\dfrac{3}{4} \\[8pt] \sec\theta&=\dfrac{\text{Hyp}}{\text{Adj}}=\dfrac{1.5}{0.9}=\dfrac{5}{3}\quad &\csc\theta&=\dfrac{\text{Hyp}}{\text{Opp}}=\dfrac{1.5}{1.2}=\dfrac{5}{4} \end{aligned}\]

cj  

© MYMathApps

Supported in part by NSF Grant #1123255