3. Trigonometry
c. Circle Definitions
Recall: \[\begin{aligned} \sin\theta&=\dfrac{y}{r}\quad &\tan\theta&=\dfrac{y}{x}\quad &\sec\theta&=\dfrac{r}{x} \\[8pt] \cos\theta&=\dfrac{x}{r}\quad &\cot\theta&=\dfrac{x}{y}\quad &\csc\theta&=\dfrac{r}{y} \end{aligned}\]
3. Unit Circle
Now that we know how to find the trig functions using the circle definitions, we want to understand what this says when the circle is a unit circle, i.e. a circle of radius \(1\).
The fact that the radius is \(1\) allows us to write the trig functions as follows: \[\begin{aligned} \sin\theta&=y\quad &\tan\theta&=\dfrac{y}{x}\quad &\sec\theta&=\dfrac{1}{x} \\[8pt] \cos\theta&=x\quad &\cot\theta&=\dfrac{x}{y}\quad &\csc\theta&=\dfrac{1}{y} \end{aligned}\]
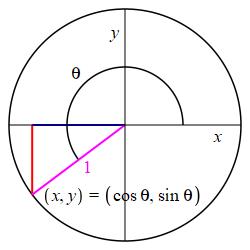
In particular:
If a point on the unit circle has coordinates \((x,y)\) then: \[ \sin\theta=y \qquad \text{and} \qquad \cos\theta=x \] Conversely, the point on the unit circle at angle \(\theta\) is: \[ (x,y)=(\cos\theta,\sin\theta) \]
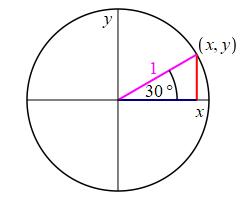
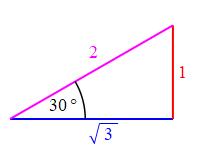
As an example, let's find the coordinates of a point on the unit circle at an angle of \(30^\circ\) from the \(x\)-axis. We know the coordinates are \((x,y)=(\cos30^\circ,\sin30^\circ)\). To find \(\sin\) and \(\cos\), we look at the \(30^\circ - 60^\circ - 90^\circ\) triangle with sides \(1, 2, \sqrt{3}\). So \[ \sin30^\circ=\dfrac{1}{2} \quad \text{and} \quad \cos30^\circ=\dfrac{\sqrt{3}}{2} \] So the coordinates of the point are: \[ (x,y)=\left(\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right) \]
Using the unit circle, find the \(\sin135^\circ\) and \(\cos135^\circ\).
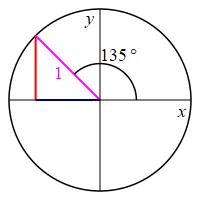
How are \(\sin135^\circ\) and \(\cos135^\circ\) related to \(\sin45^\circ\) and \(\cos45^\circ\)?
\(\begin{aligned} \sin135^\circ&=\dfrac{\sqrt{2}}{2} \\ \cos135^\circ&=-\,\dfrac{\sqrt{2}}{2} \end{aligned}\)
Look at the point on the unit circle at \(135^\circ\): \[ (x,y)=(\cos135^\circ,\sin135^\circ) \] The coordinates are the same as those at \(45^\circ\): \[ (x,y)=(\cos45^\circ,\sin45^\circ) =\left(\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\right) \] except there needs to be a minus on the \(x\) component. So \[ (x,y)=(\cos135^\circ,\sin135^\circ) =\left(-\,\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\right) \]
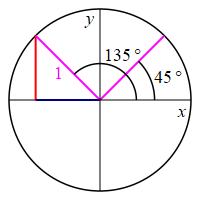
We conclude: \[ \sin135^\circ=\dfrac{\sqrt{2}}{2} \quad \text{and} \quad \cos135^\circ=-\,\dfrac{\sqrt{2}}{2} \]
aas
Consider a unit circle and the ray at the angle \(\theta\) which passes through the point \((0.8,-0.6)\), identify the six trig functions for the angle \(\theta\).
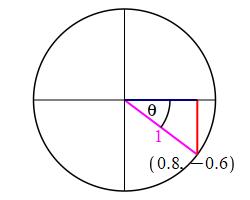
\(\begin{aligned} \sin\theta&=-\,\dfrac{3}{5}\quad &\tan\theta&=-\,\dfrac{3}{4}\quad &\sec\theta&=\dfrac{5}{4} \\ \cos\theta&=\dfrac{4}{5}\quad &\cot\theta&=-\,\dfrac{4}{3}\quad &\csc\theta&=-\,\dfrac{5}{3} \end{aligned}\)
Given that this is a unit circle, we know that it has a radius of \(r=1\), and we are given that the ray passes through the point \((x,y)=(0.8,-0.6)\). Therefore, the trig functions are: \[\begin{aligned} \sin\theta&=\dfrac{y}{r}=\dfrac{-0.6}{1}=-\,\dfrac{3}{5}\quad &\cos\theta&=\dfrac{x}{r}=\dfrac{0.8}{1}=\dfrac{4}{5} \\[8pt] \tan\theta&=\dfrac{y}{x}=\dfrac{-0.6}{0.8}=-\,\dfrac{3}{4}\quad &\cot\theta&=\dfrac{x}{y}=\dfrac{0.8}{-0.6}=-\,\dfrac{4}{3} \\[8pt] \sec\theta&=\dfrac{r}{x}=\dfrac{1}{0.8}=\dfrac{5}{4}\quad &\csc\theta&=\dfrac{r}{y}=\dfrac{1}{-0.6}=-\,\dfrac{5}{3} \end{aligned}\]
cj
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum