3. Trigonometry

d. Trig Identities

2. Parity, Complementarity and Supplementarity Identities

Parity Identities

Parity Identities: Sine and Cosine
Sine is an odd function and cosine is an even function: sin⁡(−θ)=−sin⁡(θ)cos⁡(−θ)=cos⁡(θ) \sin(-\theta)=-\sin(\theta) \qquad \cos(-\theta)=\cos(\theta) ⇐⇐\Leftarrow\Leftarrow Read it! It simply explains the plot.

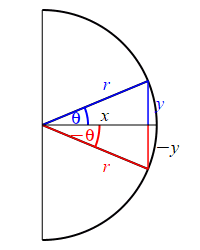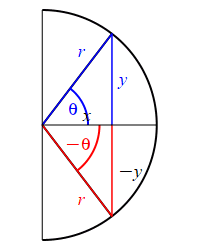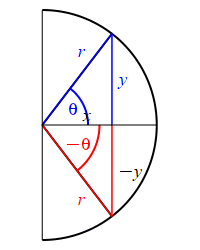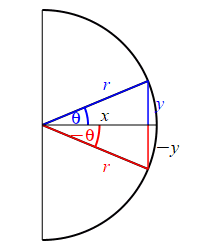
prop_parity_anim
Parity

Proof

Looking at the figure, the ray at the angle θ\theta hits the circle at the point (x,y)(x,y), while the ray at the angle −θ-\theta hits the circle at the point (x,−y)(x,-y). So: sin⁡(θ)=yrwhilesin⁡(−θ)=−yr=−sin⁡(θ) \sin(\theta)=\dfrac{y}{r} \quad \text{while} \quad \sin(-\theta)=\dfrac{-y}{r}=-\sin(\theta) and cos⁡(θ)=xrwhilecos⁡(−θ)=xr=cos⁡(θ) \cos(\theta)=\dfrac{x}{r} \quad \text{while} \quad \cos(-\theta)=\dfrac{x}{r}=\cos(\theta)

[×]

The parity of sin⁡\sin and cos⁡\cos can also be understood by looking at their plots.

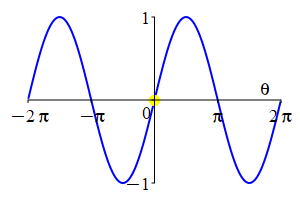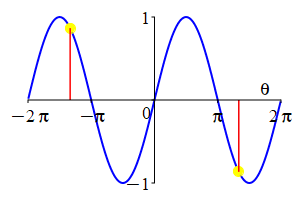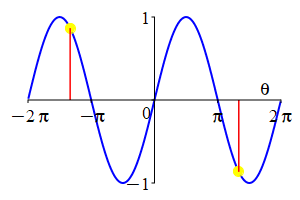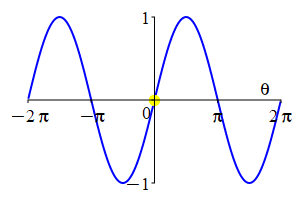
prop_parity_sin_anim
sin⁡(−θ)=−sin⁡(θ)\sin(-\theta)=-\sin(\theta)
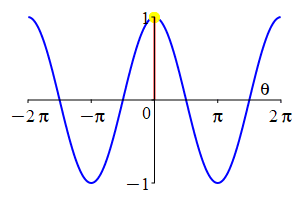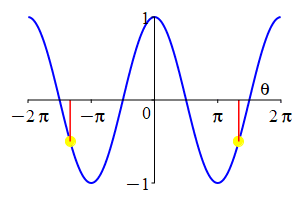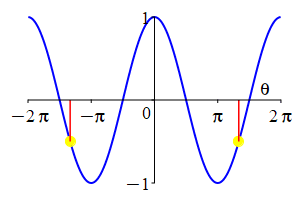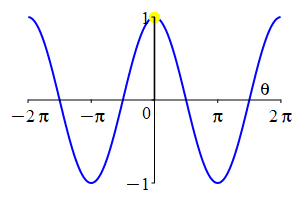
prop_parity_cos_anim
cos⁡(−θ)=cos⁡(θ)\cos(-\theta)=\cos(\theta)

As a consequence:

Parity Identities: Tangent, Cotangent, Secant and Cosecant
Tangent, cotangent and cosecant are odd functions and secant is an even function: tan⁡(−θ)=−tan⁡(θ)cot⁡(−θ)=−cot⁡(θ) \tan(-\theta)=-\tan(\theta) \qquad \cot(-\theta)=-\cot(\theta) sec⁡(−θ)=sec⁡(θ)csc⁡(−θ)=−csc⁡(θ) \sec(-\theta)=\sec(\theta) \qquad \quad \csc(-\theta)=-\csc(\theta) ⇐⇐\Leftarrow\Leftarrow It's a simple computation.

Proof

tan⁡(−θ)=sin⁡(−θ)cos⁡(−θ)=−sin⁡(θ)cos⁡(θ)=−tan⁡(θ) \tan(-\theta)=\dfrac{\sin(-\theta)}{\cos(-\theta)} =\dfrac{-\sin(\theta)}{\cos(\theta)}=-\tan(\theta) cot⁡(−θ)=cos⁡(−θ)sin⁡(−θ)=cos⁡(θ)−sin⁡(θ)=−cot⁡(θ) \cot(-\theta)=\dfrac{\cos(-\theta)}{\sin(-\theta)} =\dfrac{\cos(\theta)}{-\sin(\theta)}=-\cot(\theta) sec⁡(−θ)=1cos⁡(−θ)=1cos⁡(θ)=sec⁡(θ) \sec(-\theta)=\dfrac{1}{\cos(-\theta)} =\dfrac{1}{\cos(\theta)}=\sec(\theta) \qquad csc⁡(−θ)=1sin⁡(−θ)=1−sin⁡(θ)=−csc⁡(θ) \csc(-\theta)=\dfrac{1}{\sin(-\theta)} =\dfrac{1}{-\sin(\theta)}=-\csc(\theta)

[×]

Complementarity Identities

Complementarity Identities: Sine and Cosine
The complementary angle for θ\theta is 90∘−θ90^\circ-\theta or π2−θ\dfrac{\pi}{2}-\theta. sin⁡(π2−θ)=cos⁡(θ)cos⁡(π2−θ)=sin⁡(θ) \sin\left(\dfrac{\pi}{2}-\theta\right)=\cos(\theta) \qquad \cos\left(\dfrac{\pi}{2}-\theta\right)=\sin(\theta) ⇐⇐\Leftarrow\Leftarrow Read it! It simply explains the plot.

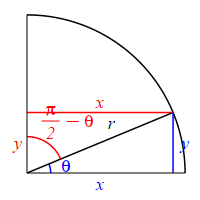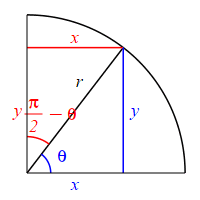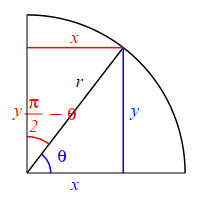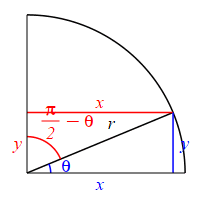
prop_comp_anim

Proof

Looking at the figure, if the angle θ\theta is measured counterclockwise from the positive xx-axis, then the complementary angle π2−θ\dfrac{\pi}{2}-\theta can be measured clockwise from the positive yy-axis. So switching from an angle to its complement is equivalent to a reflection through the 45∘45^\circ diagonal line. This means that the roles of xx and yy are interchanged. (The opposite and adjacent sides are interchanged.) So: sin⁡(π2−θ)=OppHyp=xrcos⁡(θ)=AdjHyp=xr\begin{aligned} \sin\left(\dfrac{\pi}{2}-\theta\right) &=\dfrac{\text{Opp}}{\text{Hyp}} =\dfrac{x}{r} \\ \cos(\theta) &=\dfrac{\text{Adj}}{\text{Hyp}} =\dfrac{x}{r} \end{aligned} and cos⁡(π2−θ)=AdjHyp=yrsin⁡(θ)=OppHyp=yr\begin{aligned} \cos\left(\dfrac{\pi}{2}-\theta\right) &=\dfrac{\text{Adj}}{\text{Hyp}} =\dfrac{y}{r} \\ \sin(\theta) &=\dfrac{\text{Opp}}{\text{Hyp}} =\dfrac{y}{r} \end{aligned}

[×]

The complementarity identities can also be understood by comparing the plot of sin⁡(θ)\sin(\theta) with that of cos⁡(π2−θ)\cos\left(\dfrac{\pi}{2}-\theta\right) and the plot of cos⁡(θ)\cos(\theta) with that of sin⁡(π2−θ)\sin\left(\dfrac{\pi}{2}-\theta\right).

prop_parity_sin_anim
sin⁡(θ)\sin(\theta)
prop_parity_cos_anim
cos⁡(θ)\cos(\theta)
prop_parity_sin_anim
cos⁡(π2−θ)\cos\left(\dfrac{\pi}{2}-\theta\right)
prop_parity_cos_anim
sin⁡(π2−θ)\sin\left(\dfrac{\pi}{2}-\theta\right)

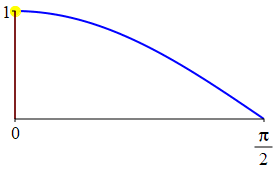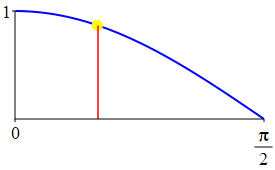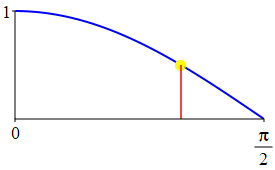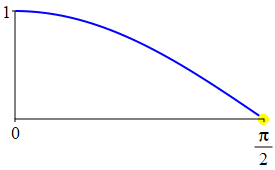
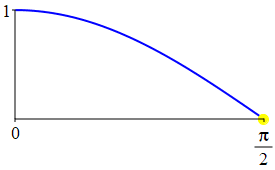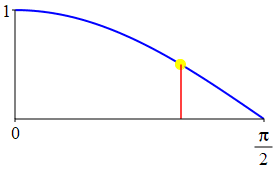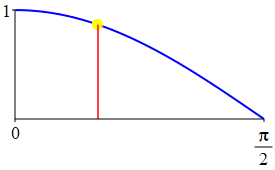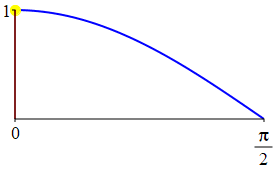
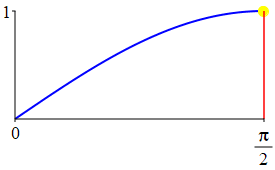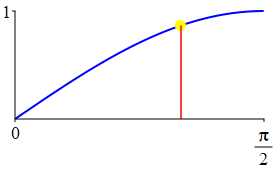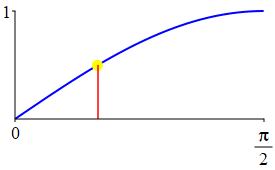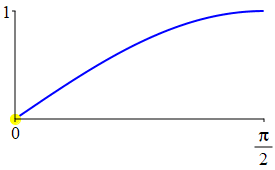
As a consequence:

Complementarity Identities: Tangent, Cotangent, Secant and Cosecant
tan⁡(π2−θ)=cot⁡(θ)cot⁡(π2−θ)=tan⁡(θ) \tan\left(\dfrac{\pi}{2}-\theta\right)=\cot(\theta) \qquad \cot\left(\dfrac{\pi}{2}-\theta\right)=\tan(\theta) sec⁡(π2−θ)=csc⁡(θ)csc⁡(π2−θ)=sec⁡(θ) \sec\left(\dfrac{\pi}{2}-\theta\right)=\csc(\theta) \qquad \csc\left(\dfrac{\pi}{2}-\theta\right)=\sec(\theta) ⇐⇐\Leftarrow\Leftarrow It's a simple computation.

Proof

tan⁡(π2−θ)=sin⁡(π2−θ)cos⁡(π2−θ)=cos⁡(θ)sin⁡(θ)=cot⁡(θ) \tan\left(\dfrac{\pi}{2}-\theta\right) =\dfrac{\sin\left(\dfrac{\pi}{2}-\theta\right)}{\cos\left(\dfrac{\pi}{2}-\theta\right)} =\dfrac{\cos(\theta)}{\sin(\theta)}=\cot(\theta) cot⁡(π2−θ)=cos⁡(π2−θ)sin⁡(π2−θ)=sin⁡(θ)cos⁡(θ)=tan⁡(θ) \cot\left(\dfrac{\pi}{2}-\theta\right) =\dfrac{\cos\left(\dfrac{\pi}{2}-\theta\right)}{\sin\left(\dfrac{\pi}{2}-\theta\right)} =\dfrac{\sin(\theta)}{\cos(\theta)}=\tan(\theta) sec⁡(π2−θ)=1cos⁡(π2−θ)=1sin⁡(θ)=csc⁡(θ) \sec\left(\dfrac{\pi}{2}-\theta\right) =\dfrac{1}{\cos\left(\dfrac{\pi}{2}-\theta\right)} =\dfrac{1}{\sin(\theta)}=\csc(\theta) csc⁡(π2−θ)=1sin⁡(π2−θ)=1cos⁡(θ)=sec⁡(θ) \csc\left(\dfrac{\pi}{2}-\theta\right) =\dfrac{1}{\sin\left(\dfrac{\pi}{2}-\theta\right)} =\dfrac{1}{\cos(\theta)}=\sec(\theta)

[×]

Notice that switching from an angle to its complementary angle interchanges each trig function with its complementary function: sin⁡\sin with cos⁡\cos, tan⁡\tan with cot⁡\cot, sec⁡\sec with csc⁡\csc. This is, in fact, why they are called “co”-functions.

Supplementarity Identities

Supplementarity Identities: Sine and Cosine
The supplementary angle for θ\theta is 180∘−θ180^\circ-\theta or π−θ\pi-\theta. sin⁡(π−θ)=sin⁡(θ)cos⁡(π−θ)=−cos⁡(θ) \sin(\pi-\theta)=\sin(\theta) \qquad \cos(\pi-\theta)=-\cos(\theta) ⇐⇐\Leftarrow\Leftarrow Read it! It simply explains the plot.

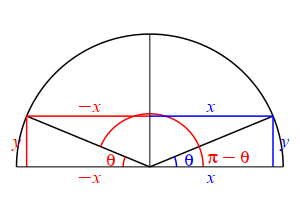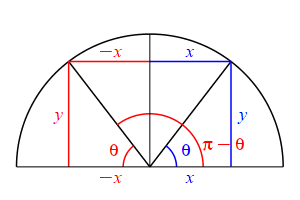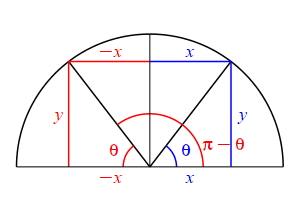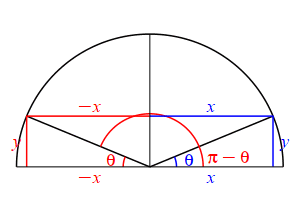
prop_supp_anim

Proof

Looking at the figure, the ray at the angle θ\theta hits the circle at the point (x,y)(x,y), while the ray at the angle π−θ\pi-\theta hits the circle at the point (−x,y)(-x,y). So: sin⁡(θ)=yrwhilesin⁡(π−θ)=yr=sin⁡(θ) \sin(\theta)=\dfrac{y}{r} \quad \text{while} \quad \sin(\pi-\theta)=\dfrac{y}{r}=\sin(\theta) and cos⁡(θ)=xrwhilecos⁡(π−θ)=−xr=−cos⁡(θ) \cos(\theta)=\dfrac{x}{r} \quad \text{while} \quad \cos(\pi-\theta)=\dfrac{-x}{r}=-\cos(\theta)

[×]

The supplementarity identities can also be understood by comparing the plot of sin⁡(θ)\sin(\theta) with that of sin⁡(π−θ)\sin(\pi-\theta) and the plot of cos⁡(θ)\cos(\theta) with that of cos⁡(π−θ)\cos(\pi-\theta).

prop_supp_sin_anim
sin⁡(θ)=sin⁡(π−θ)\sin(\theta)=\sin(\pi-\theta).
prop_supp_cos_anim
cos⁡(θ)=−cos⁡(π−θ)\cos(\theta)=-\cos(\pi-\theta).

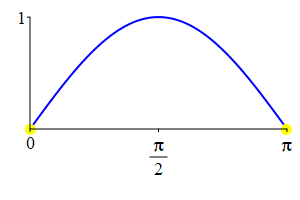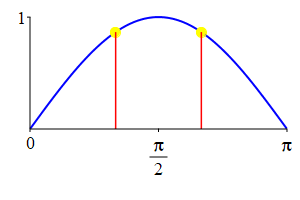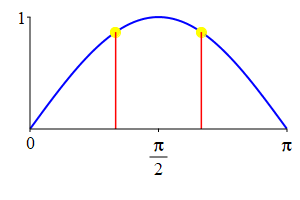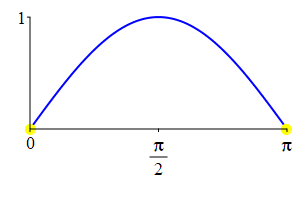
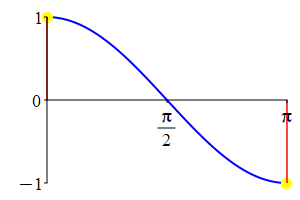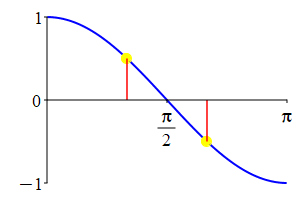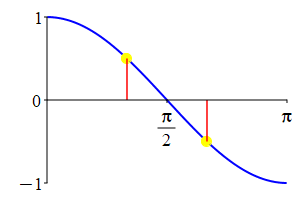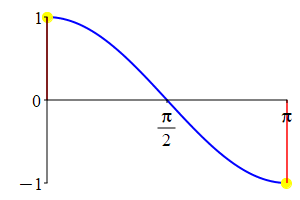
As a consequence:

Supplementarity Identities: Tangent, Cotangent, Secant and Cosecant
tan⁡(π−θ)=−tan⁡(θ)cot⁡(π−θ)=−cot⁡(θ) \tan(\pi-\theta)=-\tan(\theta) \qquad \cot(\pi-\theta)=-\cot(\theta) sec⁡(π−θ)=−sec⁡(θ)csc⁡(π−θ)=csc⁡(θ) \sec(\pi-\theta)=-\sec(\theta) \qquad \csc(\pi-\theta)=\csc(\theta) \quad ⇐⇐\Leftarrow\Leftarrow It's a simple computation.

Proof

tan⁡(π−θ)=sin⁡(π−θ)cos⁡(π−θ)=sin⁡(θ)−cos⁡(θ)=−tan⁡(θ) \tan(\pi-\theta)=\dfrac{\sin(\pi-\theta)}{\cos(\pi-\theta)} =\dfrac{\sin(\theta)}{-\cos(\theta)}=-\tan(\theta) cot⁡(π−θ)=cos⁡(π−θ)sin⁡(π−θ)=−cos⁡(θ)sin⁡(θ)=−cot⁡(θ) \cot(\pi-\theta)=\dfrac{\cos(\pi-\theta)}{\sin(\pi-\theta)} =\dfrac{-\cos(\theta)}{\sin(\theta)}=-\cot(\theta) sec⁡(π−θ)=1cos⁡(π−θ)=1−cos⁡(θ)=−sec⁡(θ) \sec(\pi-\theta)=\dfrac{1}{\cos(\pi-\theta)} =\dfrac{1}{-\cos(\theta)}=-\sec(\theta) csc⁡(π−θ)=1sin⁡(π−θ)=1sin⁡(θ)=csc⁡(θ) \csc(\pi-\theta)=\dfrac{1}{\sin(\pi-\theta)} =\dfrac{1}{\sin(\theta)}=\csc(\theta) \qquad

[×]

Given that sin⁡60∘=32andcos⁡60∘=12 \sin60^\circ=\dfrac{\sqrt{3}}{2} \quad \text{and} \quad \cos60^\circ=\dfrac{1}{2} find sin⁡(−30∘)\sin(-30^\circ) and cos⁡(−30∘)\cos(-30^\circ).

We use both the parity and complementarity identities for sin⁡(θ)\sin(\theta) and cos⁡(θ)\cos(\theta).
Applying the parity identity and then the complementarity, we see: sin⁡(−30∘)=−sin⁡(30∘)=−cos⁡(60∘)=−12 \sin(-30^\circ) = -\sin(30^\circ)=-\cos(60^\circ)=-\dfrac{1}{2} Similarly: cos⁡(−30∘)=cos⁡(30∘)=sin⁡(60∘)=32 \cos(-30^\circ)=\cos(30^\circ)=\sin(60^\circ)=\dfrac{\sqrt{3}}{2}

Given that sin⁡60∘=32andcos⁡60∘=12 \sin60^\circ=\dfrac{\sqrt{3}}{2} \quad \text{and} \quad \cos60^\circ=\dfrac{1}{2} find sin⁡(−150∘)\sin(-150^\circ).

Hint

Go from −150∘-150^\circ to 150∘150^\circ to 30∘30^\circ to 60∘60^\circ.

[×]

Answer

sin⁡(−150∘)=−12\sin(-150^\circ) = -\dfrac{1}{2}

[×]

Solution

We applying the parity identity for sin⁡\sin, then the supplementarity identity for sin⁡\sin and finally the complementarity identity: sin⁡(−150∘)=−sin⁡(150∘)=−sin⁡(30∘)=−cos⁡(60∘)=−12 \sin(-150^\circ)=-\sin(150^\circ)=-\sin(30^\circ) =-\cos(60^\circ)=-\dfrac{1}{2}

[×]

© 2025 MYMathApps

Supported in part by NSF Grant #1123255