3. Trigonometry
e. Inverse Trig Functions
3. Inverse Tangent & Cotangent
Arc Tangent
The tangent function is not one-to-one, since for example \[ \tan(\theta+\pi)=\tan(\theta) \] We pick the branch with \(-\,\dfrac{\pi}{2} \lt \theta \lt \dfrac{\pi}{2}\).
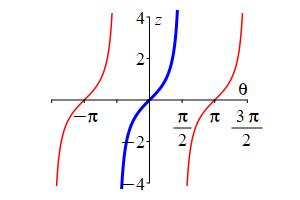
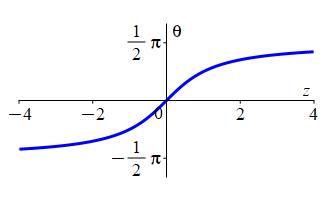
The inverse function of \(\tan\) is \(\arctan\) (read “arc tangent”) or \(\tan^{-1}\) (read “inverse tangent”) which satisfies \[ \arctan(z)=\theta \qquad \text{where} \qquad z=\tan(\theta) \] provided \(-\,\dfrac{\pi}{2} \lt \theta \lt \dfrac{\pi}{2}\).
Notice that \(-\,\dfrac{\pi}{2} \le \theta \le \dfrac{\pi}{2}\) is quadrants IV and I only.
Compute each of the following.
-
\(\arctan\dfrac{1}{\sqrt{3}}\)
\(\arctan\dfrac{1}{\sqrt{3}}=\dfrac{\pi}{6}\)
-
\(\arctan(-\sqrt{3})\)
\(\arctan(-\sqrt{3})=-\,\dfrac{\pi}{3}\)
-
\(\arctan(-1)\)
\(\arctan(-1)=-\,\dfrac{\pi}{4}\)
Arc Cotangent
The cotangent function is not one-to-one, since for example \[ \cot(\theta+\pi)=\cot(\theta) \] We pick the branch with \(0 \lt \theta \lt \pi\).
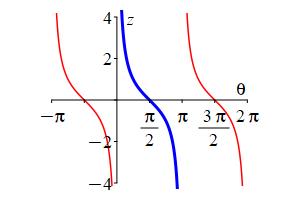
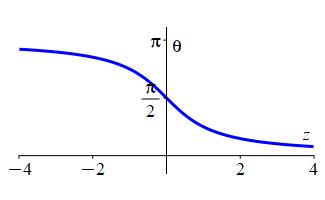
The inverse function of \(\cot\) is \(\text{arccot}\) (read “arc cotangent”) or \(\cot^{-1}\) (read “inverse cotangent”) which satisfies \[ \text{arccot}(z)=\theta \qquad \text{where} \qquad z=\cot(\theta) \] provided \(0 \lt \theta \lt \pi\).
Notice that \(0 \le \theta \le \pi\) is quadrants I and II only.
Compute each of the following.
-
\(\text{arccot}\,\dfrac{1}{\sqrt{3}}\)
\(\text{arccot}\,\dfrac{1}{\sqrt{3}}=\dfrac{\pi}{3}\)
-
\(\text{arccot}(-\sqrt{3})\)
\(\text{arccot}(-\sqrt{3})=\dfrac{5\pi}{6}\)
If you answered \(-\,\dfrac{\pi}{6}\), you are correct that \(\cot\dfrac{-\pi}{6}=-\sqrt{3}\), but you have the wrong quadrant. \(\text{arccot}(z)\) always returns a value in the \(1^\text{st}\) or \(2^\text{nd}\) quadrant. \(-\,\dfrac{\pi}{6}\) is in the \(4^\text{th}\) quadrant.
-
\(\text{arccot}(-1)\)
\(\text{arccot}(-1)=\dfrac{3\pi}{4}\)
If you answered \(-\,\dfrac{\pi}{4}\), you are correct that \(\cot\dfrac{-\pi}{4}=-1\), but you have the wrong quadrant. \(\text{arccot}(z)\) always returns a value in the \(1^\text{st}\) or \(2^\text{nd}\) quadrant. \(-\,\dfrac{\pi}{6}\) is in the \(4^\text{th}\) quadrant.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum