11. Stokes' Theorem

Stokes' Theorem
Let SS be a nice surface in R3\mathbf{R}^3 with a nice properly oriented boundary, ∂S\partial S, and let F⃗\vec{F} be a nice vector field on SS. Then ∬S∇⃗×F⃗⋅dS⃗=∮∂SF⃗⋅ds⃗ \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} =\oint_{\partial S} \vec{F}\cdot d\vec{s} as seen from the tip of the normal vector to the surface.

Exercises

    a. The Theorem

  1. Find ∬S∇⃗×F⃗⋅dS⃗\displaystyle \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} for F⃗=⟨−2y,2x,xy⟩\vec{F}=\langle-2y,2x,xy\rangle over the surface of the part of the sphere x2+y2+z2=17x^2+y^2+z^2=17 above z=1z=1 oriented upward, using Stokes' Theorem.

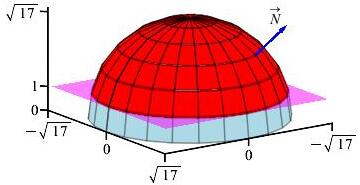
    x_sph_cap

    Hint

    What is the boundary curve?

    [×]

    Answer

    ∮∂SF⃗⋅ds⃗=64π\displaystyle \oint_{\partial S} \vec{F}\cdot d\vec{s}=64\pi

    [×]

    Solution

    By Stokes' Theorem, ∬S∇⃗×F⃗⋅dS⃗=∮∂SF⃗⋅ds⃗\displaystyle \iint_{S} \vec{\nabla}\times \vec{F}\cdot d\vec{S} =\oint_{\partial S} \vec{F}\cdot d\vec{s}. So we parameterize the boundary curve at z=1z=1 and evaluate F⃗\vec{F} on that curve. At z=1z=1, x2+y2=16x^{2}+y^{2}=16. So r2=16r=4\begin{aligned} r^{2}&=16\\ r&=4 \end{aligned} We can then parametrize our curve as: r⃗(θ)=⟨4cos⁡θ,4sin⁡θ,1⟩ \vec{r}(\theta) =\langle 4\cos\theta,4\sin\theta,1\rangle and compute the velocity: v⃗(θ)=⟨−4sin⁡θ,4cos⁡θ,0⟩ \vec{v}(\theta) =\left\langle -4\sin\theta,4\cos\theta,0\right\rangle Since the normal is upward, the boundary must be oriented counterclockwise. This velocity is counterclockwise. Our parametrized vector field, F⃗=⟨−2y,2x,xy⟩\vec{F}=\langle -2y,2x,xy\rangle, is then: F⃗∣r⃗(θ)=⟨−8sin⁡θ,8cos⁡θ,16sin⁡θcos⁡θ⟩ \left.\vec{F}\right|_{\vec{r}(\theta)} =\langle -8\sin\theta,8\cos\theta,16\sin\theta\cos\theta\rangle We evaluate the line integral as: ∮∂SF⃗⋅ds⃗=∫02π⟨−8sin⁡θ,8sin⁡2θ,16sin⁡θcos⁡θ⟩⋅⟨−4sin⁡θ,4cos⁡θ,0⟩dθ=∫02π(32sin⁡2θ+32cos⁡2θ)dθ=∫02π32dθ=64π\begin{aligned} \oint_{\partial S}\vec{F}\cdot d\vec{s} &=\int_{0}^{2\pi} \langle -8\sin\theta,8\sin^{2}\theta,16\sin\theta\cos\theta\rangle \cdot\langle -4\sin\theta,4\cos\theta,0\rangle\,d\theta \\ &=\int_{0}^{2\pi}(32\sin^{2}\theta+32\cos^{2}\theta)\,d\theta =\int_{0}^{2\pi}32\,d\theta= 64\pi \end{aligned}

    [×]

  2. Compute ∬S∇⃗×F⃗⋅dS⃗\displaystyle \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} for the vector field F⃗=⟨−yz,xz,xyz⟩\vec{F}=\langle-yz,xz,xyz\rangle over the quartic surface SS given by z=(x2+y2)2z=(x^2+y^2)^2 for z≤16z \le 16, oriented down and out.

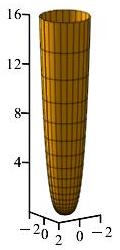
    x_quartic_parab

    Hint

    What is the radius of the boundary circle?

    [×]

    Answer

    ∬S∇⃗×F⃗⋅dS⃗=∮∂SF⃗⋅ds⃗=−128π\displaystyle \iint_{S} \vec{\nabla}\times\vec{F}\cdot d\vec{S} =\oint_{\partial S} \vec{F}\cdot d\vec{s}=-128\pi

    [×]

    Solution

    By Stokes' Theorem, ∬S∇⃗×F⃗⋅dS⃗=∮∂SF⃗⋅ds⃗\displaystyle \iint_{S} \vec{\nabla}\times \vec{F}\cdot d\vec{S} =\oint_{\partial S} \vec{F}\cdot d\vec{s}. As a result, we can greatly simplify the integral by integrating over the boundary curve. Using cylindrical coordinates, the surface is: R⃗(r,θ)=⟨rcos⁡θ,rsin⁡θ,r4⟩ \vec R(r,\theta)=\left\langle r\cos\theta,r\sin\theta,r^4\right\rangle On the upper boundary where z=16z=16, we have (x2+y2)2=16x2+y2=4r=2\begin{aligned} (x^2+y^2)^2 &=16\\ x^2+y^2 &=4\\ r &=2 \end{aligned} So our circle boundary becomes r⃗(θ)=⟨2cos⁡θ,2sin⁡θ,16⟩ \vec r(\theta)=\left\langle 2\cos\theta,2\sin\theta,16 \right\rangle Using this, we find the velocity: v⃗(θ)=⟨−2sin⁡θ,2cos⁡θ,0⟩ \vec v(\theta)=\left\langle -2\sin\theta,2\cos\theta,0 \right\rangle We need the surface oriented down and out. So we must traverse the boundary circle clockwise. This v⃗\vec v is counterclockwise. So we reverse it: v⃗(θ)=⟨2sin⁡θ,−2cos⁡θ,0⟩ \vec v(\theta)=\left\langle 2\sin\theta,-2\cos\theta,0 \right\rangle The vector field F⃗=⟨−yz,xz,xyz⟩\vec{F}=\langle-yz,xz,xyz\rangle becomes: F⃗∣r⃗(θ)=⟨−32sin⁡θ,32cos⁡θ,64sin⁡θcos⁡θ⟩ \left.\vec{F}\right|_{\vec r(\theta)} =\langle -32\sin\theta,32\cos\theta,64\sin\theta\cos\theta \rangle Their dot product is: F⃗⋅v⃗=−64sin⁡2θ−64cos⁡2θ=−64\begin{aligned} \vec{F}\cdot\vec{v} &=-64\sin^2\theta-64\cos^2\theta\\ &=-64 \end{aligned} Finally find the value of the line integral is: ∮∂SF⃗⋅ds⃗=∫02π−64dθ=−128π\begin{aligned} \oint_{\partial S}\vec{F}\cdot d\vec{s} =\int_{0}^{2\pi}-64\,d\theta = -128\pi \end{aligned}

    [×]

  3. Compute ∬H∇⃗×F⃗⋅dS⃗\displaystyle \iint_H \vec{\nabla}\times\vec{F}\cdot d\vec{S} for F=⟨−3y,3x,x2+y2⟩F=\left\langle-3y,3x,\sqrt{x^2+y^2}\right\rangle over the hyperbolic paraboloid, HH, given by z=xyz=xy oriented upward inside the cylinder x2+y2=9x^2+y^2=9 by using Stokes' Theorem.
    You can rotate the second plot with your mouse.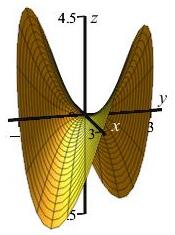

    x_hyp_parab_xy
    1

    Hint

    Starting from cylindrical coordinates: R⃗(r,θ,z)=(rcos⁡θ,rsin⁡θ,z) \vec R(r,\theta,z)=(r\cos\theta,r\sin\theta,z) the surface is z=xy=r2sin⁡θcos⁡θz=xy=r^2\sin\theta\cos\theta which may be parametrized as: R⃗(r,θ)=(rcos⁡θ,rsin⁡θ,r2sin⁡θcos⁡θ) \vec R(r,\theta)=(r\cos\theta,r\sin\theta,r^2\sin\theta\cos\theta) The boundary is at r=3r=3. So the boundary circle may be parametrized as: r⃗(θ)=(3cos⁡θ,3sin⁡θ,9sin⁡θcos⁡θ) \vec r(\theta)=(3\cos\theta,3\sin\theta,9\sin\theta\cos\theta)

    [×]

    Answer

    ∬H∇⃗×F⃗⋅dS⃗=∮∂HF⃗⋅ds⃗=54π\displaystyle \iint_H \vec{\nabla}\times\vec{F}\cdot d\vec{S} =\oint_{\partial H}\vec{F}\cdot d\vec{s}=54\pi

    [×]

    Solution

    We will use Stokes' Theorem ∬H∇⃗×F⃗⋅dS⃗=∮∂HF⃗⋅ds⃗\displaystyle \iint\limits_H \vec{\nabla}\times \vec{F}\cdot d\vec{S} =\oint\limits_{\partial H}\vec{F}\cdot d\vec{s} to simplify the integral.

    Starting from cylindrical coordinates: R⃗(r,θ,z)=(rcos⁡θ,rsin⁡θ,z) \vec R(r,\theta,z)=(r\cos\theta,r\sin\theta,z) the surface is z=xy=r2sin⁡θcos⁡θz=xy=r^2\sin\theta\cos\theta which may be parametrized as: R⃗(r,θ)=(rcos⁡θ,rsin⁡θ,r2sin⁡θcos⁡θ) \vec R(r,\theta)=(r\cos\theta,r\sin\theta,r^2\sin\theta\cos\theta) The boundary is at r=3r=3. So the boundary circle may be parametrized as: r⃗(θ)=(3cos⁡θ,3sin⁡θ,9sin⁡θcos⁡θ) \vec r(\theta)=(3\cos\theta,3\sin\theta,9\sin\theta\cos\theta) The velocity is: v⃗(θ)=(−3sin⁡θ,3cos⁡θ,9cos⁡2θ−9sin⁡2θ) \vec v(\theta)=(-3\sin\theta,3\cos\theta,9\cos^{2}\theta-9\sin^{2}\theta) On the curve the vector field F=⟨−3y,3x,x2+y2⟩F=\left\langle-3y,3x,\sqrt{x^2+y^2}\right\rangle becomes F⃗=(−9sin⁡θ,9cos⁡θ,3)\vec{F}=(-9\sin\theta,9\cos\theta,3). So the integrand is: F⃗⋅v⃗=27sin⁡2θ+27cos⁡2θ+27cos⁡2θ−27sin⁡2θ=54cos⁡2θ\begin{aligned} \vec{F}\cdot\vec{v} &=27\sin^{2}\theta+27\cos^{2}\theta+27\cos^{2}\theta-27\sin^{2}\theta \\ &=54\cos^{2}\theta \end{aligned} Now the integral can be computed using the identity cos⁡2θ=1+cos⁡2θ2\cos^2\theta=\dfrac{1+\cos2\theta}{2}: ∮∂HF⃗⋅ds⃗=∫02π54cos⁡2θdθ=∫02π27(1+cos⁡2θ)dθ=27[θ+sin⁡2θ2]02π=54π\begin{aligned} \oint_{\partial H} \vec{F}\cdot d\vec{s} &=\int_{0}^{2\pi} 54\cos^{2}\theta\,d\theta =\int_{0}^{2\pi} 27\left(1+\cos2\theta\right)\,d\theta \\ &=27\left[\theta+\dfrac{\sin2\theta}{2}\right]_0^{2\pi} =54\pi \end{aligned}

    [×]

    4. b. Verification

  4. Verify Stokes' Theorem, ∬C∇⃗×F⃗⋅dS⃗=∮∂CF⃗⋅ds⃗\displaystyle \iint_C \vec{\nabla}\times\vec{F}\cdot d\vec{S} =\oint_{\partial C} \vec{F}\cdot d\vec{s}, for the cone CC given by z=x2+y2z=\sqrt{x^2+y^2} for z≤3z \le 3 oriented down and out, and the vector field F⃗=⟨−yz,xz,z2⟩\vec{F}=\langle-yz,xz,z^2\rangle

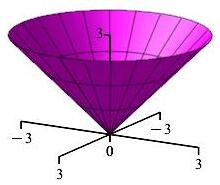
    x_full_cone

    1. LHS - Surface Integral:  Compute the left side.

      Hint

      Always compute the divergence in rectangular coordinates! When you are ready to do the integral, then you convert the divergence into the coordinates needed for the integral.

      [×]

      Answer

      ∬S∇⃗×F⃗⋅dS⃗=−54π\displaystyle \iint\limits_{S}\vec{\nabla}\times \vec{F}\cdot d\vec{S}=-54\pi

      [×]

      Solution

      To compute the left side, we first parametrize the cone, CC, as: R⃗(r,θ)=(rcos⁡θ,rsin⁡θ,r) \vec{R}\left( r,\theta \right) =\left( r\cos \theta ,r\sin \theta ,r\right) Next we find the normal vector: N⃗=e⃗r×e⃗θ=∣ı^ȷ^k^cos⁡θsin⁡θ1−rsin⁡θrcos⁡θ0∣=⟨−rcos⁡θ,−rsin⁡θ,r⟩\begin{aligned} \vec{N}&=\vec{e}_{r}\times \vec{e}_{\theta }= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \cos \theta & \sin \theta & 1 \\ -r\sin \theta & r\cos \theta & 0 \end{vmatrix}\\ &=\left\langle -r\cos \theta,-r\sin \theta,r\right\rangle \end{aligned} We reverse N⃗\vec{N} so it points down and out: N⃗=⟨rcos⁡θ,rsin⁡θ,−r⟩ \vec{N}=\left\langle r\cos\theta,r\sin\theta,-r\right\rangle We compute the curl of F⃗\vec F: ∇⃗×F⃗=∣ı^ȷ^k^∂x∂y∂z−yzxzz2∣=ı^(−x)−ȷ^(y)+k^(2z) \vec{\nabla}\times \vec{F} =\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \partial x & \partial y & \partial z \\ -yz & xz & z^{2} \end{vmatrix} =\hat{\imath}\left( -x\right) -\hat{\jmath}\left( y\right) +\hat{k}\left( 2z\right) On our parametrized surface, this is ∇⃗×F⃗=⟨−rcos⁡θ,−rsin⁡θ,2r⟩ \vec{\nabla}\times \vec{F} =\left\langle -r\cos \theta,-r\sin \theta,2r\right\rangle Its dot product with the normal is: ∇⃗×F⃗⋅N⃗=−r2cos⁡2θ−r2sin⁡2θ−2r2=−3r2 \vec{\nabla}\times \vec{F}\cdot\vec N =-r^2\cos^2\theta-r^2\sin^2\theta-2r^2 =-3r^2 Now we compute the integral: ∬∇⃗×F⃗⋅dS⃗=∫02π∫03∇⃗×F⃗⋅N⃗drdθ=∫02π∫03(−3r2)drdθ=2π[−r3]03=−54π\begin{aligned} \iint &\vec{\nabla}\times\vec{F}\cdot d\vec{S} =\int_{0}^{2\pi} \int_{0}^{3} \vec{\nabla}\times \vec{F}\cdot\vec N\,dr\,d\theta \\ &=\int_{0}^{2\pi} \int_{0}^{3} (-3r^{2})\,dr\,d\theta =2\pi\left[-r^{3}\right]_{0}^{3}=-54\pi \end{aligned}

      [×]

    2. RHS - Line Integral:  Compute the right side and verify the theorem.

      Answer

      ∮∂SF⃗⋅ds⃗=−54π\displaystyle\oint\limits_{\partial S}\vec{F}\cdot d\vec{s}=-54\pi

      [×]

      Solution

      To compute the right side, we parameterize the circle, x2+y2=9x^{2}+y^{2}=9, as: r⃗(θ)=(3cos⁡θ,3sin⁡θ,3) \vec{r}\left( \theta \right) =\left( 3\cos \theta,3\sin \theta ,3\right) So the velocity vector is v⃗(θ)=⟨−3sin⁡θ,3cos⁡θ,0⟩ \vec{v}(\theta)=\left\langle -3\sin \theta,3\cos \theta,0\right\rangle We reverse the velocity vector so it points counterclockwise: v⃗(θ)=⟨3sin⁡θ,−3cos⁡θ,0⟩ \vec{v}(\theta)=\left\langle 3\sin \theta ,-3\cos \theta,0\right\rangle Evaluating F⃗=⟨−yz,xz,z2⟩\vec{F}=\left\langle -yz,xz,z^{2}\right\rangle along the curve, we get: F⃗∣r⃗(θ)=⟨−9sin⁡θ,9cos⁡θ,9⟩ \left. \vec{F}\right\vert _{\vec{r}\left( \theta \right)} =\left\langle -9\sin \theta,9\cos \theta,9\right\rangle So the dot product F⃗⋅v⃗\vec{F}\cdot \vec v is: F⃗⋅v⃗=−27sin⁡2θ−27cos⁡2θ+0=−27 \vec{F}\cdot\vec v=-27\sin ^{2}\theta -27\cos ^{2}\theta +0=-27 Finally, we compute the line integral: ∮∂SF⃗⋅ds⃗=∫02π−27dθ=−54π \oint_{\partial S}\vec{F}\cdot d\vec{s}=\int_{0}^{2\pi}-27\,d\theta =-54\pi This matches the left side, so we have verified the theorem!

      [×]

  5. Verify Stokes Theorem for the part of the saddle surface (hyperbolic paraboloid), z=x2−y2z=x^2-y^2, oriented up, inside the cylinder x2+y2=4x^2+y^2 = 4 for the vector field, F⃗=⟨−y,x,2z⟩\vec F=\langle-y,x,2z\rangle.
    You can rotate the second plot with your mouse.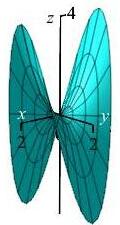

    x_hyp_parab_x^2-y^2
    1

    1. LHS - Surface Integral:  Compute the left side.

      Hint

      To parametrize the saddle surface, we start with cylindrical coordinates and set z=x2−y2=r2(cos⁡2θ−sin⁡2θ)=r2cos⁡2θz=x^2-y^2=r^2(\cos^2\theta-\sin^2\theta)=r^2\cos2\theta.

      [×]

      Answer

      ∬S∇⃗×F⃗⋅dS⃗=8π\displaystyle \iint_{S}\vec{\nabla}\times \vec{F}\cdot d\vec{S}=8\pi

      [×]

      Solution

      To compute the left side, we first parametrize the saddle surface using cylindrical coordinates. Setting x=rcos⁡θx=r\cos\theta and y=rsin⁡θy=r\sin\theta, we parametrize zz as: z=x2−y2=r2(cos⁡2θ−sin⁡2θ)=r2cos⁡2θ z=x^2-y^2=r^2(\cos^2\theta-\sin^2\theta)=r^2\cos2\theta From here, we take the cross product of the tangent vectors to obtain the normal vector: N⃗=e⃗r×e⃗θ=∣ı^ȷ^k^cos⁡θsin⁡θ2rcos⁡2θ−rsin⁡θrcos⁡θ−2r2sin⁡2θ∣=⟨−2r2(sin⁡θsin⁡2θ+cos⁡θcos⁡2θ),2r2(cos⁡θsin⁡2θ+sin⁡θcos⁡2θ),r⟩\begin{aligned} \vec{N}&=\vec{e}_{r}\times \vec{e}_{\theta }= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \cos \theta & \sin\theta & 2r\cos2\theta \\ -r\sin \theta & r\cos\theta & -2r^2\sin2\theta \end{vmatrix}\\ &=\langle -2r^2(\sin\theta\sin2\theta+\cos\theta\cos2\theta),\\ &\qquad2r^2(\cos\theta\sin2\theta+\sin\theta\cos2\theta),r\rangle \end{aligned} Because we want the surface oriented upwards and Nz=r>0N_z=r>0, we do not have to change the sign of the normal vector. Next, we compute the curl of the vector field F⃗=⟨−y,x,2z⟩\vec F=\langle-y,x,2z\rangle: ∇⃗×F⃗=∣ı^ȷ^k^∂x∂y∂z−yx2z∣=ı^(0)−ȷ^(0)+k^(2) \vec{\nabla}\times \vec{F} =\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \partial_x & \partial_y & \partial_z \\ -y & x & 2z \end{vmatrix} =\hat{\imath}(0)-\hat{\jmath}(0)+\hat{k}(2) Taking the dot product with the normal gives: ∇⃗×F⃗⋅N⃗=2r\vec\nabla\times\vec F\cdot\vec N=2r. Since we are inside the cylinder x2+y2=4x^2+y^2=4 the upper limit on rr is 22. Finally, we compute the surface integral: ∬S∇⃗×F⃗⋅dS⃗=∫02π∫02∇⃗×F⃗⋅N⃗drdθ=∫02π∫02(2r)drdθ=2π[r2]02=8π\begin{aligned} \iint_S&\vec{\nabla}\times\vec{F}\cdot d\vec{S} =\int_{0}^{2\pi} \int_{0}^{2} \vec{\nabla}\times \vec{F}\cdot\vec N\,dr\,d\theta \\ &=\int_{0}^{2\pi} \int_{0}^{2} (2r)\,dr\,d\theta =2\pi\left[r^{2}\right]_{0}^{2}=8\pi \end{aligned}

      [×]

    2. RHS - Line Integral:  Compute the right side and verify the theorem.

      Answer

      ∮∂SF⃗⋅ds⃗=8π\displaystyle \oint_{\partial S} \vec{F}\cdot d\vec{s}=8\pi

      [×]

      Solution

      First, we parametrize the boundary curve in cylindrical coordinates. Letting x=rcos⁡θx=r\cos\theta and y=rsin⁡θy=r\sin\theta, we can parametrize zz: z=x2−y2=r2(cos⁡2θ−sin⁡2θ)=r2cos⁡2θ z=x^2-y^2=r^2(\cos^2\theta-\sin^2\theta)=r^2\cos2\theta Our boundary curve where r=2r=2 is then: r⃗(θ)=⟨2cos⁡θ,2sin⁡θ,4cos⁡2θ⟩ \vec r(\theta)=\left\langle 2\cos\theta, 2\sin\theta, 4\cos2\theta\right\rangle So the velocity vector is: v⃗(θ)=⟨−2sin⁡θ,2cos⁡θ,−8sin⁡2θ⟩ \vec v(\theta)=\left\langle -2\sin\theta, 2\cos\theta, -8\sin2\theta\right\rangle Since the orientation is up, we want the velocity to point counterclockwise when looking from above. The velocity already points counterclockwise so we need not reverse it.

      We evaluate F⃗=⟨−y,x,2z⟩\vec F=\langle -y,x,2z\rangle on the surface: F⃗∣r⃗(θ)=⟨−2sin⁡θ,2cos⁡θ,8cos⁡2θ⟩ \left.\vec F\right |_{\vec r(\theta)} =\langle -2\sin\theta,2\cos\theta,8\cos2\theta \rangle The dot product with the velocity is: F⃗⋅v⃗=⟨−2sin⁡θ,2cos⁡θ,8cos⁡2θ⟩⋅⟨−2sin⁡θ,2cos⁡θ,−8sin⁡2θ⟩=4sin⁡2θ+4cos⁡2θ−64sin⁡2θcos⁡2θ=4−32sin⁡4θ\begin{aligned} \vec F \cdot\vec v &=\langle -2\sin\theta,2\cos\theta,8\cos2\theta \rangle \cdot \left\langle -2\sin\theta, 2\cos\theta,-8\sin2\theta\right\rangle\\ &=4\sin^{2}\theta+4\cos^{2}\theta-64\sin2\theta\cos2\theta =4-32\sin4\theta \end{aligned} where we used the identity sin⁡2A=2sin⁡Acos⁡A\sin2A=2\sin A\cos A. Finally, we compute the integral: ∮∂SF⃗⋅ds⃗=∫02π(4−32sin⁡4θ)dθ=[4θ+8cos⁡4θ]02π=8π\begin{aligned} \oint\limits_{\partial S}\vec{F}\cdot d\vec{s} &=\int_0^{2\pi} (4-32\sin4\theta)\,d\theta\\ &=\left[4\theta+8\cos4\theta\right]_0^{2\pi}=8\pi \end{aligned}

      [×]

  6. Verify Stokes' Theorem, ∬S∇⃗×F⃗⋅dS⃗=∮∂SF⃗⋅ds⃗\displaystyle \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} =\oint_{\partial S} \vec{F}\cdot d\vec{s}, for the cylinder SS given by x2+y2=9x^2+y^2=9 for 1≤z≤21 \le z \le 2, oriented outward, and the vector field F⃗=⟨yz2,−xz2,z3⟩\vec{F}=\langle yz^2,-xz^2,z^3\rangle.

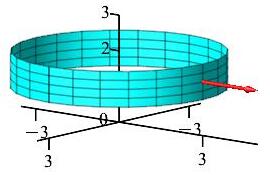
    x_cyl_r3_z1_2

    1. LHS - Surface Integral:  Compute the left side.

      Answer

      ∬S∇⃗×F⃗⋅dS⃗=54π\displaystyle \iint_{S} \vec{\nabla}\times\vec{F}\cdot d\vec{S} =54\pi

      [×]

      Solution

      To compute the left side, we parameterize the cylinder as: R⃗(θ,z)=⟨3cos⁡θ,3sin⁡θ,z⟩ \vec{R}\left( \theta ,z\right) =\left\langle 3\cos \theta,3\sin \theta,z\right\rangle First we find the tangent vectors and the normal vector: N⃗=e⃗θ×e⃗z=∣ı^ȷ^k^−3sin⁡θ3cos⁡θ0001∣=⟨3cos⁡θ,3sin⁡θ,0⟩\begin{aligned} \vec{N}&=\vec{e}_{\theta}\times \vec{e}_{z}= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ -3\sin \theta & 3\cos \theta & 0 \\ 0 & 0 & 1 \end{vmatrix}\\ &=\left\langle 3\cos \theta,3\sin \theta,0\right\rangle \end{aligned} This has the correct orientation. Next we compute the curl of F⃗\vec F and evaluate it on the surface: ∇⃗×F⃗∣R⃗(r,θ)=∣ı^ȷ^k^∂x∂y∂zyz2−xz2z3∣=ı^(0+2xz)−ȷ^(−2yz)+k^(−z2−z2)=⟨2xz,2yz,−2z2⟩=⟨6zcos⁡θ,6zsin⁡θ,−2z2⟩\begin{aligned} \vec{\nabla}\times \left.\vec{F}\right|_{\vec{R}(r,\theta)}&= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \partial_x & \partial_y & \partial_z \\ yz^{2} & -xz^{2} & z^{3} \end{vmatrix}\\ &=\hat{\imath}\left( 0+2xz\right) -\hat{\jmath}\left( -2yz\right) +\hat{k} \left( -z^{2}-z^{2}\right)\\ &=\left\langle 2xz,2yz,-2z^{2}\right\rangle\\ &=\left\langle 6z\cos \theta,6z\sin \theta,-2z^{2}\right\rangle \end{aligned} Now we find the dot product of the curl and the normal: ∇⃗×F⃗⋅N⃗=⟨6zcos⁡θ,6zsin⁡θ,−2z2⟩⋅⟨3cos⁡θ,3sin⁡θ,0⟩=18zcos⁡2θ+18zsin⁡2θ=18z\begin{aligned} \vec{\nabla}\times \vec{F}\cdot \vec N &=\left\langle 6z\cos\theta,6z\sin \theta,-2z^{2}\right\rangle \cdot \left\langle 3\cos \theta,3\sin \theta,0\right\rangle \\ &=18z\cos ^{2}\theta +18z\sin ^{2}\theta=18z \end{aligned} Finally, we compute the integral: ∬S∇⃗×F⃗⋅dS⃗=∫02π∫12(18z)dzdθ=2π[9z2]12=54π\begin{aligned} \iint_{S} \vec{\nabla}\times\vec{F} \cdot d\vec{S} &=\int_{0}^{2\pi }\int_{1}^{2}\left( 18z\right) \,dz\,d\theta\\ &=2\pi \left[ 9z^{2}\right] _{1}^{2}=54\pi \end{aligned}

      [×]

    2. RHS - Line Integral:  Compute the right side and verify the theorem.

      Hint

      The surface has two boundary curves. You must find the line integral over both and add them.

      [×]

      Answer

      ∮∂SF⃗⋅ds⃗=54π\displaystyle \oint_{\partial S} \vec{F}\cdot d\vec{s}=54\pi

      [×]

      Solution

      To compute the right side, we parameterize the two circles, find their velocity vector, and compute the dot products and integrals. The upper circle can be parameterized as: r⃗(θ)=⟨3cos⁡θ,3sin⁡θ,2⟩ \vec{r}\left( \theta \right) =\left\langle 3\cos \theta,3\sin \theta, 2\right\rangle So the velocity vector is: v⃗(θ)=⟨−3sin⁡θ,3cos⁡θ,0⟩ \vec{v}(\theta)=\left\langle -3\sin \theta,3\cos \theta,0\right\rangle By the right hand rule, the upper curve must be traversed clockwise. The v⃗\vec{v} above points counterclockwise, so we have to reverse it: v⃗(θ)=⟨3sin⁡θ,−3cos⁡θ,0⟩ \vec{v}(\theta)=\left\langle 3\sin\theta,-3\cos \theta,0\right\rangle From here, we evaluate F⃗=⟨yz2,−xz2,z3⟩\vec{F}=\left\langle yz^2,-xz^2,z^3\right\rangle along the curve: F⃗∣r⃗(θ)=⟨12sin⁡θ,−12cos⁡θ,8⟩ \left. \vec{F}\right\vert _{\vec{r}\left( \theta \right) } =\left\langle 12\sin\theta,-12\cos \theta,8\right\rangle Its dot product with the velocity is: F⃗⋅v⃗=36sin⁡2θ+36cos⁡2θ=36 \vec{F}\cdot \vec{v} =36\sin^{2}\theta+36\cos^{2}\theta=36 Finally, we obtain the integral: ∮upperF⃗⋅ds⃗=∫02π36dθ=72π \oint\limits_{\text{upper}}\vec{F}\cdot d\vec{s} =\int_{0}^{2\pi}36\,d\theta =72\pi The lower circle can be parameterized as r⃗(θ)=⟨3cos⁡θ,3sin⁡θ,1⟩ \vec{r}(\theta)=\left\langle 3\cos \theta,3\sin \theta, 1\right\rangle So the velocity vector is v⃗(θ)=⟨−3sin⁡θ,3cos⁡θ,0⟩ \vec{v}(\theta)=\left\langle -3\sin \theta,3\cos \theta,0\right\rangle By the right hand rule, the lower curve must be traversed counterclockwise. The v⃗\vec{v} above points counterclockwise, so we do not need to reverse it. Again, we evaluate F⃗=⟨yz2,−xz2,z3⟩\vec{F}=\left\langle yz^2,-xz^2,z^3\right\rangle along the curve: F⃗∣r⃗(θ)=⟨3sin⁡θ,−3cos⁡θ,1⟩ \left. \vec{F}\right\vert _{\vec{r}\left( \theta \right) } =\left\langle 3\sin\theta,-3\cos \theta,1\right\rangle and find its dot product with the velocity: F⃗⋅v⃗=−9sin⁡2θ−9cos⁡2θ=−9 \vec{F}\cdot \vec{v} =-9\sin ^{2}\theta -9\cos ^{2}\theta =-9 We obtain the integral: ∮lowerF⃗⋅ds⃗=∫02π−9dθ=−18π \oint\limits_{\text{lower}} \vec{F}\cdot d\vec{s} =\int_{0}^{2\pi}-9\,d\theta =-18\pi Finally, we sum the two line integrals to compute the total right hand side: ∮∂SF⃗⋅ds⃗=72π−18π=54π \oint_{\partial S}\vec{F}\cdot d\vec{s}=72\pi -18\pi=54\pi which agrees with the left side.

      [×]

  7. Verify Stoke's Theorem on the frustum of the cone z=rz=r with 1≤z≤41\le z \le 4, oriented up and in for the vector field G⃗=⟨−yz,xz,z(x2+y2)⟩\vec G=\langle -yz,xz,z(x^2+y^2)\rangle.
    You can rotate the second plot with your mouse.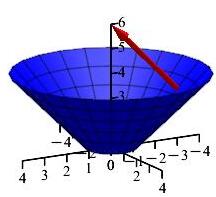

    Verify2-Exercise
    1

    1. LHS - Surface Integral:  Compute the left side.

      Answer

      ∬S∇⃗×G⃗⋅dS⃗=126π\displaystyle \iint_{S} \vec{\nabla}\times\vec{G} \cdot d\vec{S}=126\pi

      [×]

      Solution

      To compute the left side, we must find the normal, take the curl of the vector field and evaluate it on the surface. Then, we take their dot product and integrate.

      We parametrize the frustum as: R⃗(r,θ)=⟨rcos⁡θ,rsin⁡θ,r⟩ \vec R(r,\theta)=\left\langle r\cos\theta,r\sin\theta,r\right\rangle The normal vector is: N⃗=e⃗r×e⃗θ=∣ı^ȷ^k^cos⁡θsin⁡θ1−rsin⁡θrcos⁡θ0∣=⟨−rcos⁡θ,−rsin⁡θ,r⟩\begin{aligned} \vec{N}&=\vec{e}_{r}\times \vec{e}_{\theta}= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \cos\theta & \sin\theta & 1 \\ -r\sin \theta & r\cos \theta & 0 \end{vmatrix}\\ &=\left\langle -r\cos \theta,-r\sin \theta,r\right\rangle \end{aligned} This normal vector points up and in, as required. We compute the curl of the vector field G⃗=⟨−yz,xz,z(x2+y2)⟩\vec G=\langle -yz,xz,z(x^2+y^2)\rangle and then evaluate it on the surface: ∇⃗×G⃗=∣ı^ȷ^k^∂x∂y∂z−yzxzz(x2+y2)∣=ı^(2yz−x)−ȷ^(2xz+y)+k^(z+z)∇⃗×G⃗∣R⃗(r,θ)=⟨2r2sin⁡θ−rcos⁡θ,−2r2cos⁡θ−rsin⁡θ,2r⟩\begin{aligned} \vec{\nabla}\times\vec{G} &=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \partial_x & \partial_y & \partial_z \\ -yz & xz & z(x^2+y^2) \end{vmatrix}\\ &=\hat{\imath}\left(2yz-x\right)-\hat{\jmath}\left(2xz+y\right)+\hat{k} \left(z+z\right)\\ \vec{\nabla}\times \left.\vec{G}\right|_{\vec{R}(r,\theta)} &=\left\langle 2r^2\sin\theta-r\cos\theta,-2r^2\cos\theta-r\sin\theta, 2r\right\rangle \end{aligned} The dot product of the curl and the normal is: ∇⃗×G⃗⋅N⃗=−2r3sin⁡θcos⁡θ+r2cos⁡2θ+2r3sin⁡θcos⁡θ+r2sin⁡2θ+2r2=3r2 \begin{aligned} \vec\nabla\times\vec G \cdot\vec N &=-2r^3\sin\theta\cos\theta+r^2\cos^2\theta\\ &\quad\quad +2r^3\sin\theta\cos\theta+r^2\sin^2\theta+2r^2\\ &=3r^2 \end{aligned} Finally, we integrate over the surface: ∬S∇⃗×G⃗⋅dS⃗=∫02π∫143r2drdθ=2π[r3]14=126π \begin{aligned} \iint_{S} \vec{\nabla}\times\vec{G} \cdot d\vec{S} &=\int_0^{2\pi}\int_1^4 3r^2\,dr\,d\theta\\ &=2\pi\left[r^3\right]_1^4=126\pi \end{aligned}

      [×]

    2. RHS - Line Integral:  Compute the right side and verify the theorem.

      Hint

      The surface has two boundary curves. You must integrate over both. Since the normal points up and in, in which direction must they be traversed?

      [×]

      Answer

      ∮∂SF⃗⋅ds⃗=126π\displaystyle \oint_{\partial S}\vec{F}\cdot d\vec{s}=126\pi

      [×]

      Solution

      First, we calculate the line integral over the top curve. Since the normal points up and in, we must traverse this curve counterclockwise. We parametrize the upper circle as: r⃗(θ)=⟨4cos⁡θ,4sin⁡θ,4⟩ \vec r(\theta)=\langle 4\cos\theta,4\sin\theta,4\rangle The velocity is: v⃗(θ)=⟨−4sin⁡θ,4cos⁡θ,0⟩ \vec v(\theta)=\langle -4\sin\theta,4\cos\theta,0\rangle This velocity is counterclockwise, so we do not need to reverse it. We evaluate the vector field G⃗=⟨−yz,xz,z(x2+y2)⟩\vec G=\langle -yz,xz,z(x^2+y^2)\rangle on the boundary: G⃗∣r⃗(θ)=⟨−16sin⁡θ,16cos⁡θ,64⟩ \left.\vec G \right |_{\vec r(\theta)} =\langle -16\sin\theta,16\cos\theta,64\rangle Then, we take the dot product of G⃗\vec G and v⃗\vec v: G⃗⋅v⃗=⟨−16sin⁡θ,16cos⁡θ,64⟩⋅⟨−4sin⁡θ,4cos⁡θ,0⟩=64sin⁡2θ+64cos⁡2θ=64\begin{aligned} \vec G\cdot \vec v &=\langle -16\sin\theta,16\cos\theta,64\rangle \cdot \langle -4\sin\theta,4\cos\theta,0\rangle\\ &=64\sin^2\theta+64\cos^2\theta=64 \end{aligned} Finally, we compute the integral: ∮upperF⃗⋅ds⃗=∫02π64dθ=128π \oint\limits_{\text{upper}}\vec F\cdot d\vec s =\int_0^{2\pi}64\,d\theta=128\pi

      We must now do the same on the lower boundary. We parametrize the cirle: r⃗(θ)=⟨cos⁡θ,sin⁡θ,1⟩ \vec r(\theta)=\langle \cos\theta,\sin\theta,1\rangle The velocity is: v⃗(θ)=⟨−sin⁡θ,cos⁡θ,0⟩ \vec v(\theta)=\langle -\sin\theta,\cos\theta,0\rangle This velocity is counterclockwise, but we want it to be clockwise. So, we must reverse the signs: v⃗(θ)=⟨sin⁡θ,−cos⁡θ,0⟩ \vec v(\theta)=\langle \sin\theta,-\cos\theta,0\rangle We evaluate the vector field G⃗=⟨−yz,xz,z(x2+y2)⟩\vec G=\langle -yz,xz,z(x^2+y^2)\rangle on the boundary: G⃗∣r⃗(θ)=⟨−sin⁡θ,cos⁡θ,1⟩ \left.\vec G \right |_{\vec r(\theta)} =\langle -\sin\theta,\cos\theta,1 \rangle Then, we take the dot product of G⃗\vec G and v⃗\vec v: G⃗⋅v⃗=⟨−sin⁡θ,cos⁡θ,1⟩⋅⟨sin⁡θ,−cos⁡θ,0⟩=−sin⁡2θ−cos⁡2θ=−1\begin{aligned} \vec G\cdot \vec v &=\langle -\sin\theta,\cos\theta,1\rangle \cdot \langle \sin\theta,-\cos\theta,0\rangle\\ &=-\sin^2\theta-\cos^2\theta=-1 \end{aligned} Finally, we compute the integral: ∮lowerF⃗⋅ds⃗=∫02π−1dθ=−2π \oint\limits_{\text{lower}}\vec F\cdot d\vec s =\int_0^{2\pi}-1\,d\theta=-2\pi To complete the boundary integral, we add the integrals: ∮∂SF⃗⋅ds⃗=∮upperF⃗⋅ds⃗+∮lowerF⃗⋅ds⃗=128π−2π=126π\begin{aligned} \oint\limits_{\partial S}\vec F\cdot d\vec s &=\oint\limits_{\text{upper}}\vec F\cdot d\vec s +\oint\limits_{\text{lower}}\vec F\cdot d\vec s \\ &=128\pi-2\pi=126\pi \end{aligned} Since this is the same answer as part (a), we have verified Stokes' Theorem for this surface.

      [×]

    8. c. Proof

  8. Prove Stokes' Theorem for any parametric surface R⃗(u,v)\vec{R}(u,v) with parameter ranges a<u<ba \lt u \lt b and c<v<dc \lt v \lt d and a vector field F⃗=⟨0,Q(x,y,z),0⟩\vec{F}=\langle 0,Q(x,y,z),0\rangle.

    LHS: RHS:

    Hint

    You are trying to prove that ∬S∇⃗×F⃗⋅dS⃗=∮∂SF⃗⋅ds⃗ \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} =\oint_{\partial S} \vec{F}\cdot d\vec{s} Start by expanding out the dot product of the curl and the normal vector. What is the parametric chain rule? Is there any way to incorporate that here?

    [×]

    Solution

    Let S=R⃗(u,v)S=\vec R(u,v) be a nice parametric surface with parameter ranges a<u<ba \lt u \lt b and c<v<dc \lt v \lt d and let F⃗\vec F be a vector field in R3\mathbb{R}^3 such that F⃗=⟨0,Q(x,y,z),0⟩. \vec F=\langle 0,Q(x,y,z),0 \rangle . We must prove that ∬S∇⃗×F⃗⋅dS⃗=∮∂SF⃗⋅ds⃗. \iint_S \vec\nabla \times \vec F \cdot d\vec S =\oint_{\partial S} \vec F \cdot d\vec s. We start by computing the left hand side.

    LHS: We first evaluate the curl of F⃗\vec{F}: ∇⃗×F⃗=∣ı^ȷ^k^∂x∂y∂z0Q0∣=ı^(−∂zQ)−ȷ^(0)+k^(∂xQ)=⟨−∂zQ,0,∂xQ⟩=⟨−∂Q∂z,0,∂Q∂x⟩\begin{aligned} \vec{\nabla}\times\vec{F} &=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \partial_x & \partial_y & \partial_z \\ 0 & Q & 0 \end{vmatrix} =\hat{\imath}(-\partial_z Q)-\hat{\jmath}(0)+\hat{k}(\partial_x Q) \\ &=\langle -\partial_z Q,0,\partial_x Q\rangle =\left\langle -\dfrac{\partial Q}{\partial z},0, \dfrac{\partial Q}{\partial x}\right\rangle \end {aligned} For our own ease, we now represent the normal vector as Jacobians: N⃗=⟨∂(y,z)∂(u,v),∂(z,x)∂(u,v),∂(x,y)∂(u,v)⟩ \vec{N} =\left\langle\dfrac{\partial(y,z)}{\partial(u,v)}, \dfrac{\partial(z,x)}{\partial(u,v)}, \dfrac{\partial(x,y)}{\partial(u,v)}\right\rangle Then we compute the dot product, write out the Jacobians, and rearrange the terms: ∇⃗×F⃗⋅N⃗=⟨−∂Q∂z,0,∂Q∂x⟩⋅⟨∂(y,z)∂(u,v),∂(z,x)∂(u,v),∂(x,y)∂(u,v)⟩=−∂Q∂z∂(y,z)∂(u,v)+∂Q∂x∂(x,y)∂(u,v)=−∂Q∂z(∂y∂u∂z∂v−∂y∂v∂z∂u)+∂Q∂x(∂x∂u∂y∂v−∂x∂v∂y∂u)=∂y∂u(−∂Q∂z∂z∂v−∂Q∂x∂x∂v)+∂y∂v(∂Q∂z∂z∂u+∂Q∂x∂x∂u)\begin{aligned} \vec{\nabla}\times\vec{F}\cdot \vec{N} &=\left\langle -\dfrac{\partial Q}{\partial z},0, \dfrac{\partial Q}{\partial x}\right\rangle \cdot\left\langle\dfrac{\partial(y,z)}{\partial(u,v)}, \dfrac{\partial(z,x)}{\partial(u,v)}, \dfrac{\partial(x,y)}{\partial(u,v)}\right\rangle \\ &=-\dfrac{\partial Q}{\partial z}\dfrac{\partial(y,z)}{\partial(u,v)} +\dfrac{\partial Q}{\partial x}\dfrac{\partial(x,y)}{\partial(u,v)} \\ &=-\dfrac{\partial Q}{\partial z} \left(\dfrac{\partial y}{\partial u}\dfrac{\partial z}{\partial v} -\dfrac{\partial y}{\partial v}\dfrac{\partial z}{\partial u}\right) +\dfrac{\partial Q}{\partial x} \left(\dfrac{\partial x}{\partial u}\dfrac{\partial y}{\partial v} -\dfrac{\partial x}{\partial v}\dfrac{\partial y}{\partial u}\right) \\ &=\dfrac{\partial y}{\partial u} \left(-\dfrac{\partial Q}{\partial z}\dfrac{\partial z}{\partial v} -\dfrac{\partial Q}{\partial x}\dfrac{\partial x}{\partial v}\right) +\dfrac{\partial y}{\partial v} \left( \dfrac{\partial Q}{\partial z}\dfrac{\partial z}{\partial u} +\dfrac{\partial Q}{\partial x}\dfrac{\partial x}{\partial u}\right) \end{aligned} To simplify the above expression, we subtract the expression ∂Q∂y∂y∂u∂y∂v\dfrac{\partial Q}{\partial y}\dfrac{\partial y}{\partial u} \dfrac{\partial y}{\partial v} from the first term and add it to the second term. ∇⃗×F⃗⋅N⃗=∂y∂u(−∂Q∂z∂z∂v−∂Q∂x∂x∂v)+∂y∂v(∂Q∂z∂z∂u+∂Q∂x∂x∂u)−∂Q∂y∂y∂u∂y∂v+∂Q∂y∂y∂u∂y∂v=∂y∂u(−∂Q∂z∂z∂v−∂Q∂x∂x∂v−∂Q∂y∂y∂v)+∂y∂v(∂Q∂z∂z∂u+∂Q∂x∂x∂u+∂Q∂y∂y∂u)\begin{aligned} \vec{\nabla}\times\vec{F}\cdot \vec{N} &=\dfrac{\partial y}{\partial u} \left(-\dfrac{\partial Q}{\partial z}\dfrac{\partial z}{\partial v} -\dfrac{\partial Q}{\partial x}\dfrac{\partial x}{\partial v}\right) +\dfrac{\partial y}{\partial v} \left( \dfrac{\partial Q}{\partial z}\dfrac{\partial z}{\partial u} +\dfrac{\partial Q}{\partial x}\dfrac{\partial x}{\partial u}\right)\\ &\qquad\qquad -\dfrac{\partial Q}{\partial y}\dfrac{\partial y}{\partial u} \dfrac{\partial y}{\partial v} \qquad\qquad\qquad+\dfrac{\partial Q}{\partial y} \dfrac{\partial y}{\partial u}\dfrac{\partial y}{\partial v}\\ &=\dfrac{\partial y}{\partial u} \left(-\dfrac{\partial Q}{\partial z}\dfrac{\partial z}{\partial v} -\dfrac{\partial Q}{\partial x}\dfrac{\partial x}{\partial v} -\dfrac{\partial Q}{\partial y}\dfrac{\partial y}{\partial v}\right)\\ &\qquad\qquad\qquad +\dfrac{\partial y}{\partial v} \left( \dfrac{\partial Q}{\partial z}\dfrac{\partial z}{\partial u} +\dfrac{\partial Q}{\partial x}\dfrac{\partial x}{\partial u} +\dfrac{\partial Q}{\partial y}\dfrac{\partial y}{\partial u}\right) \end{aligned} Recognize that this can be condensed using the parametric chain rule: ∇⃗×F⃗⋅N⃗=−∂y∂u∂Q∘R⃗∂v+∂y∂v∂Q∘R⃗∂u \vec{\nabla}\times\vec{F}\cdot \vec{N} =-\dfrac{\partial y}{\partial u} \dfrac{\partial Q\circ\vec{R}}{\partial v} +\dfrac{\partial y}{\partial v} \dfrac{\partial Q\circ\vec{R}}{\partial u} We now add and subtract the term ∂2y∂u∂v(Q∘R⃗)\dfrac{\partial^2y}{\partial u\partial v}(Q\circ\vec{R}) so that each term becomes part of a product rule expansion: ∇⃗×F⃗⋅N⃗=−∂y∂u∂Q∘R⃗∂v−∂2y∂u∂v(Q∘R⃗)+∂y∂v∂Q∘R⃗∂u+∂2y∂u∂v(Q∘R⃗)=−∂∂v(∂y∂uQ∘R⃗)+∂∂u(∂y∂vQ∘R⃗)\begin{aligned} \vec{\nabla}\times\vec{F}\cdot \vec N &=-\dfrac{\partial y}{\partial u}\dfrac{\partial Q\circ\vec{R}}{\partial v} -\dfrac{\partial^2y}{\partial u\partial v}(Q\circ \vec{R}) +\dfrac{\partial y}{\partial v}\dfrac{\partial Q\circ\vec{R}}{\partial u} +\dfrac{\partial^2y}{\partial u\partial v}(Q\circ\vec{R})\\ &=-\dfrac{\partial }{\partial v} \left(\dfrac{\partial y}{\partial u}\,Q\circ\vec{R}\right) +\dfrac{\partial}{\partial u} \left(\dfrac{\partial y}{\partial v}\,Q\circ\vec{R}\right) \end{aligned} Now we incorporate this into the integral and split it into two pieces: ∬S∇⃗×F⃗⋅dS⃗=∫ab∫cd(−∂∂v(∂y∂uQ∘R⃗)+∂∂u(∂y∂vQ∘R⃗))dvdu=−∫ab∫cd∂∂v(∂y∂uQ∘R⃗)dvdu+∫ab∫cd∂∂u(∂y∂vQ∘R⃗)dvdu\begin{aligned} \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} &=\int_a^b\int_c^d \left(-\dfrac{\partial }{\partial v} \left(\dfrac{\partial y}{\partial u}\,Q\circ\vec{R}\right) +\dfrac{\partial}{\partial u} \left(\dfrac{\partial y}{\partial v}\,Q\circ\vec{R}\right)\right)\,dv\,du\\ &=-\int_a^b\int_c^d \dfrac{\partial }{\partial v} \left(\dfrac{\partial y}{\partial u}\,Q\circ\vec{R}\right)\,dv\,du +\int_a^b\int_c^d\dfrac{\partial}{\partial u} \left(\dfrac{\partial y}{\partial v}\,Q\circ\vec{R}\right)\,dv\,du \end{aligned} We interchange the order of integration in the second integral so that we can apply the Fundamental Theorem of Calculus to both terms: ∬S∇⃗×F⃗⋅dS⃗=−∫ab∫cd∂∂v(∂y∂uQ∘R⃗)dvdu+∫cd∫ab∂∂u(∂y∂vQ∘R⃗)dudv\begin{aligned} \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} &=-\int_a^b\int_c^d \dfrac{\partial }{\partial v} \left(\dfrac{\partial y}{\partial u}\,Q\circ\vec{R}\right)\,dv\,du +\int_c^d\int_a^b\dfrac{\partial}{\partial u} \left(\dfrac{\partial y}{\partial v}\,Q\circ\vec{R}\right)\,du\,dv\\ \end{aligned} =−∫ab[∂y∂uQ∘R⃗](u,v)=(u,c)(u,v)=(u,d)du+∫cd[∂y∂vQ∘R⃗](u,v)=(a,v)(u,v)=(b,v)dv\begin{aligned} &=-\int_a^b \left[\dfrac{\partial y}{\partial u}Q\circ\vec{R}\right]_{(u,v)=(u,c)}^{(u,v)=(u,d)}\,du +\int_c^d \left[\dfrac{\partial y}{\partial v}Q\circ\vec{R}\right]_{(u,v)=(a,v)}^{(u,v)=(b,v)}\,dv \end{aligned} Finally, we evaluate the functions and reorder the integrals: ∬S∇⃗×F⃗⋅dS⃗=∫abQ(R⃗(u,c))∂y∂u(u,c)du+∫cdQ(R⃗(b,v))∂y∂v(b,v)dv−∫abQ(R⃗(u,d))∂y∂u(u,d)du−∫cdQ(R⃗(a,v))∂y∂v(a,v)dv\begin{aligned} \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} &=\int_a^b Q\left(\vec{R}(u,c)\right)\dfrac{\partial y}{\partial u}(u,c)\,du +\int_c^d Q\left(\vec{R}(b,v)\right)\dfrac{\partial y}{\partial v}(b,v)\,dv \\ &-\int_a^b Q\left(\vec{R}(u,d)\right)\dfrac{\partial y}{\partial u}(u,d)\,du -\int_c^d Q\left(\vec{R}(a,v)\right)\dfrac{\partial y}{\partial v}(a,v)\,dv \end{aligned} We now want to see that this is the same as the integral on the right.

    [×]

    Solution

    RHS: To evaluate the right side of the equation, we must evaluate the integral over the closed curve which is the boundary of the surface, which in fact consists of four pieces: two uu-curves and two vv-curves. r⃗1(u)=R⃗(u,c)=(x(u,c),y(u,c),z(u,c))a<u<br⃗2(v)=R⃗(b,v)=(x(b,v),y(b,v),z(b,v))c<v<dr⃗3(u)=R⃗(u,d)=(x(u,d),y(u,d),z(u,d))a<u<br⃗4(v)=R⃗(a,v)=(x(a,v),y(a,v),z(a,v))c<v<d\begin{aligned} \vec{r}_1(u)&=\vec{R}(u,c)=\left(x(u,c),y(u,c),z(u,c)\right) \qquad a \lt u \lt b \\ \vec{r}_2(v)&=\vec{R}(b,v)=\left(x(b,v),y(b,v),z(b,v)\right) \qquad c \lt v \lt d \\ \vec{r}_3(u)&=\vec{R}(u,d)=\left(x(u,d),y(u,d),z(u,d)\right) \qquad a \lt u \lt b \\ \vec{r}_4(v)&=\vec{R}(a,v)=\left(x(a,v),y(a,v),z(a,v)\right) \qquad c \lt v \lt d \end{aligned} As in the proof of Green's Theorem, we must travel counterclockwise around the boundary curve but this time as seen from the tip of the normal N⃗\vec{N}. If we put our eye at the tip of N⃗=e⃗u×e⃗v\vec{N}=\vec{e}_u\times\vec{e}_v, we can rotate our head so that e⃗u\vec{e}_u points to the right and e⃗v\vec{e}_v points up. Then the uu-coordinate increases from left to right and the vv-coordinate increases from bottom to top. To implement the counterclockwise orientation, we must reverse the orientation of r⃗3\vec{r}_3 and r⃗4\vec{r}_4, which we will do by simply putting a minus sign in front of their integrals. So the integral on the right is: ∮∂SF⃗⋅ds⃗=∫r⃗1Qdy+∫r⃗2Qdy−∫r⃗3Qdy−∫r⃗4Qdy \oint_{\partial S} \vec{F}\cdot d\vec{s} =\int_{\vec{r}_1} Q\,dy+\int_{\vec{r}_2} Q\,dy -\int_{\vec{r}_3} Q\,dy-\int_{\vec{r}_4} Q\,dy To evaluate these integrals, we must evaluate the function, QQ, and the differential, dxdx, on each curve: ∮∂SF⃗⋅ds⃗=∫abQ(R⃗(u,c))∂y∂u(u,c)du+∫cdQ(R⃗(b,v))∂y∂v(b,v)dv−∫abQ(R⃗(u,d))∂y∂u(u,d)du−∫cdQ(R⃗(a,v))∂y∂v(a,v)dv\begin{aligned} \oint_{\partial S} \vec{F}\cdot d\vec{s} &=\int_a^b Q\left(\vec{R}(u,c)\right)\dfrac{\partial y}{\partial u}(u,c)\,du +\int_c^d Q\left(\vec{R}(b,v)\right)\dfrac{\partial y}{\partial v}(b,v)\,dv \\ &-\int_a^b Q\left(\vec{R}(u,d)\right)\dfrac{\partial y}{\partial u}(u,d)\,du -\int_c^d Q\left(\vec{R}(a,v)\right)\dfrac{\partial y}{\partial v}(a,v)\,dv \end{aligned}

    Conclusion: This is the same result we found on the left side. So the theorem is proved for the case that F⃗=⟨0,Q,0⟩\vec{F}=\langle 0,Q,0\rangle

    [×]

  9. Prove Stokes' Theorem for any parametric surface R⃗(u,v)\vec{R}(u,v) with parameter ranges a<u<ba \lt u \lt b and c<v<dc \lt v \lt d and a vector field F⃗=⟨0,0,T(x,y,z)⟩\vec{F}=\langle 0,0,T(x,y,z)\rangle.

    Hint

    We are trying to prove that ∬S∇⃗×F⃗⋅dS⃗=∮∂SF⃗⋅ds⃗ \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} =\oint_{\partial S} \vec{F}\cdot d\vec{s} Refer to the previous problem as well as the "proof" page in this text. We do not have a solution so that this problem can be assigned as homework.

    [×]

    10. d. Applications

  10. Consider a solid with the shape of an hourglass given in cylindrical coordinates by r=910∣z−3∣+15 r=\dfrac{9}{10}|z-3|+\dfrac{1}{5} between two disks AA and BB at z=1z=1 and z=5z=5, respectively. Note: We can check both disks have radius 22. Consider the vector field F⃗=⟨−yzx2+y2,xzx2+y2,0⟩\vec{F}=\left\langle -yz\sqrt{x^2+y^2},xz\sqrt{x^2+y^2},0\right\rangle.

    1. Compute ∬A∇⃗×F⃗⋅dS⃗\displaystyle \iint_A \vec{\nabla}\times\vec{F}\cdot d\vec{S} for the vector field F⃗\vec F with the disk, AA, oriented downward.

      Answer

      ∬A∇⃗×F⃗⋅dS⃗=−16π\displaystyle \iint_A \vec{\nabla}\times\vec{F}\cdot d\vec{S}=-16\pi

      [×]

      Solution

      First, we begin by parameterizing the top disk, AA, using a cylindrical coordinate system: R⃗A(r,θ)=⟨rcos⁡θ,rsin⁡θ,1⟩ \vec R_A(r,\theta)=\langle r\cos\theta,r\sin\theta,1 \rangle We use this to find the normal vector: N⃗=e⃗r×e⃗θ=∣ı^ȷ^k^cos⁡θsin⁡θ0−rsin⁡θrcos⁡θ0∣=⟨0,0,r⟩\begin{aligned} \vec{N}&=\vec{e}_{r}\times \vec{e}_{\theta}= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \cos\theta & \sin\theta & 0 \\ -r\sin\theta & r\cos\theta & 0 \end{vmatrix}\\ &=\left\langle 0, 0, r\right\rangle \end{aligned} This orientation is up but should be down for the bottom disk. So we reverse it: N⃗=⟨0,0,−r⟩ \vec{N}=\left\langle 0, 0, -r\right\rangle Then, we compute the curl of the vector field F⃗=⟨−yzx2+y2,xzx2+y2,0⟩\vec{F} =\left\langle -yz\sqrt{x^2+y^2},xz\sqrt{x^2+y^2},0\right\rangle: ∇⃗×F⃗=∣ı^ȷ^k^∂x∂y∂z−yzx2+y2xzx2+y20∣=ı^(0−xx2+y2)−ȷ^(0+yx2+y2)+k^(zx2x2+y2+zx2+y2+zy2x2+y2+zx2+y2)=⟨−xx2+y2,−yx2+y2,zx2+zy2x2+y2+2zx2+y2⟩=⟨−xx2+y2,−yx2+y2,zx2+y2+2zx2+y2⟩=⟨−xx2+y2,−yx2+y2,3zx2+y2⟩\begin{aligned} \vec{\nabla}\times\vec{F} &=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\[2pt] \partial_x & \partial_y & \partial_z \\[2pt] -yz\sqrt{x^2+y^2} & xz\sqrt{x^2+y^2} & 0 \end{vmatrix}\\[2pt] &=\hat{\imath}\left(0-x\sqrt{x^2+y^2}\right) -\hat{\jmath}\left(0+y\sqrt{x^2+y^2}\right)+\\ &\qquad\hat{k}\left(\dfrac{zx^2}{\sqrt{x^2+y^2}}+z\sqrt{x^2+y^2}+ \dfrac{zy^2}{\sqrt{x^2+y^2}}+z\sqrt{x^2+y^2} \right)\\ &=\left\langle -x\sqrt{x^2+y^2},-y\sqrt{x^2+y^2},\dfrac{zx^2+zy^2}{\sqrt{x^2+y^2}} +2z\sqrt{x^2+y^2} \right\rangle \\ &=\left\langle -x\sqrt{x^2+y^2},-y\sqrt{x^2+y^2}, z\sqrt{x^2+y^2}+2z\sqrt{x^2+y^2} \right\rangle\\ &=\left\langle -x\sqrt{x^2+y^2},-y\sqrt{x^2+y^2},3z\sqrt{x^2+y^2}\right\rangle \end{aligned} and evaluate it on the disk AA: ∇⃗×F⃗∣A=⟨−r2cos⁡θ,−r2sin⁡θ,3r⟩ \left.\vec{\nabla}\times\vec{F}\right|_{A} =\left\langle -r^2\cos\theta,-r^2\sin\theta,3r\right\rangle The dot product of the curl and the normal vector is: ∇⃗×F⃗⋅N⃗=−3r2 \vec\nabla\times\vec{F}\cdot\vec{N}=-3r^2 Finally, we evaluate the surface integral over AA: ∬A∇⃗×F⃗⋅dS⃗=∫02π∫02−3r2drdθ=−2π∫023r2dr=−16π\begin{aligned} \iint_A \vec{\nabla}\times\vec{F}\cdot d\vec{S} &=\int_0^{2\pi}\int_0^2 -3r^2\,dr\,d\theta \\ &=-2\pi\int_0^2 3r^2\,dr=-16\pi \end{aligned} Notice there is no extra factor of rr before the drdθdr\,d\theta because the Jacobian factor, rr, is already included in the N⃗\vec N.

      [×]

    2. Compute ∬B∇⃗×F⃗⋅dS⃗\displaystyle \iint_B \vec{\nabla}\times\vec{F}\cdot d\vec{S} for the vector field F⃗\vec F with the disk, BB, oriented upward.

      Answer

      ∬B∇⃗×F⃗⋅dS⃗=80π\displaystyle \iint_B \vec{\nabla}\times\vec{F}\cdot d\vec{S}=80\pi

      [×]

      Solution

      We compute the surface integral over BB in a very similar manner. First, using z=5z=5, we can parameterize BB: B⃗(r,θ)=⟨rcos⁡θ,rsin⁡θ,5⟩ \vec B(r,\theta)=\langle r\cos\theta,r\sin\theta,5\rangle Note that the normal vector is computed identically, with the only difference being that the orientation is now upward and so the normal does not need to be reversed: N⃗=⟨0,0,r⟩ \vec N=\langle 0,0,r \rangle The curl is computed identically but its value on the surface BB differs because now z=5z=5: ∇⃗×F⃗=⟨−xx2+y2,−yx2+y2,3zx2+y2⟩ \vec{\nabla}\times\vec{F} =\left\langle -x\sqrt{x^2+y^2},-y\sqrt{x^2+y^2},3z\sqrt{x^2+y^2}\right\rangle ∇⃗×F⃗∣B=⟨−r2cos⁡θ,−r2sin⁡θ,15r⟩ \vec{\nabla}\times \left.\vec{F}\right|_{B} =\left\langle -r^2\cos\theta,-r^2\sin\theta,15r\right\rangle Its dot product with the normal is now: ∇×F⃗⋅N⃗=15r2 \nabla\times\vec{F}\cdot\vec{N}=15r^2 Finally, we evaluate the surface integral over BB: ∬B∇⃗×F⃗⋅dS⃗=∫02π∫0215r2drdθ=2π∫0215r2dr=[10πr3]02=80π\begin{aligned} \iint_B &\vec{\nabla}\times\vec{F}\cdot d\vec{S} =\int_0^{2\pi}\int_0^2 15r^2\,dr\,d\theta \\ &=2\pi\int_0^2 15r^2\,dr=\left[10\pi r^3\right]_0^2=80\pi \end{aligned}

      [×]

    3. Compute ∬H∇⃗×F⃗⋅dS⃗\displaystyle \iint_H \vec{\nabla}\times\vec{F}\cdot d\vec{S} for the vector field F⃗\vec F over the sides of the hourglass, HH, oriented outward.

      Hint

      What does Stokes' Theorem tell us about a line integral over the boundary of this surface? How is this related to the answers in parts (a) and (b)?

      [×]

      Hint

      You already have all the information you need to solve this problem by using the answers from parts (a) and (b).

      [×]

      Answer

      ∬S∇⃗×F⃗⋅dS⃗=−64π\displaystyle \iint_S \vec\nabla\times\vec{F}\cdot d\vec{S}=-64\pi

      [×]

      Solution

      Observe that the boundary of the sides of the hourglass consists of two circles:
      C1C_1:   with radius r=2r=2 at z=1z=1 traversed counterclockwise, and
      C2C_2:   with radius r=2r=2 at z=5z=5 traversed clockwise.

      Notice that C1C_1 is also the boundary of disk AA and C2C_2 is also the boundary of disk BB. So we can replace the integrals over C1C_1 and C2C_2 by integrals over AA and BB. However, AA is oriented downward and so its boundary should be clockwise, whereas C1C_1 is counterclockwise. So we need a minus before the integral over AA. Likewise, BB is oriented upward and so its boundary should be counterclockwise, whereas C2C_2 is clockwise. So we also need a minus before the integral over BB.

      So by Stokes' Theorem, three times: ∬H∇⃗×F⃗⋅dS⃗=∮C1F⃗⋅ds⃗+∮C2F⃗⋅ds⃗=−∬A∇⃗×F⃗⋅dS⃗−∬B∇⃗×F⃗⋅dS⃗=16π−80π=−64π\begin{aligned} \iint_H \vec\nabla\times\vec{F}\cdot d\vec{S} &=\oint_{C_1}\vec{F}\cdot d\vec{s} +\oint_{C_2}\vec{F}\cdot d\vec{s} \\ &=-\iint_A \vec{\nabla}\times\vec{F}\cdot d\vec{S} -\iint_B \vec{\nabla}\times\vec{F}\cdot d\vec{S}\\ &=16\pi-80\pi=-64\pi \end{aligned}

      [×]

      Remark

      Alternatively, we could have computed the two line integrals, ∮C1F⃗⋅ds⃗\displaystyle \oint_{C_1}\vec{F}\cdot d\vec{s} and ∮C2F⃗⋅ds⃗\displaystyle \oint_{C_2}\vec{F}\cdot d\vec{s}, and used them to find the answers to (a), (b) and (c).

      [×]

  11. Consider the vector field F⃗=⟨yz,xz,xy⟩\displaystyle \vec{F}=\langle yz, xz, xy\rangle. This exercise will show F⃗\vec F is path independent. In other words, the integral ∫ABF⃗⋅ds⃗\displaystyle \int_A^B \vec{F}\cdot d\vec{s} is the same for any two curves CC which start at AA and end at BB. In particular, the integral is the same for all three of the curves:

    • C1C_1 is the helix r⃗1(θ)=(3cos⁡θ,2+3sin⁡θ,θ)\vec{r}_1(\theta)=(3\cos\theta, 2+3\sin\theta,\theta), for 0≤θ≤2π0\le\theta\le2\pi, shown in dashed red.

    • C2C_2 is the sine curve r⃗2(θ)=(3,2+3sin⁡θ,θ)\vec{r}_2(\theta)=(3, 2+3\sin\theta,\theta), for 0≤θ≤2π0\le\theta\le2\pi, shown in solid blue.

    • C3C_3 is the line segment r⃗3(θ)=(3,2,θ)\vec{r}_3(\theta)=(3, 2, \theta), for 0≤θ≤2π0\le \theta\le2\pi, shown in dotted magenta.

    1. Compute ∇⃗×F⃗\vec\nabla\times\vec F for F⃗=⟨yz,xz,xy⟩\displaystyle \vec{F}=\langle yz, xz, xy\rangle. Which theorem then guarantees F⃗\vec F is path independent?

      Answer

      ∇⃗×F⃗=0⃗\vec{\nabla}\times\vec{F}=\vec 0
      This integral is path independent by Stokes' Theorem.

      [×]

      Solution

      The curl is: ∇⃗×F⃗=∣ı^ȷ^k^∂x∂y∂zyzxzxy∣=ı^(x−x)−ȷ^(y−y)+k^(z−z)=⟨0,0,0⟩\begin{aligned} \vec{\nabla}\times\vec{F} &=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ \partial_x & \partial_y & \partial_z \\ yz & xz & xy \end{vmatrix} \\ &=\hat{\imath}(x-x)-\hat{\jmath}(y-y)+\hat{k}(z-z) \\ &=\langle 0,0,0\rangle \end{aligned} If we have 22 curves which start at AA and end at BB, like C1C_1 and C2C_2, then going along C1C_1 and backwards along C2C_2 is the boundary of a surface between them. So by Stokes' Theorem The integral along C1C_1 and backwards along C2C_2 is the integral over the surface between them of the curl of F⃗\vec F which is 0⃗\vec0. So the two line integrals are equal. It's path independent.

      [×]

    2. Verify the three curves, (i), (ii) and (iii), start and end at the same points AA and BB. Then pick one of the three of the curves and compute ∫ABF⃗⋅ds⃗\displaystyle \int_A^B \vec{F}\cdot d\vec{s}.

      Hint

      Which of the three curves looks easiest?

      [×]

      Answer

      r⃗1(0)=r⃗2(0)=r⃗3(0)=(3,2,0)\vec{r}_1(0)=\vec{r}_2(0)=\vec{r}_3(0)= (3,2,0)
      r⃗1(2π)=r⃗2(2π)=r⃗3(2π)=(3,2,2π)\vec{r}_1(2\pi)=\vec{r}_2(2\pi)=\vec{r}_3(2\pi)= (3,2,2\pi)
      ∫ABF⃗⋅ds⃗=12π\displaystyle \int_A^B \vec{F}\cdot d\vec{s}=12\pi

      [×]

      Solution

      All 33 curves start at: r⃗1(0)=(3cos⁡0,2+3sin⁡0,0)=(3,2,0)r⃗2(0)=(3,2+3sin⁡0,0)=(3,2,0)r⃗3(0)=(3,2,0)=(3,2,0)\begin{aligned} \vec{r}_1(0)&=(3\cos0,2+3\sin0,0) \!\!\!\!\!\! &&= (3,2,0)\\ \vec{r}_2(0)&=(3,2+3\sin0,0) \!\!\!\!\!\! &&= (3,2,0)\\ \vec{r}_3(0)&=(3,2,0) \!\!\!\!\!\! &&= (3,2,0)\\ \end{aligned} All 33 curves end at: r⃗1(2π)=(3cos⁡2π,2+3sin⁡2π,2π)=(3,2,2π)r⃗2(2π)=(3,2+3sin⁡2π,2π)=(3,2,2π)r⃗3(2π)=(3,2,2π)=(3,2,2π)\begin{aligned} \vec{r}_1(2\pi)&=(3\cos2\pi,2+3\sin2\pi,2\pi) \!\!\!\!\!\! &&= (3,2,2\pi)\\ \vec{r}_2(2\pi)&=(3,2+3\sin2\pi,2\pi) \!\!\!\!\!\! &&= (3,2,2\pi)\\ \vec{r}_3(2\pi)&=(3,2,2\pi) \!\!\!\!\!\! &&= (3,2,2\pi) \end{aligned} So A=(3,2,0)A=(3,2,0) and B=(3,2,2π)B=(3,2,2\pi). So the integral along the straight line where x=3x=3 and y=2y=2 is: ∫ABF⃗⋅ds⃗=∫02π⟨yz,xz,xy⟩⋅⟨0,0,1⟩dθ=∫02πxydθ=∫02π(3)(2)dθ=12π \begin{aligned} \int_A^B \vec{F}\cdot d\vec{s} &= \int_0^{2\pi} \langle yz, xz, xy\rangle \cdot \langle 0, 0, 1\rangle \, d\theta \\ &= \int_0^{2\pi} xy \, d\theta = \int_0^{2\pi} (3)(2) \, d\theta \\ &= 12\pi \end{aligned}

      tj 

      [×]

    3. Find a scalar potential for F⃗=⟨yz,xz,xy⟩\displaystyle \vec{F}=\langle yz, xz, xy\rangle. Which theorem then guarantees F⃗\vec F is path independent?

      Hint

      A scalar potential ff must satisfy ∇⃗f=F⃗\vec\nabla f=\vec F. Write out the three equations.

      [×]

      Answer

      f=xyzf=xyz
      This integral is path independent by the Fundamantal Theorem of Calculus for Curves.

      [×]

      Solution

      A scalar potential ff must satisfy ∇⃗f=F⃗\vec\nabla f=\vec F or: ∂xf=F1=yz∂yf=F1=xz∂xf=F1=xy \partial_xf=F_1=yz \qquad \partial_yf=F_1=xz \qquad \partial_xf=F_1=xy Integrating each says: f=xyz+g(y,z)f=xyz+h(x,z)f=xyz+k(xy) f = xyz + g(y,z) \qquad f = xyz + h(x,z) \qquad f = xyz + k(xy) The common solution is: f=xyzf = xyz The Fundamantal Theorem of Calculus for Curves then says this integral is path independent.

      tj 

      [×]

    4. Use the scalar potential for F⃗=⟨yz,xz,xy⟩\displaystyle \vec{F}=\langle yz, xz, xy\rangle to compute ∫ABF⃗⋅ds⃗\displaystyle \int_A^B \vec{F}\cdot d\vec{s} for all three of the curves r⃗1\vec r_1, r⃗2\vec r_2 and r⃗3\vec r_3.

      Hint

      The FTCC says ∫AB∇⃗f(r⃗i)⋅ds⃗=f(B)−F(A)\displaystyle \int_A^B\vec\nabla f(\vec{r}_i)\cdot d\vec s =f(B)-F(A)

      [×]

      Answer

      ∫ABF⃗(r⃗i)⋅ds⃗=12π\displaystyle \int_A^B\vec F(\vec{r}_i)\cdot d\vec s=12\pi

      [×]

      Solution

      Since A=(3,2,0)A=(3,2,0) and B=(3,2,2π)B=(3,2,2\pi), using the scalar potential, f=xyzf=xyz, and the FTCC, all three curves need the same computation: ∫ABF⃗(r⃗i)⋅ds⃗=∫AB∇⃗f(r⃗i)⋅ds⃗=f(B)−F(A)=(3)(2)(2π)−(3)(2)(0)=12π\begin{aligned} \int_A^B\vec F(\vec{r}_i)\cdot d\vec s &=\int_A^B\vec\nabla f(\vec{r}_i)\cdot d\vec s =f(B)-F(A) \\ &=(3)(2)(2\pi)-(3)(2)(0)=12\pi \end{aligned}

      tj 

      [×]

  12. The gas in a tank moves with a velocity vector of V⃗=⟨0,−2z,2x⟩\vec{V}=\langle 0,-2z,2x\rangle.
    You can rotate the second plot with your mouse.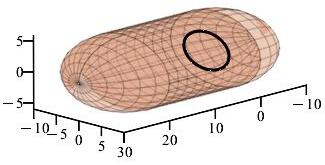

    x_circ_gas_tank
    1

    1. Find the circulation of the gas around the closed path r⃗(θ)=(2,5cos⁡θ,3sin⁡θ)\vec{r}(\theta)=(2,5\cos\theta,3\sin\theta) from θ=0\theta=0 to 2π2\pi.

      Hint

      The circulation of a vector F⃗\vec F is ∮∂SF⃗⋅ds⃗\displaystyle \oint_{\partial S} \vec F\cdot d\vec s . What is our vector field, and what is our closed curve?

      [×]

      Answer

      Circulation=∮∂SV⃗⋅ds⃗=30π\displaystyle \textrm{Circulation}=\oint_{\partial S} \vec V\cdot d\vec s=30\pi

      [×]

      Solution

      We find the tangent vector of our path: r⃗(θ)=(2,5cos⁡θ,3sin⁡θ)v⃗(θ)=(0,−5sin⁡θ,3cos⁡θ)\begin{aligned} \vec{r}(\theta)&=(2,5\cos\theta,3\sin\theta)\\ \vec{v}(\theta)&=(0,-5\sin\theta,3\cos\theta) \end{aligned} We restrict our fluid velocity V⃗\vec V to the curve r⃗(θ)\vec r(\theta): V⃗∣r⃗(θ)=⟨0,−6sin⁡θ,4⟩ \left.\vec V \right |_{\vec r(\theta)} =\left\langle 0,-6\sin\theta,4 \right\rangle We compute their dot product: V⃗⋅v⃗=30sin⁡2(θ)+12cos⁡(θ) \vec V\cdot\vec v=30\sin^2(\theta)+12\cos(\theta) Finally, we take the line integral using the above as our integrand: Circulation=∮∂SV⃗⋅ds⃗=∫02π30sin⁡2(θ)+12cos⁡(θ)dθ=∫02π30sin⁡2(θ)dθ+∫02π12cos⁡(θ)dθ=∫02π30(1−cos⁡2θ2)dθ+[12sin⁡(θ)]02π=15∫02π1−cos⁡2θdθ+0=15[θ−sin⁡(2θ)2]02π=30π\begin{aligned} \textrm{Circulation}&=\oint_{\partial S} \vec V\cdot d\vec s =\int_0^{2\pi} 30\sin^2(\theta)+12\cos(\theta)\,d\theta\\ &=\int_0^{2\pi} 30\sin^2(\theta)\,d\theta+ \int_0^{2\pi} 12\cos(\theta)\,d\theta\\ &=\int_0^{2\pi} 30\left(\dfrac{1-\cos2\theta}{2}\right)\,d\theta +\left[\rule{0pt}{10pt}12\sin(\theta)\right]_0^{2\pi} \\ &=15\int_0^{2\pi}1-\cos2\theta\,d\theta +0 \\ &=15\left[\theta-\dfrac{\sin(2\theta)}{2}\right]_0^{2\pi} =30\pi \end{aligned}

      tj 

      [×]

    2. What is the vorticity of the gas?

      Hint

      The vorticity is W⃗=∇⃗×V⃗\vec W=\vec\nabla\times\vec V.

      [×]

      Answer

      W⃗=⟨2,−2,0⟩\vec W=\langle 2,-2,0\rangle

      [×]

      Solution

      We simply compute the curl of V⃗=⟨0,−2z,2x⟩\vec V=\langle 0,-2z,2x\rangle. W⃗=∇⃗×V⃗=∣ı^ȷ^k^∂x∂y∂z0−2z2x∣=ı^(2)−ȷ^(2)+k^(0)=⟨2,−2,0⟩\begin{aligned} \vec W&=\vec{\nabla}\times\vec{V} =\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\[2pt] \partial_x & \partial_y & \partial_z \\[2pt] 0 & -2z & 2x \end{vmatrix}\\ &=\hat{\imath}(2)-\hat{\jmath}(2)+\hat{k}(0) =\langle 2,-2,0\rangle \end{aligned}

      tj 

      [×]

    3. Recompute the circulation for the curve in part (a), this time using the vorticity calculated in part (b). Notice that the curve is the boundary of the elliptical region: R⃗(t,θ)=⟨2,5tcos⁡θ,3tsin⁡θ⟩ \vec R(t,\theta)=\left\langle 2,5t\cos\theta,3t\sin\theta \right\rangle for 0≤t≤10\le t\le 1 and 0≤θ≤2π0\le \theta \le 2\pi.

      Answer

      Circulation=∬SW⃗⋅dS⃗=30π\displaystyle \textrm{Circulation}=\iint_{S}\vec{W}\cdot d\vec{S}=30\pi

      [×]

      Solution

      We begin by taking the normal vector of the surface: N⃗=e⃗t×e⃗θ=∣ı^ȷ^k^05cos⁡θ3sin⁡θ0−5tsin⁡θ3tcos⁡θ∣=⟨15t,0,0⟩\begin{aligned} \vec{N}&=\vec{e}_{t}\times \vec{e}_{\theta}= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ 0 & 5\cos\theta & 3\sin\theta \\ 0 & -5t\sin\theta & 3t\cos\theta \end{vmatrix}\\ &=\left\langle 15t, 0, 0\right\rangle \end{aligned} The dot product of vorticity from part (b), W⃗=⟨2,−2,0⟩\vec W=\langle 2,-2,0\rangle, and the normal is: W⃗⋅N⃗=⟨2,−2,0⟩⋅⟨15t,0,0⟩=30t \vec{W}\cdot\vec{N} =\langle 2,-2,0\rangle\cdot\langle 15t, 0, 0\rangle=30t Finally, we compute the surface integral: Circulation=∬SW⃗⋅N⃗dtdθ=∫02π∫0130tdtdθ=60π∫01tdt=60πt22∣01=30π\begin{aligned} \textrm{Circulation} &=\iint_{S}\vec{W}\cdot\vec{N}\,dt\,d\theta =\int_0^{2\pi}\int_0^1 30t\,dt\,d\theta\\ &=60\pi\int_0^1 t\,dt=\left.60\pi\dfrac{t^2}{2}\right|_{0}^{1}=30\pi \end{aligned}

      tj 

      [×]

      Remark

      Notice the circulation is the same whether computed as the line integral of the velocity or thesurface integral of the vorticity.

      [×]

  13. Water with velocity vector V⃗=⟨x,0,x22⟩\vec{V} =\left\langle x,0,\dfrac{x^2}{2}\right\rangle is flowing down a river.

    1. What is the vorticity of the water?

      Answer

      W⃗=⟨0,−x,0⟩ \vec W=\left\langle 0,-x,0\right\rangle

      [×]

      Solution

      We can compute the vorticity of the water using the formula: W⃗=∇⃗×V⃗ \vec W=\vec\nabla\times\vec{V} Since V⃗=⟨x,0,x22⟩\vec V=\left\langle x,0,\dfrac{x^2}{2}\right\rangle, we can easily take the curl: ∇⃗×V⃗=∣ı^ȷ^k^∂x∂y∂zx0x22∣=ı^(0)−ȷ^(x)+k^(0)=⟨0,−x,0⟩\begin{aligned} \vec{\nabla}\times\vec{V} &=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\[2pt] \partial_x & \partial_y & \partial_z \\[2pt] x & 0 & \dfrac{x^2}{2} \end{vmatrix}\\ &=\hat{\imath}(0)-\hat{\jmath}\left(x\right)+\hat{k}(0)\\ &=\left\langle 0,-x,0\right\rangle \end{aligned}

      [×]

    2. Use the vorticity to find the circulation of the water around the boundary of the rectangle in the plane of y=2y=2 where xx ranges from 00 to 33 and zz ranges from 00 to 22, orientated counterclockwise as seen from the positive yy-axis.
      You can rotate the second plot with your mouse.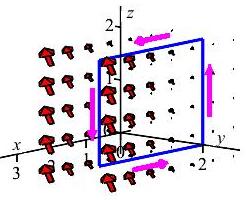

      x_circ_gas_rect
      1

      Answer

      Circulation=∬SW⃗⋅dS⃗=−25\displaystyle \textrm{Circulation}=\iint_{S}\vec{W}\cdot d\vec{S}=-25

      [×]

      Solution

      Recall the formula for circulation: Circulation=∮CV⃗⋅ds⃗ \textrm{Circulation}=\oint_{C}\vec{V}\cdot d\vec{s} Using Stokes' Theorem, we can put this in terms of the curl which we have already calculated: Circulation=∬S∇⃗×V⃗⋅dS⃗=∬SW⃗⋅dS⃗\begin{aligned} \textrm{Circulation} &=\iint_{S}\vec\nabla\times\vec{V}\cdot d\vec{S} \\ &=\iint_{S}\vec{W}\cdot d\vec{S} \end{aligned}

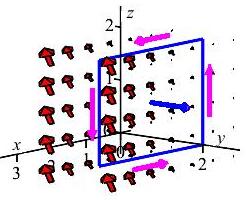
      x_circ_gas_rect_sol
      1

      Since dS⃗=N⃗dAd\vec{S}=\vec{N}\,dA, we need to compute the normal vector. We begin by parameterizing our rectangle: R⃗(s,t)=⟨t,2,s⟩ \vec R(s,t)=\langle t,2,s\rangle Where 0≤s≤20\le s\le 2 and 0≤t≤30\le t\le 3. Thus, the normal vector is: N⃗=e⃗s×e⃗t=∣ı^ȷ^k^001100∣=⟨0,1,0⟩\begin{aligned} \vec{N}&=\vec{e}_{s}\times \vec{e}_{t}= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{vmatrix}\\ &=\left\langle 0, 1, 0\right\rangle \end{aligned} This normal vector is pointing towards positive yy, which indicates a counterclockwise rotation. As a result, we do not need to reverse it. The vorticity evaluated on the surface is: W⃗=⟨0,−x,0⟩=⟨0,−t,0⟩ \vec W=\left\langle 0,-x,0\right\rangle =\left\langle 0,-t,0\right\rangle So the dot product of the vorticity and the normal vector is W⃗⋅N⃗=−t\vec W\cdot\vec N=-t. Using this, we compute the integral: Circulation=∬SW⃗⋅dS⃗=∫02∫03−tdtds=−2∫03td=−2[t22]03=−25\begin{aligned} \textrm{Circulation}&=\iint_{S}\vec{W}\cdot d\vec{S} =\int_0^2\int_0^3 -t\,dt\,ds\\ &=-2\int_0^3 t\,d =-2\left[\dfrac{t^2}{2}\right]_{0}^{3} =-25 \end{aligned} The minus indicates that the fluid is actually rotating clockwise.

      tj 

      [×]

    Note: In this problem it is easier to compute the circulation from the vorticity for two reasons. First, the curl is simple in this particular problem. Second, the direct line integral requires 44 separate integrals.

  14. The magnetic field B⃗=⟨x3,y2z,y3+yz2⟩\vec{B}=\langle x^3,y^2z,y^3+yz^2\rangle is produced by an the electrical current II flowing in the positive xx direction through the surface of a disk of radius 22 parallel to the yzyz-plane with center at (2,0,0)(2,0,0). Find II using:

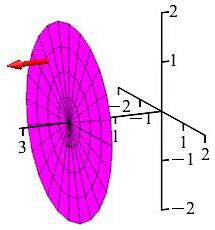
    x_ampere_disk

    1. the differential version of Ampere's Law.

      Answer

      I=3I=3

      [×]

      Solution

      Ampere's Law states that ∇⃗×B⃗=4πJ⃗ \vec\nabla\times\vec B=4\pi\vec{J} where B⃗\vec B is the magnetic field vector and J⃗\vec J is the electric current density vector. By Stokes' Theorem, we also have that I=∬SJ⃗⋅dS⃗ I=\iint_S \vec J\cdot d\vec{S} Since we know that J⃗\vec J is just ∇⃗×B⃗4π\dfrac{\vec \nabla\times\vec B}{4\pi}, we can compute the current by evaluating the following integral: I=14π∬S∇⃗×B⃗⋅dS⃗ I=\dfrac{1}{4\pi}\iint_S \vec\nabla \times\vec B \cdot d\vec{S} First, we parametrize the surface in terms of rr and θ\theta: R⃗(r,θ)=⟨2,rcos⁡θ,rsin⁡θ⟩ \vec R(r,\theta)=\langle 2,r\cos\theta,r\sin\theta \rangle Next, we take the normal vector of the surface: N⃗=e⃗r×e⃗θ=∣ı^ȷ^k^0cos⁡θsin⁡θ0−rsin⁡θrcos⁡θ∣=⟨r,0,0⟩\begin{aligned} \vec{N}&=\vec{e}_{r}\times \vec{e}_{\theta}= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ 0 & \cos\theta & \sin\theta \\ 0 & -r\sin\theta & r\cos\theta \end{vmatrix}\\ &=\left\langle r, 0, 0\right\rangle \end{aligned} Notice N⃗\vec N points in the positive xx direction as required. We then take the curl of B⃗\vec B: ∇⃗×B⃗=∣ı^ȷ^k^∂x∂y∂zx3y2zy3+yz2∣=ı^(3y2+z2−y2)−ȷ^(0−0)+k^(0−0)=⟨2y2+z2,0,0⟩\begin{aligned} \vec{\nabla}\times\vec{B} &=\begin{vmatrix} \quad\hat{\imath} & \hat{\jmath} & \hat{k} \\[2pt] \quad\partial_x & \partial_y & \partial_z \\[2pt] \quad x^3 & y^2z & y^3+yz^2 \end{vmatrix}\\ &=\hat{\imath}(3y^2+z^2-y^2)-\hat{\jmath}(0-0)+\hat{k}(0-0)\\ &=\left\langle 2y^2+z^2,0,0\right\rangle \end{aligned} Since y=rcos⁡θy=r\cos\theta and z=rsin⁡θz=r\sin\theta, we have ∇⃗×B⃗=⟨2r2cos⁡2θ+r2sin⁡2θ,0,0⟩=⟨r2(cos⁡2θ+1),0,0⟩ \vec\nabla\times\vec B =\left\langle 2r^2\cos^2\theta+r^2\sin^2\theta,0,0\right\rangle =\langle r^2(\cos^2\theta+1),0,0 \rangle The dot product is: ∇⃗×B⃗⋅N⃗=r3(cos⁡2θ+1) \vec\nabla\times\vec B\cdot\vec N=r^3(\cos^2\theta+1) Finally, we compute the surface integral: I=14π∬S∇⃗×B⃗⋅dS⃗=14π∫02π∫02r3(cos⁡2θ+1)drdθ=14π(∫02r3dr)(∫02πcos⁡2θ+1dθ)=1π∫02π1+cos⁡2θ2+1dθ=1π[3θ2+sin⁡2θ4]02π=3ππ=3\begin{aligned} I&=\dfrac{1}{4\pi}\iint_S \vec\nabla\times\vec B\cdot d\vec S =\dfrac{1}{4\pi}\int_0^{2\pi}\int_0^2 r^3(\cos^2\theta+1)\,dr\,d\theta \\ &=\dfrac{1}{4\pi}\left( \int_0^2 r^3 \,dr \right) \left( \int_0^{2\pi} \cos^2\theta+1 \,d\theta\right) \\ &=\dfrac{1}{\pi}\int_0^{2\pi} \dfrac{1+\cos2\theta}{2}+1 \,d\theta =\dfrac{1}{\pi}\left[\dfrac{3\theta}{2} +\dfrac{\sin2\theta}{4}\right]_{0}^{2\pi}=\dfrac{3\pi}{\pi}=3 \end{aligned}

      [×]

    2. the integral version of Ampere's Law.

      Answer

      I=3I=3

      [×]

      Solution

      Ampere's law states that I=14π∮CB⃗⋅ds⃗ I=\dfrac{1}{4\pi}\oint_{C} \vec{B}\cdot d\vec{s} where B⃗\vec B is the magnetic field vector and II is the current through a closed loop CC. We can solve directly, first by parameterizing the boundary of the disk: r⃗(θ)=⟨2,2cos⁡θ,2sin⁡θ⟩ \vec r(\theta)=\langle 2, 2\cos\theta,2\sin\theta \rangle Then, we compute the velocity: v⃗(θ)=⟨0,−2sin⁡θ,2cos⁡θ⟩ \vec v(\theta)=\langle 0, -2\sin\theta,2\cos\theta \rangle We must parametrize B⃗=⟨x3,y2z,y3+yz2⟩\vec B=\langle x^3,y^2z,y^3+yz^2\rangle in terms of this curve: B⃗∣r⃗(θ)=⟨8,8cos⁡2θsin⁡θ,8cos⁡3θ+8cos⁡θsin⁡2θ⟩=⟨8,8cos⁡2θsin⁡θ,8cos⁡θ(cos⁡2θ+sin⁡2θ)⟩=⟨8,8cos⁡2θsin⁡θ,8cos⁡θ⟩\begin{aligned} \left.\vec B\right|_{\vec r(\theta)} &=\langle 8,8\cos^2\theta\sin\theta,8\cos^3\theta+8\cos\theta\sin^2\theta\rangle\\ &=\langle 8,8\cos^2\theta\sin\theta, 8\cos\theta\left(\cos^2\theta+\sin^2\theta\right)\rangle\\ &=\langle 8,8\cos^2\theta\sin\theta,8\cos\theta\rangle \end{aligned} The penultimate step involves taking the dot product of B⃗∣r⃗(θ)\left.\vec B\right|_{\vec r(\theta)} with v⃗\vec v: B⃗∣r⃗(θ)⋅v⃗=0−16cos⁡2θsin⁡2θ+16cos⁡2θ=16cos⁡2θ(1−sin⁡2θ)=16cos⁡4θ\begin{aligned} \left.\vec B\right|_{\vec r(\theta)}\cdot\vec v &=0-16\cos^2\theta\sin^2\theta+16\cos^2\theta\\ &=16\cos^2\theta\left(1-\sin^2\theta\right)=16\cos^4\theta \end{aligned} Finally, we compute the integral: I=14π∮CB⃗⋅ds⃗=14π∫02π16cos⁡4θdθ=14π∫02π16(1+cos⁡2θ2)2dθ=1π∫02π(1+2cos⁡2θ+cos⁡22θ)dθ=1π∫02π1+2cos⁡2θ+1+cos⁡4θ2dθ=1π[3θ2+sin⁡2θ+sin⁡4θ8]02π=3ππ=3\begin{aligned} I&=\dfrac{1}{4\pi}\oint_{C}\vec{B}\cdot d\vec{s} =\dfrac{1}{4\pi}\int_0^{2\pi} 16\cos^4\theta\,d\theta\\ &=\dfrac{1}{4\pi}\int_0^{2\pi}16\left(\dfrac{1+\cos2\theta}{2}\right)^2\,d\theta\\ &=\dfrac{1}{\pi}\int_0^{2\pi}(1+2\cos2\theta+\cos^22\theta)\,d\theta\\ &=\dfrac{1}{\pi}\int_0^{2\pi}1+2\cos2\theta+\dfrac{1+\cos4\theta}{2}\,d\theta\\ &=\dfrac{1}{\pi}\left[\dfrac{3\theta}{2}+\sin{2\theta} +\dfrac{\sin4\theta}{8}\right]_0^{2\pi}=\dfrac{3\pi}{\pi}=3 \end{aligned}

      [×]
    15. PY Checked to here.

    Review Exercises

    xxx

  15. xxx

    Hint

    xxx

    [×]

    Answer

    xxx

    [×]

    Solution

    xxx

    [×]
  16. xxx

    1. xxx

      Answer

      xxx

      [×]

      Solution

      xxx

      [×]

    2. xxx

      Answer

      xxx

      [×]

      Solution

      xxx

      [×]

© 2025 MYMathApps

Supported in part by NSF Grant #1123255