26. Stokes' Theorem
Let \(S\) be a nice surface in \(\mathbb{R}^3\) with a nice properly oriented boundary, \(\partial S\), and let \(\vec{F}\) be a nice vector field on \(S\). Then \[ \iint_S \vec{\nabla}\times\vec{F}\cdot d\vec{S} =\oint_{\partial S} \vec{F}\cdot d\vec{s} \] Each piece of the boundary of the surface must be traversed counterclockwise as seen from the tip of the normal vector to the surface.
d. Applications
4. Surface Independence
We say a vector field \(\vec F\) has surface independent surface integrals if \(\displaystyle \iint_{S_1} \vec F\cdot d\vec S =\iint_{S_2} \vec F\cdot d\vec S\) whenever \(S_1\) and \(S_2\) have the same boundary, i.e. \(\partial S_1=\partial S_2\) with the same orientation.
If \(\vec F\) has a vector potential, then \(\vec F\) has surface independent surface integrals.
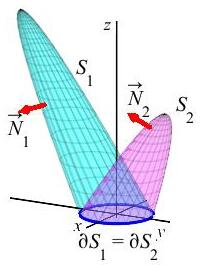
Suppose \(\vec F\) has a vector potential \(\vec A\), i.e. \(\vec F=\vec\nabla\times \vec A\). Then Stokes' Theorem says \[\begin{aligned} \iint_{S_1} \vec{F}\cdot d\vec{S} &=\iint_{S_1} \vec{\nabla}\times\vec{A}\cdot d\vec{S} =\oint_{\partial S_1} \vec{A}\cdot d\vec{S} \\ \iint_{S_2} \vec{F}\cdot d\vec{S} &=\iint_{S_2} \vec{\nabla}\times\vec{A}\cdot d\vec{S} =\oint_{\partial S_2} \vec{A}\cdot d\vec{S} \end{aligned}\] So whenever \(\partial S_1=\partial S_2\), we can conclude: \(\displaystyle \iint_{S_1} \vec{F}\cdot d\vec{S}=\iint_{S_2} \vec{F}\cdot d\vec{S}\). So \(\vec F\) has surface independent surface integrals.
If \(\vec\nabla\cdot\vec F\ne0\), then \(\vec F\) cannot have a vector potential. If \(\vec\nabla\cdot\vec F=0\) and \(\vec F\) is defined in all of \(\mathbb R^3\), then \(\vec F\) has a vector potential. So to know \(\vec F\) has surface independent surface integrals, we do not need to find a vector potential, we only need to show \(\vec\nabla\cdot\vec F=0\).
Compute \(\displaystyle \iint_P \vec{F}\cdot d\vec{S}\) over the paraboloid \(P\) given by \(z=16-x^2-y^2\) for \(z \ge 0\) oriented up and out and the vector field \(\vec F=\langle xz, -yz, x^2+y^2\rangle\).
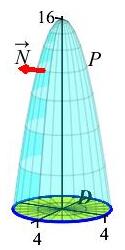
To show \(\vec F\) has a vector potential, compute its divergence \(\vec\nabla\cdot\vec F\).
\(\displaystyle \iint_P \vec{F}\cdot d\vec{S} =128\pi\)
To compute the integral directly, we would need to parametrize the paraboloid, find the normal, evaluate the vector field on the surface, take their dot product and do the integral. That could be hard for the paraboloid. It might be easier on the disk \(D\) given by \(x^2+y^2 \le 16\) with \(z=0\). We check to see if \(\vec F\) has a vector potential, by computing its divergence: \[ \vec\nabla\cdot\vec F=(z)+(-z)+(0)=0 \] So \(\vec F\) has a vector potential and it is surface independent. So we switch to the disk, \(D\). It may be parametrized in cylindrical coordinates as: \[ \vec R=\langle r\cos\theta, r\sin\theta, 0\rangle \] The normal is \(\vec N=\langle 0, 0, r\rangle\), which correctly points up. On the surface, the vector field is: \[\begin{aligned} \vec F&=\langle xz, -yz, x^2+y^2\rangle \\ &=\langle 0, 0, r^2\cos^2\theta+r^2\sin^2\theta\rangle =\langle 0, 0, r^2\rangle \end{aligned}\] The dot product is: \[ \vec F\cdot\vec N=r^3 \] and the integral is \[\begin{aligned} \iint_P &\vec{F}\cdot d\vec{S} =\iint_D \vec{F}\cdot d\vec{S} =\int_0^{2\pi}\int_0^4 \vec{F}\cdot\vec N\,dr\,d\theta \\ &=\int_0^{2\pi}\int_0^4 r^3\,dr\,d\theta =2\pi\left[\dfrac{r^4}{4}\right]_0^4 =128\pi \end{aligned}\]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum