3. Properties of Curves

Exercises

a. Vector Functions, Position, Velocity and Plots

Consider the position vector \(\vec{r}(t)=\langle t,t^2+1\rangle\).
1. Find the position at \(t=3\).
  
  Just substitute \(t=3\) into \(\vec{r}(t)=\langle t,t^2+1\rangle\).
  
  \(\vec{r}(3)=\langle 3,10\rangle\)
2. Find the velocity at \(t=3\).
  
  The velocity is \(\vec{v}(t)=\dfrac{d\vec{r}}{dt}\). Substitute in \(t=3\).
  
  \(\vec{v}(3)=\langle 1,6\rangle\)
  
  The velocity is \(\vec{v}(t)=\dfrac{d\vec r}{dt}=\langle 1,2t\rangle\). At \(t=3\) this is \(\vec{v}(3)=\langle 1,6\rangle\).
  
  lh
3. Plot the parametric curve.
  
  Express \(y\) as a function of \(x\) by setting \(t=x\).
  
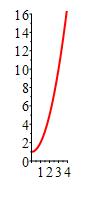
  The coordinate form of the parametric curve is: \[ x=t \qquad y=t^2=1 \] Eliminating the parameter we have \(y=x^2+1\), whose graph is:
  
  lh
4. Add the plot of the position vector at \(t=3\).
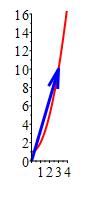
5. Add the plot of the velocity vector at \(t=3\).
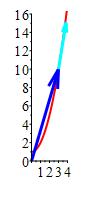
Consider the position vector \(\vec{r}(t) =\langle 2t,3t^2,8t-4\rangle\).
1. Find the position at \(t=3\).
  
  Just substitute \(t=3\) into \(\vec{r}(t)=\langle 2t,3t^2,8t-4\rangle\).
  
  \(\vec{r}(3)=\langle 6,27,20\rangle\)
2. Find the velocity at \(t=3\).
  
  The velocity is \(\vec{v}(t)=\dfrac{d\vec{r}}{dt}\). Substitute in \(t=3\).
  
  \(\vec{v}(3)=\langle 2,18,8\rangle\)
  
  The velocity is \(\vec{v}(t)=\dfrac{d\vec r}{dt}=\langle 2,6t,8\rangle\). At \(t=3\) this is \(\vec{v}(3)=\langle 2,18,8\rangle\).
  
  lh
3. Plot the parametric curve in 3 dimensions.
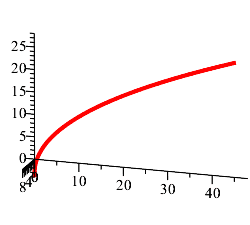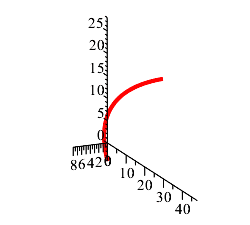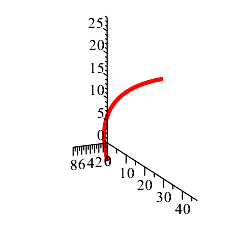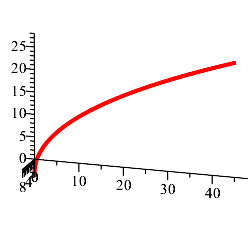
4. Plot the position vector at \(t=3\).
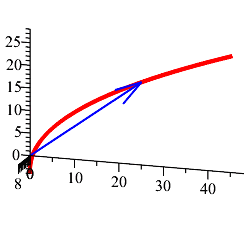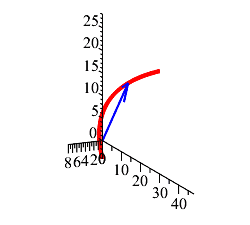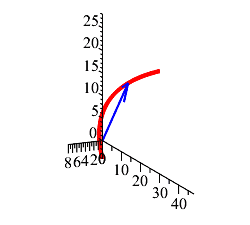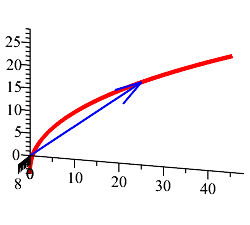
5. Add the plot of the velocity vector at \(t=3\).

b. Limits and Derivatives of Vector Functions

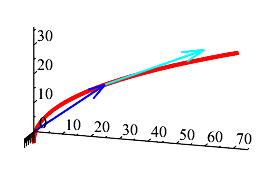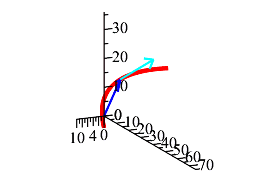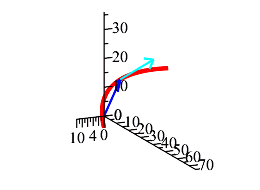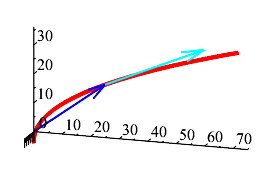
Find the derivative of the vector function \(\vec{f}(t)=\langle 3t-1,2t^{5}+3t+1,6-t\rangle\).

Find the derivative of each component with respect to \(t\)

\(\vec f'(t)=\langle 3,10t^4+3,-1\rangle\)

We find the derivative of \(\vec f(t)\) by differentiating each term: \[\begin{aligned} \vec f'(t)&=\dfrac{d\vec{f}}{dt} =\left\langle \dfrac{df_1}{dt},\dfrac{df_2}{dt},\dfrac{df_3}{dt}\right\rangle \\ &=\dfrac{d}{dt}\langle 3t-1,2t^{5}+3t+1,6-t\rangle =\langle 3,\,10t^4+3,\,-1\rangle \end{aligned}\]

lh,gg
Find the derivative of the vector function \(\vec{g}(t)=\langle -9t,3t^2+5t+4,2t^3+8t^2-6t\rangle\).

\(\vec g'(t)=\langle -9,6t+5,6t^2+16t-6\rangle\)

We find the derivative of \(\vec g(t)\) by differentiating each term: \[\begin{aligned} \vec g'(t) &= \dfrac{d\vec{g}}{dt} =\left\langle \dfrac{dg_1}{dt},\dfrac{dg_2}{dt},\dfrac{dg_3}{dt}\right\rangle \\ &=\dfrac{d}{dt}\langle -9t,3t^2+5t+4,2t^3+8t^2-6t\rangle\\ &=\langle -9,\,6t+5,\,6t^2+16t-6\rangle \end{aligned}\]

lh,gg
Find the derivative of the vector function \(\vec{F}(x)=\langle 2x,x^2+x+1,7-x\rangle\) at the point when \(x=2\).

\(\vec F'(2)=\langle 2,5,-1\rangle\)

We find the derivative of \(\vec F(x)\) by differentiating each term: \[\begin{aligned} \vec F'(x) &=\dfrac{d\vec{F}}{dx} =\left\langle \dfrac{dF_1}{dx},\dfrac{dF_2}{dx},\dfrac{dF_3}{dx}\right\rangle \\ &=\dfrac{d}{dx}\langle 2x,x^2+x+1,7-x\rangle \\ &=\langle 2,2x+1,-1\rangle \end{aligned}\] Evaluating \(\vec F'(x)\) at \(2\): \[ \vec F'(2)=\langle 2,5,-1\rangle \]

lh,gg
Find \(\vec H'(-3)\) if \(\vec{H}(t)=\langle 6,2t^2+t,-4t\rangle\).

\(\vec H'(-3)=\langle 0,-11,-4\rangle\)

We can find the derivative of \(\vec H(t)\) by differentiating term by term: \[\begin{aligned} \vec H'(t) &=\dfrac{d\vec{H}}{dt} =\left\langle \dfrac{dH_1}{dt},\dfrac{dH_2}{dt},\dfrac{dH_3}{dt}\right\rangle \\ &=\dfrac{d}{dt}\langle 6,2t^2+t,-4t\rangle =\langle 0,4t+1,-4\rangle \end{aligned}\] Evaluating \(\vec H'(t)\) at \(-3\): \[ \vec H'(-3)=\langle 0,-11,-4\rangle \]

lh,gg

c. Velocity, Acceleration, and Jerk

Consider the parabola \(y=8-\,\dfrac{1}{2}(x-4)^2\).
1. Find the position vector. (Take \(x=t\).)
  
  \( \vec{r}(t)=\left\langle t,8-\,\dfrac{1}{2}(t-4)^2\right\rangle\)
2. Find the velocity vector.
  
  \( \vec{v}(t)=\langle 1,4-t\rangle \)
  
  To find the velocity vector, we take the derivative of the position vector: \[ \vec{v}(t)=\dfrac{d\vec{r}}{dt} =\left\langle \dfrac{dx}{dt},\dfrac{dy}{dt}\right\rangle =\langle 1,4-t\rangle \]
  
  lh
3. Find the acceleration vector.
  
  \(\vec{a}(t)=\langle 0,-1\rangle\)
  
  We have already found the velocity vector \(\vec{v}(t)=\langle 1,4-t\rangle\) for the parabola. To find the acceleration vector, we take the derivative: \[ \vec{a}(t)=\dfrac{d\vec{v}}{dt}=\langle 0,-1\rangle \]
  
  lh
4. Find the jerk vector.
  
  \(\vec{j}(t)=\langle 0,0\rangle\)
  
  We have already found the acceleration vector \(\vec{a}(t)=\langle 0,-1\rangle\) for the parabola. To find the jerk vector, we take the derivative: \[ \vec{j}(t)=\dfrac{d\vec{a}}{dt}=\langle 0,0\rangle \]
  
  lh
5. Plot the original parabola from \(t=0\) to \(t=8\). At three different points along the curve, plot the curve's corresponding velocity and acceleration vectors.
  
  The plot shows the parabola along with its corresponding velocity and acceleration vectors at \(7\) points.
  
  Note that the acceleration is a constant vector on the curve which points straight down (like gravity). This means the velocity is always bending down: an object that followed along this curve would be decelerating on the way up and accelerating on the way down.
  
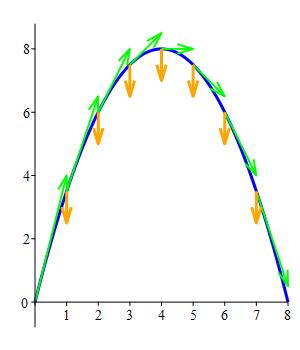
  \(\vec{r}(t)\) is Blue,
  \(\vec{v}(t)\) is Green,
  \(\vec{a}(t)\) is Orange.
Consider the position vector \(\vec{r}(t)= \langle t^3+2t^2+t,t-3,t^4+6\rangle\).
1. Find the velocity vector.
  
  \(\vec{v}(t)=\dfrac{d\vec{r}}{dt} =\left\langle \dfrac{dr_{1}}{dt},\dfrac{dr_{2}}{dt}, \dfrac{dr_{3}}{dt}\right\rangle\)
  
  \(\vec{v}(t)=\langle 3t^2+4t+1,1,4t^3\rangle\)
  
  Recall that velocity is the derivative of position. So: \[\begin{aligned} \vec{v}(t)&=\dfrac{d\vec{r}}{dt} =\left\langle \dfrac{dr_{1}}{dt},\dfrac{dr_{2}}{dt}, \dfrac{dr_{3}}{dt} \right\rangle \\ &=\dfrac{d}{dt}\langle t^3+2t^2+t,t-3,t^4+6\rangle \\ &=\langle 3t^2+4t+1,1,4t^3\rangle \end{aligned}\]
  
  lh
2. Find the acceleration vector.
  
  \(\vec{a}(t)=\dfrac{d\vec{v}}{dt} =\left\langle \dfrac{dv_{1}}{dt},\dfrac{dv_{2}}{dt}, \dfrac{dv_{3}}{dt} \right\rangle\)
  
  \(\vec{a}(t)=\langle 6t+4,0,12t^2\rangle \)
  
  Recall that acceleration is the derivative of velocity. So: \[\begin{aligned} \vec{a}(t)=\dfrac{d\vec v}{dt} &=\left\langle \dfrac{dv_{1}}{dt},\dfrac{dv_{2}}{dt}, \dfrac{dv_{3}}{dt} \right\rangle \\ &=\dfrac{d}{dt}\langle 3t^2+4t+1,1,4t^3\rangle \\ &=\langle 6t+4,0,12t^2\rangle \end{aligned}\]
  
  lh
3. Find the jerk vector.
  
  \(\vec{j}(t)=\dfrac{d\vec{a}}{dt}= \left\langle \dfrac{da_{1}}{dt}, \dfrac{da_{2}}{dt},\dfrac{da_{3}}{dt}\right\rangle\)
  
  \(\vec{j}(t)=\langle 6,0,24t\rangle\)
  
  Recall that jerk is the derivative of acceleration. So: \[\begin{aligned} \vec{j}(t)=\dfrac{d\vec{a}}{dt} &=\left\langle \dfrac{da_{1}}{dt},\dfrac{da_{2}}{dt}, \dfrac{da_{3}}{dt}\right\rangle \\ &=\dfrac{d}{dt}\langle 6t+4,0,12t^2\rangle \\ &=\langle 6,0,24t\rangle \end{aligned}\]
  
  lh
Consider the position vector \(\vec{r}(t) =\left\langle e^{t/2},t^{5/2}+1,\sin t\right\rangle\).
1. Find the velocity vector.
  
  \(\vec{v}(t) =\left\langle \dfrac{1}{2}e^{t/2}, \dfrac{5}{2}t^{3/2},\cos t\right\rangle\)
  
  Recall that velocity is the derivative of position. So: \[\begin{aligned} \vec{v}(t)&=\dfrac{d\vec{r}}{dt} =\left\langle \dfrac{dr_{1}}{dt},\dfrac{dr_{2}}{dt}, \dfrac{dr_{3}}{dt}\right\rangle \\ &=\dfrac{d}{dt}\left\langle e^{t/2} ,t^{5/2}+1,\sin t \right\rangle \\ &=\left\langle \dfrac{1}{2}e^{t/2}, \dfrac{5}{2}t^{3/2},\cos t\right\rangle \end{aligned}\]
  
  lh
2. Find the acceleration vector.
  
  \(\vec{a}(t) =\left\langle \dfrac{1}{4}e^{t/2}, \dfrac{15}{4}t^{1/2},-\sin t\right\rangle\)
  
  Recall that acceleration is the derivative of velocity. So: \[\begin{aligned} \vec{a}(t)&=\dfrac{d\vec v}{dt} =\left\langle \dfrac{dv_{1}}{dt},\dfrac{dv_{2}}{dt}, \dfrac{dv_{3}}{dt}\right\rangle \\ &=\dfrac{d}{dt}\left\langle \dfrac{1}{2}e^{t/2}, \dfrac{5}{2}t^{3/2},\cos t\right\rangle \\ &=\left\langle \dfrac{1}{4}e^{t/2}, \dfrac{15}{4}t^{1/2},-\sin t\right\rangle \end{aligned}\]
  
  lh
3. Find the jerk vector.
  
  \(\vec{j}(t)=\left\langle \dfrac{1}{8}e^{t/2}, \dfrac{15}{8}t^{-1/2},-\cos t\right\rangle\)
  
  Recall that jerk is the derivative of acceleration. So: \[\begin{aligned} \vec{j}(t)&=\dfrac{d\vec{a}}{dt} =\left\langle \dfrac{da_{1}}{dt},\dfrac{da_{2}}{dt}, \dfrac{da_{3}}{dt}\right\rangle \\ &=\dfrac{d}{dt}\left\langle \dfrac{1}{4}e^{t/2}, \dfrac{15}{4}t^{1/2},-\sin t\right\rangle \\ &=\left\langle \dfrac{1}{8}e^{t/2}, \dfrac{15}{8}t^{-1/2},-\cos t\right\rangle \end{aligned}\]
  
  lh
Find the tangent vector to the curve \(\vec{r}(t)=\langle 4t+5,2t^2-2,7\rangle\) at \(t=3\).

Which vector (position, velocity, or acceleration) lies tangent to the curve?

\(\vec{v}(3)=\langle 4,12,0\rangle\)

The tangent vector to the curve \(\vec r(t)\) is \(\vec v(t)\). \[\begin{aligned} \vec{v}(t)&=\dfrac{d\vec{r}}{dt} =\left\langle \dfrac{dr_{1}}{dt},\dfrac{dr_{2}}{dt}, \dfrac{dr_{3}}{dt}\right\rangle \\ &= \dfrac{d}{dt}\langle 4t+5,2t^2-2,7\rangle \\ &=\langle 4,4t,0\rangle \end{aligned}\] Substituting \(3\) into \(\vec{v}\): \[\begin{aligned} \vec{v}(3)=\langle 4,12,0\rangle \end{aligned}\]

lh

d. Arc Length, Arc Length Parameter, and Speed

Find the length of the curve \(\vec{r}(t)=\langle 3t+32,4t+1,-12t-1\rangle\) from \(t=-2\) to \(t=4\).

\(\displaystyle L=\int_{a}^{b} |\vec{v}|\,dt\)

\(L=78\)

Recall the formula for arc length: \[ L=\int_A^B\,ds=\int_a^b |\vec{v}|\,dt \] So first we must find \(|\vec{v}|\): \[ \vec v(t) =\langle 3,4,-12\rangle \qquad |\vec v|=\sqrt{3^2+4^2+12^2}=13 \] Substituting and solving the integral: \[\begin{aligned} L&=\int_{a}^{b} |\vec{v}|\,dt =\int_{-2}^4 13\,dt \\ &=13(4-(-2))=78 \\ \end{aligned}\]

lh
Find the length of the curve \(\vec{r}(t)=\langle\sin t,-\cos t,3t+2\rangle\) from \( t=0\) to \(t=\dfrac{\pi}{2}\).

\(L=\dfrac{\pi\sqrt{10}}{2}\approx 4.97\)

Recall the formula for arc length: \[ L=\int_A^B\,ds=\int_a^b |\vec{v}|\,dt \] So first we must find \(|\vec{v}|\): \[ \vec v(t) =\langle \cos t,\sin t,3\rangle \qquad |\vec v|=\sqrt{\cos^2 t+\sin^2 t+3^2}=\sqrt{10} \] Substituting and computing the integral: \[\begin{aligned} L&=\int_{a}^{b} |\vec{v}|\,dt =\int_0^{\pi/2} \sqrt{10}\,dt \\ &=\sqrt{10}\left(\dfrac{\pi}{2}-0\right) =\dfrac{\pi\sqrt{10}}{2}\approx 4.97 \end{aligned}\]

lh
Reparametrize \(\vec{r}(t)=\langle 3t+7,4\sin t-5,4\cos t-1\rangle\) with respect to arc length, \(s\), starting from \(t=0\).

To reparametrize \(\vec{r}(t)\) with respect to arc length \(s\) starting from \(t=0\), solve for \(s\) in terms of \(t\) using \(\displaystyle s(t)=\int_0^t |\vec{v}|\,dt\). Then solve for \(t(s)\), and plug \(t(s)\) into \(\vec{r}(t)\).

\(\vec r(s) =\left\langle 3\left(\dfrac{s}{5}\right)+7, 4\sin\left(\dfrac{s}{5}\right)-5, 4\cos\left(\dfrac{s}{5}\right)-1\right\rangle\)

We can use the arclength fromula to find \(s(t)\): \[ s(t)=\int_0^t |\vec{v}|\,dt \] So first we must find \(|\vec{v}|\): \[\begin{aligned} \vec v(t)&=\langle 3,4\cos t,-4\sin t\rangle \\ |\vec v(t)|&=\sqrt{3^2+4^2\cos^2 t+4^2\sin^2 t}=\sqrt{9+16}=5 \end{aligned}\] Computing \(s(t)\): \[ s(t)=\int_0^t |\vec{v}|\,dt=\int_0^{t} 5\,dt=5t \] So \(t=\dfrac{s}{5}\) and: \[ \vec r(s) =\left\langle \dfrac{3s}{5}+7, 4\sin\left(\dfrac{s}{5}\right)-5, 4\cos\left(\dfrac{s}{5}\right)-1\right\rangle \]

lh
Find the speed of the position vector \(\vec{r} (t)=\langle 3t^2+2,2t^3-5t,9t-2\rangle\) at \(t=1\).

\(\text{speed}(t)=|\vec v(t)|\)

\(\text{speed}(1)=\sqrt{118}\approx 10.9\)

Speed is the derivative of arclength, which is \(|\vec{v}|\). So first we find \(\vec{v}(1)\): \[\begin{aligned} \vec{v}(t)&=\langle 6t,6t^2-5,9\rangle \\ \vec{v}(1)&=\langle 6,1,9\rangle \\ \end{aligned}\] Next we find \(|\vec{v}(1)|\) which is equivalent to the speed at \(t=1\): \[\begin{aligned} \text{speed}(1)=|\vec{v}(1)|=\sqrt{6^2+1^2+9^2}=\sqrt{118}\approx 10.9 \end{aligned}\]

lh

For the parametric curve \(\vec r(t)=\left\langle2t^{1/2},\sqrt{6}t,2t^{3/2}\right\rangle\) find the arc length between \(t=1\) and \(t=4\).

In finding the speed, the quantity inside the square root is a perfect square.

\(L=16\)

Since the position is: \[\vec{r}=\left\langle2t^{1/2},\sqrt{6}t,2t^{3/2}\right\rangle\] the velocity is: \[\vec{v}=\left\langle t^{-1/2},\sqrt{6},3t^{1/2}\right\rangle\] Therefore, the speed is: \[\begin{aligned} |\vec{v}|&=\sqrt{t^{-1}+6+9t} =\sqrt{(t^{-1/2}+3t^{1/2})^2} \\ &=t^{-1/2}+3t^{1/2} \end{aligned}\] To find the arc length, we take the integral of the speed between \(t=1\) and \(t=4\). \[ \begin{aligned} L&=\int_1^4\left|\vec v\right| dt =\int_1^4\left(t^{-1/2}+3t^{1/2}\right) dt \\ &=\left[2t^{1/2}+2t^{3/2}\right]_1^4 =(4+16)-(2+2)=16 \end{aligned} \]

ad

e. Tangent, Normal, and Binormal Vectors

For the parametric curve \(\vec r(t)=\left\langle2t^{1/2},\sqrt{6}t,2t^{3/2}\right\rangle\) find \(\hat T\), \(\hat N\) and \(\hat B\).

The tangent vector is \(\hat T=\dfrac{\vec v}{|\vec v|}\).

The binormal vector is \(\hat B=\dfrac{\vec v\times\vec a}{|\vec v\times\vec a|}\).

Finally, the normal vector is \(\hat N=\vec B\times\vec T\).

\(\hat T =\dfrac{\vec{v}}{|\vec{v}|} =\dfrac{1}{3t+1}\left\langle 1,\sqrt{6}t^{1/2},3t\right\rangle\)
\(\hat N =\dfrac{1}{3t+1}\left\langle-\sqrt{6}t^{1/2},1-3t, \sqrt{6}t^{1/2}\right\rangle\)
\(\hat B =\dfrac{1}{3t+1}\left\langle 3t,-\sqrt{6}t^{1/2},1\right\rangle\)

From a previous problem, the velocity is: \[\vec{v}=\left\langle t^{-1/2},\sqrt{6},3t^{1/2}\right\rangle\] and its length is: \[\begin{aligned} |\vec{v}|&=t^{-1/2}+3t^{1/2}=\dfrac{3t+1}{t^{1/2}} \end{aligned}\] Therefore, the unit tangent vector is: \[\begin{aligned} \hat T&=\dfrac{\vec v}{|\vec v|} =\dfrac{t^{1/2}}{3t+1}\left\langle t^{-1/2},\sqrt{6},3t^{1/2}\right\rangle \\ &=\dfrac{1}{3t+1}\left\langle 1,\sqrt{6}t^{1/2},3t\right\rangle \end{aligned}\] To find the binormal, we need \(\vec v\times\vec a\) and its length. The acceleration is: \[ \vec{a}=\left\langle -\dfrac{1}{2}t^{-3/2},0,\dfrac{3}{2}t^{-1/2}\right\rangle \] So: \[\begin{aligned} \vec v\times\vec a &=\begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ t^{-1/2} & \sqrt{6} & 3t^{1/2} \\ -\dfrac{1}{2}t^{-3/2} & 0 & \dfrac{3}{2}t^{-1/2} \end{vmatrix} \\ &=\hat\imath\left(\dfrac{3}{2}\sqrt{6}t^{-1/2}\right) -\hat\jmath\left(\dfrac{3}{2}t^{-1}--\dfrac{3}{2}t^{-1}\right) +\hat k\left(\dfrac{1}{2}\sqrt{6}t^{-3/2}\right) \\ &=\left\langle\dfrac{3}{2}\sqrt{6}t^{-1/2},-3t^{-1}, \dfrac{1}{2}\sqrt{6}t^{-3/2}\right\rangle \\ \end{aligned}\] \[\begin{aligned} |\vec v\times\vec a| &=\sqrt{\left(\dfrac{3}{2}\sqrt{6}t^{-1/2}\right)^2+(-3t^{-1})^2 +\left(\dfrac{1}{2}\sqrt{6}t^{-3/2}\right)^2} \\ &=\sqrt{\dfrac{27}{2}t^{-1}+9t^{-2}+\dfrac{3}{2}t^{-3}} \\ &=\dfrac{\sqrt{6}}{2t^{3/2}}\sqrt{9t^2+6t+1} \\ &=\dfrac{\sqrt{6}(3t+1)}{2t^{3/2}} \end{aligned}\] Therefore, the unit binormal vector is: \[ \begin{aligned} \hat B &=\dfrac{\vec v\times\vec a}{|\vec v\times\vec a|} \\ &=\dfrac{2t^{3/2}}{\sqrt{6}(3t+1)}\left\langle\dfrac{3}{2}\sqrt{6}t^{-1/2},-3t^{-1},\dfrac{1}{2}\sqrt{6}t^{-3/2}\right\rangle \\ &=\dfrac{1}{3t+1}\left\langle 3t,-\sqrt{6}t^{1/2},1 \right\rangle \end{aligned} \] Finally, the unit normal vector is: \[\begin{aligned} \hat N&=\hat B\times\hat T=\dfrac{1}{(3t+1)^2} \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 3t & -\sqrt{6}t^{1/2} & 1 \\ 1 & \sqrt{6}t^{1/2} & 3t \end{vmatrix} \\ &=\dfrac{1}{(3t+1)^2}\left[ \hat\imath\left(-3\sqrt{6}t^{3/2}-\sqrt{6}t^{1/2}\right) -\hat\jmath\left(9t^2-1\right) +\hat k\left(3\sqrt{6}t^{3/2}+\sqrt{6}t^{1/2}\right) \right] \\ &=\dfrac{1}{(3t+1)^2}\left\langle -\sqrt{6}t^{1/2}(3t+1),(1-3t)(1+3t), \sqrt{6}t^{1/2}(3t+1)\right\rangle \\ &=\dfrac{1}{3t+1}\left\langle -\sqrt{6}t^{1/2},1-3t,\sqrt{6}t^{1/2}\right\rangle \end{aligned}\]

ad,gg

To see \(\hat T\), \(\hat N\), and \(\hat B\) are orthogonal, we check their dot products are zero: \[\begin{aligned} \hat T\cdot\hat N &=\dfrac{1}{(3t+1)^2}\left\langle 1,\sqrt{6}t^{1/2},3t \right\rangle \cdot\left\langle -\sqrt{6}t^{1/2}, 1-3t ,\sqrt{6}t^{1/2}\right\rangle \\ &=\dfrac{-\sqrt{6}t^{1/2}+\sqrt{6}t^{1/2}(1-3t)+3t\sqrt{6}t^{1/2}}{(3t+1)^2} \\ &=\dfrac{-\sqrt{6}t^{1/2}+\sqrt{6}t^{1/2}-3t\sqrt{6}t^{1/2}+3t\sqrt{6}t^{1/2}}{(3t+1)^2} =0 \\ \hat N\cdot\hat B &=\dfrac{1}{(3t+1)^2}\left\langle -\sqrt{6}t^{1/2},1-3t,\sqrt{6}t^{1/2}\right\rangle \cdot\left\langle 3t,-\sqrt{6}t^{1/2},1\right\rangle \\ &=\dfrac{-\sqrt{6}t^{1/2}3t-(1-3t)\sqrt{6}t^{1/2}+\sqrt{6}t^{1/2}}{(3t+1)^2} \\ &=\dfrac{-3\sqrt{6}t^{3/2}-\sqrt{6}t^{1/2}+3\sqrt{6}t^{3/2}+\sqrt{6}t^{1/2}}{(3t+1)^2} =0 \\ \hat B\cdot\hat T &=\dfrac{1}{(3t+1)^2}\left\langle 3t,-\sqrt{6}t^{1/2},1\right\rangle \cdot\left\langle 1,\sqrt{6}t^{1/2},3t\right\rangle \\ &=\dfrac{3t-6t+3t}{(3t+1)^2}=0 \end{aligned}\]
Find the unit tangent vector of the position vector \(\vec{r}(t)=\left\langle t+2,\sqrt{\dfrac{5}{2}}(t^2-4),\dfrac{5}{3}t^3+3\right\rangle\) at:
1. a general value of \(t\).
  
  The unit tangent vector is \(\hat{T}=\dfrac{\vec{v}}{|\vec{v}|}\).
  
  \(\hat{T} =\dfrac{1}{1+5t^2}\left\langle 1,\sqrt{10}t,5t^2 \right\rangle\)
  
  Since the position is: \[\vec{r}=\left\langle t+2,\sqrt{\dfrac{5}{2}}(t^2-4),\dfrac{5}{3}t^3+3\right\rangle\] the velocity is: \[\vec{v}=\left\langle 1,\sqrt{10}t,5t^2 \right\rangle\] and the speed is: \[\begin{aligned} |\vec{v}|&=\sqrt{1^2+\left(\sqrt{10}t\right)^2+(5t^2)^2} \\ &=\sqrt{1+10t^2+25t^4} \\ &=\sqrt{(1+5t^2)^2} \\ &=1+5t^2 \end{aligned}\] Therefore, the unit tangent vector is: \[\begin{aligned} \hat T&=\dfrac{\vec v}{|\vec v|} \\ &=\dfrac{1}{1+5t^2}\left\langle 1,\sqrt{10}t,5t^2 \right\rangle \end{aligned}\]
  
  lh,ad
2. \(t=1\).
  
  \(\hat{T} =\left\langle\dfrac{1}{6},\dfrac{\sqrt{10}}{6},\dfrac{5}{6}\right\rangle\)
  
  From part (a), we found: \[ \hat T =\dfrac{1}{1+5t^2}\left\langle 1,\sqrt{10}t,5t^2 \right\rangle \] Plugging \(t=1\), we get: \[ \hat T=\dfrac{1}{1+5}\left\langle 1,\sqrt{10},5 \right\rangle =\left\langle\dfrac{1}{6},\dfrac{\sqrt{10}}{6},\dfrac{5}{6}\right\rangle \]
  
  lh,ad
Find the binormal vector of the curve \(\vec{r} (t)=\langle 3t+2,3t^2+5,2t^3+4\rangle\) at:
1. a general value of \(t\).
  
  The unit binormal vector is \(\hat{B} =\dfrac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}\)
  
  \(\hat{B}=\dfrac{1}{2t^2+1}\langle 2t^2,-2t,1\rangle\)
  
  We know that the binormal is: \[ \hat{B}=\dfrac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|} \] So we need to know \(\vec{v}\times\vec{a}\) and its length. Since the position is: \[ \vec{r}=\langle 3t+2,3t^2+5,2t^3+4\rangle \] The velocity is: \[ \vec{v}=\langle 3,6t,6t^2\rangle \] And the acceleration is: \[ \vec{a}=\langle 0,6,12t\rangle \] So, \(\vec{v}\times\vec{a}\) is: \[\begin{aligned} \vec{v}\times\vec{a}&= \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 3 & 6t & 6t^2 \\ 0 & 6 & 12t \end{vmatrix} =\hat\imath(72t^2-36t^2)-\hat\jmath(36t-0)+\hat k(18-0) \\ &=\langle 36t^2,-36t,18\rangle \end{aligned}\] and its length is: \[\begin{aligned} |\vec{v}\times\vec{a}| &=\sqrt{(36t^2)^2+(36t)^2+18^2} =\sqrt{(36t^2)^2+2\cdot36t^2\cdot18+18^2} \\ &=36t^2+18 \\ \end{aligned}\] So, the unit binormal vector is: \[\begin{aligned} \hat{B}&=\dfrac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}\\ &=\dfrac{1}{36t^2+18}\langle 36t^2,-36t,18\rangle =\dfrac{1}{2t^2+1}\langle 2t^2,-2t,1\rangle \\ \end{aligned}\]
  
  lh,ad
2. \(t=2\).
  
  \(\hat{B}=\left\langle \dfrac{8}{9},-\,\dfrac{4}{9},\dfrac{1}{9}\right\rangle\)
  
  Plugging \(t=2\) into \(\hat{B}=\dfrac{1}{2t^2+1}\langle 2t^2,-2t,1\rangle\), we get: \[\hat{B}=\dfrac{1}{9}\langle 8,-4,1\rangle =\left\langle \dfrac{8}{9},-\,\dfrac{4}{9},\dfrac{1}{9}\right\rangle\]
  
  lh,ad
Find the normal vector of the curve \(\vec{r}(t)=\left\langle 2t+4,2t^2+11,\dfrac{4}{3}t^3\right\rangle\) at:
1. a general value of \(t\).
  
  The unit normal vector is \(\hat{N}=\hat{B}\times\hat{T}\).
  
  \(\hat{N} =\dfrac{1}{2t^2+1}\langle -2t,1-2t^2,2t\rangle\)
  
  We know that the unit normal vector is: \[ \hat{N}=\hat{B}\times\hat{T} \] So we need \(\hat{T}\) and \(\hat{B}\), which means we need \(\vec{v}\), \(\vec{v}\times\vec{a}\) and their lengths. Since the position is: \[ \vec{r}=\left\langle 2t+4,2t^2+11,\dfrac{4}{3}t^3\right\rangle \] The velocity is: \[ \vec{v}=\langle 2,4t,4t^2\rangle \] And the acceleration is: \[ \vec{a}=\langle 0,4,8t\rangle \] So the speed is: \[\begin{aligned} |\vec{v}|&=\sqrt{4+16t^2+16t^4} \\ &=\sqrt{(2+4t^2)^2}=2+4t^2 \end{aligned}\] Therefore, the unit tangent vector is: \[ \hat{T}=\dfrac{\vec{v}}{|\vec{v}|}=\dfrac{1}{2+4t^2}\langle 2,4t,4t^2\rangle =\dfrac{1}{1+2t^2}\langle 1,2t,2t^2\rangle \] To find \(\hat{B}\), we need \(\vec{v}\times\vec{a}\) and its length. So \(\vec{v}\times\vec{a}\) is: \[\begin{aligned} \vec{v}\times\vec{a}&= \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 2 & 4t & 4t^2 \\ 0 & 4 & 8t \end{vmatrix} \\ &=\hat\imath(32t^2-16t^2)-\hat\jmath(16t)+\hat k(8) \\ &=\langle 16t^2,-16t,8\rangle \end{aligned}\] And its length is: \[\begin{aligned} |\vec{v}\times\vec{a}|&=\sqrt{(16t^2)^2+(16t)^2+8^2} \\ &=\sqrt{(16t^2+8)^2}=16t^2+8 \end{aligned}\] Therefore, the unit binormal vector is: \[\begin{aligned} \hat{B}&=\dfrac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|} \\ &=\dfrac{1}{16t^2+8}\langle 16t^2,-16t,8\rangle =\dfrac{1}{2t^2+1}\langle 2t^2,-2t,1\rangle \end{aligned}\] Finally, the unit normal is: \[\begin{aligned} \hat{N}&=\hat{B}\times\hat{T} =\dfrac{1}{(2t^2+1)^2} \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 2t^2 & -2t & 1 \\ 1 & 2t & 2t^2 \end{vmatrix} \\ &=\dfrac{1}{(2t^2+1)^2}\left[\rule{0pt}{10pt}\hat\imath(-4t^3-2t)-\hat\jmath(4t^4-1)\right. \\ &\qquad\qquad\qquad\left.\rule{0pt}{10pt}+\hat k(4t^3+2t)\right] \\ &=\dfrac{1}{(2t^2+1)^2}\left[\rule{0pt}{10pt}\hat\imath(-2t)(2t^2+1)-\hat\jmath(2t^2-1)(2t^2+1)\right. \\ &\qquad\qquad\qquad\left.\rule{0pt}{10pt}+\hat k(2t)(2t^2+1)\right] \\ &=\dfrac{1}{2t^2+1}\langle -2t,1-2t^2,2t\rangle \\ \end{aligned}\]
  
  lh,ad,gg
  
  We check that \(\hat{T}\), \(\hat{N}\) and \(\hat{B}\) are mutually perpendicular unit vectors. \[\begin{aligned} \hat{T}\cdot\hat{T} &=\dfrac{1}{(2t^2+1)^2}\langle 1,2t,2t^2\rangle\cdot\langle 1,2t,2t^2\rangle \\ &=\dfrac{1}{(2t^2+1)^2}\left(1+4t^2+4t^4\right) =1 \\ \hat{N}\cdot\hat{N} &=\dfrac{1}{(2t^2+1)^2}\langle -2t,1-2t^2,2t\rangle\cdot\langle -2t,1-2t^2,2t\rangle \\ &=\dfrac{1}{(2t^2+1)^2}\left(4t^2+(1-2t^2)^2+4t^2\right) \\ &=\dfrac{1}{(2t^2+1)^2}\left(8t^2+1-4t^2+4t^4\right) =1 \\ \hat{B}\cdot\hat{B} &=\dfrac{1}{(2t^2+1)^2}\langle 2t^2,-2t,1\rangle\cdot\langle 2t^2,-2t,1\rangle \\ &=\dfrac{1}{(2t^2+1)^2}\left(4t^4+4t^2+1\right) =1 \end{aligned}\] \[\begin{aligned} \hat{T}\cdot\hat{N} &=\dfrac{1}{(2t^2+1)^2}\langle 1,2t,2t^2\rangle\cdot\langle -2t,1-2t^2,2t\rangle \\ &=\dfrac{1}{(2t^2+1)^2}\left(-2t+2t-4t^3+4t^3\right) =0 \\ \hat{T}\cdot\hat{B} &=\dfrac{1}{(2t^2+1)^2}\langle 1,2t,2t^2\rangle\dot\langle 2t^2,-2t,1\rangle \\ &=\dfrac{1}{(2t^2+1)^2}\left(2t^2-4t^2+2t^2\right) =0 \\ \hat{N}\cdot\hat{B} &=\dfrac{1}{(2t^2+1)^2}\langle -2t,1-2t^2,2t\rangle\cdot\langle 2t^2,-2t,1\rangle \\ &=\dfrac{1}{(2t^2+1)^2}\left(-4t^3-2t(1-2t^2)+2t\right) =0 \end{aligned}\]
2. \(t=2\).
  
  \(\hat{N}=\left\langle-\,\dfrac{4}{9},\dfrac{7}{9},\dfrac{4}{9}\right\rangle\)
  
  Plugging \(t=2\) into \(\hat{N}=\dfrac{1}{2t^2+1}\langle -2t,1-2t^2,2t\rangle\), we get: \[ \hat{N}=\dfrac{1}{9}\left\langle -4,-7,4\right\rangle =\left\langle-\,\dfrac{4}{9},-\,\dfrac{7}{9},\dfrac{4}{9}\right\rangle \]
  
  lh,ad

f. Curvature and Torsion

Find the curvature \(\kappa\) for the curve \(\vec{r}(t)=\langle 3t^4,3t^2+5,4t^3+3 \rangle\)
1. for a general value of \(t\).
  
  \(\kappa=\dfrac{|\vec{v}\times\vec{a}|}{|\vec{v}|^3}\)
  
  \(\kappa =\dfrac{1}{3t(1+2t^2)^2}\)
  
  We want to find the curvature, \(\kappa =\dfrac{|\vec{v}\times\vec{a}|}{|\vec{v}|^3}\). Since the position is \(\vec{r}(t)=(3t^4,3t^2+5,4t^3+3)\), the velocity, speed and acceleration are: \[\begin{aligned} \vec{v}&=\langle 12t^3,6t,12t^2 \rangle \\ |\vec{v}|&=\sqrt{144t^6+36t^2+144t^4} \\ &=6t\sqrt{4t^4+1+4t^2} =6t(1+2t^2) \\ \vec{a}&=\langle 36t^2,6,24t \rangle \\ \end{aligned}\] Then the cross product of the velocity and acceleration and its length are: \[\begin{aligned} \vec{v}\times\vec{a}&= \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 12t^3 & 6t & 12t^2 \\ 36t^2 & 6 & 24t \end{vmatrix} \\ &=\hat\imath(144t^2-72t^2)-\hat\jmath(288t^4-432t^4)+ \hat k(72t^3-216t^3) \\ &=\langle 72t^2,144t^4,-144t^3 \rangle \\ &=72t^2\langle 1,2t^2,-2t \rangle \\ |\vec{v}\times\vec{a}| &=72t^2\sqrt{1+4t^4+4t^2}\\ &=72t^2(1+2t^2) \end{aligned}\] So the curvature is: \[ \kappa =\dfrac{|\vec{v}\times\vec{a}|}{|\vec{v}|^3} =\dfrac{72t^2(1+2t^2)}{[6t(1+2t^2)]^3} =\dfrac{1}{3t(1+2t^2)^2} \]
  
  lh,gg
2. at \(t=1\).
  
  At \(t=1\), \(\kappa=\dfrac{1}{27}\).
  
  We plug \(t=1\) into \[\kappa =\dfrac{1}{3t(1+2t^2)^2}\] to get \[\kappa =\dfrac{1}{3(1+2(1)^2)^2}= \dfrac{1}{27}\]
  
  lh,gg
Find the torsion \(\tau\) for the curve in the previous problem
1. for a general value of \(t\).
  
  \(\tau =\dfrac{\vec{v}\times\vec{a}\cdot\vec{j}}{|\vec{v}\times\vec{a}|^2}\)
  
  \(\tau=\dfrac{1}{3t(1+2t^2)^2}\)
  
  We want to find the torsion, \(\tau =\dfrac{\vec{v}\times\vec{a}\cdot\vec{j}}{|\vec{v}\times\vec{a}|^2}\). In the previous problem we found: \[\begin{aligned} \vec{v}&=\langle 12t^3,6t,12t^2 \rangle \\ \vec{a}&=\langle 36t^2,6,24t \rangle \\ \vec{v}\times\vec{a} &=72t^2\langle 1,2t^2,-2t \rangle \\ |\vec{v}\times\vec{a}| &= 72t^2(1+2t^2) \end{aligned}\] So we compute: \[\begin{aligned} \vec{j}&=\langle 72t,0,24\rangle \\ \vec{v}\times\vec{a}\cdot\vec{j} &= 72t^2\langle 1,2t^2,-2t \rangle \cdot \langle 72t,0,24\rangle \\ &= 72t^2(72t - 48t) = 1728t^3 \end{aligned}\] Consequently, the torsion is: \[\begin{aligned} \tau &=\dfrac{\vec{v}\times\vec{a}\cdot\vec{j}}{|\vec{v}\times\vec{a}|^2} =\dfrac{1728t^3}{[72t^2(1+2t^2)]^2} \\ &=\dfrac{1728t^3}{5184t^4(1+2t^2)^2} =\dfrac{1}{3t(1+2t^2)^2} \end{aligned}\]
  
  lh,gg
2. at \(t=1\).
  
  At \(t=1\), \(\tau=\dfrac{1}{27}\)
  
  We plug in \(t=1\) into \[\tau=\dfrac{1}{3t(1+2t^2)^2}\] to get \[\tau=\dfrac{1}{3(3)^2} = \dfrac{1}{27}\]
  
  lh,gg

g. Tangential and Normal Acceleration

Find the tangential and normal acceleration to the curve \(\vec{r}(t) =\left\langle \dfrac{1}{3}t^3+5,2t+1,t^2-3\right\rangle\)
1. for a general value of \(t\).
  
  \(a_{T}=\dfrac{d}{dt}|\vec{v}|\)
  \(a_{N}=\kappa |\vec v|^2\)
  
  \(a_{T}=2t\)
  \(a_{N}=2\)
  
  To find the tangential acceleration we use \(a_{T}=\dfrac{d|\vec{v}|}{dt}\): \[\begin{aligned} \vec{v}&=\langle t^2,2,2t \rangle \\ |\vec{v}|&=\sqrt{t^4+4+4t^2}=\sqrt{(t^2+2)^2}=t^2+2 \end{aligned}\] So the tangential acceleration is: \[ a_{T}=\dfrac{d|\vec{v}|}{dt}=2t \] To find the normal acceleration we will use: \[a_{N} = \kappa |\vec v|^2 = \dfrac{|\vec{v}\times\vec{a}|}{|\vec v|^3}|\vec v|^2 = \dfrac{|\vec{v}\times\vec{a}|}{|\vec v|}\] First, we find \(|\vec{v}\times\vec{a}|\): \[\begin{aligned} \vec{v}\times\vec{a}&= \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ t^2 & 2 & 2t \\ 2t & 0 & 2 \end{vmatrix} \\ &= \hat{\imath}(4 - 0) - \hat{\jmath}(2t^2-4t^2) + \hat{k}(0-4t) = \langle 4, 2t^2, -4t \rangle \\ |\vec{v}\times\vec{a}|&=\sqrt{16 + 4t^4 + 16t^2} =\sqrt{4(t^2+2)^2} = 2(t^2+2)\\ \end{aligned}\] So the normal acceleration is: \[ a_{N}=\dfrac{|\vec{v}\times\vec{a}|}{|\vec v|} = \dfrac{2(t^2+2)}{t^2+2} = 2 \]
  
  lh,gg
2. at \(t=1\).
  
  At \(t=1\),
  \(a_{T}=2\)
  \(a_{N}=2\)
3. Which component (tangential or normal) of the acceleration is independent of the position on this curve?
  
  The normal acceleration, \(a_{N}=2\) for all \(t\).
Find the tangential and normal acceleration to the curve \(\vec{r} (t)=\langle 2\sin t,3t^2+4,2\cos t\rangle\)
1. for a general value of \(t\).
  
  \(\begin{aligned} a_{T}&=\dfrac{18t}{\sqrt{1+9t^2}} \\ a_{N}&=\dfrac{2\sqrt{9t^2+10}}{\sqrt{1+9t^2}} \end{aligned}\)
  
  To find the tangential acceleration, we use \(a_{T}=\dfrac{d|\vec{v}|}{dt}\): \[\begin{aligned} \vec{v}&=\langle 2\cos t,6t,-2\sin t\rangle \\ |\vec{v}|&=\sqrt{4\cos^2t+36t^2+4\sin^2t} =\sqrt{4+36t^2} \\ &=2\sqrt{1+9t^2} \\ a_{T}&=\dfrac{d|\vec{v}|}{dt}=\dfrac{18t}{\sqrt{1+9t^2}} \end{aligned}\] To find the normal acceleration, we use: \(a_{N}=\kappa|\vec{v}|^2 =\dfrac{|\vec{v}\times\vec{a}|}{|\vec{v}|}\) First, we find \(|\vec{v}\times\vec{a}|\): \[\begin{aligned} \vec a&=\langle -2\sin t,6,-2\cos t \rangle \\ \vec{v}\times\vec{a}&= \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 2\cos t & 6t & -2\sin t \\ -2\sin t & 6 & -2\cos t \end{vmatrix} \\ &=\hat\imath (-12t\cos t+12\sin t) -\hat\jmath (-4\cos^2t-4\sin^2t) \\ &\quad+\hat k(12\cos t+12t\sin t) \\ &=4\langle 3(\sin t-t\cos t),1,3(\cos t+t\sin t)\rangle \\ |\vec{v}\times\vec{a}| &=4\Big[9(\sin^2t-2t\sin t\cos t+t^2\cos^2t)+1 \\ &\quad+9(\cos^2t+2t\sin t\cos t+t^2\sin^2t)\Big]^{1/2} \\ &=4\sqrt{9(1 +t^2)+1} =4\sqrt{9t^2+10} \end{aligned}\] Now we can substitute into the formula for \(a_{N}\): \[\begin{aligned} a_{N}&=\dfrac{4\sqrt{9t^2+10}}{2\sqrt{1+9t^2}} \\ &=\dfrac{2\sqrt{9t^2+10}}{\sqrt{1+9t^2}} \\ \end{aligned}\]
  
  lh
2. at \(t=0\).
  
  At \(t=0\),
  \(a_{T}=0\)
  \(a_{N}=\dfrac{2\sqrt{10}}{\sqrt{1}}=2\sqrt{10}\)

h. Summary & Examples of Curve Computations

Consider the position vector \(\vec{r}(t)=\langle 6\cos t,6\sin t,8t\rangle\).
1. Is this a helix or circle? How can you tell?
  
  This is a helix because the \(z\) component is a linear polynomial.
  
  This is a helix because the \(z\) component is a linear polynomial. If it was a constant, then it would be a circle. The \(x\) and \(y\) components make a circle in the \(xy\)-plane, therefore the helix spirals in the \(z\) direction as shown to the right:
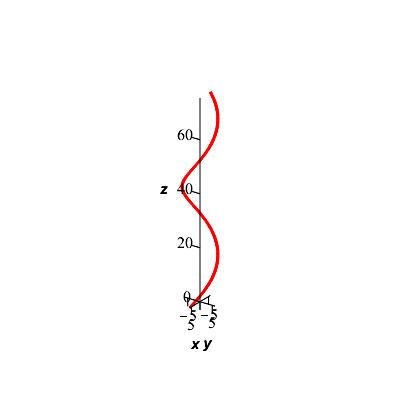
2. Compute the velocity and acceleration of the curve at \(t=\dfrac{\pi}{2}\).
  
  \(\begin{aligned} \vec{v}\left(\dfrac{\pi}{2}\right)&=\langle -6,0,8\rangle \\ \vec{a}\left(\dfrac{\pi}{2}\right)&=\langle 0,-6,0\rangle \\ \end{aligned}\)
  
  The velocity and acceleration are the first and second derivatives of the curve: \[\begin{aligned} \vec{v}(t)&=\langle -6\sin t,6\cos t,8\rangle \\ \vec{a}(t)&=\langle -6\cos t,-6\sin t,0\rangle \\ \end{aligned}\] and evaluate them at \(t=\dfrac{\pi}{2}\): \[\begin{aligned} \vec{v}\left(\dfrac{\pi}{2}\right)&=\langle -6,0,8\rangle \\ \vec{a}\left(\dfrac{\pi}{2}\right)&=\langle 0,-6,0\rangle \\ \end{aligned}\]
  
  gg
Consider the position vector \(\vec{r}(t)=\langle 12\cos t,9,12\sin t\rangle\).
1. Is this a helix or circle? How can you tell?
  
  This is a circle because the \(y\) component is constant.
  
  This is a circle because the \(x\) and \(z\) components are the parameters for a circle while the y component is constant. The \(y\) component is \(9\), meaning this is a circle in a plane parallel to the \(xz\)-plane at \(y=9\) as shown to the right:
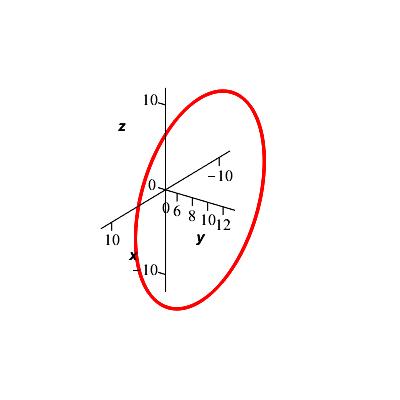
2. Compute the velocity and acceleration of the curve at \(t=2\pi\).
  
  \(\begin{aligned} \vec{v}(2\pi)&=\langle 0,0,12\rangle \\ \vec{a}(2\pi)&=\langle -12,0,0\rangle \end{aligned}\)
  
  The velocity and acceleration are the first and second derivatives of the curve: \[\begin{aligned} \vec{v}(t)&=\langle -12\sin t,0,12\cos t\rangle \\ \vec{a}(t)&=\langle -12\cos t,0,-12\sin t\rangle \\ \end{aligned}\] and evaluate them at \(t=2\pi\): \[\begin{aligned} \vec{v}(2\pi)&=\langle 0,0,12\rangle \\ \vec{a}(2\pi)&=\langle -12,0,0\rangle \end{aligned}\]
  
  gg
Consider the position vector \(\vec{r}(t)=\langle 5t,12\sin t,12\cos t\rangle\).
1. Is this a helix or circle? How can you tell?
  
  This is a helix because the \(x\) component is a linear polynomial.
  
  This is a helix because the \(x\) component is a linear polynomial. If it was a constant, then it would be a circle. The \(y\) and \(z\) components are the parameters for a circle, meaning that in the \(yz\) plane a circle is formed when looking from the \(x\) axis. The helix spirals in the \(x\) direction, as shown to the right:
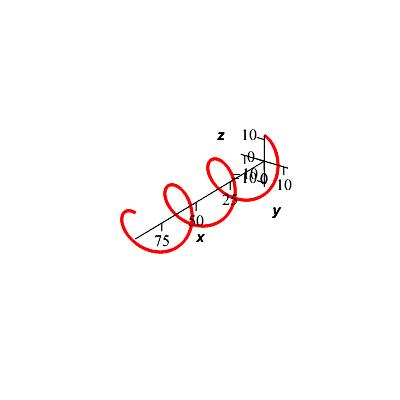
2. What is the length of the curve from \(t=0\) to \(t=\pi\)?
  
  \(\displaystyle L=\int_a^b |\vec{v}|\,dt\)
  
  \(L=13\pi\)
  
  The arclength is the integral of the speed: \[L=\int_{a}^{b} |\vec{v}|\,dt\] First we must find the speed (the magnitude of the velocity vector): \[\begin{aligned} \vec{v}&=\vec{r\,}'(t) =\langle 5,12\cos t,-12\sin t\rangle \\ |\vec{v}| &=\sqrt{5^2+12^2\cos^2t+(-12)^2\sin^2t} \\ &=\sqrt{25+144(\cos^2t+\sin^2t)}=\sqrt{25+144}=13 \\ \end{aligned}\] Finally, we plug this into the arclength formula and compute for the length of the curve: \[L=\int_0^{\pi} 13\,dt=13\pi\]
  
  lh

i. Frenet Frames (Optional)

Verify the Frenet equations for the derivatives of \(\hat{T}\), \(\hat{N}\) and \(\hat{B}\) for the circle: \[ \vec{r}(\theta)=\langle a\cos\theta,a\sin\theta,b\rangle \] where \(a\) and \(b\) are constants.

We must verify: \[\begin{aligned} \dfrac{d\hat{T}}{ds}&=\qquad \quad \kappa \hat{N} \\ \dfrac{d\hat{N}}{ds}&=-\kappa \hat{T} \quad + \quad \tau \hat{B} \\ \dfrac{d\hat{B}}{ds}&=\qquad -\tau \hat{N} \end{aligned}\] Compute \(\hat{T}\), \(\hat{N}\), \(\hat{B}\), \(\kappa\) and \(\tau\). To compute \(\dfrac{d\hat{T}}{ds}\), \(\dfrac{d\hat{T}}{ds}\) and \(\dfrac{d\hat{T}}{ds}\). Remember: \[ \dfrac{d}{ds}=\dfrac{d\theta}{ds}\dfrac{d}{d\theta} =\dfrac{1}{|\vec v|}\dfrac{d}{d\theta} \]

First, we compute \(\hat T\). The velocity and its length are: \[\begin{aligned} \vec{v} &=\langle -a\sin\theta,a\cos\theta,0\rangle \\ |\vec{v}| &=\sqrt{a^2\sin^2\theta+a^2\cos^2\theta}=a \end{aligned}\] So the unit tangent vector is: \[ \hat{T}=\dfrac{\vec{v}}{|\vec{v}|} =\langle -\sin\theta,\cos\theta,0\rangle \] Second, we compute \(\hat B\). The acceleration, the cross product, \(\vec v\times\vec a\), and its length are: \[\begin{aligned} \vec{a} &=\langle -a\cos\theta,-a\sin\theta,0\rangle \\ \vec{v}\times\vec{a} &=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ -a\sin\theta & a\cos\theta & 0 \\ -a\cos\theta & -a\sin\theta & 0 \end{vmatrix} \\ &=\hat{\imath}(0) -\hat{\jmath}(0) +\hat{k}(a^2\sin^2\theta+a^2\cos^2\theta) \\ &=\langle 0,0,a^2\rangle \\ |\vec{v}\times\vec{a}| &=a^2 \\ \end{aligned}\] So the unit binormal vector is: \[ \hat{B} =\dfrac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|} =\langle 0,0,1\rangle \] Third, we compute \(\hat N\): \[\begin{aligned} \hat N&=\hat B\times\hat T =\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ 0 & 0 & 1 \\ -\sin\theta & \cos\theta & 0 \\ \end{vmatrix} \\ &=\hat{\imath}(-\cos\theta) -\hat{\jmath}(\sin\theta) +\hat{k}(0) \\ &=\langle -\cos\theta,-\sin\theta,0\rangle \\ \end{aligned}\] To determine the curvature and torsion, we compute the jerk and triple product: \[\begin{aligned} \vec j =\langle a\sin\theta,-a\cos\theta,0\rangle \\ \vec v\times\vec a\cdot\vec j =0 \end{aligned}\] So the curvature and torsion are: \[\begin{aligned} \kappa&=\dfrac{|\vec{v}\times\vec{a}|}{|\vec{v}|^3} =\dfrac{a^2}{a^3} =\dfrac{1}{a} \\ \tau&=\dfrac{\vec{v}\times\vec{a}\cdot\vec{j}}{|\vec{v}\times\vec{a}|^2} =0 \end{aligned}\] Finally, we must verify the Frenet equations: \[\begin{aligned} \dfrac{d\hat{T}}{ds}&=\qquad \quad \kappa \hat{N} \\ \dfrac{d\hat{N}}{ds}&=-\kappa \hat{T} \quad + \quad \tau \hat{B} \\ \dfrac{d\hat{B}}{ds}&=\qquad -\tau \hat{N} \end{aligned}\] We compute each side. First for \(\hat{T}\): \[\begin{aligned} \dfrac{d\hat{T}}{ds}&=\dfrac{1}{|\vec{v}|}\dfrac{d\hat{T}}{d\theta} =\dfrac{1}{a}\langle -\cos\theta,-\sin\theta,0\rangle \\ \kappa\hat N &=\dfrac{1}{a}\langle -\cos\theta,-\sin\theta,0\rangle \end{aligned}\] which agree. Second for \(\hat{N}\): \[\begin{aligned} \dfrac{d\hat{N}}{ds}&=\dfrac{1}{|\vec{v}|}\dfrac{d\hat{N}}{d\theta} =\dfrac{1}{a}\langle \sin\theta,-\cos\theta,0\rangle \\ -\kappa\hat T+\tau\hat B &=\dfrac{-1}{a}\langle -\sin\theta,\cos\theta,0\rangle +0\langle 0,0,1\rangle \\ &=\dfrac{1}{a}\langle \sin\theta,-\cos\theta,0\rangle \end{aligned}\] which also agree. And finally for \(\hat{B}\): \[\begin{aligned} \dfrac{d\hat{B}}{ds}&=\dfrac{1}{|\vec{v}|}\dfrac{d\hat{B}}{d\theta} =\dfrac{1}{a}\langle 0,0,0\rangle=\langle 0,0,0\rangle \\ -\tau\hat{N} &=0\langle -\cos\theta,-\sin\theta,0\rangle=\langle 0,0,0\rangle \end{aligned}\] which also agree.

lh
Verify the Frenet equations for the derivatives of \(\hat{T}\), \(\hat{N}\) and \(\hat{B}\) for a general helix: \[ \vec{r}(\theta)=\langle a\cos\theta,a\sin\theta,b\,\theta\rangle \] where \(a\) and \(b\) are constants.

First, we compute \(\hat T\). The velocity and its length are: \[\begin{aligned} \vec{v} &=\langle -a\sin\theta,a\cos\theta,b\rangle \\ |\vec{v}| &=\sqrt{a^2\sin^2\theta+a^2\cos^2\theta+b^2} =\sqrt{a^2+b^2} \end{aligned}\] So the unit tangent vector is: \[ \hat{T}=\dfrac{\vec{v}}{|\vec{v}|} =\dfrac{1}{\sqrt{a^2+b^2}} \langle -a\sin\theta,a\cos\theta,b\rangle \] Second, we compute \(\hat B\). The acceleration, the cross product, \(\vec v\times\vec a\), and its length are: \[\begin{aligned} \vec{a} &=\langle -a\cos\theta,-a\sin\theta,0\rangle \\ \vec{v}\times\vec{a} &=\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ -a\sin\theta & a\cos\theta & b \\ -a\cos\theta & -a\sin\theta & 0 \end{vmatrix} \\ &=\hat{\imath}(ab\sin\theta) -\hat{\jmath}(ab\cos\theta) +\hat{k}(a^2\sin^2\theta+a^2\cos^2\theta) \\ &=\langle ab\sin\theta,-ab\cos\theta,a^2\rangle \\ |\vec{v}\times\vec{a}| &=\sqrt{a^2b^2\sin^2\theta+a^2b^2\cos^2\theta+a^4} \\ &=a\sqrt{a^2+b^2} \\ \end{aligned}\] So the unit binormal vector is: \[\begin{aligned} \hat{B} &=\dfrac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|} =\dfrac{1}{a\sqrt{a^2+b^2}}\langle ab\sin\theta,-ab\cos\theta,a^2\rangle \\ &=\dfrac{1}{\sqrt{a^2+b^2}}\langle b\sin\theta,-b\cos\theta,a\rangle \\ \end{aligned}\] Third, we compute \(\hat N\). \[\begin{aligned} \hat N&=\hat B\times\hat T =\dfrac{1}{\sqrt{a^2+b^2}^{\,2}}\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ b\sin\theta & -b\cos\theta & a \\ -a\sin\theta & a\cos\theta & b \\ \end{vmatrix} \\ &=\dfrac{1}{a^2+b^2}\Big[\hat{\imath}(-b^2\cos\theta-a^2\cos\theta) \\ &\qquad\qquad\quad-\hat{\jmath}(b^2\sin\theta+a^2\sin\theta) \\ &\qquad\qquad\qquad+\hat{k}(ab\sin\theta\cos\theta-ab\sin\theta\cos\theta)\Big] \\ &=\langle -\cos\theta,-\sin\theta,0\rangle \\ \end{aligned}\] To determine the curvature and torsion, we compute the jerk and triple product: \[\begin{aligned} \vec j &=\langle a\sin\theta,-a\cos\theta,0\rangle \\ \vec v\times\vec a\cdot\vec j &=a^2b\sin^2\theta+a^2b\cos^2\theta=a^2b \end{aligned}\] So the curvature and torsion are: \[\begin{aligned} \kappa&=\dfrac{|\vec{v}\times\vec{a}|}{|\vec{v}|^3} =\dfrac{a\sqrt{a^2+b^2}}{(a^2+b^2)^{3/2}} =\dfrac{a}{a^2+b^2} \\ \tau&=\dfrac{\vec{v}\times\vec{a}\cdot\vec{j}}{|\vec{v}\times\vec{a}|^2} =\dfrac{a^2b}{\left(a\sqrt{a^2+b^2}\right)^2} =\dfrac{b}{a^2+b^2} \end{aligned}\] Finally, we must verify the Frenet equations: \[\begin{aligned} \dfrac{d\hat{T}}{ds}&=\qquad \quad \kappa \hat{N} \\ \dfrac{d\hat{N}}{ds}&=-\kappa \hat{T} \quad + \quad \tau \hat{B} \\ \dfrac{d\hat{B}}{ds}&=\qquad -\tau \hat{N} \end{aligned}\] We compute each side. First for \(\hat{T}\): \[\begin{aligned} \dfrac{d\hat{T}}{ds}&=\dfrac{1}{|\vec{v}|}\dfrac{d\hat{T}}{d\theta} =\dfrac{1}{a^2+b^2}\langle -a\cos\theta,-a\sin\theta,0\rangle \\ \kappa\hat N &=\dfrac{a}{a^2+b^2}\langle -\cos\theta,-\sin\theta,0\rangle \end{aligned}\] which agree. Second for \(\hat{N}\): \[\begin{aligned} \dfrac{d\hat{N}}{ds}&=\dfrac{1}{|\vec{v}|}\dfrac{d\hat{N}}{d\theta} =\dfrac{1}{\sqrt{a^2+b^2}}\langle \sin\theta,-\cos\theta,0\rangle \\ -\kappa\hat T+\tau\hat B &=\dfrac{-a}{(a^2+b^2)^{3/2}}\langle -a\sin\theta,a\cos\theta,b\rangle \\ &\quad+\dfrac{b}{(a^2+b^2)^{3/2}}\langle b\sin\theta,-b\cos\theta,a\rangle \\ &=\dfrac{1}{\sqrt{a^2+b^2}}\langle \sin\theta,-\cos\theta,0\rangle \end{aligned}\] which also agree. And finally for \(\hat{B}\): \[\begin{aligned} \dfrac{d\hat{B}}{ds}&=\dfrac{1}{|\vec{v}|}\dfrac{d\hat{B}}{d\theta} =\dfrac{1}{a^2+b^2}\langle b\cos\theta,b\sin\theta,0\rangle \\ -\tau\hat{N} &=\dfrac{-b}{a^2+b^2}\langle -\cos\theta,-\sin\theta,0\rangle \end{aligned}\] which also agree.

lh
Verify the Frenet equations for the derivatives of \(\hat{T}\), \(\hat{N}\) and \(\hat{B}\) for the twisted cubic \(\vec{r}(t)=\left\langle 2t,t^2,\dfrac{1}{3}t^3\right\rangle\).

For the curve: \[\vec{r}(t)=\left\langle 2t,t^2,\dfrac{1}{3}t^3\right\rangle\] We first find the unit tangent vector, \(\hat{T}=\dfrac{\vec{v}}{|\vec{v}|}\): \[\begin{aligned} \vec{v}&=\langle 2,2t,t^2\rangle \\ |\vec{v}|&=\sqrt{4+4t^2+t^4} = 2+t^2\\ \hat{T}&=\dfrac{\vec{v}}{|\vec{v}|} =\dfrac{1}{2+t^2}\langle 2,2t,t^2\rangle\\ \end{aligned}\] We next find the unit binormal vector, \(\hat{B}=\dfrac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}\): \[\begin{aligned} \vec{a} &= \langle 0,2,2t \rangle \\ \vec{v}\times\vec{a}&= \begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ 2 & 2t & t^2 \\ 0 & 2 & 2t \end{vmatrix} =\hat{\imath}(4t^2-2t^2)-\hat{\jmath}(4t)+\hat{k}(4) \\ &=2\langle t^2,-2t,2 \rangle \\ |\vec{v}\times\vec{a}| &=2\sqrt{t^4+4t^2+4} = 2(2+t^2)\\ \hat{B}&=\dfrac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|} =\dfrac{1}{2+t^2}\langle t^2,-2t, 2 \rangle \end{aligned}\] Finally, we find the unit normal vector, \(\hat{N}\): \[\begin{aligned} \hat N&=\hat B\times\hat T =\dfrac{1}{(2+t^2)^2}\begin{vmatrix} \hat{\imath} & \hat{\jmath} & \hat{k} \\ t^2 & -2t & 2 \\ 2 & 2t & t^2 \end{vmatrix} \\ &=\dfrac{\hat{\imath}(-2t^3-4t)-\hat{\jmath}(t^4-4)+\hat{k}(2t^3+4t)}{(2+t^2)^2} \\ &=\dfrac{\langle-2t(2+t^2),(2+t^2)(2-t^2),2t(2+t^2)\rangle}{(2+t^2)^2} \\ &=\dfrac{1}{2+t^2}\langle -2t, 2-t^2, 2t\rangle \end{aligned}\] Based on previous values and \(\vec\jmath=\langle0,0,2\rangle\), we find the curvature and torsion: \[\begin{aligned} \kappa&=\dfrac{|\vec{v}\times\vec{a}|}{|\vec{v}|^3} =\dfrac{2(2+t^2)}{(2+t^2)^3} =\dfrac{2}{(2+t^2)^2} \\ \tau&=\dfrac{\vec{v}\times\vec{a}\cdot\vec\jmath} {|\vec{v}\times\vec{a}|^2} =\dfrac{2\langle t^2,-2t,2 \rangle \cdot \langle 0,0,2 \rangle}{4(2+t^2)^2} =\dfrac{2}{(2+t^2)^2} \end{aligned}\] Finally, we must verify the Frenet equations: \[\begin{aligned} \dfrac{d\hat{T}}{ds}&=\qquad \quad \kappa \hat{N} \\ \dfrac{d\hat{N}}{ds}&=-\kappa \hat{T} \quad + \quad \tau \hat{B} \\ \dfrac{d\hat{B}}{ds}&=\qquad -\tau \hat{N} \end{aligned}\] We compute each side. First for \(\hat{T}\): \[\begin{aligned} \dfrac{d\hat{T}}{ds}&=\dfrac{1}{|\vec{v}|}\dfrac{d\hat{T}}{dt}\\ &=\dfrac{1}{2+t^2}\dfrac{d}{dt} \left\langle \dfrac{2}{2+t^2},\dfrac{2t}{2+t^2},\dfrac{t^2}{2+t^2}\right\rangle \\ &=\dfrac{1}{2+t^2} \left\langle \dfrac{-4t}{(2+t^2)^2},\dfrac{2(2+t^2)-2t2t}{(2+t^2)^2},\right. \\ &\qquad\qquad\qquad\left.\dfrac{(2+t^2)2t-t^22t}{(2+t^2)^2}\right\rangle \\ &=\dfrac{1}{(2+t^2)^3}\langle -4t,4-2t^2,4t\rangle \\ \kappa\hat N &=\dfrac{2}{(2+t^2)^3}\langle -2t, 2-t^{2}, 2t\rangle \end{aligned}\] which agree. Second for \(\hat{N}\): \[\begin{aligned} \dfrac{d\hat{N}}{ds}&=\dfrac{1}{|\vec{v}|}\dfrac{d\hat{N}}{dt}\\ &=\dfrac{1}{2+t^2}\dfrac{d}{dt} \left\langle \dfrac{-2t}{2+t^2},\dfrac{2-t^2}{2+t^2},\dfrac{2t}{2+t^2}\right\rangle \\ &=\dfrac{1}{2+t^2} \left\langle \dfrac{-2(2+t^2)+2t2t}{(2+t^2)^2},\dfrac{-2t(2+t^2)-(2-t^2)(2t)}{(2+t^2)^2},\right. \\ &\qquad\qquad\qquad\left.\dfrac{2(2+t^2)-2t2t}{(2+t^2)^2}\right\rangle \\ &=\dfrac{1}{(2+t^2)^3}\left\langle -4+2t^2, -8t, 4-2t^2\right\rangle\\ -\kappa\hat T+\tau\hat B &=\dfrac{-2}{(2+t^2)^3}\langle 2,2t,t^2\rangle +\dfrac{2}{(2+t^2)^3}\langle t^2,-2t, 2 \rangle \\ &=\dfrac{1}{(2+t^2)^3}\langle -4+2t^2,-8t,-2t^2+4\rangle\\ \end{aligned}\] which also agree. And finally for \(\hat{B}\): \[\begin{aligned} \dfrac{d\hat{B}}{ds}&=\dfrac{1}{|\vec{v}|}\dfrac{d\hat{B}}{dt}\\ &=\dfrac{1}{2+t^2}\dfrac{d}{dt} \left\langle \dfrac{t^2}{2+t^2},\dfrac{-2t}{2+t^2},\dfrac{2}{2+t^2}\right\rangle \\ &=\dfrac{1}{2+t^2} \left\langle \dfrac{2t(2+t^2)-2t^3}{(2+t^2)^2},\dfrac{-2(2+t^2)+2t2t}{(2+t^2)^2},\right. \\ &\qquad\qquad\qquad\left.\dfrac{-4t}{(2+t^2)^2}\right\rangle \\ &=\dfrac{1}{(2+t^2)^3}\langle 4t,-4+2t^2,-4t\rangle\\ -\tau\hat{N} &=\dfrac{-2}{(2+t^2)^3}\langle -2t, 2-t^{2}, 2t\rangle \\ &=\dfrac{1}{(2+t^2)^3}\langle 4t, -4+2t^{2}, -4t\rangle \end{aligned}\] which also agree.

lh,gg

. Tutorial on Properties of Curves

Review Exercises

Find the velocity, acceleration and jerk of the curve \(\vec r(t)=\langle \ln t,t^2+1,\tan t\rangle\) at the point when \(t=\pi\).

\(\begin{aligned} \vec v(\pi)&=\left\langle \dfrac{1}{\pi},2\pi,1\right\rangle \\ \vec a(\pi)&=\left\langle -\,\dfrac{1}{\pi^2},2,0\right\rangle \\ \vec \jmath(\pi)&=\left\langle \dfrac{2}{\pi^3},0,2\right\rangle \end{aligned}\)

The velocity is the derivative of \(\vec r(t)\) term by term: \[\begin{aligned} \vec v(t)&=\vec r'(t)=\dfrac{d\vec r}{dt} =\left\langle \dfrac{dr_1}{dt},\dfrac{dr_2}{dt},\dfrac{dr_3}{dt}\right\rangle \\ &=\left\langle \dfrac{1}{t},2t,\sec^2 t\right\rangle \end{aligned}\] The acceleration is the derivative of \(\vec v(t)\): \[\begin{aligned} \vec a(t)&=\vec v'(t) \\ &=\left\langle -\,\dfrac{1}{t^2},2,2\sec^2 t\tan t\right\rangle \end{aligned}\] The jerk is the derivative of \(\vec a(t)\): \[\begin{aligned} \vec \jmath(t)&=\vec a'(t) \\ &=\left\langle \dfrac{2}{t^3},0,4\sec^2 t\tan^2 t+2\sec^4 t\right\rangle \end{aligned}\] Next, plug in \(t = \pi\): \[\begin{aligned} \vec v(\pi)&=\left\langle \dfrac{1}{\pi},2\pi,1\right\rangle \\ \vec a(\pi)&=\left\langle -\,\dfrac{1}{\pi^2},2,0\right\rangle \\ \vec \jmath(\pi)&=\left\langle \dfrac{2}{\pi^3},0,2\right\rangle \end{aligned}\]

gg
Consider the position vector \(\vec{r}(t)=\langle21\cos t,21\sin t,20t\rangle\). Find:
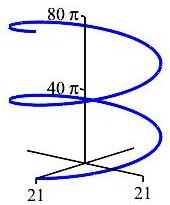
1. the velocity vector and speed.
  
  \(\vec{v}(t)=\left\langle -21\sin t,21\cos t,20 \right\rangle\)
  \(\text{speed}=|\vec{v}|=29\)
  
  Velocity is the derivative of position with respect to time. So: \[ \vec v(t) =\dfrac{d\vec{r}}{dt} =\left\langle -21\sin t,21\cos t,20 \right\rangle \] The speed is its length: \[\begin{aligned} \text{speed} &= |\vec{v}| = \sqrt{(-21\sin t)^{2}+(21\cos t)^{2}+20^{2}} \\ &= \sqrt{21^{2}(\sin^2 t+\cos^2 t)+20^{2}}= 29 \end{aligned}\]
  
  gg
2. the acceleration vector.
  
  \(\vec{a}(t)=\langle -21\cos t,-21\sin t,0 \rangle\)
  
  Acceleration is the derivative of velocity with respect to time. So: \[ \vec{a}(t)=\dfrac{d\vec{v}}{dt} =\langle -21\cos t,-21\sin t,0 \rangle \]
  
  gg
3. the jerk vector.
  
  \(\vec{\jmath}(t)=\langle 21\sin t,-21\cos t,0 \rangle\)
  
  Jerk is the derivative of acceleration with respect to time. So: \[ \vec{\jmath}(t)=\dfrac{d\vec{a}}{dt} =\left\langle 21\sin t,-21\cos t,0 \right\rangle \]
  
  gg
4. the arc length from an arbitrary \(a\) to an arbitrary \(b\).
  
  \(L=29(b-a)\)
  
  The arclength between \(t=a\) and \(t=b\) is: \[ L=\int_A^B\,ds =\int_a^b |\vec{v}|\,dt = \int_a^b 29\,dt = 29(b-a) \]
  
  gg
5. the arclength parameter \(s=s(t)\) starting from \(t=0\).
  
  \(s=29t\)
  
  The arclength parameter starting from \(t=0\) is: \[ s(t) = \int_0^t |\vec{v}|\,dt = \int_0^t 29\,dt = 29t \]
  
  gg
6. the unit tangent vector.
  
  \(\hat{T}=\left\langle -\,\dfrac{21}{29}\sin t,\dfrac{21}{29}\cos t,\dfrac{20}{29} \right\rangle\)
  
  The unit tangent vector is: \[\begin{aligned} \hat{T}&=\dfrac{\vec{v}}{|\vec{v}|} =\dfrac{\left\langle -21\sin t,21\cos t,20 \right\rangle}{29} \\ &=\left\langle -\,\dfrac{21}{29}\sin t,\dfrac{21}{29}\cos t,\dfrac{20}{29} \right\rangle \end{aligned}\]
  
  gg
7. the unit binormal vector.
  
  \(\hat{B}=\left\langle \dfrac{20}{29}\sin t,-\,\dfrac{20}{29}\cos t,\dfrac{21}{29} \right\rangle\)
  
  The unit binormal vector is \(\hat{B}=\dfrac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}\). So first we compute \(\vec{v}\times\vec{a}\) and its magnitude: \[\begin{aligned} \vec{v}\times\vec{a}&= \begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ -21\sin t & 21\cos t & 20 \\ -21\cos t & -21\sin t & 0 \end{vmatrix} \\ &= \hat\imath (20(21)\sin t)- \hat\jmath (20(21)\cos t) +\hat k (21^2(\sin^2 t + \cos^2 t)) \\ &= 21\left\langle 20\sin t,-20\cos t,21\right\rangle \\ |\vec{v}\times\vec{a}| &= 21\sqrt{(20\sin t)^{2} + (-20\cos t)^{2} +21^{2}} \\ &= 21\sqrt{20^{2} +21^{2}} = 21(29) \end{aligned}\] Now we substitute and find \(\hat{B}\): \[\begin{aligned} \hat{B}&=\dfrac{21\left\langle 20\sin t,-20\cos t,21\right\rangle}{21(29)}\\ &= \left\langle \dfrac{20}{29}\sin t,-\,\dfrac{20}{29}\cos t,\dfrac{21}{29} \right\rangle \end{aligned}\]
  
  gg
8. the unit normal vector.
  
  \(\hat{N}=\left\langle -\cos t,-\sin t,0 \right\rangle\)
  
  The unit normal vector is \(\hat{N}=\hat{B}\times\hat{T}\). So: \[\begin{aligned} \hat{N} &= \hat{B}\times\hat{T} \\ &= \dfrac{\langle 20\sin t,-20\cos t,21\rangle}{29} \times \dfrac{\langle -21\sin t,21\cos t,20 \rangle}{29} \\ &= \dfrac{1}{29^2}\begin{vmatrix} \hat\imath & \hat\jmath & \hat k \\ 20\sin t & -20\cos t & 21\\ -21\sin t & 21\cos t & 20 \end{vmatrix}\\ &= \dfrac{1}{29^2}\big[\hat\imath (-20^2\cos t-21^2\cos t)\\ &\qquad\quad-\hat\jmath (20^2 \sin t+21^2 \sin t) \\ &\qquad\quad+\hat k (20(21)\sin t \cos t-20(21)\sin t \cos t ) \big]\\ &= \dfrac{1}{29^2}\langle -29^2\cos t,-29^2\sin t, 0\rangle \\ &= \langle -\cos t,-\sin t, 0\rangle \end{aligned}\]
  
  gg
9. the curvature of the curve.
  
  \(\kappa=\dfrac{21}{29^2}\)
  
  We previously found: \[ |\vec v|=29 \qquad \text{and} \qquad |\vec{v}\times\vec{a}|=21(29) \] So the curvature is: \[ \kappa = \dfrac{|\vec{v}\times\vec{a}|}{|\vec{v}|^3} =\dfrac{21(29)}{29^3} =\dfrac{21}{29^2} \]
  
  gg
10. the torsion of the curve.
  
  \(\tau=\dfrac{20}{29^2}\)
  
  We previously found: \[\begin{aligned} \vec{v}\times\vec{a}&=21\langle20\sin t, -20\cos t, 21\rangle \\ |\vec{v}\times\vec{a}|&=21(29) \\ \vec\jmath&=\langle21\sin t, -21\cos t, 0\rangle \end{aligned}\] So the torsion is: \[ \tau=\dfrac{\vec{v}\times\vec{a}\cdot\vec{j}}{|\vec{v}\times\vec{a}|^2} =\dfrac{21[21(20)\sin^2t+21(20)\cos^2t]}{21^2 29^2} =\dfrac{20}{29^2} \]
  
  gg
11. the tangential acceleration.
  Compute it two ways.
  
  \(a_{T}=0\)
  
  The tangential acceleration is: \[\begin{aligned} a_{T}&=\vec{a}\cdot\hat{T} \\ &=\langle -21\cos t,-21\sin t,0 \rangle \cdot \langle -\,\dfrac{21}{29}\sin t,\dfrac{21}{29}\cos t,\dfrac{20}{29} \rangle \\ &=\dfrac{21^2}{29}\sin t\cos t-\,\dfrac{21^2}{29}\sin t\cos t =0 \\ \end{aligned}\] or: \[ a_{T}=\dfrac{d}{dt}|\vec{v}|=\dfrac{d}{dt}29=0 \]
  
  lh,gg
12. the normal acceleration.
  Compute it two ways.
  
  \(a_{N}=21\)
  
  The normal acceleration is: \[\begin{aligned} a_{N}&=\vec{a}\cdot\hat{N} \\ &=\langle -21\cos t,-21\sin t,0\rangle\cdot\langle -\cos t,-\sin t,0\rangle \\ &=21\cos^2t+21\sin^2t =21 \end{aligned}\] or: \[ a_{N}=\kappa|\vec{v}|^2=\dfrac{21}{29^2}\cdot29^2=21 \]
  
  lh,gg

PY: All Checked

3. Properties of Curves

Exercises

Review Exercises

Heading