8. Properties of Curves
b. Limits and Derivatives of Vector Functions
2. Derivatives of Vector Functions
The definition of the derivative of a vector function mimics that for an ordinary function:
The derivative of a vector function \(\vec{f}(t)=\left\langle f_1(t),f_2(t),f_3(t)\right\rangle\) is: \[ \dfrac{d\vec{f}}{dt}=\lim_{h\rightarrow 0}\dfrac{\vec{f}(t+h)-\vec{f}(t)}{h} \] provided the limit exists.
Although this definition is useful and essential for theoretical purposes, the following proposition give a formula which is much better for computational purposes.
The derivative of a vector function
\(\vec{f}(t)=\left\langle f_1(t),f_2(t),f_3(t)\right\rangle\) is:
\[
\dfrac{d\vec{f}}{dt}
=\left\langle \dfrac{df_1}{dt},\dfrac{df_2}{dt},\dfrac{df_3}{dt}\right\rangle
\]
provided the derivatives exists.
We use addition and scalar multiplication of vectors and the definition of a limit of a vector function: \[\begin{aligned} \dfrac{d\vec{f}}{dt} &=\lim_{h\rightarrow 0}\dfrac{\vec{f}(t+h)-\vec{f}(t)}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{\left\langle f_1(t+h),f_2(t+h),f_3(t+h)\right\rangle -\left\langle f_1(t),f_2(t),f_3(t)\right\rangle}{h} \\ &=\lim_{h\rightarrow 0}\dfrac{\left\langle f_1(t+h)-f_1(t), f_2(t+h)-f_2(t),f_3(t+h)-f_3(t)\right\rangle}{h} \\ &=\lim_{h\rightarrow 0}\left\langle \dfrac{f_1(t+h)-f_1(t)}{h},\dfrac{f_2(t+h)-f_2(t)}{h}, \dfrac{f_3(t+h)-f_3(t)}{h}\right\rangle \\ &=\left\langle \lim_{h\rightarrow 0}\dfrac{f_1(t+h)-f_1(t)}{h}, \lim_{h\rightarrow 0}\dfrac{f_2(t+h)-f_2(t)}{h}, \lim_{h\rightarrow 0}\dfrac{f_3(t+h)-f_3(t)}{h}\right\rangle \\ &=\left\langle \dfrac{df_1}{dt},\dfrac{df_2}{dt},\dfrac{df_3}{dt}\right\rangle \end{aligned}\]
In other words, to take the derivative of a vector function we simply take the derivative of each component.
We can now define the velocity:
Given a parametric curve \(\vec{r}(t)=\left\langle x(t),y(t),z(t)\right\rangle\), its velocity is its derivative: \[ \vec{v}(t)=\dfrac{d\vec{r}}{dt} =\left\langle \dfrac{dx}{dt},\dfrac{dy}{dt},\dfrac{dz}{dt}\right\rangle \]
Find the velocity of the unit circle \(\vec{r}(t)=(\cos t,\sin t)\). Plot the circle and several velocity vectors for \(0 \le t \le \dfrac{3\pi}{2}\).
\(
\vec{v}(t)=\dfrac{d\vec{r}}{dt}=\langle -\sin t,\cos t\rangle
\)
\[\begin{aligned}
&\vec{r}(0)=(1,0)
&&\vec{v}(0)=\langle 0,1\rangle \\
&\vec{r}\left(\dfrac{\pi}{4}\right)
=\left(\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\right)
&&\vec{v}\left(\dfrac{\pi}{4}\right)
=\left\langle \dfrac{-1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\right\rangle \\
&\vec{r}\left(\dfrac{\pi}{2}\right)=(0,1)
&&\vec{v}\left(\dfrac{\pi}{2}\right)=\langle -1,0\rangle \\
&\vec{r}\left(\dfrac{3\pi}{4}\right)
=\left(\dfrac{-1}{\sqrt{2}},\dfrac{1}{\sqrt{2}}\right)\qquad
&&\vec{v}\left(\dfrac{3\pi}{4}\right)
=\left\langle \dfrac{-1}{\sqrt{2}},\dfrac{-1}{\sqrt{2}}\right\rangle \\
&\vec{r}(\pi)=(-1,0)
&&\vec{v}(\pi)=\langle 0,-1\rangle \\
&\vec{r}\left(\dfrac{5\pi}{4}\right)
=\left(\dfrac{-1}{\sqrt{2}},\dfrac{-1}{\sqrt{2}}\right)
&&\vec{v}\left(\dfrac{5\pi}{4}\right)
=\left\langle \dfrac{1}{\sqrt{2}}, \dfrac{-1}{\sqrt{2}}\right\rangle \\
&\vec{r}\left(\dfrac{3\pi}{2}\right)=(0,-1)
&&\vec{v}\left(\dfrac{3\pi}{2}\right)
=\left\langle 1,0\right\rangle \\
\end{aligned}\]

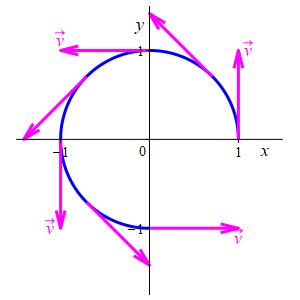
In the above graph, notice that the velocity vectors are always tangent to the curve. This is no accident.
The velocity of a parametric curve is always tangent to the curve.
The proof depends heavily on the limit definition of the derivative. It is important to read the proof:
The velocity, \(\vec{v}\), is the derivative of the position
vector, \(\vec{r}\). We write the derivative as a limit:
\[
\vec{v}=\lim_{h\rightarrow 0}\dfrac{\vec{r}(t+h)-\vec{r}(t)}{h}
\]
The numerator is the
secant vector
from \(\vec{r}(t)\) to \(\vec{r}(t+h)\). (Shown in orange)
As \(h\) gets smaller, the direction of the secant vector approaches the
direction of the tangent vector, but (unfortunately) its length goes to
zero. Dividing by \(h\) gives the
secant quotient vector
from \(\vec{r}(t)\) to \(\vec{r}(t+h)\). (Shown in green)
Its direction is the same as that of the secant vector but its length
may not go to zero. (Their lengths are equal when \(h=1\).)
If the limit exists, then the direction of
\(\vec{v}\) is the direction of the tangent vector.

The animation shows a parabola (in blue) along with
its tangent line at \(\vec{r}(2)\) (in magenta)
its secant vectors at \(\vec{r}(2)\) (in orange)
its secant quotient vectors at \(\vec{r}(2)\) (in green).
As \(h\) gets smaller, the directions of the secant vectors and the secant
quotient vectors approach the direction of the tangent line. The lengths of the
secant vectors approach \(0\) but the lengths of the secant quotient vectors
do not. For \(h \gt 1\), the secant quotient is shorter than the secant, but
for \(h \lt 1\), the secant quotient is longer.
As a consequence of the proposition, we have:
For a parametric curve, the tangent vector is the velocity vector; they are synonyms.
Find the tangent vector to the curve \(\vec{r}(t)=\left(t,\dfrac{2}{t},t^{3}\right)\).
\(\vec{v}(t)=\left\langle 1,\dfrac{-2}{t^2},3t^2\right\rangle\)
Just differentiate: \[ \vec{v}(t) =\dfrac{d\vec r}{dt} =\left\langle 1,\dfrac{-2}{t^2},3t^2\right\rangle \]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum