13. Volume
a1a. Volume by Slicing - Example 1
Find the volume of the solid whose base is the triangle with vertices \((0,0)\), \((4,0)\) and \((0,2)\) and whose cross-sections perpendicular to the \(y\)-axis are semicircles with a diameter on the base.
Here are the base with one cross-section and an accumulation of cross sections to form the final solid:
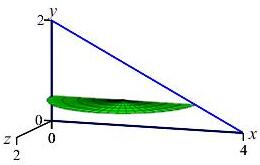
one Cross Section
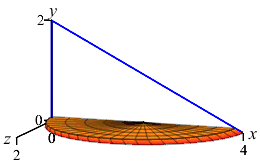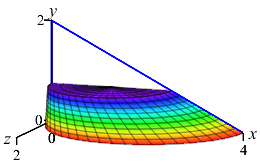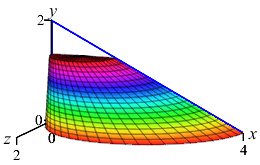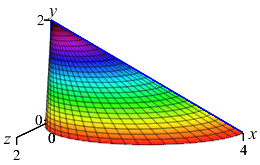
and the Solid
Typically, it is difficult to draw the solid shape. Luckily, a diagram of the base and one slice (as given above on the left) is usually sufficient. However, for your edification, here is an animation (above on the right) of the slices being accumulated to form the complete solid. Each horizontal slice is a semicircle whose diameter \(d\) is the width of the base triangle at height \(y\). So its area is: \[ A=\dfrac{1}{2}\pi r^2=\dfrac{1}{2}\pi\left(\dfrac{d}{2}\right)^2 \] To find \(d\), we use similar triangles. In the Base figure above, the small triangle has legs \(2-y\) and \(x=d\) while the big triangle has legs \(2\) and \(4\). So: \[ \dfrac{d}{2-y}=\dfrac{4}{2} \] \[ A=\dfrac{1}{2}\pi\left(\dfrac{2(2-y)}{2}\right)^2 =\dfrac{1}{2}\pi(2-y)^2 \] The volume is then the integral of the cross-sectional area: \[\begin{aligned} V&=\int_0^2 \dfrac{1}{2}\pi(2-y)^2\,dy =\dfrac{\pi}{2}\left[\dfrac{(2-y)^3}{-3}\right]_0^2 \\ &=\dfrac{\pi}{2}\left(0+\dfrac{2^3}{3}\right) =\dfrac{4}{3}\pi \end{aligned}\]
In this problem, the answer is easy to check using high school geometry, The solid is half of a cone of radius \(r=2\) and height \(h=2\). So the volume is: \[ V=\dfrac{1}{2}\left(\dfrac{1}{3}\pi r^2 h\right) =\dfrac{1}{2}\left(\dfrac{1}{3}\pi 2^2 2\right)=\dfrac{4}{3}\pi \]