13. Volume
Recall: The Volume of a Solid computed using Thin Disks is \[ V=\int_a^b \pi f(x)^2\,dx \qquad \text{or} \qquad V=\int_a^b \pi f(y)^2\,dy \]
c1b. Volume using Thin Disks - Example 2
Now we come to volumes of revolution which do not have a classical formula:
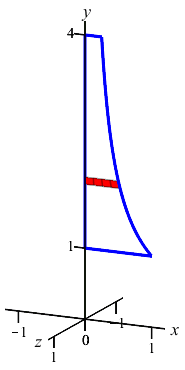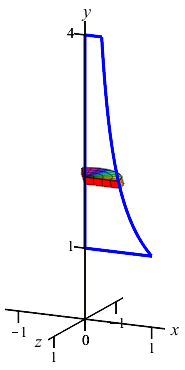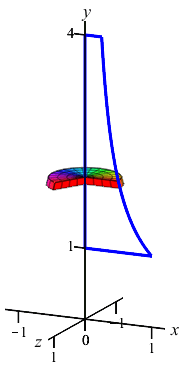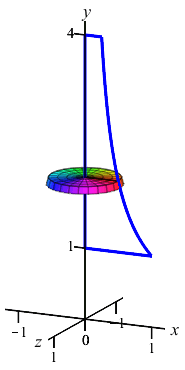
The region between the curve \(x=\dfrac{1}{y}\) and the \(y\)-axis for \(1 \le y \le 4\) is rotated about the \(y\)-axis. Find the volume swept out.
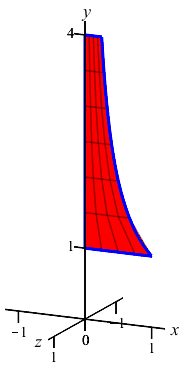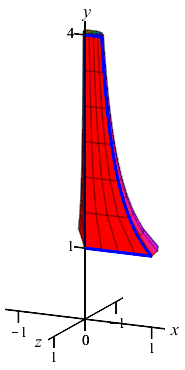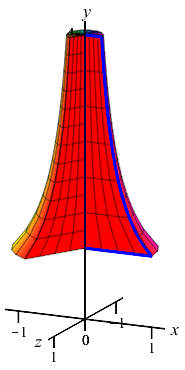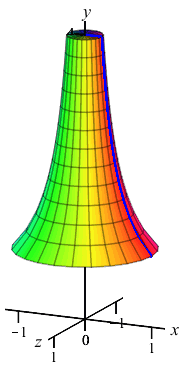
The curve is a function of \(y\); so this is a \(y\)-integral and we cut up the \(y\)-axis. Here is the region and one rotated disk:
The radius of the disk is \(r=x=\dfrac{1}{y}\). So the area is \(A=\pi r^2=\dfrac{\pi}{y^2}\) and the volume is \[ V=\int_1^4 \dfrac{\pi}{y^2}\,dy =\left[-\,\dfrac{\pi}{y}\right]_1^4 =-\,\dfrac{\pi}{4}+\pi=\dfrac{3\pi}{4} \]
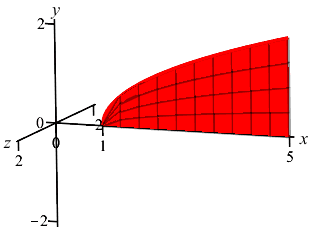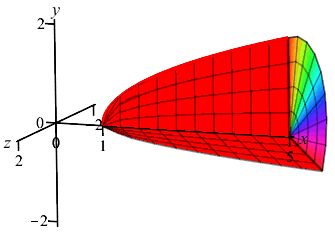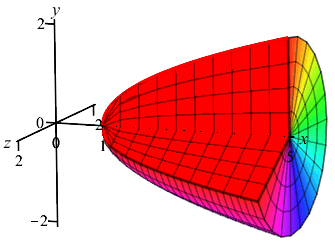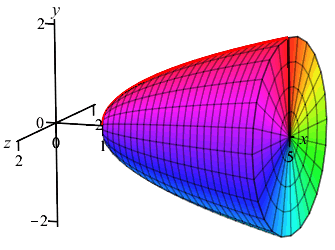
Find the volume of the solid of revolution obtained by rotating the region under the graph of \(y=\sqrt{x-1}\) for \(x \le 5\) about the \(x\)-axis.
\(V=8\pi\)
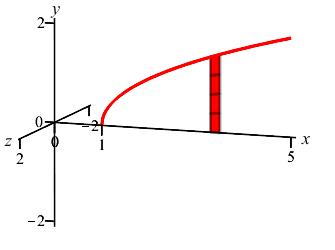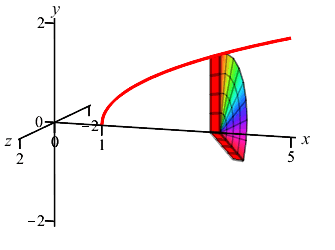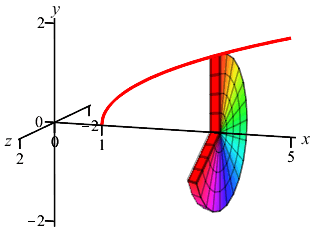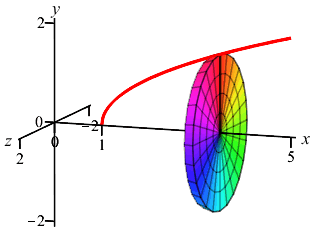
Since \(y\) is a function of \(x\), we chop up the \(x\)-axis, draw a vertical Riemann sum rectangle and see it rotates into a disk as shown.
With \(a=1\), \(b=5\) and \(r=y=\sqrt{x-1}\), the volume is \[\begin{aligned} V&=\pi\int_1^5 \sqrt{x-1}^2\,dx =\pi\int_1^5 (x-1)\,dx \\ &=\pi\left[\dfrac{x^2}{2}-x\right]_1^5 =8\pi \end{aligned}\]