13. Volume
Recall: The Volume of a Solid computed using Thin Disks is \[ V=\int_a^b \pi f(x)^2\,dx \qquad \text{or} \qquad V=\int_a^b \pi f(y)^2\,dy \]
c1a. Volume using Thin Disks - Example 1
We start with two examples which could also be computed from high school geometry.
Find the volume of the cone obtained by rotating the region under the straight line \(y=x\) between \(x=0\) and \(x=1\) around the \(x\)-axis.
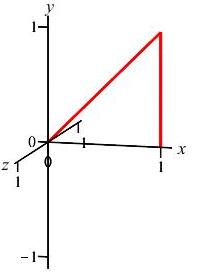
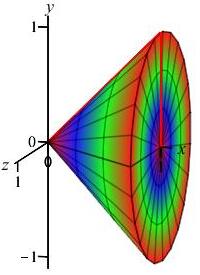
We draw the line \(y=x\) between \(x=0\) and \(x=1\) and one Riemann sum rectangle. We rotate the rectangle and see it sweeps out a disk.
We apply the disk formula, with \(a=0\) and \(b=1\) to get the volume: \[ V=\pi\int_0^1 x^2\,dx =\left.\pi\dfrac{x^3}{3}\right|_0^1 =\dfrac{\pi}{3} \]
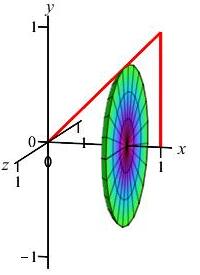
This volume could also have been computed from high school geometry as \(V=\dfrac{1}{3}\pi r^2h =\dfrac{1}{3}\pi(1)^2(1) =\dfrac{\pi}{3}\).
Find the volume of a sphere of radius \(2\), regarded as the solid of revolution of the region bounded by a semicircle of radius \(2\) rotated about the \(x\)-axis.
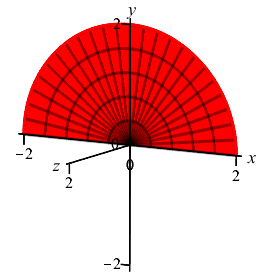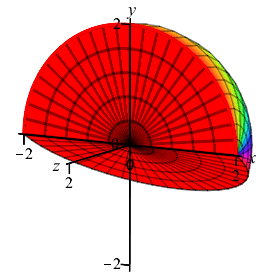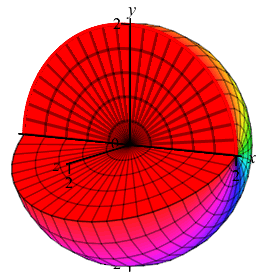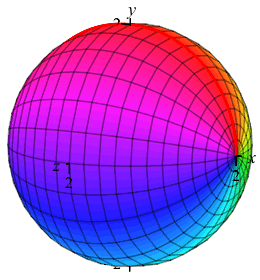
\(V=\dfrac{32}{3}\pi\).
The (upper) semicircle satisfies the equation \(y=\sqrt{4-x^2}\). Applying the formula for the volume of revolution using disks with \(a=-2\) and \(b=2\), we obtain \[\begin{aligned} V&=\int_{-2}^2 \pi\left(\sqrt{4-x^2}\right)^2\,dx \\ &=\pi\int_{-2}^2 (4-x^2)\,dx =\pi\left[4x-\dfrac{x^3}{3}\right]_{-2}^2 \\ &=\pi\left(8-\dfrac{8}{3}\right)-\pi\left(-8+\dfrac{8}{3}\right) =\dfrac{32}{3}\pi \end{aligned}\]
Again there is agreement with the classical formula. From geometry, we know that the volume of a sphere of radius \(r=2\) is \(V=\dfrac{4}{3}\pi r^3 =\dfrac{4}{3}\pi 2^3=\dfrac{32}{3}\pi\).
The agreement between the results of the integral formulas and the geometry formulas gives us a little confidence in it. However, the integral formula for volume is more powerful than a handbook of volume formulas.