19. Properties of Graphs
d. Second Derivative Information
2. Maxima & Minima and the Second Derivative Test
We previously looked at how to identify local mimima and local maxima using the First Derivative Test. While the First Derivative Test will always identify the local mimima and maxima, it is frequently easier to to use the Second Derivative Test:
Assume \(f(x)\) is twice differentiable on the interval \((a,b)\). Let \(c\)
be a point in \((a,b)\) where \(f'(c)=0\).
If \(f''(c) \gt 0\), then \((c,f(c))\) is a local minimum.
If \(f''(c) \lt 0\), then \((c,f(c))\) is a local maximum.
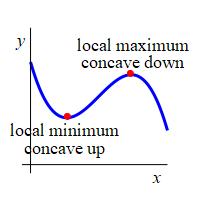
The condition \(f'(c)=0\) says the tangent line is horizontal at \(x=c\).
The condition \(f''(c) \gt 0\) says the curve is bending up at \(x=c\),
and so stays above the tangent line. So \(x=c\) is the location of a
local minimum.
The condition \(f''(c) \lt 0\) says the curve is bending down at \(x=c\),
and so stays below the tangent line. So \(x=c\) is the location of a
local maximum.
So to find the minima and maxima of \(f(x)\), we find the critical points \(x=c\) where \(f'(c)=0\) and compute the value of \(f''(c)\). If \(f''(c) \gt 0\), the curve is concave up at \(c\) and so \(c\) is a local minimum. If \(f''(c) \lt 0\), the curve is concave down at \(c\) and so \(c\) is a local maximum.
Find the local minima and local maxima of the function \(f(x)=\dfrac{x^4-39x^2-108}{3x}\) but using the Second Derivative Test.
In the example on the
previous three pages we found the first and second derivatives are:
\[\begin{aligned}
f'(x)&=\dfrac{(x^2-4)(x^2-9)}{x^4} \\
f''(x)&=\dfrac{2(x^2-6)(x^2+6)}{x^3}
\end{aligned}\]
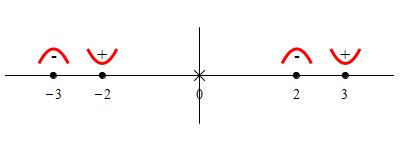
So the derivative is \(0\) at \(x=\pm2\) or \(x=\pm3\) and
is undefined at \(x=0\) which are the critical points. However, \(x=0\) is
also a point at which the function is undefined; so it cannot be a minimum
or maximum. We evaluate the second derivative at each of the other critical
points:
\[\begin{aligned}
f''(-3)&=\dfrac{2(9-6)(9+6)}{-27}=-\,\dfrac{10}{3} \lt 0&
f''(3)&=\dfrac{2(9-6)(9+6)}{27}=\dfrac{10}{3} \gt 0 \\
f''(-2)&=\dfrac{2(4-6)(4+6)}{-8}=5 \gt 0&
f''(2)&=\dfrac{2(4-6)(4+6)}{8}=-5 \lt 0
\end{aligned}\]
So there are local maxima at \(x=-3\) and \(x=2\) and
local minima at \(x=-2\) and \(x=3\) as shown on the numberline:
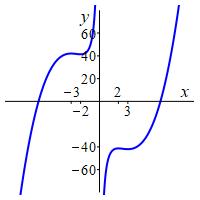
These are confirmed in the plot.
If \(f''(c)=0\), the test FAILS! Further, we cannot say the point is a horizontal inflection point! It may still be a local minimum or maximum! The test just fails. We need to fall back on the First Derivative Test to distinguish between local minimum, local maximum or horizontal inflection point. This happens in the next exercise.
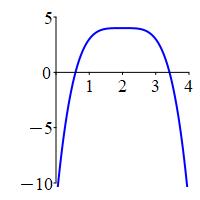
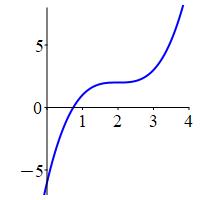
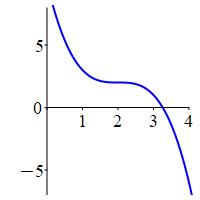
But first, here are the plots of \(4\) functions,
all of which have \(f'(2)=0\) — so \(x=2\) is a critical point, and
all of which have \(f''(2)=0\) — so the Second Derivative Test fails,
but one is a minimum, one is a maximum and two are horizontal
inflection points:
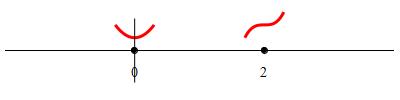
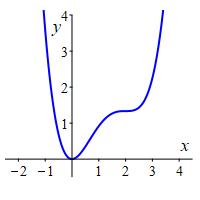
Find the local minima, local maxima and horizontal inflection points of the function \(f(x)=\dfrac{1}{4}x^4-\dfrac{4}{3}x^3+2x^2\) but using the Second Derivative Test.
\(f(x)\) has a local minimum at \(x=0\) and a horizontal inflection point
at \(x=2\).
In exercises on
three previous pages, we found the first and second derivatives are:
\[\begin{aligned}
f'(x)&=x(x-2)^2 \\
f''(x)&=(3x-2)(x-2)
\end{aligned}\]
So the critical points are \(x=0\) and \(x=2\) and the secondary critical
points are \(x=\dfrac{2}{3}\) and \(x=2\). To apply the Second Derivative
Test, we evaluate the second derivative at each critical point:
\[
f''(0)=(0-2)(0-2)=4 \qquad
f''(2)=\left(3\cdot2-2\right)(2-2)=0
\]
Since \(f''(0) \gt 0\), the function is concave up at \(x=0\) and so is a
local minimum. Since \(f''(2)=0\), the Second Derivative Test fails and
we turn to the First Derivative Test.
Since \(f'(x)=x(x-2)^2\) is positive for all \(x \gt 0\), the function is
increasing on both sides of \(x=2\) which is therefore a horizontal
inflection point. The local minimum and the inflection point are indicated
on the number line:

In the plot, we see the function has a minimum at \((0,0)\) where it is concave up and a horizontal inflection point at \((2,\dfrac{4}{3})\) where the function is increasing on both sides.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum