19. Properties of Graphs
e. Curve Sketching
We now put everything together to get an idea about how to roughly graph a function. Some information will be redundant. It is best to learn by example.
For the function \(f(x)=\dfrac{1}{6}x^6-\dfrac{2}{5}x^5+\dfrac{1}{4}x^4\), find the intercepts, asymptotes, intervals where the function is increasing, decreasing, concave up and concave down, local minima, local maxima and inflection points. Then plot it.
- \(y\)-intercept: The \(y\)-intercept is at \(f(0)=0\).
- \(x\)-intercepts: To find the \(x\)-intercepts, we try factoring the function. We first write: \[ f(x)=\dfrac{1}{60}x^4(10x^2-24x+15) \] To find the zeros of the second factor, we use the quadratic formula: \[ x=\dfrac{24\pm\sqrt{4\cdot144-4\cdot150}}{20} =\dfrac{12\pm i\sqrt{6}}{10} \] Since the solutions are complex, there are no real solutions to the quadratic factor and the the only \(x\)-intercept is \(x=0\). Further, since \(f(-1)=\dfrac{49}{60}\) and \(f(1)=\dfrac{1}{60}\), the function is always positive except at \(x=0\).
- vertical asymptotes: The function is defined for all \(x\). So there are no vertical asymptotes.
- horizontal and slant asymptotes: Since the function looks like \(\dfrac{1}{6}x^6\) for large \(x\), there are no horizontal or slant asymptotes.
-
increasing and decreasing:
The derivative is:
\[
f'(x)=x^5-2x^4+x^3=x^3(x^2-2x+1)=x^3(x-1)^2
\]
So the critical points are at \(x=0\) and \(x=1\). The value at the new
point is:
\[
f(1)=\dfrac{1}{6}-\dfrac{2}{5}+\dfrac{1}{4}=\dfrac{1}{60}
\]
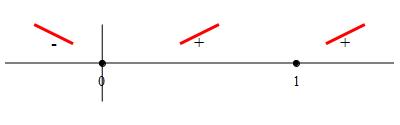
We plot these on a number line.
 Then we evaluate the derivative at a point in each interval to see if it is
positive or negative.
\[\begin{aligned}
f'(-1)&=-4 \lt 0 \\
f'(.5)&=.125(.5)^2 \gt 0 \\
f'(2)&=8 \gt 0
\end{aligned}\]
So the function is decreasing on \((-\infty,0)\) and increasing on
\((0,\infty)\). Notice the derivative is \(0\) at \(x=1\) but the function
continues to increase on both sides.
Then we evaluate the derivative at a point in each interval to see if it is
positive or negative.
\[\begin{aligned}
f'(-1)&=-4 \lt 0 \\
f'(.5)&=.125(.5)^2 \gt 0 \\
f'(2)&=8 \gt 0
\end{aligned}\]
So the function is decreasing on \((-\infty,0)\) and increasing on
\((0,\infty)\). Notice the derivative is \(0\) at \(x=1\) but the function
continues to increase on both sides.
-
concavity and inflection points:
The second derivative is:
\[
f''(x)=5x^4-8x^3+3x^2=x^2(5x^2-8x+3)=x^2(5x-3)(x-1)
\]
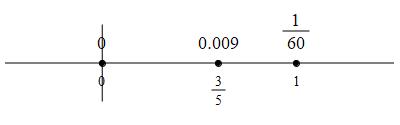
So the secondary critical points are \(x=0\), \(x=\dfrac{3}{5}\) and \(x=1\).
The value at the new point is:
\[
f\left(\dfrac{3}{5}\right)
=\dfrac{1}{6}\left(\dfrac{3}{5}\right)^6
-\dfrac{2}{5}\left(\dfrac{3}{5}\right)^5
+\dfrac{1}{4}\left(\dfrac{3}{5}\right)^4
=\dfrac{567}{62500}
\approx0.009
\]
We plot these on a number line.
 Then we evaluate the second derivative at a point in each interval to see
if it is positive or negative.
\[\begin{aligned}
f''(-1)&=(1)(-8)(-2)=16 \gt 0&
f''(.5)&=(.25)(-.5)(-.5) \gt 0 \\
f''(.75)&=.75^2(.75)(-.25) \lt 0&
f''(2)&=4(7)(1)=28 \gt 0
\end{aligned}\]
So the function is concave up on \((-\infty,\dfrac{3}{5})\), concave down on
\((\dfrac{3}{5},1)\) and concave up again on \((1,\infty)\).
Then we evaluate the second derivative at a point in each interval to see
if it is positive or negative.
\[\begin{aligned}
f''(-1)&=(1)(-8)(-2)=16 \gt 0&
f''(.5)&=(.25)(-.5)(-.5) \gt 0 \\
f''(.75)&=.75^2(.75)(-.25) \lt 0&
f''(2)&=4(7)(1)=28 \gt 0
\end{aligned}\]
So the function is concave up on \((-\infty,\dfrac{3}{5})\), concave down on
\((\dfrac{3}{5},1)\) and concave up again on \((1,\infty)\).
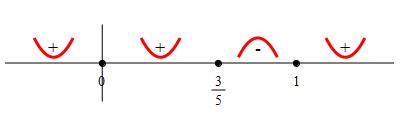 Notice the second derivative is \(0\) at \(x=0\) but the function continues
to be concave up on both sides. So there are inflection points only at
\(x=\dfrac{3}{5}\) and \(x=1\).
Notice the second derivative is \(0\) at \(x=0\) but the function continues
to be concave up on both sides. So there are inflection points only at
\(x=\dfrac{3}{5}\) and \(x=1\).
-
local minima, local maxima and horizontal inflection points:
We evaluate the second derivative at each critical point, \(x=0\) and
\(x=1\):
\[
f''(0)=0^2(0-3)(0-1)=0 \qquad
f''(1)=1(5-3)(0)=0
\]
So the Second Derivative Test fails at both critical points. We turn to
the First Derivative Test. The function decreases on \((-\infty,0)\)
and increases on \((0,1)\) and \((1,\infty)\). So there is a local
minimum at \(x=0\) and a horizontal inflection point at \(x=1\).
There is no local maximum.

- plot: (Click on each button.)
- We first put a dot at \((0,0)\) which is the only .
- Next, we put a horizontal line at the \((0,0)\) and \((1,1/60)\).
- Now, we put an upward arc at the \((0,0)\).
- Then, we put wiggles at the \(\left(\dfrac{3}{5},\dfrac{567}{62500}\right)\approx(.6,.009)\) and \(\left(1,\dfrac{1}{60}\right)\approx(1,.016\bar{6})\), noticing that the one at \(x=1\) is horizontal and the one at \(x=\dfrac{3}{5}\) is a point where the function is increasing and switches from concave up to concave down.
- Finally, we the dots making sure the function is decreasing for \(x \lt 0\), increasing for \(x \gt 0\), concave up for \(x \lt \dfrac{3}{5}\), concave down for \(\dfrac{3}{5} \lt x \lt 1\) and concave up for \(x \gt 1\).
- Your sketch does not need to be exact.
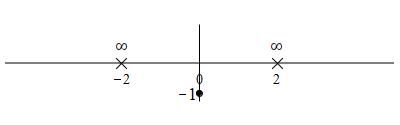
For the function \(f(x)=\dfrac{x^2+4}{x^2-4}\), find the intercepts, asymptotes, intervals where the function is increasing, decreasing, concave up and concave down, local minima, local maxima and inflection points. Then plot it.
- \(y\)-intercept: The \(y\)-intercept is at \(f(0)=\dfrac{+4}{-4}=-1\).
- \(x\)-intercepts: Since the numerator, \(x^2+4\), is never \(0\), there are no \(x\)-intercepts.
-
vertical asymptotes:
The denominator, \(x^2-4\), is \(0\) at \(x=\pm2\). So these are the
vertical asymptotes. We plot the location of the intercept and vertical
asymptotes:
 We rewrite the function as
\[
f(x)=\dfrac{x^2+4}{(x+2)(x-2)}
\]
and compute four limits to determine how the curve approaches the vertical
asymptotes:
\[\begin{aligned}
\lim_{x\to-2^-}\dfrac{x^2+4}{(x+2)(x-2)}
&=``\dfrac{4+4}{(-2^-+2)(-2^--2)}"=``\dfrac{8}{(0^-)(-4)}"=\infty \\
\lim_{x\to-2^+}\dfrac{x^2+4}{(x+2)(x-2)}
&=``\dfrac{4+4}{(-2^++2)(-2^+-2)}"=``\dfrac{8}{(0^+)(-4)}"=-\infty \\
\lim_{x\to2^-}\dfrac{x^2+4}{(x+2)(x-2)}
&=``\dfrac{4+4}{(2^-+2)(2^--2)}"=``\dfrac{8}{(4)(0^-)}"=-\infty \\
\lim_{x\to2^+}\dfrac{x^2+4}{(x+2)(x-2)}
&=``\dfrac{4+4}{(2^++2)(2^+-2)}"=``\dfrac{8}{(4)(0^+)}"=\infty
\end{aligned}\]
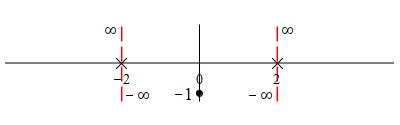
So the asymptote at \(x=-2\) is approached up-down while the asymptote at
\(x=2\) is approached down-up.
We rewrite the function as
\[
f(x)=\dfrac{x^2+4}{(x+2)(x-2)}
\]
and compute four limits to determine how the curve approaches the vertical
asymptotes:
\[\begin{aligned}
\lim_{x\to-2^-}\dfrac{x^2+4}{(x+2)(x-2)}
&=``\dfrac{4+4}{(-2^-+2)(-2^--2)}"=``\dfrac{8}{(0^-)(-4)}"=\infty \\
\lim_{x\to-2^+}\dfrac{x^2+4}{(x+2)(x-2)}
&=``\dfrac{4+4}{(-2^++2)(-2^+-2)}"=``\dfrac{8}{(0^+)(-4)}"=-\infty \\
\lim_{x\to2^-}\dfrac{x^2+4}{(x+2)(x-2)}
&=``\dfrac{4+4}{(2^-+2)(2^--2)}"=``\dfrac{8}{(4)(0^-)}"=-\infty \\
\lim_{x\to2^+}\dfrac{x^2+4}{(x+2)(x-2)}
&=``\dfrac{4+4}{(2^++2)(2^+-2)}"=``\dfrac{8}{(4)(0^+)}"=\infty
\end{aligned}\]
So the asymptote at \(x=-2\) is approached up-down while the asymptote at
\(x=2\) is approached down-up.
-
horizontal and slant asymptotes:
We take the limits as \(x\to\pm\infty\):
\[\begin{aligned}
\lim_{x\to-\infty}\dfrac{x^2+4}{x^2-4}=1 \\
\lim_{x\to\infty}\dfrac{x^2+4}{x^2-4}=1
\end{aligned}\]
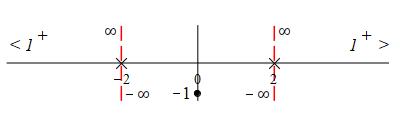
So the horizontal asymptote is \(y=1\) at both \(-\infty\) and \(\infty\).
To see if these asymptotes are approached from above or below, we look at
the sign of
\[
f(x)-1=\dfrac{x^2+4}{x^2-4}-1=\dfrac{(x^2+4)-(x^2-4)}{x^2-4}
=\dfrac{8}{x^2-4}
\]
This is positive as \(x\to\pm\infty\). So the asymptotes are approached
from above.
-
increasing and decreasing:
The derivative of \(f(x)=\dfrac{x^2+4}{x^2-4}\) is:
\[
f'(x)=\dfrac{(x^2-4)2x-(x^2+4)2x}{(x^2-4)^2}=\dfrac{-16x}{(x^2-4)^2}
\]
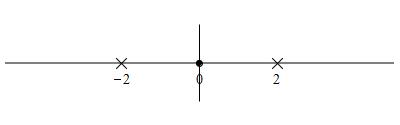
So the critical points are \(x=0\) and \(x=\pm2\). We plot these on a number
line.
 Notice that these happen to be the in the same locations as the intercept
and the vertical asymptotes. Next, we evaluate the derivative at a point
in each interval to see if it is positive or negative.
\[\begin{aligned}
f'(-3)&=\dfrac{48}{(9-4)^2} \gt 0&
f'(3)&=\dfrac{-48}{(9-4)^2} \lt 0 \\
f'(-1)&=\dfrac{16}{(1-4)^2} \gt 0&
f'(1)&=\dfrac{-16}{(1-4)^2} \lt 0
\end{aligned}\]
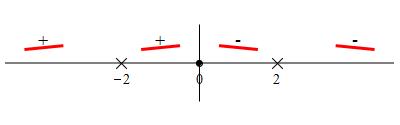
So the function is increasing on \((-\infty,-2)\) and \((-2,0)\) and
decreasing on \((0,2)\) and \((2,\infty)\).
Notice that these happen to be the in the same locations as the intercept
and the vertical asymptotes. Next, we evaluate the derivative at a point
in each interval to see if it is positive or negative.
\[\begin{aligned}
f'(-3)&=\dfrac{48}{(9-4)^2} \gt 0&
f'(3)&=\dfrac{-48}{(9-4)^2} \lt 0 \\
f'(-1)&=\dfrac{16}{(1-4)^2} \gt 0&
f'(1)&=\dfrac{-16}{(1-4)^2} \lt 0
\end{aligned}\]
So the function is increasing on \((-\infty,-2)\) and \((-2,0)\) and
decreasing on \((0,2)\) and \((2,\infty)\).
-
concavity and inflection points:
The second derivative of \(f(x)=\dfrac{x^2+4}{x^2-4}\) is:
\[\begin{aligned}
f''(x)&=\dfrac{(x^2-4)^2(-16)-(-16x)2(x^2-4)2x}{(x^2-4)^4} \\
&=\dfrac{(x^2-4)(-16)-(-16x)4x}{(x^2-4)^3} \\
&=\dfrac{16(3x^2+4)}{(x^2-4)^3}
\end{aligned}\]
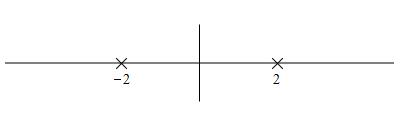
Since the numerator is never \(0\), the only secondary critical points are the
vertical asymptotes \(x=\pm2\). We, once again, plot these on a number line.
 Next, we evaluate the second derivative at a point in each interval to see
if it is positive or negative.
\[\begin{aligned}
f''(-3)&=\dfrac{16(27+4)}{(9-4)^3} \gt 0&
f''(3)&=\dfrac{16(27+4)}{(9-4)^3} \gt 0 \\
f''(0)&=\dfrac{16(0+4)}{(0-4)^3} \lt 0
\end{aligned}\]
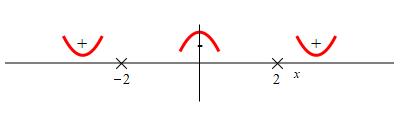
So the function is concave up on \((-\infty,-2)\), concave down on
\((-2,2)\) and concave up again on \((2,\infty)\). Notice the
second derivative is never \(0\). So there are no inflection points.
Next, we evaluate the second derivative at a point in each interval to see
if it is positive or negative.
\[\begin{aligned}
f''(-3)&=\dfrac{16(27+4)}{(9-4)^3} \gt 0&
f''(3)&=\dfrac{16(27+4)}{(9-4)^3} \gt 0 \\
f''(0)&=\dfrac{16(0+4)}{(0-4)^3} \lt 0
\end{aligned}\]
So the function is concave up on \((-\infty,-2)\), concave down on
\((-2,2)\) and concave up again on \((2,\infty)\). Notice the
second derivative is never \(0\). So there are no inflection points.
-
local minima, local maxima and horizontal inflection points:
The critical points are \(x=0\) and \(x=\pm2\). However, \(x=\pm2\) are
vertical asymptotes. So they cannot be local maxima nor minima.
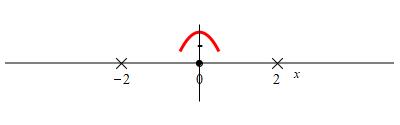
We evaluate the second derivative \(x=0\):
\[
f''(0)=\dfrac{16(0+4)}{(0-4)^3}=-1 \lt 0
\]
So the Second Derivative Test says\((0,-1)\) is a local minimum. There are
no local maxima.
- plot: (Click on each button.)
- We first put a dot at the \((0,-1)\). There are no \(x\)-intercepts.
- Now, we put an downward arc at the \((0,-1)\).
- Then, we put dashed lines at the \(x=-2\) and \(x=2\), and at the \(y=1\).
- Next, we add curved lines next to the to indicate that \(x=-2\) is approached up-down, \(x=2\) is approached down-up and \(y=1\) is approached from above at both \(\pm\infty\).
- Finally, we making sure the function is increasing and concave up for \(x \lt -2\), increasing and concave down for \(-2 \lt x \lt 0\), decreasing and concave down for \(0 \lt x \lt 2\) and decreasing and concave up for \(x \gt 2\).
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum