19. Properties of Graphs

c. First Derivative Information

2. Maxima & Minima and the First Derivative Test

A function \(f(x)\) has a local minimum at a point \((c,f(c))\) if there is an interval \((a,b)\) containing \(c\) for which \(f(c)\) is the smallest value of \(f(x)\) in the interval. Then \(c\) is called the location of the minimum and \(f(c)\) is called the value of the minimum.
A function \(f(x)\) has a local maximum at a point \((c,f(c))\) if there is an interval \((a,b)\) containing \(c\) for which \(f(c)\) is the largest value of \(f(x)\) in the interval. Then \(c\) is called the location of the maximum and \(f(c)\) is called the value of the maximum.

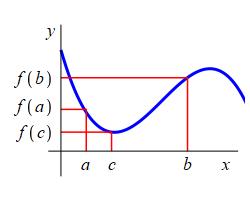
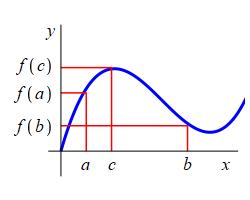def_min   def_max  Local Minimum        Local Maximum

Assume \(f(x)\) is differentiable on the interval \((a,b)\).
If \(f'(x) \lt 0\) for all \(x\) in \((a,c)\) and \(f'(x) \gt 0\) for all \(x\) in \((c,b)\), then \(f(c)\) is a local minimum.
If \(f'(x) \gt 0\) for all \(x\) in \((a,c)\) and \(f'(x) \lt 0\) for all \(x\) in \((c,b)\), then \(f(c)\) is a local maximum.

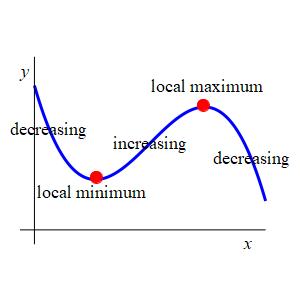
thm_1st_test

The conditions \(f'(x) \lt 0\) for all \(x\) in \((a,c)\) and \(f'(x) \gt 0\) for all \(x\) in \((c,b)\) say \(f\) is decreasing on the left of \(c\) and increasing on the right. So \(f(c)\) is the smallest value.
Similarly, the conditions \(f'(x) \gt 0\) for all \(x\) in \((a,c)\) and \(f'(x) \lt 0\) for all \(x\) in \((c,b)\) say \(f\) is increasing on the left of \(c\) and decreasing on the right. So \(f(c)\) is the largest value.

So to find the minima and maxima of \(f(x)\), we find the critical points \(x=c\) where \(f'(c)=0\) (or where \(f(x)\) exists but \(f'(x)\) does not) and check the intervals on each side to see if \(f'(x) \gt 0\) or \(f'(x) \lt 0\). If the sign of the derivative changes, then \(x=c\) is a minima or a maxima as determined by the theorem.

Find the local minima and local maxima of the function \(f(x)=\dfrac{x^4-39x^2-108}{3x}\).

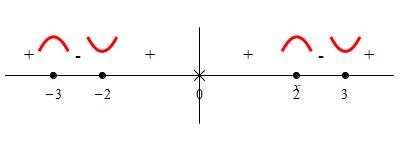
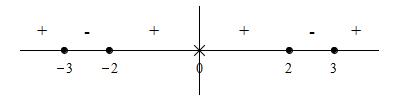In the example on the previous page we found the \(f(x)\) is increasing on the intervals \((-\infty,-3)\), \((-2,0)\), \((0,2)\) and \((3,\infty)\), while it is decreasing on \((-3,-2)\), and \((2,3)\) as summarized on the number line: eg_x^4-39x^2-108_3x_number_line_deriv_incrdecr Based on the signs of the derivative, we indicate the local maxima and minima of \(f(x)\): ex_x^4-39x^2-108_3x_number_line_deriv_maxmin We compute the function values: \[\begin{aligned} f(-3)&=\dfrac{81-39\cdot9-108}{-9}=42& f(-2)&=\dfrac{16-39\cdot4-108}{-6}=\dfrac{124}{3} \\ f(2)&=\dfrac{16-39\cdot4-108}{6}=-\,\dfrac{124}{3}& f(3)&=\dfrac{81-39\cdot9-108}{9}=-42 \end{aligned}\]

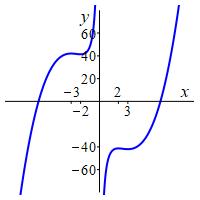
So there are local maxima at \((-3,43)\) and \((2,-\,\dfrac{124}{3})\) and local minima at \((-2,\dfrac{124}{3})\) and \((3,-43)\) as confirmed in the plot. The function also has a vertical asymptote at \(x=0\).

eg_x^4-39x^2-108_3x

An isolated point \(x=c\) where \(f'(c)=0\) but \(f'(x)\) does not change sign on the two sides cannot be a minimum or a maximum. it is called a horizontal inflection point. This occurs in the next example. We postpone a more detailed discussion of inflection points until after the discussion of the Second Derivative Test on the page after next.

Find the local minima and local maxima of the function \(f(x)=\dfrac{1}{4}x^4-\dfrac{4}{3}x^3+2x^2\).

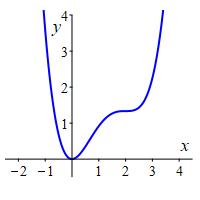
\(f(x)\) has a local minimum at \(x=0\). There are no local maxima. ex_x^4_4-4x^3_3+2x^2_number_line_deriv_maxmin

In an exercise on the previous page, we found the derivative is \(f'(x)=x(x-2)^2\), the critical points are \(x=0\) and \(x=2\) and the function is decreasing on \((-\infty,0)\) and increasing on \((0,\infty)\). Further, \(x=2\) is a horizontal inflection point. Since it is decreasing to the left of \(x=0\) and increasing to the right, \(f(x)\) has a local minimum at \(x=0\). There are no local maxima. ex_x^4_4-4x^3_3+2x^2_number_line_deriv_maxmin

In the plot, we see the local minimum at \(x=0\) and a horizontal inflection point at \((2,\dfrac{4}{3})\).

ex_x^4_4-4x^3_3+2x^2

© MYMathApps

Supported in part by NSF Grant #1123255