19. Properties of Graphs
c. First Derivative Information
1. Increasing & Decreasing
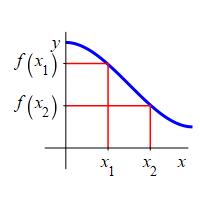
A function \(f(x)\) is increasing on an interval \([a,b]\) if for all \(x_1\) and \(x_2\) with \(a \le x_1 \lt x_2 \le b\), we have \[ f(x_1) \lt f(x_2) \] A function \(f(x)\) is decreasing on an interval \([a,b]\) if for all \(x_1\) and \(x_2\) with \(a \le x_1 \lt x_2 \le b\), we have \[ f(x_1) \gt f(x_2) \]
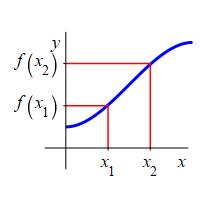
 Increasing
Decreasing
Increasing
Decreasing
If \(f'(x) \gt 0\) for all \(x\) in \([a,b]\), then \(f(x)\) is
increasing on the interval \([a,b]\).
If \(f'(x) \lt 0\) for all \(x\) in \([a,b]\), then \(f(x)\) is
decreasing on the interval \([a,b]\).
Let \(a \le x_1 \lt x_2 \le b\). By the Mean Value Theorem applied to \(f(x)\) on the interval \([x_1,x_2]\), we know there is a number \(c\) in \([x_1,x_2]\) such that \[ f(x_2)=f(x_1)+f'(c)(x_2-x_1) \] Since \(f'(c) \gt 0\) and \(x_2 \gt x_1\), we conclude \[ f(x_2) \gt f(x_1) \] which says \(f(x)\) is increasing.
The proof for decreasing is the same except for two changes in inequalities. Try doing it yourself.
So to find the intervals where \(f(x)\) is increasing and decreasing, we find the points where the derivative, \(f'(x)\), is \(0\) or undefined, plot them on a number line and test a point in each interval to find if \(f'(x)\) is positive or negative in that interval.
The critical points of a function \(f(x)\) are the values of \(x\) at which \(f'(x)\) is \(0\) or undefined.
Find the intervals where \(f(x)=\dfrac{x^4-39x^2-108}{x}\) is increasing or decreasing.
To compute the derivative of \(f(x)\), we could use the Quotient Rule.
However, it is easier to first simplify the function:
\[\begin{aligned}
f(x)&=x^3-39x-\dfrac{108}{x} \\
f'(x)&=3x^2-39+\dfrac{108}{x^2} \\
&=3\left(x^2-13+\dfrac{36}{x^2}\right) \\
&=3\frac{x^4-13x^2+36}{x^2}\\
&=3\frac{(x^2-4)(x^2-9)}{x^2}\\
\end{aligned}\]
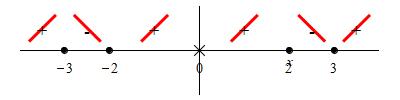
So the derivative is \(0\) at \(x=\pm2\) or \(x=\pm3\) and
is undefined at \(x=0\). We plot these critical points on a number line:
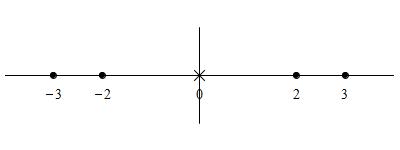 We test a point in each interval to see if \(f'(x)\) is positive or negative
in each the \(6\) intervals.
\[\begin{aligned}
f'(-4)&=3\dfrac{(16-4)(16-9)}{4^2} \gt 0
& f'(4)&=3\dfrac{(16-4)(16-9)}{x^2} \gt 0 \\
f'(-2.5)&=3\dfrac{(6.25-4)(6.25-9)}{2.5^2} \lt 0 \quad
& f'(2.5)&=3\dfrac{(6.25-4)(6.25-9)}{2.5^2} \lt 0 \\
f'(-1)&=3\dfrac{(1-4)(1-9)}{1} \gt 0
& f'(1)&=3\dfrac{(1-4)(1-9)}{1} \gt 0
\end{aligned}\]
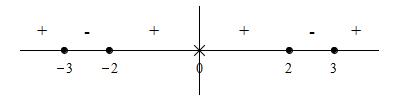
So \(f'(x)\) is positive on the intervals \((-\infty,-3)\),
\((-2,0)\), \((0,2)\) and \((3,\infty)\), while it is
negative on \((-3,-2)\), and \((2,3)\).
We summarize these results on the number line:
We test a point in each interval to see if \(f'(x)\) is positive or negative
in each the \(6\) intervals.
\[\begin{aligned}
f'(-4)&=3\dfrac{(16-4)(16-9)}{4^2} \gt 0
& f'(4)&=3\dfrac{(16-4)(16-9)}{x^2} \gt 0 \\
f'(-2.5)&=3\dfrac{(6.25-4)(6.25-9)}{2.5^2} \lt 0 \quad
& f'(2.5)&=3\dfrac{(6.25-4)(6.25-9)}{2.5^2} \lt 0 \\
f'(-1)&=3\dfrac{(1-4)(1-9)}{1} \gt 0
& f'(1)&=3\dfrac{(1-4)(1-9)}{1} \gt 0
\end{aligned}\]
So \(f'(x)\) is positive on the intervals \((-\infty,-3)\),
\((-2,0)\), \((0,2)\) and \((3,\infty)\), while it is
negative on \((-3,-2)\), and \((2,3)\).
We summarize these results on the number line:
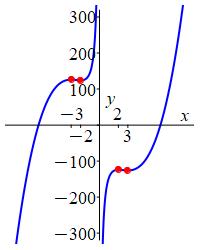
 Based on the signs of the derivative, we indicate the intervals where \(f(x)\)
is increasing and decreasing:
Based on the signs of the derivative, we indicate the intervals where \(f(x)\)
is increasing and decreasing:
The plot shows the four critical points, the four intervals where the function is increasing and the two intervals where it is decreasing.
An isolated point \(x=p\) where \(f(p)=0\) but \(f'(x)\) does not change sign on the two sides is part of a single interval where \(f\) is increasing or decreasing, as in the next exercise. Such a point is called a horizontal inflection point as will be discussed more on the next three pages.
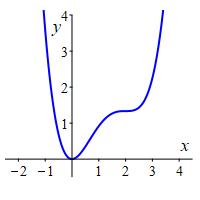
Find the intervals where \(f(x)=\dfrac{1}{4}x^4-\dfrac{4}{3}x^3+2x^2\) is increasing or decreasing. Further, identify any horizontal inflection points.
\(f(x)\) is decreasing on \((-\infty,0)\) and increasing on \((0,\infty)\).
Further, \(x=2\) is a horizontal inflection point within the interval
where \(f(x)\) is increasing.
The derivative is:
\[
f'(x)=x^3-4x^2+4x=x(x-2)^2
\]
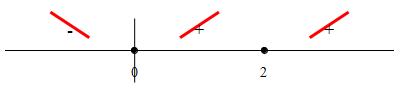
which is defined for all \(x\) and is \(0\) at \(x=0\) and \(x=2\).
So these are the critical points which we plot on a number line:
 We test a point in each interval to see where \(f'(x)\) is positive or
negative:
\[\begin{aligned}
f'(-1)&=(-1)(-1-2)^2=-9 \lt 0
& f'(1)&=(1)(1-2)^2=1 \gt 0 \\
f'(3)&=3(3-2)^2=3 \gt 0
\end{aligned}\]
So \(f'(x)\) is negative on \((-\infty,0)\) and positive on
\((0,2)\) and \((2,\infty)\). So the function is decreasing on
\((-\infty,0)\) and increasing on \((0,\infty)\). Notice that \(x=2\)
is a horizontal inflection point within the interval where it is increasing.
We add these results to the number line:
We test a point in each interval to see where \(f'(x)\) is positive or
negative:
\[\begin{aligned}
f'(-1)&=(-1)(-1-2)^2=-9 \lt 0
& f'(1)&=(1)(1-2)^2=1 \gt 0 \\
f'(3)&=3(3-2)^2=3 \gt 0
\end{aligned}\]
So \(f'(x)\) is negative on \((-\infty,0)\) and positive on
\((0,2)\) and \((2,\infty)\). So the function is decreasing on
\((-\infty,0)\) and increasing on \((0,\infty)\). Notice that \(x=2\)
is a horizontal inflection point within the interval where it is increasing.
We add these results to the number line:

In the plot, we see the function is decreasing for \(x \lt 0\) and increasing for \(x \gt 0\) with a horizontal inflection point at \(x=2\).
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum