19. Properties of Graphs

d. Second Derivative Information

1. Concave Up & Down

A function \(f(x)\) is concave up on an interval \([a,b]\) if for all \(x_1\) and \(x_2\) with \(a \le x_1 \lt x_2 \le b\), we have \[ f'(x_1) \lt f'(x_2) \] A function \(f(x)\) is concave down on an interval \([a,b]\) if for all \(x_1\) and \(x_2\) with \(a \le x_1 \lt x_2 \le b\), we have \[ f'(x_1) \gt f'(x_2) \]

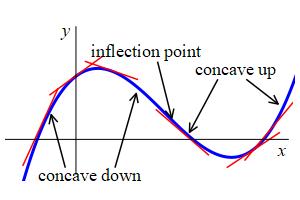
This says, the function is concave up if the slope increases as we move from left to right, or is bending upward. Similarly, the function is concave down if the slope decreases as we move from left to right, or is bending downward.

If \(f''(x) \gt 0\) for all \(x\) in \([a,b]\), then \(f(x)\) is concave up on the interval \([a,b]\).
If \(f''(x) \lt 0\) for all \(x\) in \([a,b]\), then \(f(x)\) is concave down on the interval \([a,b]\).

Let \(a \le x_1 \lt x_2 \le b\). By the Mean Value Theorem applied to \(f'(x)\) on the interval \([x_1,x_2]\), we know there is a number \(c\) in \([x_1,x_2]\) such that \[ f'(x_2)=f'(x_1)+f''(c)(x_2-x_1) \] Since \(f''(c) \gt 0\) and \(x_2 \gt x_1\), we conclude \[ f'(x_2) \gt f'(x_1) \] which says \(f(x)\) is concave up.

The proof for decreasing is the same except for two changes in inequalities. Try doing it yourself.

So to find the intervals where \(f(x)\) is concave up and down, we find the points where the second derivative, \(f''(x)\), is \(0\) or undefined, plot them on a number line and test a point in each interval to find if \(f''(x)\) is positive or negative in that interval.

The secondary critical points of a function \(f(x)\) are the values of \(x\) at which \(f''(x)\) is \(0\) or undefined.

An inflection point of a function \(f(x)\) is a point \(x=c\) at which the concavity changes, i.e. \(f''(c)=0\) and \(f''(x)\) changes sign on the two sides. The curve changes from bending one way to the other; it “flexes”. If, in addition, \(f'(c)=0\), then the tangent line is horizontal at \(c\) and so \(c\) is a horizontal inflection point.

Find the intervals where \(f(x)=\dfrac{x^4-39x^2-108}{3x}\) is concave up and down.

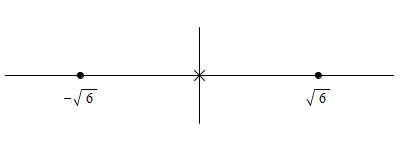
In the example on the two previous pages, we rewrote the function and computed the derivative: \[\begin{aligned} f(x)&=\dfrac{1}{3}x^3-13x-\dfrac{36}{x} \\ f'(x)&=x^2-13+\dfrac{36}{x^2} \end{aligned}\] So the second derivative is \[ f''(x)=2x-\dfrac{72}{x^3}=\dfrac{2x^4-72}{x^3}=\dfrac{2(x^2-6)(x^2+6)}{x^3} \] So the second derivative is \(0\) at \(x=\pm\sqrt{6}\) and is undefined at \(x=0\). We plot these secondary critical points on a number line: eg_x^4-39x^2-108_3x_number_line_2deriv_crit We test a point in each interval to see if \(f''(x)\) is positive or negative in each the \(4\) intervals. 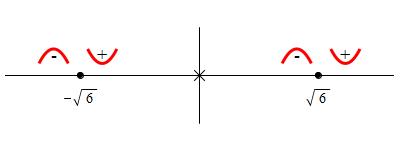\[\begin{aligned} f''(-3)&=\dfrac{2(9-6)(9+6)}{-27}=-\,\dfrac{10}{3} \lt 0 & f''(3)&=\dfrac{2(9-6)(9+6)}{27}=\dfrac{10}{3} \gt 0 \\ f''(-2)&=\dfrac{2(4-6)(4+6)}{-8}=5 \gt 0 \quad & f''(2)&=\dfrac{2(4-6)(4+6)}{8}=-5 \lt 0 \end{aligned}\] We add these signs and the concavity to the numberline: eg_x^4-39x^2-108_3x_number_line_2deriv_signs

So \(f(x)\) is concave down on the intervals \((-\infty,-\sqrt{6})\) and \((0,\sqrt{6})\), while it is concave up on \((-\sqrt{6},0)\) and \((\sqrt{6},\infty)\). We confirm these in the graph.

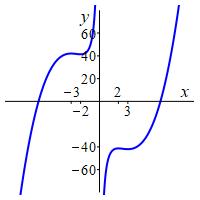
A point where \(f''(p)=0\) but \(f''(x)\) does not change sign on the two sides is not an inflection point. It is part of an interval of (up or down) concavity.

Find the intervals where \(f(x)=\dfrac{1}{4}x^4-\dfrac{4}{3}x^3+2x^2\) is concave up or down.

\(f(x)\) is concave up on \(\left(-\infty,\dfrac{2}{3}\right)\), concave down on \(\left(\dfrac{2}{3},2\right)\) and concave up again on \((2,\infty)\). ex_x^4_4-4x^3_3+2x^2_number_line_2deriv_updn

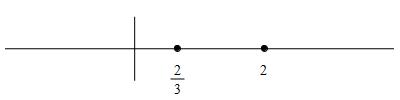
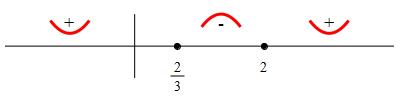
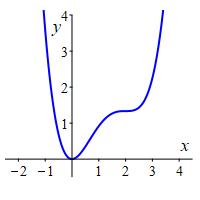
In exercises on two previous pages, we found the derivative is \(f'(x)=x^3-4x^2+4x\). So the second derivative is: \[ f''(x)=3x^2-8x+4=(3x-2)(x-2) \] So the secondary critical points are \(x=\dfrac{2}{3}\) and \(x=2\). If you can't easily factor it, use the quadratic formula: \[ x=\dfrac{8\pm\sqrt{64-48}}{6}=\dfrac{8\pm4}{6}=2,\dfrac{2}{3} \] We plot these points on a number line: ex_x^4_4-4x^3_3+2x^2_number_line_2deriv_crit We test a point in each interval to see where the second derivative is positive or negative: \[\begin{aligned} f''(0)&=(-2)(-2)=4 \gt 0 & f''(1)&=(3-2)(1-2)=-1 \lt 0 \\ f''(3)&=(9-2)(3-2)=7 \gt 0 \end{aligned}\] So \(f(x)\) is concave up on \(\left(-\infty,\dfrac{2}{3}\right)\), concave down on \(\left(\dfrac{2}{3},2\right)\) and concave up again on \((2,\infty)\). We add these signs and the concavity to the numberline: ex_x^4_4-4x^3_3+2x^2_number_line_2deriv_updn

In the plot, we see \(f(x)\) is concave up on \(\left(-\infty,\dfrac{2}{3}\right)\), concave down on \(\left(\dfrac{2}{3},2\right)\) and concave up again on \((2,\infty)\).

19. Properties of Graphs

d. Second Derivative Information

1. Concave Up & Down

Heading