5. Derivatives and Tangent Lines

Exercises

a. Derivative at a Point

1

2

1. E.T. propels a projectile straight up into the air through the power of telekinesis. The projectile's initial speed is \(400\) ft/sec, its height after \(t\) seconds is given by the function \(y(t)=400t-25t^2\).

   1. Find the average velocity, \(v\) between \(t=5\) and \(t=6\)

      The average velocity is the rate of change of the position between \(2\) times.

      The average velocity between \(t=5\) and \(t=6\) is \(125\) ft/sec.

      Given that \(y(t)=400t-25t^2\), the average velocity, \(v\)), is the change in position divided by the change in time. \[\begin{aligned} v&=\dfrac{y(6)-y(5)}{6-5} \\ &=[400(6)-25(6)^2]-[400(5)-25(5)^2] \\ &=400(6-5) -25(6+5)(6-5) \\ &=400-275=125 \end{aligned}\] Therefore the average velocity between \(t=5\) and \(t=6\) is \(125\) ft/sec.

      db 

   2. Find the average velocity, \(v\) between \(t=5\) and \(t=5.1\)

      The average velocity between \(t=5\) and \(t=5.1\) is \(147.5\) ft/sec.

      The average velocity between the points \(t=5\) and \(t=5.1\) is: \[\begin{aligned} v&=\dfrac{y(5.1)-y(5)}{5.1-5} \\ &=\dfrac{[400(5.1)-25(5.1)^2]-[400(5)-25(5)^2]}{0.1} \\ &=\dfrac{400(5.1-5)-25(5.1+5)(5.1-5)}{0.1} \\ &=400-25(10.1) =400-252.5=147.5 \end{aligned}\] Therefore the average velocity between \(t=5\) and \(t=5.1\) is \(147.5\) ft/sec.

      db 

   3. Find the average velocity, \(v\) between \(t=5\) and \(t=5.01\)

      The average velocity between \(t=5\) and \(t=5.01\) is \(149.75\) ft/sec.

      The average velocity between the points \(t=5\) and \(t=5.01\) is: \[\begin{aligned} v&=\dfrac{y(5.01)-y(5)}{5.01-5} \\ &=\dfrac{[400(5.01)-25(5.01)^2]-[400(5)-25(5)^2]}{0.01} \\ &=\dfrac{400(5.01-5)-25(5.01+5)(5.01-5)}{0.01} \\ &=400-25(10.01) = 400-250.25 =149.75 \end{aligned}\] Therefore the average velocity between \(t=5\) and \(t=5.01\) is \(149.75\) ft/sec.

      db 

   4. Find the average velocity, \(v\) between \(t=5\) and \(t=5.001\)

      Therefore the average velocity between \(t=5\) and \(t=5.001\) is \(149.975\) ft/sec.

      The average velocity between the points \(t=5\) and \(t=5.001\) is: \[\begin{aligned} v&=\dfrac{y(5.001)-y(5)}{5.001-5} \\ &=\dfrac{[400(5.001)-25(5.001)^2]-[400(5)-25(5)^2]}{0.001} \\ &=\dfrac{400(5.001-5)-25(5.001+5)(5.001-5)}{0.01} \\ &=400-25(10.001) = 400-250.025 =149.975 \end{aligned}\] The average velocity between \(t=5\) and \(t=5.001\) is \(149.975\) ft/sec.

      db 

   5. Find the average velocity, \(v\) between \(t=5\) and \(t=4\)

      The average velocity between \(t=5\) and \(t=4\) is \(175\) ft/sec.

      The average velocity between the points \(t=5\) and \(t=4\) is: \[\begin{aligned} v&=\dfrac{y(5)-y(4)}{5-4} \\ &=[400(5)-25(5)^2]-[400(4)-25(4)^2] \\ &=400(5-4)-25(5+4)(5-4) \\ &=400-225=175 \end{aligned}\] Therefore, the average velocity between \(t=5\) and \(t=4\) is \(175\) ft/sec.

      db 

   6. Find the average velocity, \(v\) between \(t=5\) and \(t=4.9\)

      The average velocity between \(t=5\) and \(t=4.9\) is \(152.5\) ft/sec.

      The average velocity between the points \(t=5\) and \(t=4.9\) is: \[\begin{aligned} v&=\dfrac{y(5)-y(4.9)}{5-4.9} \\ &=\dfrac{[400(5)-25(5)^2]-[400(4.9)-25(4.9)^2])}{0.1} \\ &=\dfrac{400(5-4.9)-25(5+4.9)(5-4.9)}{0.1} \\ &=400-25(9.9) =400-247.5=152.5 \end{aligned}\] Therefore the average velocity between \(t=5\) and \(t=4.9\) is \(152.5\) ft/sec.

      db 

   7. Find the average velocity, \(v\) between \(t=5\) and \(t=4.99\)

      The average velocity between \(t=5\) and \(t=4.99\) is \(150.25\) ft/sec.

      The average velocity between the points \(t=5\) and \(t=4.99\) is: \[\begin{aligned} v&=\dfrac{y(5)-y(4.99)}{5-4.99} \\ &=\dfrac{[400(5)-25(5)^2]-[400(4.99)-25(4.99)^2]}{0.01} \\ &=\dfrac{400(5-4.99)-25(5+4.99)(5-4.99)}{0.01} \\ &=400-25(9.99) =400-249.75=150.25 \end{aligned}\] Therefore the average velocity between \(t=5\) and \(t=4.99\) is \(150.25\) ft/sec.

      db 

   8. Find the average velocity, \(v\) between \(t=5\) and \(t=4.999\)

      Therefore the average velocity between \(t=5\) and \(t=4.999\) is \(150.025\) ft/sec.

      The average velocity between the points \(t=5\) and \(t=4.999\) is: \[\begin{aligned} v&=\dfrac{y(5)-y(4.999)}{5-4.999} \\ &=\dfrac{[400(5)-25(5)^2]-[400(4.999)-25(4.999)^2]}{0.001} \\ &=\dfrac{400(5-4.999)-25(5+4.999)(5-4.999)}{0.001} \\ &=400-25(9.999) =400-249.975=150.025 \end{aligned}\] Therefore the average velocity between \(t=5\) and \(t=4.999\) is \(150.025\) ft/sec.

      db 

   9. Based on the results of the answers above, guess the instantaneous velocity of the projectile at \(t=5\).

      The instantaneous velocity of the projectile at \(t=5\) is \(v_{\text{inst}}=150\) ft/sec.

      The average velocity between \(t=5\) and \(t=6\) is \(125\) ft/sec.
      The average velocity between \(t=5\) and \(t=5.1\) is \(147.5\) ft/sec.
      The average velocity between \(t=5\) and \(t=5.01\) is \(149.75\) ft/sec.
      The average velocity between \(t=5\) and \(t=5.001\) is \(149.975\) ft/sec.

      ---

      The average velocity between \(t=5\) and \(t=4\) is \(175\) ft/sec.
      The average velocity between \(t=5\) and \(t=4.9\) is \(152.5\) ft/sec.
      The average velocity between \(t=5\) and \(t=4.99\) is \(150.25\) ft/sec.
      The average velocity between \(t=5\) and \(t=4.999\) is \(150.025\) ft/sec.

      ---

      We can see that the average velocity approaches \(150\) ft/sec as \(t\) approaches \(5\).
      Therefore, the instantaneous velocity seems to be \(v_{\text{inst}}=150\) ft/sec.

      db 

   10. Finally, use the limit definition to find the instantaneous velocity of the projectile at \(t=5\).

       The instantaneous velocity is the derivative of \(y(t)=400t-25t^2\) at \(t=5\).

       The instantaneous velocity of the projectile at \(t=5\) is \(v_{\text{inst}}=150\,\dfrac{\text{ft}}{\text{sec}}\).

       The instantaneous velocity is the derivative of \(y(t)=400t-25t^2\) at \(t=5\). We use expand and cancel.

       \[\begin{aligned} f'(5)&=\lim_{h\to0} \dfrac{y(5+h)-y(5)}{h} \\ &=\lim_{h\to0} \dfrac{[400(5+h)-25(5+h)^2]-[400(5)-25(5)^2]}{h} \\ &=\lim_{h\to0} \dfrac{400h-25(25+10h+h^2-25)}{h} \\ &=\lim_{h\to0} \dfrac{400h-250h-25h^2}{h} \\ &=\lim_{h\to0} (150-25h)=150 \end{aligned}\] Therefore, the instantaneous velocity at \(t=5\) is \(v_{\text{inst}}=150\,\dfrac{\text{ft}}{\text{sec}}\).

       We check by using the alternate definition of the derivative of \(y(t)=400t-25t^2\) at \(t=5\). We use factor and cancel.

       \[\begin{aligned} f'(5)&=\lim_{t\to 5} \dfrac{y(t)-y(5)}{t-5} \\ &=\lim_{t\to 5} \dfrac{(400t-25t^2)- (400(5)-25(5)^2)}{t-5} \\ &=\lim_{t\to 5} \dfrac{400(t-5) - 25(t+5)(t-5)}{t-5} \\ &=\lim_{t\to 5} [400 - 25(t+5)] \\ &= 400 - 250 = 150 \end{aligned}\] Therefore, the instantaneous velocity at \(t=5\) is \(v_{\text{inst}}=150\,\dfrac{\text{ft}}{\text{sec}}\).

2. The point \(P=(4, 2)\) lies on the curve \(y=\sqrt{x}\). Let \(Q\) be the point \(Q=(x, \sqrt{x})\). Find the slope \(m\) of the secant line \(PQ\) for the following values of \(x\): (Answers should be correct to at least \(4\) places after the decimal point. Feel free to use a calculator.)

   The figure shows the visualization of the secant line to a curve.

   1. Find the slope of \(PQ\) when \(x=5\):

      Remember: \[\begin{aligned} m=\dfrac{y_2 - y_1}{x_2 - x_1} \end{aligned}\]

      The slope of \(PQ\) at \(x=5\) is \(m\approx0.236068\).

      We find the slope, \(m\), between the points \(P=(4, 2)\) and \(Q=(5, \sqrt{5})\): \[\begin{aligned} m&=\dfrac{y(5)-y(4)}{5-4} =\sqrt{5}-2 \\ &\approx2.236068-2=0.236068 \end{aligned}\]

      db 

   2. Find the slope of \(PQ\) when \(x=4.1\):

      The slope (\(m\)) of the secant line PQ is \(m\approx0.248456\).

      We find the slope, \(m\), between the points \(P=(4, 2)\) and \(Q=Q=(4.1, \sqrt{4.1})\): \[\begin{aligned} m&=\dfrac{y(4.1)-y(4)}{4.1-4} =\dfrac{\sqrt{4.1}-2}{4.1-4} \\ &\approx\dfrac{2.0248457-2}{0.1} =0.248457 \end{aligned}\]

      db 

   3. Find the slope of \(PQ\) when \(x=4.01\):

      The slope (\(m\)) of the secant line PQ is \(m\approx0.024984\).

      We find the slope, \(m\), between the points \(P=(4, 2)\) and \(Q=Q=(4.01, \sqrt{4.01})\): \[\begin{aligned} m&=\dfrac{y(4.01)-y(4)}{4.01-4} =\dfrac{\sqrt{4.01}-2}{4.01-4} \\ &\approx\dfrac{2.0024984-2}{0.01} =0.024984 \end{aligned}\]

      db 

   4. Find the slope of \(PQ\) when \(x=4.001\):

      The slope (\(m\)) of the secant line PQ is \(m\approx0.249984\).

      We find the slope, \(m\), between the points \(P=(4, 2)\) and \(Q=Q=(4.001, \sqrt{4.001})\): \[\begin{aligned} m&=\dfrac{y(4.001)-y(4)}{4.001-4} =\dfrac{\sqrt{4.001}-2}{0.001} \\ &\approx\dfrac{2.000249984-2}{0.001} =0.249984 \end{aligned}\]

      db 

   5. Find the slope \(m\) of \(PQ\) when \(x=3\):

      The slope (\(m\)) of the secant line \(PQ\) is \(m\approx0.267949\).

      We find the slope, \(m\), between the points \(P=(4, 2)\) and \(Q=(3, \sqrt{3})\): \[\begin{aligned} m&=\dfrac{y(4)-y(3)}{4-3} =2-\sqrt{3} \\ &\approx2-1.732050808=0.267949 \end{aligned}\]

      db 

   6. Find the slope \(m\) of \(PQ\) when \(x=3.9\):

      The slope (\(m\)) of the secant line PQ is \(m\approx0.251582\).

      We find the slope, \(m\), between the points \(P=(4, 2)\) and \(Q=(3.9, \sqrt{3.9})\): \[\begin{aligned} m&=\dfrac{y(4)-y(3.9)}{4-3.9} =\dfrac{2-\sqrt{3.9}}{4-3.9} \\ &\approx\dfrac{2-1.974841766}{.1} =0.251582 \end{aligned}\]

      db 

   7. Find the slope of \(PQ\) when \(x=3.99\):

      The slope (\(m\)) of the secant line PQ is \(m\approx0.250156\).

      We find the slope, \(m\), between the points \(P=(4, 2)\) and \(Q=(3.99, \sqrt{3.99})\): \[\begin{aligned} m&=\dfrac{y(4)-y(3.99)}{4-3.99} =\dfrac{2-\sqrt{3.99}}{4-3.99} \\ &\approx\dfrac{2-1.997498436}{.01} =0.250156 \end{aligned}\]

      db 

   8. Find the slope of \(PQ\) when \(x=3.999\):

      The slope (\(m\)) of the secant line PQ is \(m\approx0.250016\).

      We find the slope, \(m\), between the points \(P=(4, 2)\) and \(Q=(3.999, \sqrt{3.999})\): \[\begin{aligned} m&=\dfrac{y(4)-y(3.999)}{4-3.999} =\dfrac{2-\sqrt{3.999}}{4-3.999} \\ &\approx\dfrac{2-1.999749984}{.001} =0.250016 \end{aligned}\]

      db 

   9. Based on the results of the answers above, guess the slope of the tangent line at \(P\) where \(x=4\).

      The slope of tangent line at \(P\) where \(x=4\) is \(m=\dfrac{1}{4}=0.25\).

      The slope between the points \(P=(4, 2)\) and \(Q=(5, \sqrt{5})\) is \(m\approx0.236068\).
      The slope between the points \(P=(4, 2)\) and \(Q=(4.1, \sqrt{4.1})\) is \(m\approx0.248456\).
      The slope between the points \(P=(4, 2)\) and \(Q=(4.01, \sqrt{4.01})\) is \(m\approx0.024984\).
      The slope between the points \(P=(4, 2)\) and \(Q=(4.001, \sqrt{4.001})\) is \(m\approx0.249984\).

      ---

      The slope between the points \(P=(4, 2)\) and \(Q=(3, \sqrt{3})\) is \(m\approx0.267949\).
      The slope between the points \(P=(4, 2)\) and \(Q=(3.9, \sqrt{3.9})\) is \(m\approx0.251582\).
      The slope between the points \(P=(4, 2)\) and \(Q=(3.99, \sqrt{3.99})\) is \(m\approx0.250156\).
      The slope between the points \(P=(4, 2)\) and \(Q=(3.999, \sqrt{3.999})\) is \(m\approx0.250016\).

      ---

      We can see that the slope (\(m\)) of line \(PQ\) approaches \(m=0.25\) as \(Q\) approaches \(P=(4,2)\). Therefore, we guess the slope of tangent line at \(P\) where \(x=4\) is \(m=0.25\).

      db 

   10. Finally use the limit definition to find the slope of the tangent line at \(P\) where \(x=4\).

       To do the limit, multiply by a conjugate.

       The slope of tangent line at \(P\) where \(x=4\) is \(m=\dfrac{1}{4}=0.25\).

       We take the derivative at the point \(x=4\) of the function \(y(x)=\sqrt{x}\). We take the limit by multiplying by a conjugate: \[\begin{aligned} f'(4)&=\lim_{h\to0} \dfrac{y(4+h)-y(4)}{h} \\ &=\lim_{h\to0} \dfrac{\sqrt{4+h}-2}{h} \\ &=\lim_{h\to0} \dfrac{\sqrt{4+h}-2}{h}\cdot \dfrac{\sqrt{4+h}+2}{\sqrt{4+h}+2} \\ &=\lim_{h\to0} \dfrac{4+h-4}{h(\sqrt{4+h}+2)} \\ &=\lim_{h\to0} \dfrac{1}{\sqrt{4+h}+2}=\dfrac{1}{4} \\ \end{aligned}\] Therefore, the slope of tangent line at \(x=4\) is \(m=\dfrac{1}{4}=0.25\)

       We check by using the alternate definition to find the derivative of the function \(y(x)=\sqrt{x}\) at the point \(x=4\). We take the limit by multiplying by a conjugate: \[\begin{aligned} f'(4)&=\lim_{x\to 4} \dfrac{y(x)-y(4)}{x-4} \\ &=\lim_{x\to 4} \dfrac{\sqrt{x}-\sqrt{4}}{x-4} \\ &=\lim_{x\to 4} \dfrac{\sqrt{x}-\sqrt{4}}{x-4}\cdot \dfrac{\sqrt{x}+\sqrt{4}}{\sqrt{x}+\sqrt{4}} \\ &=\lim_{x\to 4} \dfrac{(x-4)}{(x-4)(\sqrt{x}+\sqrt{4})} \\ &=\lim_{x\to 4} \dfrac{1}{\sqrt{x}+\sqrt{4}} =\dfrac{1}{2\sqrt{4}} \end{aligned}\] Therefore, the slope of tangent line at \(x=4\) is \(m=\dfrac{1}{4}=0.25\)

---

Find the derivative of each function at the indicated point by computing the appropriate limit.

3. \(f(x)=x^3\) at \(a=2\).

   There are \(2\) formulas for computing the derivative of the function \(f(x)\) at the point \(x=a\): \[ f'(a)=\lim_{h\to0} \dfrac{f(a+h)-f(a)}{h} \] \[ f'(a)=\lim_{x\to a} \dfrac{f(x)-f(a)}{x-a} \] Use whichever formula is convenient.

   Also remember: \[ (a+h)^3=a^3+3a^2h+3ah^2+h^3 \]

   \(f'(2)=12\)

   Solve for the limit by using the first method. In this case, \(f(x)=x^3\) and \(a=2\). \[\begin{aligned} f'(2)&=\lim_{h\to0} \dfrac{f(2+h)-f(2)}{h} \\ &=\lim_{h\to0} \dfrac{(2+h)^3 - 8}{h} \\ &=\lim_{h\to0} \dfrac{12h + 6h^2 + h^3}{h} \\ &=\lim_{h\to0} (12+6h + h^2) = 12 \end{aligned}\]

   You can also solve using the second method, with \(f(x)=x^3\) and \(a=2\). \[\begin{aligned} f'(2)&=\lim_{x\to2} \dfrac{f(x) - f(2)}{x-2} \\ &=\lim_{x\to2} \dfrac{x^3 - 8}{x-2} \\ &=\lim_{x\to2} \dfrac{(x-2)(x^2 + 2x + 4)}{x-2} \\ &=\lim_{x\to2} (x^2 + 2x + 4) = 12 \end{aligned}\]

   db 

   Does it matter which formula we use for the derivative? No! We can use whichever formula seems easier. Of course, we can't know which will be easier until we do them, so we just pick one.




4. \(g(y)=\sqrt{y}\) at \(a=9\).

   There are 2 formulas for computing the derivative of the function \(g(y)\) at the point \(y=a\): \[ g'(a)=\lim_{g\to0} \dfrac{g(a+h)-g(a)}{h} \] \[ g'(a)=\lim_{y\to a} \dfrac{g(y)-g(a)}{y-a} \] Use whichever formula is convenient.

   \(g'(9)=\dfrac{1}{6}\)

   \(g(y)=\sqrt{y}\) and \(a=9\). \[\begin{aligned} g'(9)&=\lim_{h\to0} \dfrac{g(9+h)-g(9)}{h} \\ &=\lim_{h\to0} \dfrac{\sqrt{9+h} -3}{h} \\ &=\lim_{h\to0} \dfrac{\sqrt{9+h} -3}{h} \,\dfrac{\sqrt{9+h} +3}{\sqrt{9+h} +3} \\ &=\lim_{h\to0} \dfrac{9+h-9}{h(\sqrt{9+h} +3)} \\ &=\lim_{h\to0} \dfrac{1}{\sqrt{9+h} +3} =\dfrac{1}{6} \end{aligned}\]

   \(g(y)=\sqrt{y}\) and \(a=9\). \[\begin{aligned} g'(9)&=\lim_{y\to9} \dfrac{g(y) - g(9)}{y-9} \\ &=\lim_{y\to9} \dfrac{\sqrt{y} -3}{y-9} \\ &=\lim_{y\to9} \dfrac{\sqrt{y} -3}{y-9} \dfrac{\sqrt{y}+3}{\sqrt{y}+3} \\ &=\lim_{y\to9} \dfrac{(y-9)}{(y-9)(\sqrt{y}+3)} \\ &=\lim_{y\to9} \dfrac{1}{\sqrt{y}+3} =\dfrac{1}{6} \end{aligned}\]

   db 

5. \(j(k)=\dfrac{1}{\sqrt{k}}\) at \(a=4\).

   First put the limit over a common denominator. Then, multiply the numerator and denominator by a conjugate.

   \(j'(4)=-\,\dfrac{1}{16}\)

   We use method \(1\) to compute the derivative. We check using method \(2\).

   We first write out the definition and put the terms over a common denominator: \[\begin{aligned} j'(9)&=\lim_{h\to0} \dfrac{j(4+h)-j(4)}{h} \\ &=\lim_{h\to0} \dfrac{\dfrac{1}{\sqrt{4+h}} -\dfrac{1}{2}}{h} \\ &=\lim_{h\to0} \dfrac{1}{h}\,\dfrac{(2-\sqrt{4+h})}{2\sqrt{4+h}} \end{aligned}\] Now we multiply and divide by the conjugate: \[\begin{aligned} j'(9)&=\lim_{h\to0} \dfrac{1}{h}\dfrac{(2-\sqrt{4+h})}{2\sqrt{4+h}} \dfrac{(2+\sqrt{4+h})}{(2+\sqrt{4+h})} \\ &=\lim_{h\to0} \dfrac{4-(4+h)}{2h\sqrt{4+h}(2+\sqrt{4+h})} \\ &=\lim_{h\to0} \dfrac{-1}{2\sqrt{4+h}(2+\sqrt{4+h})} \\ &=-\,\dfrac{1}{2\sqrt{4}(2+\sqrt{4})} =-\,\dfrac{1}{16} \end{aligned}\]

   db 

   We check using method 2.

   We first write out the definition and put the terms over a common denominator: \[\begin{aligned} j'(4)&=\lim_{k\to4} \dfrac{j(k) - j(4)}{x-4} \\ &=\lim_{k\to4} \dfrac{\dfrac{1}{\sqrt{k}} -\,\dfrac{1}{2}}{k-4} \\ &=\lim_{k\to4} \dfrac{1}{k-4}\dfrac{(2-\sqrt{k})}{2\sqrt{k}} \\ \end{aligned}\] Now we multiply and divide by the conjugate: \[\begin{aligned} &=\lim_{k\to4} \dfrac{1}{k-4}\dfrac{(2-\sqrt{k})}{2\sqrt{k}} \dfrac{2+\sqrt{k}}{(2+\sqrt{k})} \\ &=\lim_{k\to4} \dfrac{1}{k-4}\dfrac{4-k}{2\sqrt{k}(2+\sqrt{k})} \\ &=\lim_{k\to4} -\,\dfrac{1}{2\sqrt{k}(2+\sqrt{k})} \\ &=-\,\dfrac{1}{2\sqrt{4}(2+\sqrt{4})} =-\,\dfrac{1}{16} \end{aligned}\]

6. \(k(b)=b^4\) at \(a=-2\).

   There are 2 formulas for computing the derivative of the function \(k(b)\) at the point \(b=a\): \[ f'(a)=\lim_{h\to0} \dfrac{k(a+h)-k(a)}{h} \] \[ k'(a)=\lim_{b\to a} \dfrac{k(b)-k(a)}{b-a} \] Use whichever formula is convenient. Also, remeber the formula for the Difference of Squares: \(a^2-b^2=(a+b)(a-b)\)

   \(k'(-2)=-32\)

   We use method \(1\) to compute the derivative. We check using method \(2\).

   We use a combination of factoring followed by expanding and then cancel.

   \[\begin{aligned} k'(-2)&=\lim_{h\to0} \dfrac{k(-2+h)-k(-2)}{h} \\ &=\lim_{h\to0} \dfrac{(-2+h)^4-16}{h} \\ &=\lim_{h\to0} \dfrac{[(-2+h)^2+4][(-2+h)^2-4]}{h} \\ &=\lim_{h\to0} \dfrac{(4-4h+h^2+4)(4-4h+h^2-4)}{h} \\ &=\lim_{h\to0} \dfrac{(8-4h+h^2)(-4h+h^2)}{h} \\ &=\lim_{h\to0} (8-4h+h^2)(-4+h) =-32 \end{aligned}\]

   db 

   We check using method \(2\).

   \[\begin{aligned} k'(b)&=\lim_{b\to -2} \dfrac{k(b)-k(-2)}{b+2} \\ &=\lim_{b\to -2} \dfrac{b^4-16}{b+2} \\ &=\lim_{b\to -2} \dfrac{(b^2+4)(b^2-4)}{b+2} \\ &=\lim_{b\to -2} \dfrac{(b^2+4)(b+2)(b-2)}{b+2} \\ &=\lim_{b\to -2} (b^2+4)(b-2) \\ &= (8)(-4) = -32 \end{aligned}\]

---

7. Find the derivative of \(g(x)=3x^2\) at the points listed below:

   1. \(a=4\).

      There are 2 formulas for computing the derivative of the function \(f(x)\) at the point \(x=a\): \[ f'(a)=\lim_{h\to0} \dfrac{g(a+h)-g(a)}{h} \] \[ f'(a)=\lim_{x\to a} \dfrac{g(x)-fg(a)}{x-a} \] Use whichever formula is convenient.

      \(g'(4)=24\)

      Solve for the limit by using the first method, with \(g(x)=3x^2\) and \(a=4\). \[\begin{aligned} g'(4)&=\lim_{h\to0} \dfrac{3(4+h)^2 - 48}{h} \\ &=\lim_{h\to0} \dfrac{24h + 3h^2}{h} \\ &=\lim_{h\to0} (24 + 3h) = 24 \end{aligned}\]

      You can also solve using the second method, with \(g(x)=3x^2\) and \(a=4\). \[\begin{aligned} g'(4)&=\lim_{x\to4} \dfrac{3x^2 - 48}{x-4} \\ &=\lim_{x\to4} \dfrac{3(x+4)(x-4)}{x-4} \\ &=\lim_{x\to4} 3(x+4) = 24 \end{aligned}\]

      db 

   2. \(a=7\).

      \(g'(7)=42\)

      Solve for the limit by using the first method, with \(g(x)=3x^2\) and \(a=7\). \[\begin{aligned} g'(7)&=\lim_{h\to0} \dfrac{3(7+h)^2 - 147}{h} \\ &=\lim_{h\to0} \dfrac{42h+3h^2}{h} \\ &=\lim_{h\to0} (42+3h) = 42 \end{aligned}\]

      You can also solve using the second method, with \(f(x)=3x^2\) and \(a=7\). \[\begin{aligned} g'(7)&=\lim_{x\to7} \dfrac{3x^2 - 147}{x-7} \\ &=\lim_{x\to7} \dfrac{3(x+7)(x-7)}{x-7} \\ &=\lim_{x\to7} 3(x+7) \\ &=\lim_{x\to7} (3x + 21) = 42 \end{aligned}\]

      db 

8. Find the derivative of the functions below at the point \(a=10\).

   1. \(w(z)=4z^2\).

      There are 2 formulas for computing the derivative of the function \(w(z)\) at the point \(z=a\): \[ w'(a)=\lim_{h\to0} \dfrac{w(a+h)-w(a)}{h} \] \[ w'(a)=\lim_{z\to a} \dfrac{w(z)-w(a)}{z-a} \] Use whichever formula is convenient.

      \(w'(10)=80\)

      We solve for the limit by using the first method, with \(w(z)=4z^2\) and \(a=10\). \[\begin{aligned} w'(10)&=\lim_{h\to0} \dfrac{4(10+h)^2 - 400}{h} \\ &=\lim_{h\to0} \dfrac{80h+4h^2}{h} \\ &=\lim_{h\to0} (80+4h) = 80 \end{aligned}\]

      We can also solve using the second method, with \(w(z)=4z^2\) and \(a=10\). \[\begin{aligned} w'(10)&=\lim_{z\to10} \dfrac{4z^2 - 400}{z-10} \\ &=\lim_{z\to10} \dfrac{4(z+10)(z-10)}{z-10} \\ &=\lim_{z\to10} (4z + 40) = 80 \end{aligned}\]

      db 

   2. \(p(t)=3t^3\).

      Remember: \[\begin{aligned} (a+h)^3&=a^3+3a^2h+3ah^2+h^3 \\ a^3-b^3&=(a-b)(a^2+ab+b^2) \end{aligned}\]

      \(p'(10)=900\)

      We solve for the limit by using the first method, with \(p(t)=3t^3\) and \(t=10\). \[\begin{aligned} p'(10)&=\lim_{h\to0} \dfrac{3(10+h)^3 - 3000}{h} \\ &=\lim_{h\to0} \dfrac{900h + 90h^2+3h^3}{h} \\ &=\lim_{h\to0} (900+90h+3h^2) = 900 \end{aligned}\]

      We can also solve using the second method, with \(p(t)=3t^3\) and \(a=10\). \[\begin{aligned} p'(10)&=\lim_{t\to10} \dfrac{3t^3 - 3000}{t-10} \\ &=\lim_{t\to10} \dfrac{3(t-10)(t^2 + 10t + 100)}{t-10} \\ &=\lim_{t\to10} 3(t^2 + 10t + 100) = 900 \end{aligned}\]

      db 

9. Find the slope of the tangent line to the function, \(z(y)=3y^2-2y^3\), at \(y=2\).

   The slope of the tangent line to a function, \(z(y)\), at a point \(y=a\) is the derivative of the function at \(y=a\), that is \(m=z'(a)\).

   The slope at \(y=2\) is \(m=-12\).

   \[\begin{aligned} m&=z'(2)=\lim_{h\to 0} \dfrac{z(2+h)-z(2)}{h} \\ &=\lim_{h\to 0} \dfrac{[3(2+h)^2-2(2+h)^3]-[3\cdot2^2-2(2^3)]}{h} \\ &=\lim_{h\to 0} \dfrac{1}{h}\Big([3(4+4h+h^2) \\ &\qquad\qquad-2(8+12h+6h^2+h^3)]-[12-16]\Big) \\ &=\lim_{h\to 0} \dfrac{1}{h}\Big(12+12h+3h^2 \\ &\qquad\qquad-16-24h-12h^2-2h^3+4\Big) \\ &=\lim_{h\to 0} \dfrac{-12h-9h^2-2h^3}{h} \\ &=\lim_{h\to 0} (-12-9h-2h^2)=-12 \\ \end{aligned}\]

   db 

b. Tangent Lines

1

10. Compute the tangent line to \(y=\sqrt{x}\) at \(x=4\). Then find its \(y\)-intercept.

    The figure shows the tangent line to the curve.

    

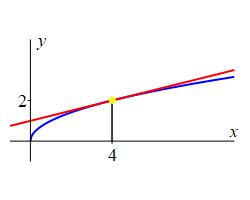
    Evaluate the function and find its derivative at \(x=4\). Then use the formula: \[ f_{\tan}(x)=f(4)+f'(4)(x-4) \]

    \(y=\dfrac{1}{4}x+1\)
    The \(y\)-intercept is \(b=1\).

    We identify \(f(x)=\sqrt{x}\) and \(a=4\). Then: \[ f(4)=2 \] In a previous problem we found \[ f'(4)=\dfrac{1}{4} \] So the equation of the tangent line is: \[\begin{aligned} y&=f(a)+f'(a)(x-a) \\ &=f(4)+f'(4)(x-4) \\ &=2+\dfrac{1}{4}(x-4) \\ &=\dfrac{1}{4}x+1 \end{aligned}\] We identify the \(y\)-intercept as \(b=1\).

    db 

11. Compute the tangent line to \(y=x\sqrt{x}\) at \(x=3\). Then find its \(x\)-intercept.

    Evaluate the function and find its derivative at \(x=3\). Then use the formula: \[ f_{\tan}(x)=f(3)+f'(3)(x-3) \]

    The tangent line is \(y=\dfrac{3\sqrt{3}}{2}x-\dfrac{3\sqrt{3}}{2}\).
    The \(x\)-intercept is \(x=1\).

    We identify \(f(x)=x\sqrt{x}\) and \(x=a=3\). Then: \[ f(3)=3\sqrt{3} \] To compute the slope, we find the appropriate limit by multiplying by the conjugate: \[\begin{aligned} f'(3)&=\lim_{h\to0} \dfrac{f(3+h)-f(3)}{h} \\ &=\lim_{h\to0} \dfrac{(3+h)\sqrt{3+h}-3\sqrt{3}}{h} \\ &=\lim_{h\to0} \dfrac{((3+h)\sqrt{3+h}-3\sqrt{3})}{h} \,\dfrac{[(3+h)\sqrt{3+h}+3\sqrt{3}]}{[(3+h)\sqrt{3+h}+3\sqrt{3}]} \\ &=\lim_{h\to0} \dfrac{(3+h)^3-(3)^3}{h[(3+h)\sqrt{3+h}+3\sqrt{3}]} \\ &=\lim_{h\to0} \dfrac{27+27h+9h^2+h^3-27}{h[(3+h)\sqrt{3+h}+3\sqrt{3}]} \\ &=\lim_{h\to0} \dfrac{(27+9h+h^2)}{(3+h)\sqrt{3+h}+3\sqrt{3}} \\ &=\dfrac{27}{6\sqrt{3}} =\dfrac{3\sqrt{3}}{2} \end{aligned}\] So the equation of the tangent line is: \[\begin{aligned} y&=f(3)+f'(3)(x-3) \\ &=3\sqrt{3}+\dfrac{3\sqrt{3}}{2}(x-3) \\ &=\dfrac{3\sqrt{3}}{2}x-\dfrac{3\sqrt{3}}{2} \end{aligned}\] After that, we set \(y=0\) to find the \(x\)-intercept. \[\begin{aligned} \dfrac{3\sqrt{3}}{2}x-\dfrac{3\sqrt{3}}{2}&=0 \\ \dfrac{3\sqrt{3}}{2}(x-1)=0 \\ x=1 \end{aligned}\] We identify the \(x\)-intercept as \(x=1\).

    db 

12. Find the tangent line to \(y=x^2\) at the following points. Also find the \(y\)-intercept of each tangent line.

    1. \(x=3\)

       Evaluate the function and find its derivative at \(x=3\). Then use the formula: \[ f_{\tan}(x)=f(3)+f'(3)(x-3) \]

       The equation of the tangent line is \(y=6x-9\).
       The \(y\)-intercept is \(y=-9\).

       We identify \(f(x)=x^2\) and \(x=a=3\). Then: \(f(3)=9\). We compute the slope: \[\begin{aligned} f'(3)&=\lim_{h\to0} \dfrac{f(3+h)-f(3)}{h} \\ &=\lim_{h\to0} \dfrac{(3+h)^2-9}{h} \\ &=\lim_{h\to0} \dfrac{9+6h+h^2-9}{h} \\ &=\lim_{h\to0} (6+h) =6 \end{aligned}\] So, the equation of the tangent line is: \[\begin{aligned} y&=f(3)+f'(3)(x-3) \\ &=9+6(x-3) \\ &=9+6x-18 =6x-9 \end{aligned}\] So the \(y\)-intercept is \(y=-9\).

       db 

    2. \(x=6\)

       The equation of the tangent line is \(y=12x-36\).
       The \(y\)-intercept is \(y=-36\).

       We identify \(f(x)=x^2\) and \(x=a=6\). Then: \(f(6)=36\) We compute the slope: \[\begin{aligned} f'(6)&=\lim_{h\to0} \dfrac{f(6+h)-f(6)}{h} \\ &=\lim_{h\to0} \dfrac{(6+h)^2-36}{h} \\ &=\lim_{h\to0} \dfrac{36+12h+h^2-36}{h} \\ &=\lim_{h\to0} (12+h) =12 \end{aligned}\] So, the equation of the tangent line is: \[\begin{aligned} y&=f(6)+f'(6)(x-6) \\ &=36+12(x-6) \\ &=36+12x-72 =12x-36 \end{aligned}\] and the \(y\)-intercept is \(y=-36\).

       db 

    3. \(x=a\)

       The equation of the tangent line is \(y==2ax-a^2\).
       The \(y\)-intercept is \(y=-a^2\).

       We identify \(f(x)=x^2\) and \(x=a\). Then: \(f(a)=a^2\) We compute the slope: \[\begin{aligned} f'(a)&=\lim_{h\to0} \dfrac{f(a+h)-f(a)}{h} \\ &=\lim_{h\to0} \dfrac{(a+h)^2-a^2}{h} \\ &=\lim_{h\to0} \dfrac{a^2+2ah+h^2-a^2}{h} \\ &=\lim_{h\to0} (2a+h) =2a \end{aligned}\] So, the equation of the tangent line is: \[\begin{aligned} y&=f(a)+f'(a)(x-a) \\ &=a^2+2a(x-a) \\ &=2ax-a^2 \end{aligned}\] and the \(y\)-intercept is \(y=-a^2\).

       We check our general result, \(y=2ax-a^2\), against the two particular cases:

       For \(x=3\), the tangent line is \(y=6x-9\).

       For \(x=6\), the tangent line is \(y=12x-36\).

13. Find the tangent line to \(y=x^3\) at the following points. Also find the \(y\)-intercept of each tangent line.

    1. \(x=2\)

       Evaluate the function and find its derivative at \(x=2\). Then use the formula: \[ f_{\tan}(x)=f(2)+f'(2)(x-2) \]

       The tangent line is \(y=8+12(x-2)=12x-16\).
       The \(y\)-intercept is \(y=-16\).

       We identify \(f(x)=x^3\) and \(x=a=2\). Then: \[ f(2)=2^3=8 \] We compute the slope: \[\begin{aligned} f'(2)&=\lim_{h\to0} \dfrac{f(2+h)-f(2)}{h} \\ &=\lim_{h\to0} \dfrac{(2+h)^3-8}{h} \\ &=\lim_{h\to0} \dfrac{(8+12h+6h^2+h^3)-8}{h} \\ &=\lim_{h\to0} (12+6h+h^2) =12 \end{aligned}\] So the equation of the tangent line is: \[\begin{aligned} y&=f(2)+f'(2)(x-2) \\ &=8+12(x-2) =12x -16 \end{aligned}\] So the \(y\)-intercept is \(b=-16\).

       db 

    2. \(x=3\)

       The equation of the tangent line is \(y=27+27(x-3)=27x-54\).
       The \(y\)-intercept is \(y=-54\).

       We identify \(f(x)=x^3\) and \(x=a=3\). Then: \[ f(3)=3^3=27 \] We compute the slope: \[\begin{aligned} f'(3)&=\lim_{h\to0} \dfrac{f(3+h)-f(3)}{h} \\ &=\lim_{h\to0} \dfrac{(3+h)^3-27}{h} \\ &=\lim_{h\to0} \dfrac{(27+27h+9h^2+h^3)-27}{h} \\ &=\lim_{h\to0} (27+9h+h^2) =27 \end{aligned}\] So the equation of the tangent line is: \[\begin{aligned} y&=f(3)+f'(3)(x-3) \\ &=27+27(x-3) =27x-54 \end{aligned}\] So the \(y\)-intercept is \(y=-54\).

       db 

    3. \(x=p\)

       The equation of the tangent line is \(y=p^3+3p^2(x-p)=3p^2x-2p^3\).
       The \(y\)-intercept is \(y=-2p^3\).

       We identify \(f(x)=p^3\) and \(x=p\). Then: \[ f(p)=p^3 \] We compute the slope: \[\begin{aligned} f'(p)&=\lim_{h\to0} \dfrac{f(p+h)-f(p)}{h} \\ &=\lim_{h\to0} \dfrac{(p+h)^3-p^3}{h} \\ &=\lim_{h\to0} \dfrac{(p^3+3p^2h+3ph^2+h^3)-p^3}{h} \\ &=\lim_{h\to0} (3p^2+3ph+h^2) =3p^2 \end{aligned}\] So the equation of the tangent line is: \[\begin{aligned} y&=f(p)+f'(p)(x-p) \\ &=p^3+3p^2(x-p) =3p^2x-2p^3 \end{aligned}\] So the \(y\)-intercept is \(y=-2p^3\).

       We check our general result, \(y=3p^2x-2p^3\), against the two particular cases:

       For \(x=2\), the tangent line is \(y=12x-16\).

       For \(x=3\), the tangent line is \(y=27x-54\).

14. Find the tangent line to \(y=-\sqrt{x}\) at \(x=4\) and its \(y\)-intercept.

    Evaluate the function and find its derivative at \(x=4\). Then use the formula: \[ f_{\tan}(x)=f(4)+f'(4)(x-4) \]

    The tangent line is \(y=-\,\dfrac{1}{4}x - 1\).
    The \(y\)-intercept is \(y=-1\).

    We identify \(f(x)=-\sqrt{x}\) and \(x=a=4\). Then: \[ f(4)=-\sqrt{4}=-2 \] We compute the slope: \[\begin{aligned} f'(4)&=\lim_{h\to0} \dfrac{f(4+h)-f(4)}{h} \\ &=\lim_{h\to0} \dfrac{-\sqrt{4+h}+2}{h} \\ &=\lim_{h\to0} \dfrac{-\sqrt{4+h}+2}{h}\cdot \dfrac{\sqrt{4+h}+2}{\sqrt{4+h}+2} \\ &=\lim_{h\to0} \dfrac{4-(4+h)}{h(\sqrt{4+h}+2)} \\ &=\lim_{h\to0} \dfrac{-1}{\sqrt{4+h}+2} =-\,\dfrac{1}{4} \end{aligned}\] So the equation of the tangent line is: \[\begin{aligned} y&=f(4)+f'(4)(x-4) \\ &=-2-\dfrac{1}{4}(x-4) =-\,\dfrac{1}{4}x - 1 \end{aligned}\] So the \(y\)-intercept is \(y=-1\).

    db 

c. Derivative as a Function

1

2

3

Every question in this section will be solved using Method 1, and checked using Method 2. You can use either one.

15. Consider the \(g(x)=3x^2\):

    1. Find the derivative \(g'(x)\) as a function of \(x\).

       The derivative of the function \(f(x)\) is the function \(f'(x)\) given by either of the limits: \[\begin{aligned} f'(x)&=\lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} \\ &=\lim_{z\to x} \dfrac{f(z)-f(x)}{z-x} \end{aligned}\] Use whichever formula is convenient. Try both.
       Remember \(h\) or \(z\) is the variable. \(x\) is a constant!

       \(g'(x)=6x\)

       We find the derivative by using the first method, with \(g(x)=3x^2\). \[\begin{aligned} g'(x)&=\lim_{h\to0} \dfrac{3(x+h)^2 - 3x^2}{h} \\ &=\lim_{h\to0} \dfrac{3(x^2+2xh+h^2)-3x^2}{h} \\ &=\lim_{h\to0} (6x + 3h) = 6x \end{aligned}\]

       db 

       We can also solve using the second method, with \(f(x)=3x^2\). \[\begin{aligned} g'(x)&=\lim_{z\to x} \dfrac{3z^2 - 3x^2}{z-x} \\ &=\lim_{z\to x} \dfrac{3(z+x)(z-x)}{z-x} \\ &=\lim_{z\to x} 3(z+x) = 6x \end{aligned}\]

    2. Use the derivative to find \(g'(4)\).

       Just plug a number into \(g'(x)\).

       \(g'(4)=24\)

       We simply plug \(x=4\) into \(g'(x)=6x\): \[\begin{aligned} g'(4)=24 \end{aligned}\]

       db 

    3. Use the derivative to find \(g'(7)\).

       \(g'(7)=42\)

       We simply plug \(x=7\) into \(g'(x)=6x\): \[\begin{aligned} g'(7)=42 \end{aligned}\]

       db 

       Compare this exercise to a previous exercise. Notice how much easier it is to take a derivative as a function, and then plug in numbers, rather than taking the derivatives separately at each point.

16. Consider the function \(f(x)=\sqrt{x}\).

    The figure shows the tangent line to the curve at various points.

    

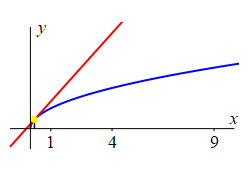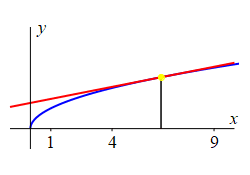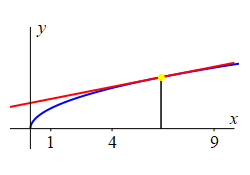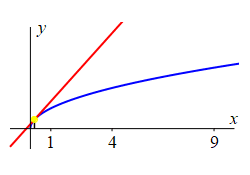
    1. Find the derivative \(f'(x)\) as a function of \(x\).

       The derivative of the function \(f(x)\) is the function \(f'(x)\) given by either of the limits: \[\begin{aligned} f'(x)&=\lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} \\ &=\lim_{z\to x} \dfrac{f(z)-f(x)}{z-x} \end{aligned}\] Use whichever formula is convenient. Try both.

       \(f'(x)=\dfrac{1}{2\sqrt{x}}\)

       To do the limit, we multiply by the conjugate: \[\begin{aligned} f'(x)&=\lim_{h\to0} \dfrac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to0} \dfrac{\sqrt{x+h}-\sqrt{x}}{h} \\ &=\lim_{h\to0} \dfrac{\sqrt{x+h}-\sqrt{x}}{h}\cdot \dfrac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}} \\ &=\lim_{h\to0} \dfrac{(x+h)-x}{h(\sqrt{x+h}+\sqrt{x})} \\ &=\lim_{h\to0} \dfrac{1}{\sqrt{x+h}+\sqrt{x}} =\dfrac{1}{2\sqrt{x}} \end{aligned}\]

       We can also solve using the second method. To do the limit, we multiply by the conjugate: \[\begin{aligned} \dfrac{df}{dx}&=\lim_{z\to x} \dfrac{f(z)-f(x)}{z-x} \\ &=\lim_{z\to x} \dfrac{\sqrt{z}-\sqrt{x}}{z-x} \\ &=\lim_{z\to x} \dfrac{\sqrt{z}-\sqrt{x}}{z-x}\cdot \dfrac{\sqrt{z}+\sqrt{x}}{\sqrt{z}+\sqrt{x}} \\ &=\lim_{z\to x} \dfrac{(z-x)}{(z-x)(\sqrt{z}+\sqrt{x})} \\ &=\lim_{z\to x} \dfrac{1}{\sqrt{z}+\sqrt{x}} =\dfrac{1}{2\sqrt{x}} \end{aligned}\]

    2. Use the derivative to find \(f'(1)\).

       Just plug a number into \(f'(x)\).

       \(f'(1)=\dfrac{1}{2}\)

       We simply plug \(x=1\) into \(f'(x)=\dfrac{1}{2\sqrt{x}}\): \[ f'(1)=\dfrac{1}{2} \]

    3. Find the tangent line to \(y=f(x)\) at \(x=1\).

       The tangent line is \(y=f(1)+f'(1)(x-1)\).

       \(y=\dfrac{1}{2}x+\dfrac{1}{2}\)

       Since \(f(1)=\sqrt{1}=1\) and \(f'(1)=\dfrac{1}{2}, the tangent line is: \[\begin{aligned} y&=f(1)+f'(1)(x-1) \\ &=1+\dfrac{1}{2}(x-1) =\dfrac{1}{2}x+\dfrac{1}{2} \end{aligned}\]

    4. Use the derivative to find \(f'(4)\).

       \(f'(4)=\dfrac{1}{4}\)

       We simply plug \(x=4\) into \(f'(x)=\dfrac{1}{2\sqrt{x}}\): \[ f'(4)=\dfrac{1}{4} \]

       Compare this exercise to a previous exercise. Notice how much easier it is to take a derivative as a function, and then plug in numbers, rather than taking the derivatives separately at each point.

    5. Find the tangent line to \(y=f(x)\) at \(x=4\).

       \(y=\dfrac{1}{4}x+1\)

       Since \(f(4)=\sqrt{4}=2\) and \(f'(4)=\dfrac{1}{4}\), the tangent line is: \[\begin{aligned} y&=f(4)+f'(4)(x-4) \\ &=2+\dfrac{1}{4}(x-4) =\dfrac{1}{4}x+1 \end{aligned}\]

    6. Use the derivative to find \(f'(9)\).

       \(f'(9)=\dfrac{1}{6}\)

       We simply plug \(x=9\) into \(f'(x)=\dfrac{1}{2\sqrt{x}}\): \[ f'(9)=\dfrac{1}{6} \]

       Compare this exercise to a previous exercise. Again, notice how much easier it is to take a derivative as a function, and then plug in numbers, rather than taking the derivatives separately at each point.

    7. Find the tangent line to \(y=f(x)\) at \(x=9\).

       \(y=\dfrac{1}{6}x+\dfrac{3}{2}\)

       Since \(f(9)=\sqrt{9}=3\) and \(f'(9)=\dfrac{1}{6}\), the tangent line is: \[\begin{aligned} y&=f(9)+f'(9)(x-9) \\ &=3+\dfrac{1}{6}(x-9) =\dfrac{1}{6}x+\dfrac{3}{2} \end{aligned}\]

    8. Use the derivative to find \(f'(a)\) at a general point \(x=a\).

       \(f'(a)=\dfrac{1}{2\sqrt{a}}\)

       We simply plug \(x=a\) into \(f'(x)=\dfrac{1}{2\sqrt{x}}\): \[\begin{aligned} f'(a)=\dfrac{1}{2\sqrt{a}} \end{aligned}\]

    9. Find the tangent line to \(y=g(x)\) at a general point \(x=a\).

       \(y=\dfrac{1}{2\sqrt{a}}x+\dfrac{\sqrt{a}}{2}\)

       Since \(f(a)=\sqrt{a}\) and \(f'(a)=\dfrac{1}{2\sqrt{a}}\), the tangent line is: \[\begin{aligned} y&=f(9)+f'(9)(x-9) \\ &=\sqrt{a}+\dfrac{1}{2\sqrt{a}}(x-a) =\dfrac{1}{2\sqrt{a}}x+\dfrac{\sqrt{a}}{2} \end{aligned}\]

       By finding the tangent line at a general point, you don't need to repeat the evaluation of the derivative and the computation of the tangent line. Just plug in a value of \(a\).

17. Consider the function \(g(x)=\dfrac{1}{x}\).

    1. Find the derivative \(g'(x)\) as a function of \(x\).

       The derivative of the function \(f(x)\) is the function \(f'(x)\) given by either of the limits: \[\begin{aligned} f'(x)&=\lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} \\ &=\lim_{z\to x} \dfrac{f(z)-f(x)}{z-x} \end{aligned}\] Use whichever formula is convenient. Try both.

       \(g'(x)=-\,\dfrac{1}{x^2}\)

       To do the limit, we put the terms over a common denominator: \[\begin{aligned} g'(x)&=\lim_{h\to0} \dfrac{g(x+h)-g(x)}{h} \\ &=\lim_{h\to0} \dfrac{\dfrac{1}{x+h}-\dfrac{1}{x}}{h} \\ &=\lim_{h\to0} \dfrac{1}{h}\dfrac{x-(x+h)}{(x+h)x} \\ &=\lim_{h\to0} \dfrac{-1}{(x+h)x} =-\,\dfrac{1}{x^2} \end{aligned}\]

       We can also solve using the second method. \[\begin{aligned} g'(x)&=\lim_{z\to x} \dfrac{g(z)-g(x)}{z-x} \\ &=\lim_{z\to x} \dfrac{\dfrac{1}{z}-\dfrac{1}{x}}{z-x} \\ &=\lim_{z\to x} \dfrac{1}{z-x}\dfrac{x-z}{zx} \\ &=\lim_{z\to x} \dfrac{-1}{zx} =-\,\dfrac{1}{x^2} \end{aligned}\]

    2. Use the derivative to find \(g'(4)\).

       \(g'(4)=-\,\dfrac{1}{16}\)

       We simply plug \(x=4\) into \(g'(x)=-\,\dfrac{1}{x^2}\): \[ g'(4)=-\,\dfrac{1}{4^2}=-\,\dfrac{1}{16} \]

    3. Find the tangent line to \(y=g(x)\) at \(x=4\).

       \(y=-\,\dfrac{1}{16}x+\dfrac{1}{2}\)

       Since \(g(4)=\dfrac{1}{4}\) and \(g'(4)=-\,\dfrac{1}{16}\), the tangent line is: \[\begin{aligned} y&=g(4)+g'(4)(x-4) \\ &=\dfrac{1}{4}-\dfrac{1}{16}(x-4) =-\,\dfrac{1}{16}x+\dfrac{1}{2} \end{aligned}\]

    4. Use the derivative to find \(g'(p)\) at a general point \(x=p\).

       \(g'(p)=-\,\dfrac{1}{p^2}\)

       We simply plug \(x=p\) into \(g'(x)=-\,\dfrac{1}{x^2}\): \[ g'(p)=-\,\dfrac{1}{p^2} \]

    5. Find the tangent line to \(y=g(x)\) at a general point \(x=p\).

       \(y=-\,\dfrac{1}{p^2}x+\dfrac{2}{p}\)

       Since \(g(p)=\dfrac{1}{p}\) and \(g'(p)=-\,\dfrac{1}{p^2}\), the tangent line is: \[\begin{aligned} y&=g(p)+g'(p)(x-p) \\ &=\dfrac{1}{p}-\dfrac{1}{p^2}(x-p) =-\,\dfrac{1}{p^2}x+\dfrac{2}{p} \end{aligned}\]

18. Consider the function \(f(x)=\dfrac{1}{\sqrt{x}}\).

    1. Find the derivative \(f'(x)\) as a function of \(x\).

       The derivative of the function \(f(x)\) is the function \(f'(x)\) given by either of the limits: \[\begin{aligned} f'(x)&=\lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} \\ &=\lim_{z\to x} \dfrac{f(z)-f(x)}{z-x} \end{aligned}\] Use whichever formula is convenient. Try both.

       \(f'(x)=-\,\dfrac{1}{2x^{3/2}}\)

       To do the limit, we put the terms over a common denominator and then multiply by the conjugate: \[\begin{aligned} f'(x)&=\lim_{h\to0} \dfrac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to0} \dfrac{\dfrac{1}{\sqrt{x+h}}-\dfrac{1}{\sqrt{x}}}{h} \\ &=\lim_{h\to0} \dfrac{1}{h}\dfrac{\sqrt{x}-\sqrt{x+h}}{\sqrt{x+h}\,\sqrt{x}} \\ &=\lim_{h\to0} \dfrac{1}{h}\dfrac{\sqrt{x}-\sqrt{x+h}}{\sqrt{x+h}\,\sqrt{x}} \cdot\dfrac{\sqrt{x}+\sqrt{x+h}}{\sqrt{x}+\sqrt{x+h}} \\ &=\lim_{h\to0} \dfrac{(x)-(x+h)}{h\sqrt{x+h}\,\sqrt{x}\,(\sqrt{x}+\sqrt{x+h})} \\ &=\lim_{h\to0} \dfrac{-1}{\sqrt{x+h}\,\sqrt{x}\,(\sqrt{x}+\sqrt{x+h})} \\ &=\lim_{h\to0} \dfrac{-1}{2\sqrt{x}^3} =-\,\dfrac{1}{2x^{3/2}} \end{aligned}\]

       We can also compute the limit using the second method. To do the limit, we multiply by the conjugate: \[\begin{aligned} f'(x)&=\lim_{z\to x} \dfrac{f(z)-f(x)}{z-x} \\ &=\lim_{z\to x} \dfrac{\dfrac{1}{\sqrt{z}}-\dfrac{1}{\sqrt{x}}}{z-x} \\ &=\lim_{z\to x} \dfrac{1}{z-x}\,\dfrac{\sqrt{x}-\sqrt{z}}{\sqrt{z}\,\sqrt{x}} \\ &=\lim_{z\to x} \dfrac{1}{z-x}\,\dfrac{\sqrt{x}-\sqrt{z}}{\sqrt{z}\,\sqrt{x}} \cdot\dfrac{\sqrt{x}+\sqrt{z}}{\sqrt{x}+\sqrt{z}} \\ &=\lim_{z\to x} \dfrac{x-z}{(z-x)\sqrt{z}\,\sqrt{x}\,(\sqrt{x}+\sqrt{z})} \\ &=\lim_{z\to x} \dfrac{-1}{\sqrt{z}\,\sqrt{x}\,(\sqrt{x}+\sqrt{z})} \\ &=\lim_{z\to x} \dfrac{-1}{2\sqrt{x}^3} =-\,\dfrac{1}{2x^{3/2}} \end{aligned}\]

    2. Use the derivative to find \(f'(4)\).

       \(f'(4)=-\,\dfrac{1}{16}\)

       We simply plug \(x=4\) into \(f'(x)=-\,\dfrac{1}{2x^{3/2}}\): \[ f'(4)=-\,\dfrac{1}{2\cdot4^{3/2}}=-\,\dfrac{1}{16} \]

    3. Find the tangent line to \(y=f(x)\) at \(x=4\).

       \(y=-\,\dfrac{1}{16}x+\dfrac{1}{4}\)

       Since \(f(4)=\dfrac{1}{2}\) and \(f'(4)=-\,\dfrac{1}{16}\), the tangent line is: \[\begin{aligned} y&=f(4)+f'(4)(x-4) \\ &=\dfrac{1}{2}-\dfrac{1}{16}(x-4) =-\,\dfrac{1}{16}x+\dfrac{1}{4} \end{aligned}\]

    4. Use the derivative to find \(f'(p)\) at a general point \(x=p\).

       \(f'(p)=-\,\dfrac{1}{2p^{3/2}}\)

       We simply plug \(x=p\) into \(f'(x)=-\,\dfrac{1}{2x^{3/2}}\): \[ f'(p)=-\,\dfrac{1}{2p^{3/2}} \]

    5. Find the tangent line to \(y=f(x)\) at a general point \(x=p\).

       \(y=-\,\dfrac{1}{2p^{3/2}}x+\dfrac{3}{2\sqrt{p}}\)

       Since \(f(p)=\dfrac{1}{\sqrt{p}}\) and \(f'(p)=-\,\dfrac{1}{2p^{3/2}}\), the tangent line is: \[\begin{aligned} y&=f(p)+f'(p)(x-p) \\ &=\dfrac{1}{\sqrt{p}}-\,\dfrac{1}{2p^{3/2}}(x-p) =-\,\dfrac{1}{2p^{3/2}}x+\dfrac{3}{2\sqrt{p}} \end{aligned}\]

19. If \(f(x)=4x^3\), find its derivative \(f'(x)\). Use it to find \(f'(4)\).

    The derivative of the function \(f(x)\) is given by either limit: \[ f'(x)=\lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h} =\lim_{z\to x} \dfrac{f(z)-f(x)}{z-x} \] For the first method you will need: \[ (x+h)^3=x^3+3x^2h+3xh^2+h^3 \] For the second method you will need: \[ z^3-x^3=(z-x)(z^2+zx+x^2) \]

    \(f'(x)=12x^2\).
    \(f'(4)=192\)

    \[\begin{aligned} f'(x)&=\lim_{h\to0} \dfrac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to0} \dfrac{4(x+h)^3-4x^3}{h} \\ &=\lim_{h\to0} \dfrac{4(x^3+3x^2h+3xh^2+h^3)-4x^3}{h} \\ &=\lim_{h\to0} \dfrac{4x^3+12x^2h+12xh^2+4h^3-4x^3}{h} \\ &=\lim_{h\to0} (12x^2+12xh+4h^2) =12x^2 \end{aligned}\]

    \[\begin{aligned} f'(4)=192 \end{aligned}\]

    db 

    We use the identity \[ z^3-x^3=(z-x)(z^2+xz+x^2) \] \[\begin{aligned} f'(x)&=\lim_{z\to x} \dfrac{f(z)-f(x)}{z-x} \\ &=\lim_{z\to x} \dfrac{4z^3-4x^3}{z-x} \\ &=\lim_{z\to x} \dfrac{4(z-x)(z^2+xz+x^2)}{z-x} \\ &=\lim_{z\to x} (4z^2+4xz+4x^2) =12x^2 \end{aligned}\]

20. If \(j(x)=x^{1/3}\), find its derivative \(j'(x)\). Use it to find \(j'(8)\).

    The derivative of the function \(j(x)\) is given by either limit: \[ j'(x)=\lim_{h\to 0} \dfrac{j(x+h)-j(x)}{h} =\lim_{z\to x} \dfrac{j(z)-j(x)}{z-x} \] You will need to appply the identity: \[ (a-b)(a^2+ab+b^2)=a^3-b^3 \] when \(a\) and \(b\) are cube roots.

    \(j'(x)=\dfrac{1}{3x^{2/3}}\).
    
    \(j'(8)=\dfrac{1}{12}\).

    To do the limit we multiply by a generalized conjugate using \[ (a-b)(a^2+ab+b^2)=a^3-b^3 \] where \(a\) and \(b\) are cube roots. \[\begin{aligned} f'(x)&=\lim_{h\to0} \dfrac{j(x+h)-j(x)}{h} \\ &=\lim_{h\to0} \dfrac{(x+h)^{1/3}-(x)^{1/3}}{h} \\ &=\lim_{h\to0} \dfrac{(x+h)^{1/3}-(x)^{1/3}}{h}\cdot \dfrac{(x+h)^{2/3}+x^{1/3}(x+h)^{1/3}+x^{2/3}}{(x+h)^{2/3}+x^{1/3}(x+h)^{1/3}+x^{2/3}} \\ &=\lim_{h\to0} \dfrac{x+h-x}{h\big[(x+h)^{2/3}+x^{1/3}(x+h)^{1/3}+x^{2/3}\big]} \\ &=\lim_{h\to0} \dfrac{1}{(x+h)^{2/3}+x^{1/3}(x+h)^{1/3}+x^{2/3}} =\dfrac{1}{3x^{2/3}} \end{aligned}\] \[\begin{aligned} f'(8)=\dfrac{1}{12} \end{aligned}\]

    db 

    We again do the limit by multipling by a generalized conjugate using \[ (a-b)(a^2+ab+b^2)=a^3-b^3 \] where \(a\) and \(b\) are cube roots. \[\begin{aligned} f'(x)&=\lim_{z\to x} \dfrac{j(z)-j(x)}{z-x} \\ &=\lim_{z\to x} \dfrac{z^{1/3}-x^{1/3}}{z-x} \\ &=\lim_{z\to x} \dfrac{z^{1/3}-x^{1/3}}{z-x}\cdot \dfrac{z^{2/3}+x^{1/3}z^{1/3}+x^{2/3}}{z^{2/3}+x^{1/3}z^{1/3}+x^{2/3}} \\ &=\lim_{z\to x} \dfrac{z-x}{(z-x)(z^{2/3}+x^{1/3}z^{1/3}+x^{2/3})} \\ &=\lim_{z\to x} \dfrac{1}{z^{2/3}+x^{1/3}z^{1/3}+x^{2/3}} =\dfrac{1}{3x^{2/3}} \end{aligned}\]

---

Find the following rates of change.

21. Duke Skywater fires the rockets on the Centurion Eagle so that its position at time \(t\) is \(x(t)=2t^3-5t^2\). Find it's velocity and acceleration at time \(t\) and at time \(t=2\).

    If a particle is at position \(x(t)\), at time \(t\), then its velocity, at time \(t\), is its derivative, \(v(t)=x'(t)\), and its acceleration, at time \(t\), is the derivative of the velocity, \(a(t)=v'(t)\).

    You will need the formulas: \[\begin{aligned} (t+h)^2&=t^2+2th+h^2 \\ (t+h)^3&=t^3+3t^2h+3th^2+h^3 \end{aligned}\]

    \(\begin{aligned} v(t)&=6t^2-10t&v(2)&=4 \\ a(t)&=12t-10&a(2)&=14 \end{aligned}\)

    We compute the velocity by differentiating the position: \[\begin{aligned} v(t)&=x'(t) =\lim_{h\to 0} \dfrac{x(t+h)-x(t)}{h} \\ &=\lim_{h\to 0} \dfrac{[2(t+h)^3-5(t+h)^2]-[2t^3-5t^2]}{h} \\ &=\lim_{h\to 0} \dfrac{[2(t^3+3t^2h+3th^2+h^3)-5(t^2+2th+h^2)]-[2t^3-5t^2]}{h} \\ &=\lim_{h\to 0} \dfrac{(6t^2h+6th^2+2h^3)-(10th+5h^2)}{h} \\ &=\lim_{h\to 0} [(6t^2+6th+2h^2)-(10t+5h)]=6t^2-10t \\ \end{aligned}\] So the velocity is \(v(t)=6t^2-10t\).
    We compute the acceleration by differentiating the velocity: \[\begin{aligned} a(t)&=v'(t) =\lim_{h\to 0} \dfrac{v(t+h)-v(t)}{h} \\ &=\lim_{h\to 0} \dfrac{[6(t+h)^2-10(t+h)]-[6t^2-10t]}{h} \\ &=\lim_{h\to 0} \dfrac{[6(t^2+2th+h^2)-10(t+h)]-[6t^2-10t]}{h} \\ &=\lim_{h\to 0} \dfrac{(12th+6h^2)-10(h)}{h} \\ &=\lim_{h\to 0} [(12t+6h)-10]=12t-10 \\ \end{aligned}\] So the acceleration is \(a(t)=12t-10\).
    We evaluate both at \(t=2\): \[\begin{aligned} v(2)&=6\cdot2^2-10\cdot2=4 \\ a(2)&=12\cdot2-10=14 \end{aligned}\]

22. A Porsche 918 Spyder (racecar) travels with position function \(x(t)=t^{1/4}\). Find the car's velocity as a functions of time \(t\). Then find the car's position and velocity at \(t=16\).

    You will need to multiply by a conjugate twice.

    \(\begin{aligned} x(t)&=t^{1/4}&v(16)&=2 \\ v(t)&=\dfrac{1}{4t^{3/4}}&v(16)&=\dfrac{1}{32} \\ \end{aligned}\)

    The car's velocity, \(v\), is the derivative of \(x(t)\). We will multiply by a conjugate twice: \[\begin{aligned} v(t)&=x'(t)=\lim_{h\to 0} \dfrac{x(t+h)-x(t)}{h} \\ &=\lim_{h\to0} \dfrac{(t+h)^{1/4}-t^{1/4}}{h} \\ &=\lim_{h\to0} \dfrac{(t+h)^{1/4}-t^{1/4}}{h} \cdot\dfrac{(t+h)^{1/4}+t^{1/4}}{(t+h)^{1/4}+t^{1/4}} \\ &=\lim_{h\to0} \dfrac{(t+h)^{1/2}-t^{1/2}}{h[(t+h)^{1/4}+t^{1/4}]} \\ &=\lim_{h\to0} \dfrac{(t+h)^{1/2}-t^{1/2}}{h[(t+h)^{1/4}+t^{1/4}]} \cdot\dfrac{(t+h)^{1/2}+t^{1/2}}{(t+h)^{1/2}+t^{1/2}} \\ &=\lim_{h\to0} \dfrac{(t+h)-t} {h[(t+h)^{1/4}+t^{1/4}][(t+h)^{1/2}+t^{1/2}]} \\ &=\lim_{h\to0} \dfrac{1} {[(t+h)^{1/4}+t^{1/4}][(t+h)^{1/2}+t^{1/2}]} \\ &=\dfrac{1} {[2t^{1/4}][2t^{1/2}]} =\dfrac{1}{4t^{3/4}} \end{aligned}\] At \(t=16\), the position and velocity are: \[\begin{aligned} x(t)&=t^{1/4}&v(16)&=16^{1/4}=2 \\ v(t)&=\dfrac{1}{4t^{3/4}}\quad&v(16)&=\dfrac{1}{4\cdot16^{3/4}} \\ &&&=\dfrac{1}{4\cdot2^3}=\dfrac{1}{32} \end{aligned}\]

    db 

23. The amount of water in a bucket at time \(t\) is given by \(B(t)=t\sqrt{t}\). What is the rate at which the bucket is filling as a function of \(t\)? What is the rate at \(t=9\)?

    The rate of change of any quantity, \(Q(t)\), at time \(t=a\) is the derivative of the quantity at \(t=a\), that is \(Q'(a)\).

    \(B'(t)=\dfrac{3}{2}\sqrt{t}\)
    
    \(B'(9)=\dfrac{9}{2}\)

    We first rewrite the function as \(B(t)=t^{3/2}\). We do the limit by multiplying by the conjugate. \[\begin{aligned} B'(t)&=\lim_{h\to 0} \dfrac{B(t+h)-B(t)}{h} \\ &=\lim_{h\to 0} \dfrac{(t+h)^{3/2}-t^{3/2}}{h} \\ &=\lim_{h\to 0} \dfrac{(t+h)^{3/2}-t^{3/2}}{h} \cdot\dfrac{(t+h)^{3/2}+t^{3/2}}{(t+h)^{3/2}+t^{3/2}} \\ &=\lim_{h\to 0} \dfrac{(t+h)^3-t^3}{h[(t+h)^{3/2}+t^{3/2}]} \\ &=\lim_{h\to 0} \dfrac{3t^2h+3th^2+h^3}{h[(t+h)^{3/2}+t^{3/2}]} \\ &=\lim_{h\to 0} \dfrac{3t^2+3th+h^2}{(t+h)^{3/2}+t^{3/2}} \\ &=\dfrac{3t^2}{t^{3/2}+t^{3/2}} =\dfrac{3t^2}{2t^{3/2}} =\dfrac{3}{2}t^{1/2} =\dfrac{3}{2}\sqrt{t} \end{aligned}\] So, the rate at \(t=9\) is: \[\begin{aligned} B'(9)=\dfrac{3}{2}\sqrt{9}=\dfrac{9}{2} \end{aligned}\]

    db 

d. The First Derivative Test for Maxima and Minima

1
24. Let \(f(x)=\dfrac{1}{5}x^5-16x\).

    1. Find its derivative \(f'(x)\) using the limit definition.

       The derivative is the limit: \[ f'(x)=\lim_{h\to0} \dfrac{f(x+h)-f(x)}{h} \]

       \(f'(x)=x^4-16\)

       The derivative is the limit: \[\begin{aligned} f'(x)&=\lim_{h\to0} \dfrac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to0} \dfrac{ \left[\dfrac{1}{5}(x+h)^5-16(x+h)\right]-\left[\dfrac{1}{5}x^5-16x\right] }{h} \\ &=\lim_{h\to0} \dfrac{1}{h}\left[\dfrac{1}{5}(x^5+5x^4h+10x^3h^2+10x^2h^3+5xh^4+h^5)\right. \\ &\qquad\qquad\left.-16x-16h-\dfrac{1}{5}x^5+16x\right] \\ &=\lim_{h\to0} \dfrac{1}{h}\left[\dfrac{1}{5}(5x^4h+10x^3h^2+10x^2h^3+5xh^4+h^5) -16h\right] \\ &=\lim_{h\to0} \left[\dfrac{1}{5}(5x^4+10x^3h+10x^2h^2+5xh^3+h^4)-16\right] \\ &=x^4-16 \end{aligned}\]

       db 

    2. Where is \(f(x)\) increasing or decreasing?

       The function is increasing when \(f'(x)\) is positive. It is decreasing when \(f'(x)\) is negative.

       \(f(x)\) is increasing on \((-\infty,-2]\) and \([2,\infty)\).
       \(f(x)\) is decreasing on \([-2,2]\).

       We factor the derivative: \[ f'(x)=x^4-16=(x^2+4)(x+2)(x-2) \] This is zero when \(x=-2\) or \(x=2\). So we need to check the sign of the derivative \(f'(x)=x^4-16\) on each of the intervals: \((-\infty,-2]\), \([-2,2]\) and \([2,\infty)\). We evaluate \(f'(x)\) at a point in each interval and observe its sign: \[\begin{aligned} f'(-3)&=(-3)^4-16=65 \gt 0 \\ f'(0)&=0^4-16=-16 \lt 0\\ f'(3)&=(3)^4-16=65 \gt 0 \\ \end{aligned}\] So the function is increasing on \((-\infty,-2]\) and \([2,\infty)\) but decreasing on \([-2,2]\).

       db 

    3. Find the local maxima and minima of \(f(x)\) and any horizontal inflection points.

       By the First Derivative Test, a local maximum occurs at a point where the function changes from increasing to decreasing, and a local minimum occurs at a point where the function changes from decreasing to increasing

       The maximum value is \(f(-2)=\dfrac{128}{5}\) and the minimum value is \(f(2)=-\,\dfrac{128}{5}\). There are no horizontal inflection points.

       We previously found the function is increasing on \((-\infty,-2]\) and \([2,\infty)\) but decreasing on \([-2,2]\). A local maximum occurs at a point where the function changes from increasing to decreasing, and a local minimum occurs at a point where the function changes from decreasing to increasing. So, we conclude that \(f(x)\) has a local maximum at \(x=-2\) and a local minimum at \(x=2\). The function values of \(f(x)=\dfrac{1}{5}x^5 - 16x\) are: \[\begin{aligned} f(-2)&=\dfrac{1}{5}(-2)^5 - 16(-2)=\dfrac{128}{5} \\ f(2)&=\dfrac{1}{5}(2)^5 - 16(2)=-\,\dfrac{128}{5} \end{aligned}\] So the maximum value is \(f(-2)=\dfrac{128}{5}\) and the minimum value is \(f(2)=-\,\dfrac{128}{5}\). There are no horizontal inflection points.

       db 

25. Let \(f(x)=x^4-8x^3+18x^2\).

    1. Find its derivative \(f'(x)\) using the limit definition.

       The derivative is the limit: \[ f'(x)=\lim_{h\to0} \dfrac{f(x+h)-f(x)}{h} \]

       \(f'(x)=4x^3-24x^2+36x\)

       The derivative is the limit: \[\begin{aligned} f'(x)&=\lim_{h\to0} \dfrac{f(x+h)-f(x)}{h} \\ &=\lim_{h\to0} \dfrac{1}{h} \left[\rule{0pt}{10pt}(x+h)^4-8(x+h)^3+18(x+h)^2\right. \\ &\qquad\qquad\left.\rule{0pt}{10pt}-\,(x^4-8x^3+18x^2)\right] \\ &=\lim_{h\to0} \dfrac{1}{h} \left[\rule{0pt}{10pt}(x^4+4x^3h+6x^2h^2+4xh^3+h^4)\right. \\ &\qquad\qquad-\,8(x^3+3x^2h+3xh^2+h^3) \\ &\qquad\qquad\left.+18(x^2+2xh+h^2)-(x^4-8x^3+18x^2)\rule{0pt}{10pt}\right] \\ &=\lim_{h\to0} \dfrac{1}{h}\left[\rule{0pt}{10pt}(4x^3h+6x^2h^2+4xh^3+h^4)\right. \\ &\qquad\qquad\left.\rule{0pt}{10pt}-\,8(3x^2h+3xh^2+h^3)+18(2xh+h^2)\right] \\ &=\lim_{h\to0} \left[\rule{0pt}{10pt}(4x^3+6x^2h+4xh^2+h^3)\right. \\ &\qquad\qquad\left.-\rule{0pt}{10pt}\,8(3x^2+3xh+h^2)+18(2x+h)\right] \\ &=4x^3-24x^2+36x \end{aligned}\]

       db 

    2. Where is \(f(x)\) increasing or decreasing?

       The function is increasing when \(f'(x)\) is positive. It is decreasing when \(f'(x)\) is negative.

       \(f(x)\) is decreasing on \((-\infty,0]\).
       \(f(x)\) is increasing on \([0,3]\) and \([3,\infty)\).

       We factor the derivative: \[\begin{aligned} f'(x)&=4x^3-24x^2+36x \\ &=4x(x^2-6x+9)=4x(x-3)^2 \end{aligned}\] This is zero when \(x=0\) or \(x=3\). So we need to check the sign of the derivative \(f'(x)\) on each of the intervals: \((-\infty,0]\), \([0,3]\) and \([3,\infty)\). We evaluate \(f'(x)=4x(x-3)^2\) at a point in each interval and observe its sign: \[\begin{aligned} f'(-1)&=4(-1)(-1-3)^2=-64\lt 0 \\ f'(1)&=4(1)(1-3)^2=16 \gt 0\\ f'(4)&=4(4)(4-3)^2=16 \gt 0 \end{aligned}\] So the function is decreasing on \((-\infty,0]\) and increasing on \([0,3]\) and \([3,\infty)\).

       db 

    3. Find the local maxima and minima of \(f(x)\) and any horizontal inflection points.

       By the First Derivative Test, a local maximum occurs at a point where the function changes from increasing to decreasing, and a local minimum occurs at a point where the function changes from decreasing to increasing. A horizontal inflection point occurs if the function stays increasing or decreasing on both sides of the critical point.

       \(x=0\) is a local minimum and \(f(0)=0\).
       \(x=3\) is a horizontal inflection point and \(f(3)=27\).

       We previously found the function is decreasing on \((-\infty,0]\) and increasing on \([0,3]\). So \(x=0\) is a local minimum and \(f(0)=0\). We also found the function is increasing on \([0,3]\) and \([3,\infty]\). So \(x=3\) is a horizontal inflection point and \[ f(3)=3^4-8\cdot3^3+18\cdot3^2=3^3(3-8+6)=27 \]