10. Derivatives and Tangent Lines

a. Derivative at a Point

1. Definition

In the chapter on Applications of Limits, in discussing rates of change, the same limit occurs every time. Consequently, we give it a name:

The derivative of the function \(f(x)\) at the point \(x=a\), denoted by \(f'(a)\), is the limit: \[ f'(a)=\lim_{h\rightarrow 0} \dfrac{f(a+h)-f(a)}{h} \]

The figure shows the derivative is the slope of the tangent line regarded as the limit of the slopes of the secant lines.

The derivative of the function \(f(x)\) at the point \(x=a\) can also be written as the limit: \[ f'(a)=\lim_{x\rightarrow a} \dfrac{f(x)-f(a)}{x-a} \]

Let \(x=a+h\). Then \(x-a=h\) and \(x\rightarrow a\) is the same as \(h\rightarrow 0\). Consequently: \[ \lim_{x\rightarrow a} \dfrac{f(x)-f(a)}{x-a} =\lim_{h\rightarrow 0} \dfrac{f(a+h)-f(a)}{h}=f'(a) \]

The above formula gives the derivative as the limit of the difference (or change) in the \(y\) values, \(\Delta f=f(x)-f(a)\), divided by the difference (or change) in the \(x\) values, \(\Delta x=x-a\); the rise over the run. Consequently, we frequently say the derivative is a limit of a difference quotient: \[ f'(a)=\lim_{\Delta x\to0}\dfrac{\Delta f}{\Delta x} \] This leads to several alternate notations for the derivative: \[ f'(a)=\dfrac{df}{dx}(a)=\left.\dfrac{df}{dx}\right|_a =\dfrac{dy}{dx}(a)=\left.\dfrac{dy}{dx}\right|_a \] This is called differential notation while \(dx\) and \(dy=df\) are called the differentials which can be thought of as infinitesimal changes in \(x\) and \(y\). More details will be given in a later chapter on Differentials.

Find the derivative of \(f(x)=x^2\) at \(x=3\).

We write out and compute the limit definition with \(a=3\): \[\begin{aligned} f'(3)&=\lim_{h\rightarrow 0} \dfrac{f(3+h)-f(3)}{h} =\lim_{h\rightarrow 0} \dfrac{(3+h)^2-(3)^2}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{3^2+6h+h^2-3^2}{h} =\lim_{h\rightarrow 0} \dfrac{6h+h^2}{h} \\ &=\lim_{h\rightarrow 0} (6+h) =6 \end{aligned}\]

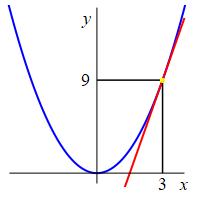
This time we use the alternate formula with \(a=3\): \[\begin{aligned} f'(3)&=\lim_{x\rightarrow 3} \dfrac{f(x)-f(3)}{x-3} =\lim_{x\rightarrow 3} \dfrac{x^2-3^2}{x-3} \\ &=\lim_{x\rightarrow 3} (x+3) =6 \end{aligned}\]

If \(f(x)=\dfrac{3}{x}\), compute \(\dfrac{df}{dx}(6)\). Compute it by \(2\) methods.

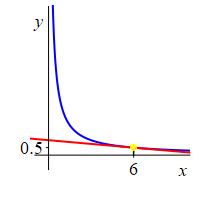
\(\dfrac{df}{dx}(6)=-\,\dfrac{1}{12}\)

We write out and compute the limit definition with \(a=6\): \[\begin{aligned} \dfrac{df}{dx}(6)&=\lim_{h\rightarrow 0} \dfrac{f(6+h)-f(6)}{h} =\lim_{h\rightarrow 0} \dfrac{\dfrac{3}{6+h}-\dfrac{3}{6}}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{1}{h}\dfrac{3[6-(6+h)]}{6(6+h)} =\lim_{h\rightarrow 0} \dfrac{-3h}{6h(6+h)} \\ &=\lim_{h\rightarrow 0} \dfrac{-1}{2(6+h)} =-\,\dfrac{1}{12} \end{aligned}\]

This time we use the alternate formula with \(a=6\): \[\begin{aligned} \dfrac{df}{dx}(6)&=\lim_{x\rightarrow 6} \dfrac{f(x)-f(6)}{x-6} =\lim_{x\rightarrow 6} \dfrac{\dfrac{3}{x}-\dfrac{1}{2}}{x-6} \\ &=\lim_{x\rightarrow 6} \dfrac{1}{x-6}\dfrac{6-x}{2x} =\lim_{x\rightarrow 6} \dfrac{-1}{2x} =-\,\dfrac{1}{12} \end{aligned}\]

Does it matter which formula we use for the derivative? No! We can use whichever formula seems easier. Of course, we can't know which will be easier until we do them. So we just pick one.

We will develop better ways to compute derivatives, called Derivative Rules, in the next chapter. For now we restrict to simple functions for which the limits are straightforward.

10. Derivatives and Tangent Lines

a. Derivative at a Point

1. Definition

Heading