10. Derivatives and Tangent Lines

a. Derivative at a Point

2. Applications

All the Applications of Limits for rates of change, can now be done using derivatives.

Velocity

If a particle is at position \(x(t)\) as a function of time \(t\), then its velocity at time \(t=a\), is the derivative of the position at \(t=a\), that is \(v(a)=x'(a)\).

Between \(t=0\) and \(t=4\), a girl takes a walk from \(x=0\) to \(x=16\) and back. Her position at time \(t\) is \(x(t)=16-(t-2)^4\). What is her velocity at \(t=3\)?

\(v(3)=x'(3)=-4\)

The velocity is the derivative of \(x(t)\) at \(t=3\). On the \(3^\text{rd}\) line, we cancel the \(16\)'s and expand the numerator. On the \(4^\text{th}\) line we cancel the \(1\)'s in the numerator. On the \(5^\text{th}\) line we cancel the \(h\) from the denominator. \[\begin{aligned} v(3)&=x'(3)=\lim_{h\rightarrow 0} \dfrac{x(3+h)-x(3)}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{[16-(1+h)^4]-[16-(1)^4]}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{-(1+4h+6h^2+4h^3+h^4)+1}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{-(4h+6h^2+4h^3+h^4)}{h} \\ &=\lim_{h\rightarrow 0} -(4+6h+4h^2+h^3)=-4 \\ \end{aligned}\] The velocity is negative because the girl has reversed directions.

Slope

The slope of the tangent line to a function, \(f(x)\), at a point \(x=a\) is the derivative of the function at \(x=a\), that is \(m=f'(a)\).

Find the slope of the tangent line to the function, \(f(x)=6x^2-x^3\), at \(x=3\).

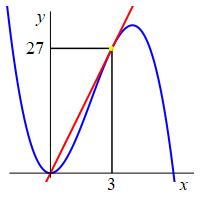
ex_tan_slope_deriv_pt_appl

Slope: \(m=f'(3)=9\)

The slope is the derivative of \(f(x)\) at \(x=3\).
On the \(3^\text{rd}\) line, we expand \((3+h)^2\) and \((3+h)^3\).
On the \(4^\text{th}\) line, we cancel and combine terms in the numerator.
On the \(5^\text{th}\) line we cancel the \(54\) in the numerator and then the \(h\) from the denominator. \[\begin{aligned} m&=f'(3)=\lim_{h\rightarrow 0} \dfrac{f(3+h)-f(3)}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{[6(3+h)^2-(3+h)^3]-[6\cdot3^2-3^3]}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{[6(9+6h+h^2)-(27+27h+9h^2+h^3)]-[54-27]}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{54 + 36h + 6h^2 -27 - 27h -9h^2 -h^3 - 27}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{9h-3h^2 -h^3}{h} \\ &=\lim_{h\rightarrow 0} (9-3h-h^2)=9 \end{aligned}\]

Other Rates of Change

The rate of change of any quantity, \(Q(t)\), at time \(t=a\) is the derivative of the quantity at \(t=a\), that is \(Q'(a)\).

The volume of water in a rain gauge at time \(t\) is given by \(V(t)=\sqrt{t}\). What is the rate, \(V'(4)\), at which the gauge is filling at \(t=4\)?

\(V'(4)=\dfrac{1}{4}\)

The rate at which the gauge is filling is the derivative \(V'(4)\).
On the \(2^\text{nd}\) line, we multiply the numerator and denominator by the conjugate.
On the \(3^\text{rd}\) line, we expand in the numerator using difference of squares.
On the \(4^\text{th}\) line we simplify the numerator and cancel the \(h\) from the denominator. \[\begin{aligned} V'(4)&=\lim_{h\rightarrow 0} \dfrac{R(4+h)-R(4)}{h} =\lim_{h\rightarrow 0} \dfrac{\sqrt{4+h}-\sqrt{4}}{h} \\ &=\lim_{h\rightarrow 0} \dfrac{(\sqrt{4+h}-\sqrt{4})}{h} \dfrac{(\sqrt{4+h}+\sqrt{4})}{(\sqrt{4+h}+\sqrt{4})} \\ &=\lim_{h\rightarrow 0} \dfrac{(4+h)-(4)}{h(\sqrt{4+h}+\sqrt{4})} \\ &=\lim_{h\rightarrow 0} \dfrac{1}{\sqrt{4+h}+\sqrt{4}}=\dfrac{1}{4} \\ \end{aligned}\]

© MYMathApps

Supported in part by NSF Grant #1123255