3. Intuitive Limits and Continuity

Exercises

a. What my Algebra Teacher Never Told me!

Simplify the function \(f(x)=\dfrac{3+2x-x^2}{x+1}\) and graph it.

\( f(x)=\left\{\begin{matrix} 3-x & \text{if} & x\ne-1 \\ \text{undefined} & \text{if} & x=-1 \end{matrix}\right. \)

We factor and cancel: \[\begin{aligned} f(x)&=\dfrac{3+2x-x^2}{x+1} \\ &=\dfrac{-(x-3)(x+1)}{x+1}=-x+3 \end{aligned}\] This is true if and only if \(x \ne -1\). So, the correct simplification is: \[ f(x)=\left\{\begin{matrix} 3-x & \text{if} & x\ne-1 \\ \text{undefined} & \text{if} & x=-1 \end{matrix}\right. \]

The graph has a hole at \(x=-1\).

abs
Simplify the function \(g(x)=\dfrac{x^3-2x^2}{x-2}\) and graph it.

\( f(x)=\left\{\begin{matrix} x^2 & \text{if} & x\ne2 \\ \text{undefined} & \text{if} & x=2 \end{matrix}\right. \)

We factor and cancel to get: \[\begin{aligned} f(x)&=\dfrac{x^3-2x^2}{x-2} \\ &=\dfrac{x^2(x-2)}{x-2}=x^2 \end{aligned}\] This is true if and only if \(x \ne 2\). So, the correct simplification is: \[ f(x)=\left\{\begin{matrix} x^2 & \text{if} & x\ne2 \\ \text{undefined} & \text{if} & x=2 \end{matrix}\right. \]

The graph has a hole at \(x=2\).

abs
Simplify the function \(h(x)=\dfrac{x^2-5x+6}{x^2-9}\).

\[ h(x)=\left\{\begin{matrix} \dfrac{x-2}{x+3} & \text{if} & x\ne-3,3 \\[2pt] \text{undefined} & \text{if} & x=-3,3 \end{matrix}\right. \]

We factor the numerator and denominator and simplify to get: \[ h(x)=\dfrac{x^2-5x+6}{x^2-9}=\dfrac{(x-3)(x-2)}{(x-3)(x+3)} =\dfrac{x-2}{x+3} \] The simplified function is undefined at \(x=-3\) because we would be dividing by \(0\). (The point, \(x=-3\), is called a vertical asymptote.) However, the original function, \(h(x)\), is also undefined at \(x=3\) -- there is a hole in the graph. So the correct simplification is: \[ h(x)=\left\{\begin{matrix} \dfrac{x-2}{x+3} & \text{if} & x\ne-3,3 \\[2pt] \text{undefined} & \text{if} & x=-3,3 \end{matrix}\right. \]

The graph has a hole at \(x=3\).

abs

b. Intuitive Definitions

For the function whose graph is shown, find \[ \lim_{x\to3^-}f(x) \qquad \lim_{x\to3^+}f(x) \qquad \text{and} \qquad f(3) \] Does \(\displaystyle \lim_{x\to3}f(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?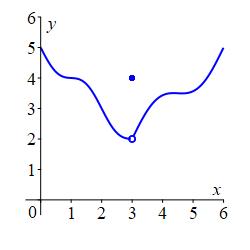

The limit from the left is the height \(f(x)\) approaches as \(x\) approaches \(3\) from the left, i.e. \(x\) is less than \(3\) but getting very close to \(3\).
The limit from the right is the value \(f(x)\) approaches as \(x\) approaches \(3\) from the right, i.e. \(x\) is greater than \(3\) but getting very close to \(3\).
The value of \(f(x)\) at \(x=3\) is \(f(3)\) if it is defined.
The (\(2\)-sided) limit exists if the limits from the left and right exist and are equal: \[ \lim_{x\to 3^-}f(x)=\lim_{x\to 3^+}f(x)=L \] We then write: \[ \lim_{x\to 3}f(x)=L \] \(f(x)\) is continuous from the left at \(x=3\) if \(\displaystyle \lim_{x\to 3^-}f(x)=f(3)\).
\(f(x)\) is continuous from the right at \(x=3\) if \(\displaystyle \lim_{x\to 3^+}f(x)=f(3)\).
\(f(x)\) is continuous at \(x=3\) if \(\displaystyle \lim_{x\to 3^-}f(x)=\lim_{x\to 3^+}f(x)=f(3)\).

\(\displaystyle \lim_{x\to 3^-}f(x)=2\)
\(\displaystyle \lim_{x\to 3^+}f(x)=2\)
\(f(3)=4\)
\(\displaystyle \lim_{x\to3}f(x)=2\)
The function is neither continous from the left nor continuous from the right nor continuous.

\(\displaystyle \lim_{x\to 3^-}f(x)=2\) because the curve on the left goes to height \(2\) as \(x\) goes to \(3\).
\(\displaystyle \lim_{x\to 3^+}f(x)=2\) because the curve on the right goes to height \(2\) as \(x\) goes to \(3\).
\(f(3)=4\) because the solid dot above \(x=3\) is at height \(4\).
Since \(\displaystyle \lim_{x\to 3^-}f(x)=\lim_{x\to 3^+}f(x)=2\), we find \(\displaystyle \lim_{x\to3}f(x)\) exists, and its value is \(2\).
The function is neither continuous from the left, nor continuous from the right, nor continuous because \(\displaystyle \lim_{x\to3^+}f(x)\ne f(3)\ne\lim_{x\to3^+}f(x)\).

abs
For the function whose graph is shown, find \[ \lim_{x\to2^-}f(x) \qquad \lim_{x\to2^+}f(x) \qquad \text{and} \qquad f(2) \] Does \(\displaystyle \lim_{x\to2}f(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?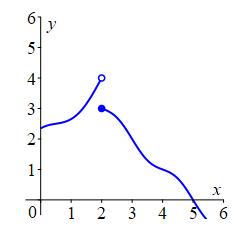

\(\displaystyle \lim_{x\to 2^-}f(x)=4\).
\(\displaystyle \lim_{x\to 2^+}f(x)=3)\).
\(f(2)=3\)
\(\displaystyle \lim_{x\to2}f(x)\) does not exist.
The function is continuous from the right only.

\(\displaystyle \lim_{x\to 2^-}f(x)=4\) because the curve on the left goes to height \(4\) as \(x\) goes to \(2\).
\(\displaystyle \lim_{x\to 2^+}f(x)=3\) because the curve on the right goes to height \(3\) as \(x\) goes to \(2\).
\(f(2)=3\) because the solid dot above \(x=2\) is at height \(3\).
Since \(\displaystyle \lim_{x\to 2^-}f(x)\ne\lim_{x\to 2^+}f(x)\), we find \(\displaystyle \lim_{x\to2}f(x)\) does not exist.
The function is continuous from the right because \(\displaystyle \lim_{x\to2^+}f(x)=f(2)=3\). However it is not continuous from the left nor continuous because \(\displaystyle \lim_{x\to2^-}f(x)=4\ne3\).

abs
For the function whose graph is shown, find \[ \lim_{x\to5^-}f(x) \qquad \lim_{x\to5^+}f(x) \qquad \text{and} \qquad f(5) \] Does \(\displaystyle \lim_{x\to5}f(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?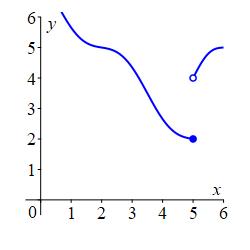

\(\displaystyle \lim_{x\to 5^-}f(x)=2\).
\(\displaystyle \lim_{x\to 5^+}f(x)=4\).
\(f(5)=2\).
\(\displaystyle \lim_{x\to5}f(x)\) does not exist.
The function is continous from the left only.

\(\displaystyle \lim_{x\to 5^-}f(x)=2\) because the curve on the left goes to height \(2\) as \(x\) goes to \(5\).
\(\displaystyle \lim_{x\to 5^+}f(x)=4\) because the curve on the right goes to height \(4\) as \(x\) goes to \(5\).
\(f(5)=2\) because the solid dot above \(x=5\) is at height \(2\).
Since \(\displaystyle \lim_{x\to 5^-}f(x)\ne\lim_{x\to 5^+}f(x)\), we find \(\displaystyle \lim_{x\to5}f(x)\) does not exist.
The function is continous from the left, because \(\displaystyle \lim_{x\to5^-}f(x)=f(5)=2\). However it is not continuous from the right nor continuous because \(\displaystyle \lim_{x\to2^+}f(x)=4\ne2\).

abs
For the function \(f(x)=\dfrac{3+2x-x^2}{x+1}\) find: \[ \lim_{x\to-1^-}f(x) \qquad \lim_{x\to-1^+}f(x) \qquad \text{and} \qquad f(-1) \] Does \(\displaystyle \lim_{x\to-1}f(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?

\(f(x)\) is simplified in a previous problem. Use it.

\(\displaystyle \lim_{x\to-1^-}f(x)=\lim_{x\to-1^+}f(x)=4\)
\(f(-1)\) is undefined.
The \(2\)-sided limit exists and \(\displaystyle \lim_{x\to-1^-}f(x)=4\).
\(f(x)\) is not continuous from the left or right or continuous.

In a previous problem we found: \[ f(x)=\left\{\begin{matrix} 3-x & \text{if} & x\ne-1 \\ \text{undefined} & \text{if} & x=-1 \end{matrix}\right. \] So \(f(-1)\) is undefined and the limits for \(f(x)\) are the same as those for \(3-x\). For the limit from the left, we compute: \[ \lim_{x\to-1^-}f(x)=\lim_{x\to-1^-}\dfrac{-(x-3)(x+1)}{x+1}=\lim_{x\to-1^-}(3-x)=4 \] (This is called factor and cancel.) Similarly for the limit from the right, we compute: \[ \lim_{x\to-1^+}f(x)=\lim_{x\to-1^+}(3-x)=4 \] Since \(\displaystyle \lim_{x\to-1^-}f(x)=\lim_{x\to-1^+}f(x)=4\), we have \(\displaystyle \lim_{x\to-1}f(x)\) exists, and its value is \(\displaystyle \lim_{x\to-1}f(x)=4\). Since \(f(-1)\) does not exist, \(f(x)\) is not continuous from the left or right or continuous.

abs
For the function \(g(x)=\dfrac{x^3-2x^2}{x-2}\) find: \[ \lim_{x\to2^-}g(x) \qquad \lim_{x\to2^+}g(x) \qquad \text{and} \qquad g(2) \] Does \(\displaystyle \lim_{x\to2}g(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?

\(g(x)\) is simplified in a previous problem. Use it.

\(\displaystyle \lim_{x\to2^-}g(x)=\lim_{x\to2^+}g(x)=4\)
\(g(2)\) is undefined.
The \(2\)-sided limit exists and \(\displaystyle \lim_{x\to2^-}g(x)=4\).
\(g(x)\) is not continuous from the left or right or continuous.

In a previous problem we found: \[ g(x)=\left\{\begin{matrix} x^2 & \text{if} & x\ne2 \\ \text{undefined} & \text{if} & x=2 \end{matrix}\right. \] So \(g(2)\) is undefined and the limits for \(g(x)\) are the same as those for \(x^2\). For the limit from the left, we compute: \[ \lim_{x\to2^-}g(x)=\lim_{x\to2^-}\dfrac{x^2(x-2)}{x-2}=\lim_{x\to1^-}x^2=4 \] (This is called factor and cancel.) Similarly for the limit from the right, we compute: \[ \lim_{x\to2^+}g(x)=\lim_{x\to2^+}x^2=4 \] Since \(\displaystyle \lim_{x\to2^-}g(x)=\lim_{x\to2^+}g(x)=4\), we have \(\displaystyle \lim_{x\to2}g(x)\) exists, and its value is \(\displaystyle \lim_{x\to2}g(x)=4\). Since \(g(2)\) does not exist, \(g(x)\) is not continuous from the left or right or continuous.

abs
For the function \( h(x)=\left\{ \begin{matrix} x+2 & \text{if} & x\lt3 \\ 5 & \text{if} & x=3 \\ 7-x & \text{if} & x\gt3 \end{matrix}\right. \) find: \[ \lim_{x\to3^-}h(x) \qquad \lim_{x\to3^+}h(x) \qquad \text{and} \qquad h(3) \] Does \(\displaystyle \lim_{x\to3}h(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?

\(\displaystyle \lim_{x\to3^-}h(x)=5\)
\(\displaystyle \lim_{x\to3^+}h(x)=4\)
\(h(3)=5\)
\(\displaystyle \lim_{x\to3}h(x)\) does not exist.
\(f(x)\) is continuous from the left but not continuous from the right nor continuous.

To compute the limit from the left, we plug in numbers less than \(3\) using the formula for \(x \lt 3\). This gives: \[\begin{aligned} x&= 2.9& &2.99& &2.999& &\to 3 \\ h(x)&= 4.9& &4.99& &4.999& &\to 5 \end{aligned}\] So, as \(x\) approaches \(3\), \(y\) approaches \(5\). Therefore: \[ \lim_{x\to3^-}h(x)=5 \] Similarly, to compute the limit from the right, we plug in numbers greater than \(3\) using the formula for \(x \gt 3\). This gives: \[\begin{aligned} x&= 3.1& &3.01& &3.001& &\to 3 \\ h(x)&= 3.9& &3.99& &3.999& &\to 4 \end{aligned}\] Therefore: \[ \lim_{x\to3^+}h(x)=4 \] To find \(h(3)\), we use the second formula to get \(h(3)=5\).

\(\displaystyle \lim_{x\to3}h(x)\) does not exist, because \(\displaystyle \lim_{x\to3^-}h(x)=5\) and \(\displaystyle \lim_{x\to3^+}h(x)=4\) which are not equal. The function is continous from the left, because \(\displaystyle \lim_{x\to3^-}h(x)=h(3)=5\). It is not continuous from the right nor continuous since \(\displaystyle \lim_{x\to3^+}h(x)=4\) and \(h(3)=5\) which are not equal.

abs
For the function \( p(x)=\left\{ \begin{matrix} x^2 & \text{if} & x\lt2 \\ 4 & \text{if} & x=2 \\ 8-x^2 & \text{if} & x\gt2 \end{matrix}\right. \) find: \[ \lim_{x\to2^-}p(x) \qquad \lim_{x\to2^+}p(x) \qquad \text{and} \qquad p(2) \] Does \(\displaystyle \lim_{x\to2}p(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?

\(\displaystyle \lim_{x\to2^-}p(x) =\lim_{x\to2^+}p(x) =p(2)=4\)
\(2\)-sided limit exists and \(\displaystyle \lim_{x\to2}p(x)=4\).
\(p(x)\) is continuous and hence also continuous from the left and right.

To compute the limit from the left, we plug in numbers less than \(2\) using the formula for \(x \lt 2\). This gives: \[\begin{aligned} x&= 1.9& &1.99& &1.999& &\to 2 \\ p(x)&= 3.61& &3.9601& &3.996001& &\to 4 \end{aligned}\] So, as \(x\) approaches \(2\), \(y\) approaches \(4\). Therefore: \[ \lim_{x\to2^-}p(x)=4 \] Similarly, to compute the limit from the right, we plug in numbers greater than \(2\) using the formula for \(x \gt 2\). This gives: \[\begin{aligned} x&= 2.1& &2.01& &2.001& &\to 2 \\ p(x)&= 3.59& &3.9599& &3.995999& &\to 4 \end{aligned}\] Therefore: \[ \lim_{x\to2^+}p(x)=4 \] To find \(p(2)\), we use the second formula to get \(p(2)=4\). Since \(\displaystyle \lim_{x\to2^-}p(x)=\lim_{x\to2^+}p(x)=p(2)=4\), the function is continuous and consequently continuous from the left and right and the \(2\)-sided limit exists and \(\displaystyle \lim_{x\to2}p(x)=4\).

abs
For the function \( q(x)=\left\{ \begin{matrix} x+1 & \text{if} & x\lt5 \\ x+2 & \text{if} & x=5 \\ x+3 & \text{if} & x\gt5 \end{matrix}\right. \) find: \[ \lim_{x\to 5^-}q(x) \qquad \lim_{x\to 5^+}q(x) \qquad \text{and} \qquad q(5) \] Does \(\displaystyle \lim_{x\to 5}q(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?

\(\displaystyle \lim_{x\to 5^-}q(x)=6\)
\(\displaystyle \lim_{x\to 5^+}q(x)=8\)
\(q(5)=7\)
\(\displaystyle \lim_{x\to5}q(x)\) does not exist.
\(q(x)\) is neither continuous from the left, nor the right nor continuous.

To compute the limit from the left, we plug in numbers less than \(5\) using the formula for \(x \lt 5\). This gives: \[\begin{aligned} x&= 4.9& &4.99& &4.999& &\to 5 \\ q(x)&= 5.9& &5.99& &5.999& &\to 6 \end{aligned}\] So, as \(x\) approaches \(5\), \(y\) approaches \(6\). Therefore: \[ \lim_{x\to5^-}q(x)=6 \] Similarly, to compute the limit from the right, we plug in numbers greater than \(5\) using the formula for \(x \gt 5\). This gives: \[\begin{aligned} x&= 5.1& &5.01& &5.001& &\to 5 \\ q(x)&= 8.1& &8.01& &8.001& &\to 8 \end{aligned}\] Therefore: \[ \lim_{x\to5^+}q(x)=8 \] To find \(q(5)\), we use the second formula to get \(q(5)=7\). \(\displaystyle \lim_{x\to5}q(x)\) does not exist since \(\displaystyle \lim_{x\to5^-}q(x)=6\ne\lim_{x\to5^+}=8\). Since \(\displaystyle \lim_{x\to5^-}q(x)=6\ne\lim_{x\to5^+}q(x)=8\ne q(2)=4\), the function is neither continous, nor continuous from the left, nor continuous from the right.

abs
For the function \( k(x)=\left\{ \begin{matrix} 3-x & \text{if} & x\lt2 \\ x-1 & \text{if} & x\gt2 \end{matrix}\right. \) find: \[ \lim_{x\to 2^-}k(x) \qquad \lim_{x\to 2^+}k(x) \qquad \text{and} \qquad k(2) \] Does \(\displaystyle \lim_{x\to 2}k(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?

\(\displaystyle \lim_{x\to 2^-}k(x)=\lim_{x\to 2^+}k(x)=1\)
\(k(2)\) is undefined.
\(\displaystyle \lim_{x\to2}k(x)\) does exist, and its value is \(1\).
The function is not continuous.

To compute the limit from the left, we plug in numbers less than \(2\) using the formula for \(x \lt 2\). This gives: \[\begin{aligned} x&= 1.9& &1.99& &1.999& &\to 2 \\ k(x)&= 1.1& &1.01& &1.001& &\to 1 \end{aligned}\] So, as \(x\) approaches \(2\), \(y\) approaches \(1\). Therefore: \[ \lim_{x\to2^-}k(x)=1 \] Similarly, to compute the limit from the right, we plug in numbers greater than \(2\) using the formula for \(x \gt 2\). This gives: \[\begin{aligned} x&= 2.1& &2.01& &2.001& &\to 2 \\ k(x)&= 1.1& &1.01& &1.001& &\to 1 \end{aligned}\] Therefore: \[ \lim_{x\to2^+}k(x)=1 \] \(k(2)\)is undefined, because there is no value given for \(x=2\). Since \(\displaystyle \lim_{x\to2^-}k(x)=\lim_{x\to2^+}k(x)=1\), \(\displaystyle \lim_{x\to2}\) exists, and its value is \(\displaystyle \lim_{x\to2}=1\). The function is not continuous because \(f(2)\) does not exist.

abs
For the function \( l(x)=\left\{ \begin{matrix} x-1 & \text{if} & x\lt7 \\ -3 & \text{if} & x=7 \\ 4-x & \text{if} & x\gt7 \end{matrix}\right. \) find: \[ \lim_{x\to 7^-}l(x) \qquad \lim_{x\to 7^+}l(x) \qquad \text{and} \qquad l(7) \] Does \(\displaystyle \lim_{x\to 7}l(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?

\(\displaystyle \lim_{x\to 7^-}l(x)=6\)
\(\displaystyle \lim_{x\to 7^+}l(x)=l(7)=-3\)
\(\displaystyle \lim_{x\to7}l(x)\) does not exist.
The function is continuous from the right but not continuous from the left nor continuous.

To compute the limit from the left, we plug in numbers less than \(7\) using the formula for \(x \lt 7\). This gives: \[\begin{aligned} x&= 6.9& &6.99& &6.999& &\to 7 \\ l(x)&= 5.9& &5.99& &5.999& &\to 6 \end{aligned}\] So, as \(x\) approaches \(7\), \(y\) approaches \(6\). Therefore: \[ \lim_{x\to7^-}l(x)=6 \] Similarly, to compute the limit from the right, we plug in numbers greater than \(7\) using the formula for \(x \gt 7\). This gives: \[\begin{aligned} x&=&7.1&&7.01&&7.001&&\to&&7& \\ l(x)&=&-3.1&&-3.01&&-3.001&&\to&&-3& \end{aligned}\] Therefore: \[ \lim_{x\to7^+}l(x)=-3 \] To find \(l(7)\), we use the second formula to get \(l(7)=-3\). Since \(\displaystyle \lim_{x\to7^-}l(x)=6\ne l(7)=\lim_{x\to7^+}l(x)=-3\), \(\displaystyle \lim_{x\to7}l(x)\) does not exist, \(l(x)\) is not continuous from the left nor continuous, but it is continuous from the right.

abs
For the function \( m(x)=\left\{ \begin{matrix} 3-x & \text{if} & x\lt3 \\ 3+x & \text{if} & x\ge3 \end{matrix}\right. \) find: \[ \lim_{x\to 3^-}m(x) \qquad \lim_{x\to 3^+}m(x) \qquad \text{and} \qquad m(3) \] Does \(\displaystyle \lim_{x\to 3}m(x)\) exist and if so give its value.
Is the function continuous from the left, continuous from the right or continuous?

\(\displaystyle \lim_{x\to 3^-}m(x)=0\)
\(\displaystyle \lim_{x\to 3^+}m(x)=m(3)=6\)
So \(\displaystyle \lim_{x\to3}m(x)\) does not exist.
The function is continuous from the right but not continuous from the left nor continuous.

To compute the limit from the left, we plug in numbers less than \(3\) using the formula for \(x \lt 3\). This gives: \[\begin{aligned} x&= 2.9& &2.99& &2.999& &\to 3 \\ m(x)&= 0.1& &0.01& &0.001& &\to 0 \end{aligned}\] So, as \(x\) approaches \(3\), \(y\) approaches \(0\). Therefore: \[ \lim_{x\to3^-}m(x)=0 \] Similarly, to compute the limit from the right, we plug in numbers greater than \(3\) using the formula for \(x \ge 3\). This gives: \[\begin{aligned} x&= 3.1& &3.01& &3.001& &\to 3 \\ m(x)&= 6.1& &6.01& &6.001& &\to 6 \end{aligned}\] Therefore: \[ \lim_{x\to3^+}m(x)=6 \] To find \(m(3)\) we use the formula for \(x \ge 3\) to get \(m(3)=6\). Since \(\displaystyle \lim_{x\to3^-}m(x)\ne\lim_{x\to3^+}m(x)\), \(\displaystyle \lim_{x\to3}m(x)\) does not exist. Since \(\displaystyle \lim_{x\to3^-}m(x)=0\ne m(3)=6\), \(m(x)\) is not continuous from the left nor continuous. However, since \(\displaystyle \lim_{x\to3^+}m(x)=m(3)=6\), the function is continuous from the right.

abs

c. Tutorial on Limits and Continuity

Do the tutorial repeatedly until you have done one which is continuous, one which is continuous from the left but not continuous, one which is continuous from the right but not continuous, and one which has a \(2\)-sided limit but is not continuous.

d. Continuity on an Interval

For each function, find the interval(s) on which it is continuous.

\(f(x)=\dfrac{1}{x^2-9}\)

The function is continous as long as the denominator is defined and non-zero.

\(f(x)\) is continuous on the intervals \((-\infty,-3)\), \((-3, 3)\), and \((3,\infty)\).

Since \(f(x)\) is undefined when \(x=-3\) and when \(x=3\), those are the only points at which the function is not continuous. Therefore, the function is continuous on the intervals \((-\infty,-3)\), \((-3, 3)\), and \((3,\infty)\).

abs
\(g(x)=\dfrac{1}{\sqrt{4-x^2}}\)

The function is continous as long as the denominator is defined and non-zero.

The function is continuous on the open interval \((-2, 2)\).

\(g(x)\) is undefined when the quantity in the square root is negative or zero. It is positive when \(4-x^2 \gt 0\) or \(x^2 \lt 4\) or \(|x| \lt 2\) or \(-2 \lt x \lt 2\). This is the open interval \((-2, 2)\).

abs
\(h(x)=\dfrac{1}{x^3-27}\)

The function is continous as long as the denominator is defined and non-zero.

The function is continous in the open intervals \((-\infty, 3)\) and \((3,\infty)\).

\(h(x)\) is only undefined when \(x=3\). Therefore it is continuous on the intervals \((-\infty, 3)\) and \((3,\infty)\).

abs
\(p(x)=\sqrt{6-x}+\dfrac{1}{\sqrt{6+x}}\)

The function is continuous as long as the denominator is non-zero and the quantities in the square roots are non-negative.

The function is continuous in the open interval \((-6,6]\).

The first square root is defined when \(6-x \ge 0\) or \(x \le 6\) which is the interval \((-\infty, 6]\). The second square root is in the denominator and so is defined only when \(6+x \gt 0\) or \(x \gt -6\) which is the interval \((-6,\infty)\). The function is defined and continuous on the intersection \((-6,6]\).

abs
\(q(x)=\dfrac{x^2-4}{x^2-4x+8}\)

The function is continous as long as the denominator is defined and non-zero.

The function is continous in the interval \((-\infty, \infty)\).

Using the quadratic formula, the zeroes of the denominator are \[ x=\dfrac{4\pm\sqrt{16-32}}{2}=\dfrac{4\pm4i}{2}=2\pm2i \] Since there are no real roots, the function is defined and continuous for all \(x\). So the function is continous on the interval \((-\infty, \infty)\).

abs

e. Limits at Infinity

Compute the following limits at infinity.

\(\displaystyle \lim_{x\to\infty}\dfrac{3x}{x+1}\)

Divide the numerator and denominator by \(x\).

\(\displaystyle \lim_{x\to\infty}\dfrac{3x}{x+1}=3\).

We divide the numerator and denominator by \(x\): \[ \lim\limits_{x\to\infty}\dfrac{3x}{x+1} =\lim\limits_{x\to\infty}\dfrac{3x}{1+x}\dfrac{\;\dfrac{1}{x}\;}{\dfrac{1}{x}} =\lim\limits_{x\to\infty}\dfrac{3}{\dfrac{1}{x}+1} \] As \(x\) gets large, \(\dfrac{1}{x}\) approaches \(0\). So: \[ \lim\limits_{x\to\infty}\dfrac{3x}{x+1} =\dfrac{3}{0+1}=3 \]

abs
\(\displaystyle \lim_{x\to\infty}\dfrac{7x^2}{3x^3+3}\)

Divide the numerator and denominator by \(x^3\).

\(\displaystyle \lim_{x\to\infty}\dfrac{7x^2}{3x^3+3}=0\).

We divide the numerator and denominator by \(x^3\): \[ \lim\limits_{x\to\infty}\dfrac{7x^2}{3x^3+3} =\lim\limits_{x\to\infty}\dfrac{7x^2}{3x^3+3}\dfrac{\;\dfrac{1}{x^3}\;}{\dfrac{1}{x^3}} =\lim\limits_{x\to\infty}\dfrac{\dfrac{7}{x}}{3+\dfrac{3}{x^3}} \] As \(x\) gets large, \(\dfrac{7}{x}\) and \(\dfrac{3}{x^3}\) approach \(0\). So: \[ \lim\limits_{x\to\infty}\dfrac{7x^2}{3x^3+3} =\dfrac{0}{3+0}=0 \]

abs
\(\displaystyle \lim_{x\to\infty}\dfrac{6x^4}{3x^3+2x}\)

Divide the numerator and denominator by \(x^3\).

\(\displaystyle \lim_{x\to\infty}\dfrac{6x^4}{3x^3+2x}=\infty\).

We divide the numerator and denominator by \(x^3\): \[ \lim\limits_{x\to\infty}\dfrac{6x^4}{3x^3+2x} =\lim\limits_{x\to\infty}\dfrac{6x^4}{3x^3+2x} \dfrac{\;\dfrac{1}{x^3}\;}{\dfrac{1}{x^3}} =\lim\limits_{x\to\infty}\dfrac{6x}{3+\dfrac{2}{x^2}} \] As \(x\) gets large, \(\dfrac{2}{x^2}\) approaches \(0\). So: \[ \lim\limits_{x\to\infty}\dfrac{6x^4}{3x^3+2x} =\lim\limits_{x\to\infty}2x=\infty \]

abs
\(\displaystyle \lim_{x\to\infty}\dfrac{\sqrt{4x^2-1}}{4x+3}\)

Divide the numerator and denominator by \(x\).
Also, for \(x \gt 0\), \(\dfrac{1}{x}=\sqrt{\dfrac{1}{x^2}}\).

\(\displaystyle \lim_{x\to\infty}\dfrac{\sqrt{4x^2-1}}{4x+3}=\dfrac{1}{2}\)

We divide the numerator and denominator by \(x\): \[\begin{aligned} \lim_{x\to\infty}\dfrac{\sqrt{4x^2-1}}{4x+3} &=\lim_{x\to\infty}\dfrac{\sqrt{4x^2-1}}{4x+3} \dfrac{\;\dfrac{1}{x}\;}{\dfrac{1}{x}} \\ &=\lim_{x\to\infty}\dfrac{\sqrt{4x^2-1}}{4x+3} \dfrac{\;\dfrac{1}{\sqrt{x^2}}\;}{\dfrac{1}{x}} \\ &=\lim_{x\to\infty}\dfrac{\sqrt{4-\dfrac{1}{x^2}}}{4+\dfrac{3}{x}} \end{aligned}\] As \(x\) gets large, \(\dfrac{3}{x}\) and \(\dfrac{1}{x^2}\) approach \(0\). So: \[ \lim_{x\to\infty}\dfrac{\sqrt{4x^2-1}}{4x+3} =\dfrac{\sqrt{4}}{4}=\dfrac{1}{2} \]

abs