6. Intuitive Limits and Continuity

We begin our study of Calculus with Limits. In this chapter we want to develop an intuitive understanding of limits. In a later chapter, we will get a more precise definition.

a. What my Algebra Teacher Never Told me!

We begin with a multiple choice question you might have gotten in a high school algebra class:

Simplify the function \(f(x)=\dfrac{x^2-4}{x-2}\).

\(f(x)=x-2\)   \(f(x)=x+2\)   Undefined   None of these

Incorrect. Sorry that's not correct. Factor the numerator and cancel!

Incorrect. This is the answer you would have given in a high school algebra class, but it is not correct in a calculus class. If we factor the numerator and cancel we appear to get \[ \dfrac{x^2-4}{x-2}=\dfrac{(x+2)(x-2)}{x-2}=x+2 \] However, we cannot just cancel.
Notice \(f(x)=x+2\) is defined for all \(x\), but, \(f(x)=\dfrac{x^2-4}{x-2}\) is undefined at \(x=2\) because we would be dividing by \(0\). If we cancel, we lose the fact that \(f(x)\) is undefined at \(x=2\).

Incorrect. You are on the right track, but \(f(x)\) is defined for most \(x\).

Correct! \(f(x)=x+2\) is defined for all all \(x\). However, \(f(x)=\dfrac{x^2-4}{x-2}\) is undefined at \(x=2\) because we would be dividing by \(0\). So a correct simplification would be: \[\begin{aligned} f(x)&=\dfrac{x^2-4}{x-2}=\dfrac{(x+2)(x-2)}{x-2} \\ &=\left\{\begin{matrix} x+2 & \text{if} & x\ne2 \\ \text{undefined} & \text{if} & x=2 \end{matrix}\right. \end{aligned}\]

\(\leftarrow\leftarrow\leftarrow\) Be sure to read this after you do the exercise!

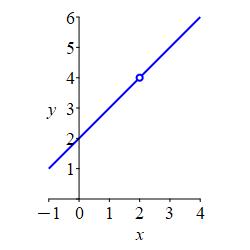
So a correct simplification in the above exercise is: \[\begin{aligned} f(x)&=\dfrac{x^2-4}{x-2}=\dfrac{(x+2)(x-2)}{x-2} \\ &=\left\{\begin{matrix} x+2 & \text{if} & x\ne2 \\ \text{undefined} & \text{if} & x=2 \end{matrix}\right. \end{aligned}\] A plot of \(f(x)\) is shown at the right.

eg_never_told
Graph of \(f(x)=\dfrac{x^2-4}{x-2}\).

The graph of \(y=x+2\) is a straight line with slope \(m=1\) and \(y\)-intercept \(b=2\) as shown at the right.
The graph of \(y=\dfrac{x^2-4}{x-2}\) is the same straight line but with a hole at \(x=2\) as shown above.

eg_never_told_wrong
Graph of \(y=x+2\).

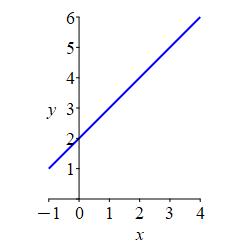
If we look at the graph, we see that as \(x\) approaches \(x=2\), the value of \(y\) approaches \(y=4\). (This is the value we get if we plug \(x=2\) into \(y=x+2\).) To capture this idea of approaching \(y=4\) even though we can never actually get there, we define the limit: \[ \lim_{x\to2}f(x) =\lim_{x\to2}\dfrac{x^2-4}{x-2} =4 \] This (intuitive) definition will be made clearer on the next page.

© MYMathApps

Supported in part by NSF Grant #1123255