6. Intuitive Limits and Continuity

We have discussed limits as \(x\) approaches a finite number. We now turn to limits at infinity.

e. Limits at Infinity

The limit of a function \(f(x)\) as \(x\) approaches \(\infty\), denoted \(\lim\limits_{x\to\infty}f(x)\), tells what number the function approaches as \(x\) gets arbitrarily large. The precise definition of the limit at infinity is in the chapter on Precise Limits. However for most of this course, it is sufficient to understand the following intuitive definition:

A function \(f(x)\) has a limit at (positive) infinity if the values of the function get closer and closer to a finite number \(L\) as \(x\) gets arbitrarily large and positive. In that case, we say \(\lim\limits_{x\to\infty}f(x)\) exists and is equal to \(L\), and we write: \[ \lim\limits_{x\to\infty}f(x)=L \] Similarly, a function \(f(x)\) has a limit at negative infinity if the values of the function get closer and closer to a finite number \(L\) as \(x\) gets arbitrarily large and negative. In that case, we say \(\lim\limits_{x\to-\infty}f(x)\) exists and is equal to \(L\), and we write: \[ \lim\limits_{x\to-\infty}f(x)=L \] If a function has a limit \(L\), we say it is convergent and that it converges to \(L\).
If a function does not have a limit, we say it is divergent or that it diverges.

The function \(f(x)=\dfrac{2+5\cdot2^{-x}}{1+2^{-x}}\) converges to \(2\) at \(\infty\) and converges to \(5\) at \(-\infty\). Here is the plot:

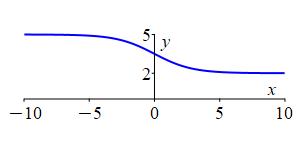
If the function diverges, it may still have an infinite limit.

If the values of a function \(f(x)\) get arbitrarily large and positive as \(x\) gets arbitrarily large, then we say the function diverges to (positive) infinity (\(+\infty\)) or that the limit is \(+\infty\) and write: \[ \lim\limits_{x\to\infty}f(x)=\infty \] If the values of a function \(f(x)\) get arbitrarily large and negative as \(x\) gets arbitrarily large, then we say the function diverges to negative infinity (\(-\infty\)) or that the limit is \(-\infty\) and write: \[ \lim\limits_{x\to\infty}f(x)=-\infty \] There are similar definitions for limits at \(-\infty\) which are \(\pm\infty\).
If a function is divergent but does not diverge to either \(\infty\) or \(-\infty\), then we say it is oscillatory divergent.

We emphasize that to say the limit is positive or negative infinity does not say that the limit exists! It merely says the way in which it does not exist, i.e. the way in which it diverges.

The function \(f(x)=-5+x^2\) diverges to \(\infty\) because \(-5+x^2\) gets arbitrarily large and positive as \(x\) gets large. Its plot is:

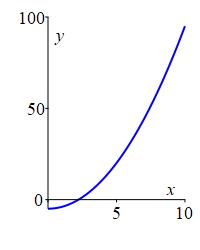
The function \(f(x)=5-x^2\) diverges to \(-\infty\) because \(5-x^2\) gets arbitrarily large and negative as \(x\) gets large. Its plot is:

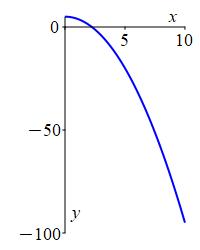
It is certainly possible to diverge without diverging to \(\infty\) or \(-\infty\).

Since the function \(f(x)=2\sin(x)\) oscillates between \(2\) and \(-2\), it does not converge; it diverges. However, it does not diverge to \(\infty\) or \(-\infty\). So it is oscillatory divergent. Its plot is:

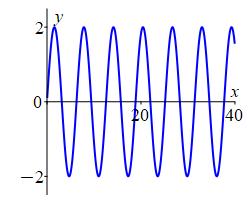
Find the limit \(\displaystyle \lim\limits_{x\to\infty}\dfrac{2x}{4+x}\).

Divide the numerator and denominator by \(x\).

\(\displaystyle \lim_{x\to\infty}\dfrac{2x}{4+x}=2\).

We divide the numerator and denominator by \(x\): \[ \lim\limits_{x\to\infty}\dfrac{2x}{4+x} =\lim\limits_{x\to\infty}\dfrac{2}{\dfrac{4}{x}+1} \] As \(x\) gets large, \(\dfrac{1}{x}\) approaches \(0\). So: \[ \lim\limits_{x\to\infty}\dfrac{2x}{4+x} =\dfrac{2}{0+1}=2 \]

Techniques for computing limits appear in the next chapter.

6. Intuitive Limits and Continuity

e. Limits at Infinity

Heading