6. Intuitive Limits and Continuity

b. Intuitive Definitions

2. 2-Sided Limits and Continuity

Given a function, \(f(x)\), and a point, \(x=a\), we have defined

\(f(a)\), the value at \(x=a\),
\(\displaystyle \lim_{x\to a^-}f(x)\), the limit as \(x\) approaches \(a\) from the left, and
\(\displaystyle \lim_{x\to a^+}f(x)\), the limit as \(x\) approaches \(a\) from the right.

In principle, these three numbers could all be different or one or more might not even exist. However, there are special words to describe the situations when \(2\) or \(3\) of these three numbers are equal.

If \(\displaystyle \lim_{x\to a^-}f(x)=\lim_{x\to a^+}f(x)=L\), then we say the (\(2\)-sided) limit exists and is equal to \(L\) and we write: \[ \lim_{x\to a}f(x)=L \]
If \(\displaystyle \lim_{x\to a^-}f(x)=f(a)\), then we say the \(f(x)\) is continuous from the left.
If \(\displaystyle \lim_{x\to a^+}f(x)=f(a)\), then we say the \(f(x)\) is continuous from the right.
If \(\displaystyle \lim_{x\to a^-}f(x) =\lim_{x\to a^+}f(x)=f(a)\), then we say \(f(x)\) is continuous. Equivalently: \[ \lim_{x\to a}f(x)=f(a) \]

If we just say limit, we mean the \(2\)-sided limit.

Continuous from the left
but not continuous.

Continuous from the right
but not continuous.

\(2\)-sided limit exists
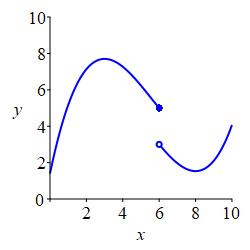
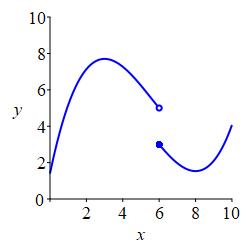
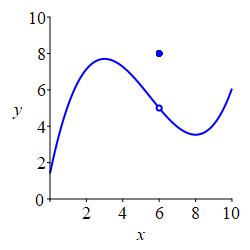
but not continuous.

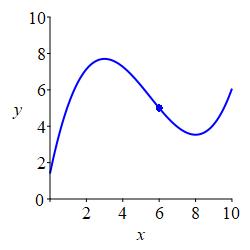
We say a (\(2\)-sided) limit is positive infinity if both the left and right limits are \(\infty\). We also say \(f(x)\) diverges to \(\infty\) and write: \[ \lim_{x\to a}f(x)=\infty \]

We say a (\(2\)-sided) limit is negative infinity if both the left and right limits are \(-\infty\). We also say \(f(x)\) diverges to \(-\infty\) and write: \[ \lim_{x\to a}f(x)=-\infty \]

The limit does not exists but
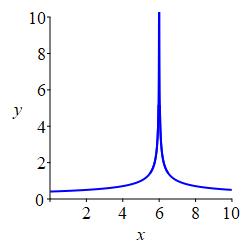
gets arbitrarily large and positive. \[ \lim_{x\to 6} f(x)=\infty \]

The limit does not exists but
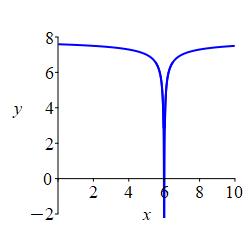
gets arbitrarily large and negative. \[ \lim_{x\to 6} f(x)=-\infty \]

To say a limit is \(\pm\infty\) does not say the limit exists, it merely says the way in which it diverges!

Click the refresh button to get a new plot.

For the function plotted, compute each quantity or say Yes or No to each question.

Hint: First find and

Does the (\(2\)-sided) limit, , exist?
Yes No

The (2-sided) limit exists when the limit from the left is equal to the limit from the right.

That's right! exists because .

Perfect! but . They are not equal.

Sorry. Read the hint. Try again.

I can't understand your answer. It may have been typed wrong. I am expecting an integer, infinity, -infinity or undefined.

You need to enter an answer before checking.

exists because .

does not exist because while which are not equal.
If the (\(2\)-sided) limit exists, give its value. If it does not exist, enter infinity, -infinity or undefined.
\(=\,\)

When the (2-sided) limit exists, it is equal to the limit from the left and the limit from the right.
When it does not exist, it is \(\infty\) when the graph goes up forever on both sides and it is \(-\infty\) when the graph goes down forever on both sides. Otherwise, it is undefined.

That's right! \(=\;\) because .

Way to go! does not exist and is neither \(\infty\) nor \(-\infty\).

Sorry. Read the hint. Try again.

I can't understand your answer. It may have been typed wrong. I am expecting an integer, infinity, -infinity or undefined.

You need to enter an answer before checking.

\(=\) because .

is undefined because it does not exist and it is neither \(\infty\) nor \(-\infty\).
Is \(f(x)\) continuous from the left at ?
Yes No

\(f(x)\) is continuous from the left when the limit from the left is equal to the value of the function.

Super! \(f(x)\) is continuous from the left because .

On the mark! \(f(x)\) is not continuous from the left because but . They are not equal.

Sorry. Read the hint. Try again.

I can't understand your answer. It may have been typed wrong. I am expecting an integer, infinity, -infinity or undefined.

You need to enter an answer before checking.

\(f(x)\) is continuous from the left because .

\(f(x)\) is not continuous from the left because while which are not equal.
Is \(f(x)\) continuous from the right at ?
Yes No

\(f(x)\) is continuous from the right when the limit from the right is equal to the value of the function.

Super! \(f(x)\) is continuous from the right because .

On the mark! \(f(x)\) is not continuous from the right because but . They are not equal.

Sorry. Read the hint. Try again.

I can't understand your answer. It may have been typed wrong. I am expecting an integer, infinity, -infinity or undefined.

You need to enter an answer before checking.

\(f(x)\) is continuous from the right because .

\(f(x)\) is not continuous from the right because while which are not equal.
Is \(f(x)\) continuous at ?
Yes No

\(f(x)\) is continuous when the limit from the left, the limit from the right and the value of the function are all equal.

Super! \(f(x)\) is continuous because .

On the mark! \(f(x)\) is not continuous because and and which are not all equal.

Sorry. Read the hint. Try again.

I can't understand your answer. It may have been typed wrong. I am expecting an integer, infinity, -infinity or undefined.

You need to enter an answer before checking.

\(f(x)\) is continuous because .

\(f(x)\) is not continuous because and and which are not all equal.

Click the refresh button to get a new piecewise function.

For the piecewise function shown, compute each quantity or say Yes or No to each question.

Hint: First find and

Does the (\(2\)-sided) limit, , exist?
Yes No

The (2-sided) limit exists when the limit from the left is equal to the limit from the right.

That's right! exists because .

Perfect! but . They are not equal.

Sorry. Read the hint. Try again.

I can't understand your answer. It may have been typed wrong. I am expecting an integer, infinity, -infinity or undefined.

You need to enter an answer before checking.

exists because .

does not exist because while which are not equal.
If the (\(2\)-sided) limit exists, give its value. If it does not exist, enter infinity, -infinity or undefined.

When the (2-sided) limit exists, it is equal to the limit from the left and the limit from the right.
When it does not exist, it is \(\infty\) when the function approaches \(\infty\) on both sides and it is \(-\infty\) when the function approaches \(-\infty\) on both sides. Otherwise, it is undefined.

That's right! \(=\) because .

Way to go! does not exist and is not \(\infty\) nor \(-\infty\).

Sorry. Read the hint. Try again.

I can't understand your answer. It may have been typed wrong. I am expecting an integer, infinity, -infinity or undefined.

You need to enter an answer before checking.

\(=\) because .

is undefined because it does not exist and it is neither \(\infty\) nor \(-\infty\).
Is \(f(x)\) continuous from the left at ?
Yes No

\(f(x)\) is continuous from the left when the limit from the left is equal to the value of the function.

Super! \(f(x)\) is continuous from the left because .

On the mark! \(f(x)\) is not continuous from the left because but . They are not equal.

Sorry. Read the hint. Try again.

I can't understand your answer. It may have been typed wrong. I am expecting an integer, infinity, -infinity or undefined.

You need to enter an answer before checking.

\(f(x)\) is continuous from the left because .

\(f(x)\) is not continuous from the left because while which are not equal.
Is \(f(x)\) continuous from the right at ?
Yes No

\(f(x)\) is continuous from the right when the limit from the right is equal to the value of the function.

Super! \(f(x)\) is continuous from the right because .

On the mark! \(f(x)\) is not continuous from the right because but . They are not equal.

Sorry. Read the hint. Try again.

I can't understand your answer. It may have been typed wrong. I am expecting an integer, infinity, -infinity or undefined.

You need to enter an answer before checking.

\(f(x)\) is continuous from the right because .

\(f(x)\) is not continuous from the right because while which are not equal.
Is \(f(x)\) continuous at ?
Yes No

\(f(x)\) is continuous when the limit from the left, the limit from the right and the value of the function are all equal.

Super! \(f(x)\) is continuous because .

On the mark! \(f(x)\) is not continuous because and and . They are not all equal.

Sorry. Read the hint. Try again.

I can't understand your answer. It may have been typed wrong. I am expecting an integer, infinity, -infinity or undefined.

You need to enter an answer before checking.

\(f(x)\) is continuous because .

\(f(x)\) is not continuous because and and which are not all equal.

The following Maplets will help you identify the function value and the \(1\)-sided limits and help you determine whether the limit exists and whether the function is continuous from \(1\) or \(2\) sides (requires Maple on the computer where this is executed). The first two are equivalent to the tutorial on the next page.

Left and Right Limits and Continuity, given a Graph Rate It

Left and Right Limits and Continuity, given a Formula Rate It

Left and Right Limits and Continuity, given Numeric Data Rate It

6. Intuitive Limits and Continuity

b. Intuitive Definitions

2. 2-Sided Limits and Continuity

Heading