MY Math Apps Calculus 2:
Integral Calculus

A Web Based, Interactive, Multimedia Calculus

Doing, Not Just Viewing

Learn Integral Calculus intuitively with the interactive MYMathApps Calculus 2 online textbook

Benefits of MYMACalc 2 over Other Texts

Many students have a great deal of difficulty visualizing in three dimensions. 3D graphics, both static and animated, are designed to help with this difficulty. Animations are also helpful with visualizing other concepts.

• In discussing Volumes by Slicing, students see the solid, a single slice and an animation of the slices accumulating to form the solid.
• In discussing Volumes of Revolution, students see the solid, a single slice, an animation of a single slice revolving so they can determine if it produces a disk, washer or cylinder and an animation of the revolved slices accumulating to form the solid.
• In discussing Surface Area of Revolution, students see animations of the curve revolving into the surface, a single segment of the curve revolving into a frustum of a cone and the frustums accumulating to form the surface.
• In various applications of integration, (such as center of mass) students see Riemann Sums being used to derive an integral formula, which is then computed using the Fundamental Theorem of Calculus,
• In learning to plot polar functions, students can see the polar graph being drawn, instead of just the final plot.
• In the section on Slope Fields for Differential Equations, students see a solution curve superimposed on the the slope field and see it move as the initial condition changes.
• In the section on Taylor Series, students see animations of the Taylor polynomials converging to the original function.

MYMACalc 2 covers some material in a different order or with different emphasis than many standard books:

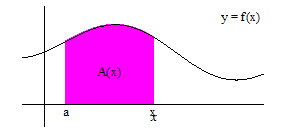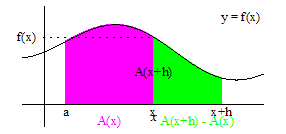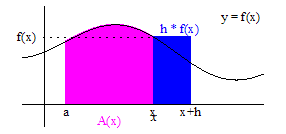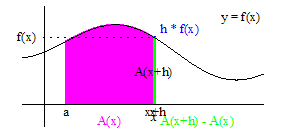
• The Fundamental Theorem of Calculus is first introduced in the context of antiderivatives by proving that the area under a curve, y=f(x), between a and x, denoted A_a(x), is the antiderivative of f(x) satisfying the initial condition A_a(a)=0. This is followed by the Riemann sum definition of an integral and showing that it is another way to find the area under a curve.
• MYMACalc 2 has chapters on the Techniques of Integration in one group followed by the chapters on Applications of Integration in a second group. However, they are written so that an instructor can alternate between Techniques and Applications without loss of continuity.
• MYMACalc 2 has Area, Average Value, Mass and Center of Mass as the first Applications followed by Arc Length, Surface Area, Volume, Work, Fluid Force and Differential Equations so that students can start with the easier applications and gradually progress to the more difficult ones.
• MYMACalc 2 has Applications of Taylor Series to each of the preceding calculus concepts: Limits, Derivatives, Integrals, Numeric Series, Fundamental Constants and Differential Equations.

Benefits of an Online Text

Although primarily a standard calculus text, the online format allows for many features which are impossible in a static book:

• There are many animations directly in the pages, some of which can be modified real-time by the student.
• The text is fully hyperlinked. The material is designed to be followed linearly, with frequent side excursions for extra material such as additional examples, background information, proofs or advanced material.
• Most pages in the text cover a single topic followed by an example and an exercise. More exercises appear on a linked exercise page. Hints, answers and full solutions for the exercises toggle in dropdown regions directly below the exercise. Hopefully, students try the problems before they click on the answer or solution button. The solution is not right there in front of them as in a paper book.
• When there is an obvious way to check an answer, the check appears in a light green region at the end of the an example's solution, or in a separate drop down region after an exercise. For example:
  After solving an equation, one should check it by substituting the solution back into the equation.
  After finding an antiderivative, one should check by differentiating.
  After finding the center of mass of an object, one should check that it is inside (the convex hull of) the object.
• Sometimes there is a comment or remark about an exercise, that the author would like to make which might have given away the answer if visible in the page. In that case there is an additional button at the end of the exercise to drop down the remark. For example:
  The integral you just computed gives the area of a semi-circle. So you could have known the answer in advance.
• Many books give formulas without proof. MYMACalc proves every formula. Derivations and proofs are directly in the text when they are essential to understanding, but are frequently hidden in a drop-down region when they are not essential, so they do not obstruct the flow of the material but are still easily accessible to interested students. There are many more proofs than most textbooks.
• There are exercise pages for each chapter and the exercises are grouped by section of the chapter. Each group is hyperlinked back to the appropriate pages, to facilitate those students who like to start on the exercises and only read the chapter when they need help doing the exercises.
• There are links to the Maplets for Calculus (M4C) directly in the text. These drill the students on specific topics acting like a “Tutor without the Tutor”. Since the M4C are displayed in Java, they cannot be viewed on most mobile devices. Consequently, they are gradually being converted into browser-based tutorials which either are directly embedded in the text or appear on separate tutorial pages.
• MYMACalc works in any browser on any device, except for the Maplets for Calculus (M4C) (because they are Java based).