11. Mass and Center of Mass

b. Center of Mass

2. Bar with Non-Uniform Density

On this page, we compute the center of mass of a bar whose mass is not uniformly distributed over the bar, i.e. when the linear density \(\delta(x)\) is a function of the position \(x\) along the bar.

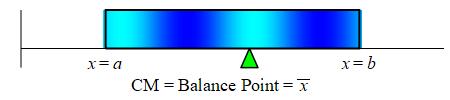
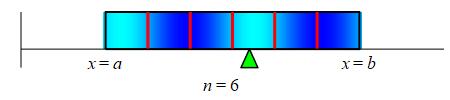
Since the density is not constant, we approximate the density of the \(i^\text{th}\) piece as \(\delta(x_i^*)\) where \(x_i^*\) is a point in the \(i^\text{th}\) region. Then the mass of the \(i^\text{th}\) region is \(m_i=\delta(x_i^*)\Delta x\). If we think of the bar as a balance beam as on the previous page, with masses \(m_1,m_2,\ldots m_n\) located at \(x_1^*,x_2^*,\ldots x_n^*\) then the center of mass is approximately at: \[ \bar{x}\approx \dfrac{M_1}{M} =\dfrac{\sum\limits_{i=1}^n m_i x_i^*}{\sum\limits_{i=1}^n m_i} =\dfrac{\sum\limits_{i=1}^n x_i^*\delta(x_i^*)\Delta x} {\sum\limits_{i=1}^n \delta(x_i^*)\Delta x} \] As the length of each piece gets smaller, the approximation gets better. So the center of mass of the bar is obtained by taking the limit as the number of pieces becomes large (\(n\to\infty\)) and hence the length of each piece gets small (\(\Delta x\to 0\)):
(Note: The limit of a quotient is the quotient of the limits.) \[ \bar{x} =\dfrac{\displaystyle\lim_{n\to\infty}\sum\limits_{i=1}^n x_i^*\delta(x_i^*)\Delta x} {\displaystyle\lim_{n\to\infty}\sum\limits_{i=1}^n \delta(x_i^*)\Delta x} \] The limit of the sum in the denominator is the integral \(\displaystyle \int_a^b \delta(x)\,dx\) which we recognize as the total mass: \[ M=\int_a^b \delta(x)\,dx \] The limit of the sum in the numerator is the integral \(\displaystyle \int_a^b x \delta(x)\,dx\) which is called the first moment of the mass: \[ M_1=\int_a^b x\delta(x)\,dx \] In terms of these, the center of mass is: \[ \bar{x}=\dfrac{M_1}{M} \] Are there higher moments?

The center of mass of a bar with linear density \(\delta(x)\) between \(x=a\) and \(x=b\) is: \[ \bar{x}=\dfrac{M_1}{M} \] where the total mass is: \[ M=\int_a^b \delta(x)\,dx \] and the first moment of the mass is: \[ M_1=\int_a^b x\delta(x)\,dx \]

The total mass was found to be \(M=40\,\text{kg}\). The first moment is: \[\begin{aligned} M_1&=\int_0^8 x\delta(x)\,dx =\int_0^8 x(1+x)\,dx \\ &=\left[\dfrac{x^2}{2}+\dfrac{x^3}{3}\right]_{x=0}^8 =\dfrac{64}{2}+\dfrac{512}{3}=\dfrac{608}{3} \text{kg-m} \end{aligned}\] So the center of mass is: \[ \bar{x}=\dfrac{M_1}{M}=\dfrac{608\,\text{kg-m}}{3}\dfrac{1}{40\,\text{kg}} =\dfrac{76}{15}\text{m}\approx 5.07\text{m} \]

You should always check that your center of mass is within the bar. In this case, \(\bar{x}\approx 5.07\,\text{m}\) is within the \(8\,\text{m}\) bar.

Now you do it:

You can practice computing Mass and Center of Mass of a Bar by using the following Maplet (requires Maple on the computer where this is executed):

Center of Mass of a Bar   Rate It