4. Line Integrals

Exercises

a. Arc Length

Find the length of the curve \(\vec r(t)=\left(3t^2+1,4\sqrt{2}t^{3/2},6t-12\right)\) from \(t=0\) to \(t=2\).

In computing \(|\vec v|\), the quantity inside the square root is a perfect square.
\(\displaystyle L=\int_A^B \,ds=\int_a^b |\vec v|\,dt\)

\(L=24\)

The velocity and its length are: \[ \vec v=(6t,6\sqrt{2}t^{1/2},6) \] \[ |\vec v|=\sqrt{36t^2+72t+36}=\sqrt{(6t+6)^2}=6t+6 \] So the arclength is: \[ L=\int_0^2 |\vec v|\,dt =\int_0^2 6t+6\,dt=\left[\rule{0pt}{10pt}3t^2+6t\right]_0^2=24 \]

as
Compute the arc length of the curve \(\vec r(t)=\left(4t^2+1,2t^2-5,4t^2\right)\) from \(t=6\) to \(t=10\)

Simplify the quantity inside the square root. \[ L=\int_A^B \,ds=\int_a^b |\vec v|\,dt \]

\(L=384\)

The velocity and its length are: \[ \vec v=(8t,4t,8t) \] \[ |\vec v|=\sqrt{64t^2+16t^2+64t^2}=\sqrt{144t^2}=12t \] So the arclength is: \[\begin{aligned} L&=\int_6^{10} |\vec v|\,dt =\int_6^{10} 12t\,dt =\left[\rule{0pt}{10pt}6t^2\right]_6^{10} \\ &=6(100-36) =384 \end{aligned}\]

as

This curve is actually a straight line from \((145,67,144)\) to \((401,195,400)\). So its length is \[\begin{aligned} L&=\sqrt{(401-145)^2+(195-67)^2+(400-144)^2} \\ &=\sqrt{256^2+128^2+256^2} =\sqrt{147456}=384 \end{aligned}\]
Compute the arc length of the helix \(y=6\sin\left(\dfrac{x}{2}\right)\), \(z=6\cos\left(\dfrac{x}{2}\right)\) between \(x=0\) and \(x=2\pi\).

For curves given with \(x\) as the parameter,
\(\displaystyle L=\int_a^b \sqrt{1+\left(\dfrac{dy}{dx}\right)^2+\left(\dfrac{dz}{dx}\right)^2}dx\)

\(L=2\pi\sqrt{10}\)

When \(x\) is the parameter, the arclength is: \[ L=\int_0^{2\pi} \sqrt{1+\left(\dfrac{dy}{dx}\right)^2+\left(\dfrac{dz}{dx}\right)^2}dx \] Here: \[ \dfrac{dy}{dx}=3\cos\left(\dfrac{x}{2}\right) \qquad \dfrac{dz}{dx}=-3\sin\left(\dfrac{x}{2}\right) \] So \[\begin{aligned} L&=\int_0^{2\pi} \sqrt{1^2+9\cos^2\left(\dfrac{x}{2}\right) +9\sin^2\left(\dfrac{x}{2}\right)}\,dx \\ &=\int_0^{2\pi} \sqrt{1+9}\,dx=2\pi\sqrt{10} \end{aligned}\]

as
Find the length of the curve \(\vec r(t)=\left(4t,\dfrac{5}{2}t^2,3t\right)\) between \(t=0\) and \(t=\dfrac{3}{4}\).

You will need a trig substitution and the integral \[ \int \sec^3\theta\,d\theta =\dfrac{1}{2}\sec\theta\tan\theta+\dfrac{1}{2}\ln|\sec\theta+\tan\theta|+C \] See the chapter on Trigonometric Integrals in Calculus 2.

\(\displaystyle L=\dfrac{75}{32}+\dfrac{5}{2}\ln2\)

The velocity and its length are: \[ \vec v=(4,5t,3) \] \[ |\vec v|=\sqrt{16+25t^2+9}=5\sqrt{t^2+1} \] So the arclength is: \[ L=\int_0^{3/4} |\vec v|\,dt =\int_0^{3/4} 5\sqrt{t^2+1}\,dt \] We now use the trig substitution \(t=\tan\theta\) and \(dt=\sec^2\theta\,d\theta\): \[\begin{aligned} L&=\int_{t=0}^{3/4} 5\sqrt{\tan^2\theta+1}\sec^2\theta\,d\theta \\ &=5\int_{t=0}^{3/4} \sec^3\theta\,d\theta \end{aligned}\] We now use the Trig Integral: \[ \int \sec^3\theta\,d\theta =\dfrac{1}{2}\sec\theta\tan\theta+\dfrac{1}{2}\ln|\sec\theta+\tan\theta|+C \] and then substitute back using \[ \tan\theta=t \quad \text{ and } \quad \sec\theta=\sqrt{\tan^2\theta+1}=\sqrt{t^2+1} \] \[\begin{aligned} L&=5\left[\dfrac{1}{2}\sec\theta\tan\theta +\dfrac{1}{2}\ln|\sec\theta+\tan\theta|\right]_{t=0}^{3/4} \\ &=5\left[\dfrac{1}{2}t\sqrt{t^2+1} +\dfrac{1}{2}\ln\left|\sqrt{t^2+1}+t\right|\right]_{t=0}^{3/4} \\ &=5\left[\dfrac{1}{2}\dfrac{3}{4}\dfrac{5}{4} +\dfrac{1}{2}\ln\left|\dfrac{5}{4}+\dfrac{3}{4}\right|\right] \\ &=\dfrac{75}{32}+\dfrac{5}{2}\ln2 \\ \end{aligned}\]

py

Compute the arc length of the helix \(\vec r(\theta)=(4\cos \theta,4\sin \theta,3\theta)\) between \(A=\left(2\sqrt{3},2,\dfrac{\pi}{2}\right)\) and \(B=\left(2,2\sqrt{3},\pi\right)\).

For what value of \(\theta\) is \(\vec r(\theta)=A\), i.e. \((4\cos \theta,4\sin \theta,3\theta)=\left(2\sqrt{3},2,\dfrac{\pi}{2}\right)\)? Likewise for \(B\). Those are the limits on the integral.

\(\displaystyle L=\dfrac{5\pi}{6}\)

To find the endpoints, we equate the \(z\) component of \(\vec r\) to the \(z\) component of \(A\) and \(B\). For \(A\), \(3\theta=\dfrac{\pi}{2}\). So \(\theta=\dfrac{\pi}{6}\). For \(B\), \(3\theta=\pi\). So \(\theta=\dfrac{\pi}{3}\). The velocity and its length are: \[ \vec{v}(\theta)=(-4\sin\theta,\,4\cos\theta,\,3) \]\[ |\vec{v}(\theta)|=\sqrt{(-4\sin\theta)^2+(4\cos\theta)^2+3^2}=\sqrt{25}=5 \] So the arclength is: \[\begin{aligned} L&=\int_{\pi/6}^{\pi/3}|\vec{v}(\theta)|\,d\theta =\int_{\pi/6}^{\pi/3}5\,d\theta \\ &=\left[\rule{0pt}{10pt}5t\right]_{\pi/6}^{\pi/3} =5\left(\dfrac{\pi}{3}-\dfrac{\pi}{6}\right) =\dfrac{5\pi}{6} \end{aligned}\]

pt

Find the arc length of the twisted cubic \(\vec r(t)=\left(t,t^2,\dfrac{2}{3}t^3\right)\) between \(A=(-3,9,-18)\) and \(B=(3,9,18)\).

What are the values of \(t\) at the \(2\) endpoints?

\(L=42\)

Looking at the \(x\) components or \(\vec r\) and \(A\) and \(B\), the values of \(t\) at the limits are \(t=-3\) and \(t=3\). The velocity and its length are: \[ \vec{v}(t)=(1,\,2t,\,2t^2) \] \[\begin{aligned} |\vec{v}(t)|&=\sqrt{1^2+(2t)^2+(2t^2)^2}=\sqrt{1+4t^2+4t^4} \\ &=\sqrt{(1+2t^2)^2}=1+2t^2 \end{aligned}\] So the arclength is: \[\begin{aligned} L&=\int_{-3}^{3}|\vec{v}(t)|\,dt =\int_{-3}^{3} 1+2t^2\,dt \\ &=\left[t+\dfrac{2}{3}t^3\right]_{-3}^{3} =\left(3+\dfrac{2}{3}(3^3)\right)-\left(-3+\dfrac{2}{3}(-3)^3\right) \\ &=2(18+3)=42 \end{aligned}\]

pt

b. Line Integrals of Scalars

Compute \(\displaystyle \int \dfrac{y^2}{xz}\,ds\) along the curve \(\vec r(t)=\left(\dfrac{1}{2}t^2,\dfrac{4}{3}t^{3/2},2t\right)\) from \(t=1\) to \(t=3\).

Set up the integral: \(\displaystyle \int_A^B f\,ds=\int_a^b f(\vec r(t))|\vec v|\,dt\)

\(\displaystyle \int_1^3 \dfrac{y^2}{xz}\,ds=\dfrac{128}{9}\)

On the curve, the integrand is \[ f=\dfrac{y^2}{xz}=\dfrac{\dfrac{16}{9}t^3}{t^3}=\dfrac{16}{9} \] The velocity of the curve and its length are: \[\begin{aligned} \vec v&=(t,2t^{1/2},2) \\ |\vec v|&=\sqrt{t^2+4t+4}=\sqrt{(t+2)^2}=t+2 \\ \end{aligned}\] In general a scalar line integral is: \[ \int_A^B f\,ds=\int_a^b f(\vec r(t))|\vec v|\,dt \] In this case it is: \[\begin{aligned} \int_{\vec r(1)}^{\vec r(3)} &\dfrac{y^2}{xz}\,ds =\int_1^3 \dfrac{16}{9}(t+2)\,dt \\ &=\dfrac{16}{9}\left[\dfrac{t^2}{2}+2t\right]_1^3 \\ &=\dfrac{16}{9}\left(\dfrac{9}{2}+6-\dfrac{1}{2}-2\right) =\dfrac{128}{9} \end{aligned}\]

as,py
Compute \(\displaystyle \int xyz\,ds\) along the curve \(r(t)=(3t,4t,5t)\) from the point \((0,0,0)\) to the point \((6,8,10)\).

\(\displaystyle \int_{(0,0,0)}^{(6,8,10)} xyz\,ds =1200\sqrt{2}\)

At the endpoints, the values of \(t\) are \(t=0\) and \(t=2\). The velocity is \(v=(3,4,5)\) and its length is: \[ |v|=\sqrt{9+16+25}=\sqrt{50}=5\sqrt{2} \] The integral becomes: \[\begin{aligned} \int_{(0,0,0)}^{(6,8,10)} &xyz\,ds =\int_0^2 (3t\cdot4t\cdot5t)|v|\,dt \\ &=\int_0^2 60t^3 5\sqrt{2}\,dt =300\sqrt{2}\left[\dfrac{t^4}{4}\right]_0^2 \\ &=300\sqrt{2}\,(4)=1200\sqrt{2} \end{aligned}\]

as,py

Compute \(\displaystyle \int_A^B xy\,ds\) along the helix \(\vec r(\theta)=(4\cos \theta,4\sin \theta,3\theta)\) between \(A=\left(2\sqrt{3},2,\dfrac{\pi}{2}\right)\) and \(B=\left(2,2\sqrt{3},\pi\right)\).

What is an antiderivative of \(\sin\theta\cos\theta\)?

\(\displaystyle \int_{(2\sqrt{3},\,2,\,\pi/2)}^{(2,\,2\sqrt{3},\,\pi)} xy\,ds=20\)

At the endpoints, the values of \(\theta\) are \(\theta=\pi/6\) and \(\theta=\pi/3\). The velocity and its length are: \[\begin{aligned} \vec v&=(-4\sin\theta,\,4\cos\theta,\,3) \\ |\vec{v}|&=\sqrt{(-4\sin\theta)^2+(4\cos\theta)^2+3^2}=\sqrt{25}=5 \end{aligned}\] The integral becomes: \[\begin{aligned} &\int_{(2\sqrt{3},\,2,\,\pi/2)}^{(2,\,2\sqrt{3},\,\pi)} xy\,ds =\int_{\pi/6}^{\pi/3} xy\,|\vec{v}|\,d\theta \\ &\quad=\int_{\pi/6}^{\pi/3}(4\cos\theta)(4\sin\theta)(5)\,d\theta =80\int_{\pi/6}^{\pi/3}\cos\theta\sin\theta\,d\theta \\ &\quad=80\left[\dfrac{\sin^2\theta}{2}\right]_{\pi/6}^{\pi/3} =40\left(\dfrac{3}{4}-\dfrac{1}{4}\right) =20 \end{aligned}\]

pt

Compute \(\displaystyle \int_{(-3,9,-18)}^{(3,9,18)} \left(y+\dfrac{3z}{x}\right)\,ds\) along the twisted cubic \(\vec r(t)=\left(t,t^2,\dfrac{2}{3}t^3\right)\).

What are the values of \(t\) at the \(2\) endpoints?

\(\displaystyle \int_{(-3,\,9,\,-18)}^{(3,\,9,\,18)}\left(y+\dfrac{3z}{x}\right)\,ds=\dfrac{3186}{5}\)

At the endpoints, the values of \(t\) are \(t=-3\) and \(t=3\). The velocity is \(\vec{v}(t)=(1,\,2t,\,2t^2)\) and its length is: \[ |\vec{v}|=\sqrt{1^2+(2t)^2+(2t^2)^2}=\sqrt{4t^4+4t^2+1}=2t^2+1 \] The integral becomes: \[\begin{aligned} \int_{(-3,\,9,\,-18)}^{(3,\,9,\,18)}&\left(y+\dfrac{3z}{x}\right)\,ds =\int_{-3}^{3}\left(t^2+3\dfrac{2t^3}{3t}\right)|\vec{v}|\,dt \\ &=\int_{-3}^{3}3t^2(2t^2+1)\,dt =3\left[\dfrac{2}{5}t^5+\dfrac{1}{3}t^3\right]_{-3}^{3} \\ &=6\left(\dfrac{2}{5}3^5+\dfrac{1}{3}3^3\right) =\dfrac{3186}{5} \end{aligned}\]

pt

c. Applications of Scalar Line Integrals

Note: In the problems with a density function, the plots use a darker colors where it is more dense.

Consider the function \(f(x,y,z)=xy\) along the helix \(\vec r(\theta)=(4\cos \theta,4\sin \theta,3\theta)\) between \(A=\left(2\sqrt{3},2,\dfrac{\pi}{2}\right)\) and \(B=\left(2,2\sqrt{3},\pi\right)\).
1. Find the average value of the function, \(f\), along the helix.
  See two previous problems, here and here.
  
  The length was computed here and the integral of \(f\) was computed here.
  
  \(f_{\text{ave}}=\dfrac{24}{\pi}\)
  
  The average value of \(f\) along the path is given by the expression: \[ f_{\text{ave}}=\dfrac{1}{L}\int_{A}^{B}f(x,\,y,\,z)\,ds \] We computed the arclength \(L=\dfrac{5\pi}{6}\) in a previous problem, and we computed the value of the integral \[ \int_A^B xy\,ds=20 \] in another problem. This gives us the following: \[ f_{\text{ave}}=\dfrac{6}{5\pi}\left(20\right)=\dfrac{24}{\pi} \]
  
  pt
2. Find the weighted average of the function, \(f\), along the helix if the weight factor is \(\delta=z\).
  
  Use the identity \(\sin\theta\cos\theta=\dfrac{1}{2}\sin(2\theta)\) and then integrate by parts.
  
  \(f_{\delta\text{-ave}}=\dfrac{24}{\pi}\)
  
  The weighted average value of \(f\) along the path is given by the expression: \[ f_{\delta\text{-ave}}=\dfrac{\int_A^B\delta f(x,\,y,\,z)\,ds} {\int_A^B \delta\,ds} \] We recall that \(|v|=5\) and \(z=3\theta\). So the denominator is: \[\begin{aligned} \int_A^B \delta\,ds &=\int_A^B z|\vec v|\,d\theta =\int_{\pi/6}^{\pi/3}3\theta\cdot5\,d\theta \\ &=15\left[\frac{\theta^2}{2}\right]_{\pi/6}^{\pi/3} =\frac{15\pi^2}{2}\left(\dfrac{1}{9}-\dfrac{1}{36}\right) =\frac{5\pi^2}{8} \end{aligned}\] We now compute the value of the numerator, using the formula \(\sin\theta\cos\theta=\dfrac{1}{2}\sin(2\theta)\): \[\begin{aligned} \int_A^B\delta f\,ds&=\int_{\pi/6}^{\pi/3} z\cdot xy\cdot5\,d\theta \\ \qquad&=5\int_{\pi/6}^{\pi/3}(3\theta)(4\cos\theta)(4\sin\theta)\,d\theta \\ \qquad&=120\int_{\pi/6}^{\pi/3}\theta\sin(2\theta)\,d\theta \end{aligned}\] Now we use integration by parts with \[\begin{array}{ll} u=\theta & dv=\sin(2\theta)d\theta \\ du=d\theta \quad & v=-\,\dfrac{\cos(2\theta)}{2} \end{array}\] Our integral becomes: \[\begin{aligned} \int_A^B\delta f\,ds &=120\left[-\,\dfrac{\theta\cos(2\theta)}{2}+\dfrac{1}{2}\int \cos(2\theta)\,d\theta\right]_{\pi/6}^{\pi/3} \\ \qquad&=120\left[-\,\dfrac{\theta\cos(2\theta)}{2}+\dfrac{1}{2}\dfrac{\sin(2\theta)}{2}\right]_{\pi/6}^{\pi/3} \\ \qquad&=120\left(\dfrac{\pi}{12}+\dfrac{\sqrt{3}}{8}\right) -120\left(-\,\dfrac{\pi}{24}+\dfrac{\sqrt{3}}{8}\right) \\ \qquad&=120\left(\dfrac{\pi}{8}\right)=15\pi \end{aligned}\] Thus, the weighted average is: \[ f_{\delta\text{-ave}}=\dfrac{8(15\pi)}{5\pi^2}=\dfrac{24}{\pi} \]
  
  pt

Consider the function \(f(x,y,z)=y+\dfrac{3z}{x}\) along the twisted cubic \(r(t)=\left(t,t^2,\dfrac{2}{3}t^3\right)\) between the points \(A=(-3,9,-18)\) and \(B=(3,9,18)\).
1. Find the average value of the function, \(f\), along the curve.
  See two previous problems, here and here.
  
  The length was computed here and the integral of \(f\) was computed here.
  
  \(f_\text{ave}=\dfrac{531}{35}\)
  
  The average value of \(f\) along the path is given by the expression: \[ f_{\text{ave}}=\dfrac{1}{L}\int_{A}^{B}f(x,\,y,\,z)\,ds \] We computed the value \(L=42\) in a previous problem, and we computed the numerator \(\displaystyle \int_{A}^{B}f\,ds=\dfrac{3186}{5}\) in another problem. This gives us the following: \[ f_{\text{ave}}=\dfrac{1}{42}\left(\dfrac{3186}{5}\right)=\dfrac{531}{35} \]
  
  pt
2. Find the weighted average of the function, \(f\), along the curve if the weight factor is \(\delta=y\).
  
  \(\displaystyle f_{\delta\text{-ave}}=\dfrac{7857}{413}\)
  
  The weighted average value of \(f\) along the path is give n by the expression: \[ f_{\delta\text{-ave}}=\frac{\int_A^B\delta f(x,\,y,\,z)\,ds}{\int_A^B\delta\,ds} \] We recall that \(|\vec{v}|=2t^2+1\) and \(y=t^2\). So the denominator is: \[\begin{aligned} \int_A^B\delta\,ds &=\int_A^By|\vec{v}|\,dt =\int_{-3}^3t^2(2t^2+1)\,dt \\ &=\left[\frac{2t^5}{5}+\frac{t^3}{3}\right]_{-3}^3 =2\left(\frac{2}{5}243+9\right) =\frac{1062}{5} \end{aligned}\] We now compute the numerator. We note: \[ f=y+\dfrac{3z}{x}=t^2+\dfrac{2t^3}{t}=3t^2 \] So: \[\begin{aligned} \int_A^B\delta f\,ds&=\int_{-3}^3t^2(3t^2)(2t^2+1)\,dt =3\int_{-3}^32t^6+t^4\,dt \\ &=3\left[\frac{2t^7}{7}+\frac{t^5}{5}\right]_{-3}^3 =6\left(\frac{2}{7}3^7+\frac{1}{5}3^5\right) \\ &=6\cdot243\left(\frac{2}{7}9+\frac{1}{5}\right) =\frac{141426}{35} \end{aligned}\] Thus, the weighted average is: \[ f_{\delta\text{-ave}}=\dfrac{141426}{35}\dfrac{5)}{1062}=\dfrac{7857}{413} \]
  
  pt
A wire has the shape of the helix \(\vec r(\theta)=(4\cos \theta,4\sin \theta,3\theta)\) between \(A=\left(2\sqrt{3},2,\dfrac{\pi}{2}\right)\) and \(B=\left(2,2\sqrt{3},\pi\right)\) and has mass density \(\delta=z\).
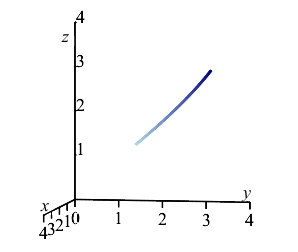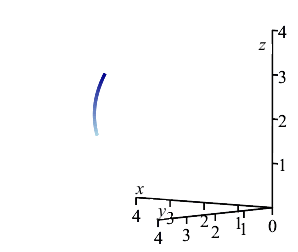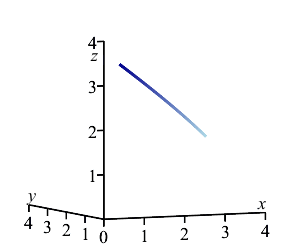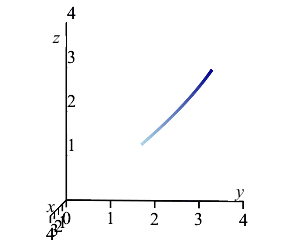
1. Find the total mass.
  
  \(\displaystyle M=\int_A^B\delta\,ds=\int_a^b \delta|\vec v|\,d\theta\)
  
  \(\displaystyle M=\dfrac{5\pi^2}{8}\)
  
  We recall the formula for mass: \[ M=\int_A^B\delta\,ds=\int_{\pi/6}^{\pi/3} \delta|\vec v|\,d\theta \] Since \(|v|=5\) and \(\delta=z=3\theta\) the mass is: \[\begin{aligned} M&=\int_{\pi/6}^{\pi/3}3\theta\cdot5\,d\theta \\ &=15\left[\frac{\theta^2}{2}\right]_{\pi/6}^{\pi/3} =\frac{15\pi^2}{2}\left(\dfrac{1}{9}-\dfrac{1}{36}\right) =\frac{5\pi^2}{8} \end{aligned}\]
  
  pt
2. Find the \(z\)-component of the center of mass.
  
  \(\displaystyle \bar z=\dfrac{M_z}{M}\) where \(\displaystyle M_z=\int_{A}^{B}z\delta\,ds=\int_a^bz\delta|\vec v|\,d\theta \)
  
  \(\displaystyle \bar z=\dfrac{M_z}{M}=\dfrac{7\pi}{9}\)
  
  The first moment of mass in the \(z\) direction is: \[\begin{aligned} M_z&=\int_{A}^{B}z\delta\,ds=\int_{\pi/6}^{\pi/3}(3\theta)(3\theta)(5)\,d\theta =45\int_{\pi/6}^{\pi/3}\theta^2\,d\theta \\ &=45\left[\dfrac{\theta^3}{3}\right]_{\pi/6}^{\pi/3}=15\pi^3\left(\dfrac{1}{27}-\dfrac{1}{216}\right)=\dfrac{35\pi^3}{72} \end{aligned}\] So the \(z\) component of the center of mass is: \[ \bar z=\dfrac{M_z}{M} =\dfrac{35\pi^3}{72}\dfrac{8}{5\pi^2}=\dfrac{7\pi}{9} \]
  
  The plot on the right shows the center of mass in relation to the curve between the points \(A\) and \(B\). Note that the center of mass does not lie on the curve; instead, it lies off the curve on the side that it is bending toward.
  
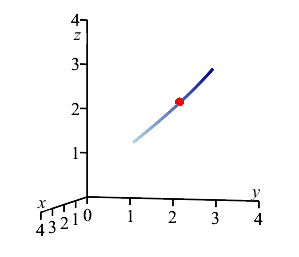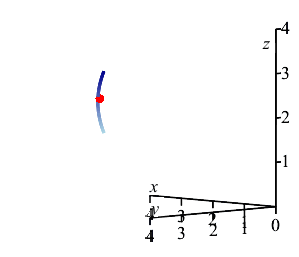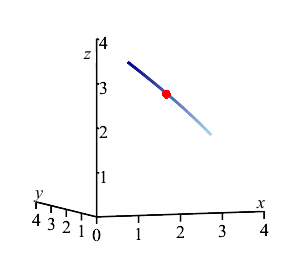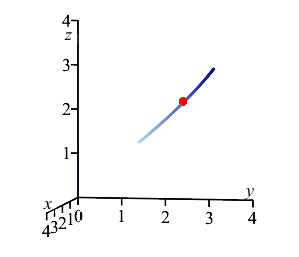
  pt
A wire has the shape of the twisted cubic \(r(t)=\left(t,t^2,\dfrac{2}{3}t^3\right)\) between the points \(A=(-3,9,-18)\) and \(B=(3,9,18)\) and has mass density \(\delta=y\).
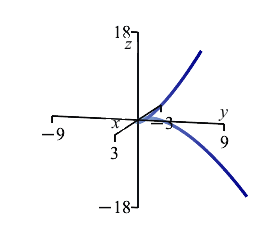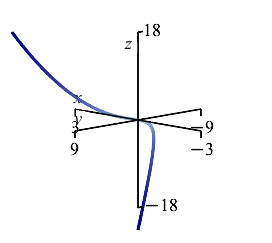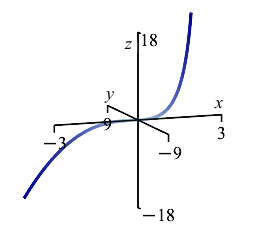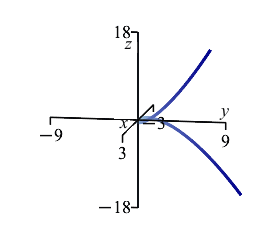
1. Find the total mass.
  
  \(\displaystyle M=\int_A^B\delta\,ds=\int_a^b \delta|\vec v|\,d\theta\)
  
  \(\displaystyle M=\dfrac{1062}{5}=212.4\)
  
  We recall the formula for mass: \[ M=\int_A^B\delta\,ds=\int_{-3}^3\delta|\vec{v}|\,dt \] Since \(\delta=y=t^2\) and \(|\vec v|=2t^2+1\), the mass is: \[\begin{aligned} M&=\int_{-3}^3t^2(2t^2+1)\,dt \\ &=\left[\frac{2t^5}{5}+\frac{t^3}{3}\right]_{-3}^3 =2\left(\frac{2}{5}243+9\right) =\frac{1062}{5}=212.4 \end{aligned}\]
  
  pt
2. Find the \(y\)-component of the center of mass.
  
  \(\displaystyle \bar y=\dfrac{M_y}{M}\) where \(\displaystyle M_y=\int_{A}^{B}y\delta\,ds=\int_a^by\delta|\vec v|\,d\theta \)
  
  \(\displaystyle \bar y=\dfrac{M_y}{M} =\dfrac{2619}{413} \approx6.34\)
  
  Since \(y=t^2\) and \(\delta=y=t^2\), the first moment of mass in the \(y\) direction is: \[\begin{aligned} M_y&=\int_{A}^{B}y\delta\,ds=\int_{-3}^{3}t^4(2t^2+1)\,dt \\ &=\left[\dfrac{2t^7}{7}+\dfrac{t^5}{5}\right]_{-3}^{3} =2\left(\dfrac{2\cdot3^7}{7}+\dfrac{3^5}{5}\right) \\ &=2\cdot3^5\left(\dfrac{18}{7}+\dfrac{1}{5}\right) =2\cdot3^5\dfrac{97}{35}\approx1346.9 \end{aligned}\] So the \(y\) component of the center of mass is: \[ \bar y=\dfrac{M_y}{M}=2\cdot3^5\dfrac{97}{35}\dfrac{5}{1062} =\dfrac{2619}{413} \approx6.34 \]
  
  The plot on the right shows the center of mass in relation to the curve between the points \(A\) and \(B\).
  Notice that \(\bar x=\bar z=0\) by symmetry.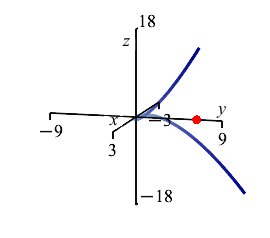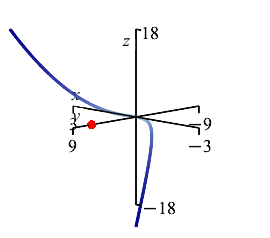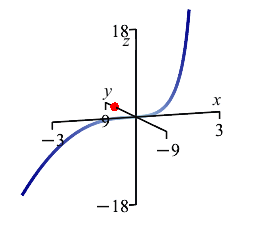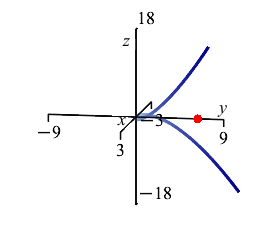
  
  pt
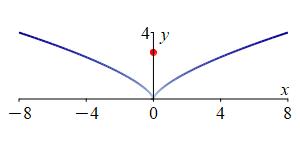
Find the mass and center of mass of the cusp \(y^3=x^2\) for \(-8 \le x \le 8\) if the linear density is \(\delta=y\). The cusp may be parametrized as \(\vec r(t)=(t^3,t^2)\) from \(t=-2\) to \(t=2\).

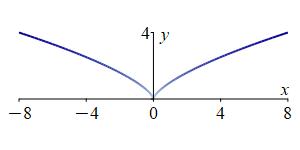
\(M=\dfrac{128}{1215}\left(1+125\sqrt{10}\right) \approx41.7\)
\((\bar{x},\bar{y})\approx(0,2.82)\)

The velocity is \(\vec v=\langle 3t^2,2t\rangle\) and its magnitude is \(|\vec v|=\sqrt{9t^4+4t^2}=|t|\sqrt{9t^2+4}\). Notice that when we factor a \(t^2\) out of the square root it becomes \(|t|\) because the radical means the positive square root. The density on the curve is \(\delta=y=t^2\). So the mass is \[ M=\int_A^B \delta\,ds=\int_{-2}^2 t^2\cdot |t|\sqrt{9t^2+4}\,dt \] Since the integrand is an even function, we can double half the integral: \[ M=2\int_0^2 t^2\cdot t\sqrt{9t^2+4}\,dt \] To do the integral, we use the substitution \(u=9t^2+4\). So \(du=18t\,dt\) and \(t^2=\dfrac{u-4}{9}\): \[\begin{aligned} M&=\dfrac{1}{9}\int_4^{40} \dfrac{u-4}{9}\sqrt{u}\,du =\dfrac{1}{81}\left[\dfrac{2u^{5/2}}{5}-4\dfrac{2u^{3/2}}{3}\right]_4^{40} \\ &=\cdots =\dfrac{128}{1215}\left(1+125\sqrt{10}\right) \approx41.7 \end{aligned}\] For the \(x\) moment, we add a factor of \(x=t^3\) in the integrand: \[ M_x=\int_A^B x\,ds=\int_{-2}^2 t^3\cdot t^2\cdot |t|\sqrt{9t^2+4}\,dt \] Since the integrand is an odd function, the integral is \(0\): \[ M_x=0 \] For the \(y\) moment, we insert \(y=t^2\): \[ M_y=\int_A^B y\,ds=\int_{-2}^2 t^2\cdot t^2\cdot |t|\sqrt{9t^2+4}\,dt \] Since the integrand is an even function, we can double half the integral: \[ M_y=2\int_0^2 t^5\sqrt{9t^2+4}\,dt \] We again use the substitution \(u=9t^2+4\) with \(du=18t\,dt\) and \(t^2=\dfrac{u-4}{9}\): \[\begin{aligned} M_y&=\dfrac{1}{9}\int_4^{40} \left(\dfrac{u-4}{9}\right)^2\sqrt{u}\,du \\ &=\dfrac{1}{9^3}\int_4^{40} (u^2-8u+16)\sqrt{u}\,du \\ &=\dfrac{1}{9^3}\left[\dfrac{2}{7}u^{7/2}-\dfrac{16}{5}u^{5/2}+\dfrac{32}{3}u^{3/2}\right]_4^{40} \\ &=\cdots =\dfrac{570\,880}{15\,309}\sqrt{10}-\dfrac{2048}{76545} \approx117.9 \end{aligned}\] We now divide each moment by the mass to get the center of mass: \[\begin{aligned} \bar{x}=\dfrac{M_x}{M}&=0 \\ \bar{y}=\dfrac{M_y}{M}&=\dfrac{117.9}{41.7} =2.82 \end{aligned}\] So the center of mass is at: \[ (\bar{x},\bar{y})=(0,2.82) \] This is reasonable because the curve and density are symmetric on left and right and \(0 \le \bar y \le 4\).

The plot on the right shows the center of mass of the curve as a red circle.

pt,tj
Consider a piece of wire bent into a curve shaped like the exponential function \(y=e^x\) on the interval \(0 \lt x \lt \ln2\) with a linear density given by \(\delta(x,\,y)=y^2\). Find the total mass of the wire.

\(\displaystyle M=\dfrac{1}{3}\left(5^{3/2}-2^{3/2}\right)\approx2.78\)

The mass is: \[ M=\int_a^b \delta(r(t))|\vec v|\,dt\] Since \(\vec r(t)=(t,e^t)\), we compute \(\vec v(t)=(1,e^t)\) and \(|\vec v(t)|=\sqrt{1+e^{2t}}\). Additionally, The density is \(\delta(x,\,y)=y^2=e^{2t}\). Thus the mass integral becomes: \[ M=\int_0^{\ln2} e^{2t}\sqrt{1+e^{2t}}\,dt \] To do the integral, we use the substitution \(u=1+e^{2t}\) and \(du=2e^{2t}\). So: \[\begin{aligned} M&=\dfrac{1}{2}\int_2^5\sqrt{u}\,du =\dfrac{1}{3}\left[u^{3/2}\right]_2^5 \\ &=\dfrac{1}{3}\left(5^{3/2}-2^{3/2}\right) \approx2.78 \end{aligned}\]

as, pt
Consider a piece of wire in the shape of the parabola \(y=\dfrac{2}{3}x^2\) on the interval \(\dfrac{3}{4} \lt x \lt 1\) and a linear density given by \(\delta(x,y)=x\).
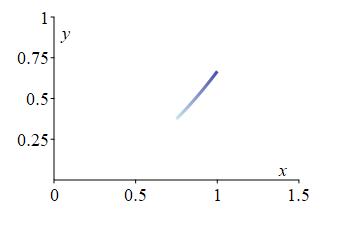
1. Find the total mass of the wire.
  
  The total mass is given by \[ M=\int_a^b \delta(r(t))|\vec v|\,dt \]
  
  \(\displaystyle M =\dfrac{3}{16}\left(\dfrac{125}{27}-2\sqrt{2}\right)\approx.338\)
  
  Recall that the total mass is given by the formula: \[M=\int_a^b \delta(r(t))|\vec v|\,dt\] Since \(r(t)=\left(t,\dfrac{2}{3}t^2\right)\), we know that \(v(t)=\left(1,\dfrac{4}{3}t\right)\) and \(|v(t)|=\sqrt{1+\dfrac{16}{9}t^2}\). Additionally since \(\delta(x,y)=x\) it follows that \(\delta(t)=t\). Thus our integral becomes: \[ M=\int_{3/4}^1 t\sqrt{1+\dfrac{16}{9}t^2}\,dt \] We make the substitution \(u=1+\dfrac{16}{9}t^2\). So \(du=\dfrac{32}{9}t\,dt\) and \(\dfrac{9}{32}\,du=t\,dt\). The integral becomes: \[\begin{aligned} M&=\dfrac{9}{32}\int_2^{25/9}\sqrt{u}\,du \\ &=\dfrac{9}{32}\left[\dfrac{2u^{3/2}}{3}\right]_2^{25/9} =\dfrac{3}{16}\left(\dfrac{125}{27}-2\sqrt{2}\right)\approx.338 \end{aligned}\]
  
  pt
2. Find the \(y\)-component of the center of mass.
  
  The \(y\)-component of the center of mass is \[ \bar y=\dfrac{M_y}{M} \] where \[ M=\int_a^b \delta(r(t))|\vec v|\,dt \quad \text{and} \quad M_y=\int_a^b y\delta(r(t))|\vec v|\,dt \]
  
  \(M_y=\dfrac{125}{576}-\dfrac{9}{320}\sqrt{2}\approx.1772\)
  \(\bar y\approx.524\)
  
  We recall the formula for the \(y\) moment: \[ M_y=\int y\delta\,ds \] Substituting our known values this integral becomes: \[ M_y=\dfrac{2}{3}\int_{3/4}^1 t^3\sqrt{1+\dfrac{16}{9}t^2}\,dt \] We make the substitution \(u=1+\dfrac{16}{9}t^2\). Then \(\dfrac{9}{32}\,du=t\,dt\) and \(\dfrac{9}{16}(u-1)=t^2\). The integral becomes: \[\begin{aligned} M_y&=\dfrac{2}{3}\dfrac{9}{32}\dfrac{9}{16}\int_2^{25/9}\left(u^{3/2}-u^{1/2}\right)\,du =\dfrac{27}{256}\left[\dfrac{2u^{5/2}}{5}-\dfrac{2u^{3/2}}{3}\right]_2^{25/9} \\ &=\dfrac{27}{256}\left[\left(\dfrac{1250}{243}-\dfrac{250}{81}\right) -\left(\dfrac{8\sqrt{2}}{5}-\dfrac{4\sqrt{2}}{3}\right)\right] \\ &=\dfrac{125}{576}-\dfrac{9}{320}\sqrt{2}\approx.1772 \end{aligned}\] So the \(y\) component of the center of mass is: \[ \bar y=\dfrac{M_y}{M}\approx\dfrac{.1772}{.338}=.524 \]
  
  The plot on the right shows the center of mass of the curve as a red point. While it may appear that the center of mass is on the curve, it is actually slightly off to the left, in the direction that the curve is bending.
  
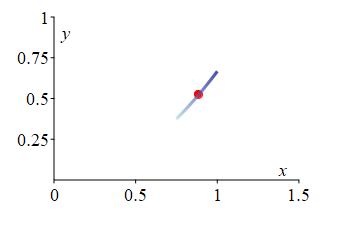
  pt

d. Line Integrals of Vectors

Compute \(\displaystyle \int_{(3,3,2)}^{(6,12,16)} \vec F\cdot d\vec s\) along the twisted cubic \(\vec r(t)=(3t,3t^2,2t^3)\) for the vector field \(\vec F=(y^2,2z,x^2)\).

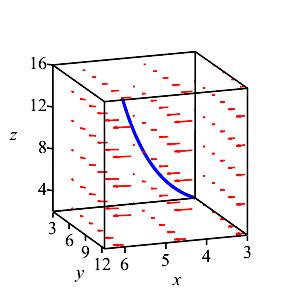
First find \(F(\vec r(t))\) and \(d\vec s=\vec v\,dt\) in terms of t. Then integrate their dot product between the values of \(t\) that correspond to the points on the curve for the limits.

\(\displaystyle \int_{(3,3,2)}^{(6,12,16)} \vec F\cdot d\vec s=\dfrac{2628}{5}\)

Note that \((3,\,3,\,2)=(3t,\,3t^2,\,2t^3)\) when \(t=1\) and \((6,\,12,\,16)=(3t,\,3t^2,\,2t^3)\) when \(t=2\). Thus, our integral becomes: \[\int_{(3,3,2)}^{(6,12,16)} \vec F\cdot d\vec s=\int_1^2\vec{F}\left(\vec{r}(t)\right)\cdot\vec{v}(t)\,dt\] We plug in: \(\vec F(\vec r(t))=(6t^2,4t^3,9t^2)\) and \(d\vec s=\vec v\,dt=(3,6t,6t^2)\,dt\). Thus: \[\begin{aligned} \int_{(3,3,2)}^{(6,12,16)} &\vec F\cdot d\vec s =\int_1^2 (18t^2+78t^4)\,dt =\left[6t^3+\dfrac{78t^5}{5}\right]_1^2 \\ &=\left(48+\dfrac{78\cdot32}{5}\right)-\left(6+\dfrac{78}{5}\right) =\dfrac{2628}{5} \end{aligned}\]

as, pt
Compute \(\displaystyle \int_{(0,0,0)}^{(2,4,8)} \vec F\cdot d\vec s\) along the twisted cubic \(\vec r(t)=(t,t^2,t^3)\) for the vector field \(\vec F=(yz,xz,xy)\).

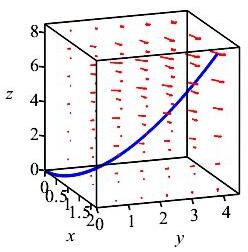
\(\displaystyle \int_{(0,0,0)}^{(2,4,8)} \vec F\cdot d\vec s =64\)

Note that \((0,\,0,\,0)=(t,\,t^2,\,t^3)\) when \(t=0\) and \((2,\,4,\,8)=(t,\,t^2,\,t^3)\) when \(t=2\). Thus, our integral becomes: \[ \int_{(0,0,0)}^{(2,4,8)}\vec F\cdot d\vec s =\int_0^2\vec{F}\left(\vec{r}(t)\right)\cdot\vec{v}(t)\,dt \] Plugging in: \(\vec F(\vec r(t))=(t^5,t^4,t^3)\) and \(d\vec s=\vec v\,dt=(1,2t,3t^2)\,dt\). Thus: \[\begin{aligned} \int_{(0,0,0)}^{(2,\,4,\,8)} &\vec F \cdot d\vec s =\int_0^2 6t^5\,dt \\ &=\left[\rule{0pt}{10pt}t^6\right]_0^2=2^6=64 \end{aligned}\]

as, pt
Compute \(\displaystyle \int_{(0,1,0)}^{(0,-1,\pi^2)} 2ydx-2xdy+zdz\) along the curve \(\vec r(t)=(\sin t,\cos t,t^2)\).

\(\displaystyle \int_{(0,1,0)}^{(0,-1,\pi^2)} 2ydx+2xdy+zdz =2\pi+\dfrac{\pi^4}{2}\)

Note that \((0,1,0)=(\sin t,\cos t,t^2)\) when \(t=0\) and \((0,-1,\pi^2)=(\sin t,\cos t,t^2)\) when \(t=\pi\). Furthermore, since \[ x=\sin t \qquad y=\cos t \qquad z=t^2 \] we compute \[ dx=\cos t\,dt \qquad dy=-\sin t\,dt \qquad dz=2t\,dt \] Thus: \[\begin{aligned} \int_{(0,1,0)}^{(0,-1,\pi^2)} 2ydx-2xdy+zdz &=\int_0^\pi \left(2\cos^2t+2\sin^2t+2t^3\right)\,dt \\ =\int_0^\pi \left(2+2t^3\right)\,dt &=\left[2t+\dfrac{t^4}{2}\right]_0^\pi =2\pi+\dfrac{\pi^4}{2} \end{aligned}\]

as, pt

e. Applications of Vector Line Integrals

Find the work done by the force \(\vec F=(y^2+z,x^2+z,x+y)\) on an object which moves it along the curve defined by \(\vec r(t)=(t,2t,3t^2)\) from \((-1,-2,3)\) to \((3,6,27)\).

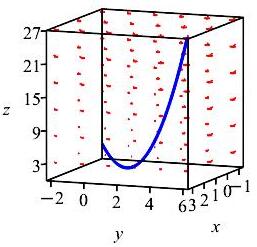
\(\displaystyle W=\int_A^B \vec F\cdot d\vec s\)

\(\displaystyle W=\int_{(-1,-2,3)}^{(3,6,27)}\vec F\cdot d\vec s=308\)

Note that \((-1,-2,3)=(t,2t,3t^2)\) when \(t=-1\) and \((3,6,27)=(t,2t,3t^2)\) when \(t=3\). Thus our integral becomes: \[ W=\int_{(-1,-2,3)}^{(3,6,27)}\vec F\cdot d\vec s =\int_{-1}^3 \vec{F}\left(\vec{r}(t)\right)\cdot\vec{v}(t)\,dt \] We plug in: \(\vec{F}\left(\vec{r}(t)\right)=\left(7t^2,4t^2,3t\right)\) and \(d\vec{s}=\vec{v}dt=(1,2,6t)\,dt\). Thus: \[\begin{aligned} \int_{(-1,-2,3)}^{(3,6,27)} \vec F\cdot d\vec{s} &=\int_{-1}^3\left(7t^2+8t^2+18t^2\right)\,dt \\ =\int_{-1}^3 33t^2\,dt &=\left[11t^3\right]_{-1}^3=11(27--1) =308 \end{aligned}\]

as,pt
Find the flow of the velocity field \(\vec V=(yz,xz,xy)\) along the curve \(\vec r(t)=(t+1,-4t^2,t^3)\) from \((1,0,0)\) to \((3,-16,8)\). Is the fluid flowing in the same or opposite direction as the curve is traversed?

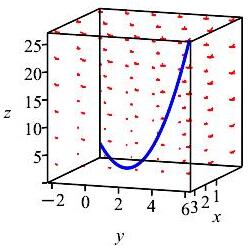
Be sure to distinguish between the velocity field \(\vec V=(yz,xz,xy)\) and the tangent vector to the curve \(\vec v=\dfrac{dr}{dt}\).

\(\text{Flow}\,=-384\) The fluid is flowing opposite to the direction of the curve.

The flow is given by the formula: \[ \text{Flow}\,=\int_A^B\vec V\cdot d\vec s \] Since \(\vec r(t)=(t+1,-4t^2,t^3)\), we note that \(\vec r(t)=(1,0,0)\) when \(t=0\) and \(\vec r(t)=(3,-16,8)\) when \(t=2\). Substituting for \(x,y,\) and \(z\) in \(\vec V=(yz,xz,xy)\), we find: \[ V=(-4t^5,t^4+t^3,-4t^3-4t^2) \] The differential of arclength is \(d\vec s=\vec v\,dt=(1,-8t,3t^2)\,dt\). So: \[\begin{aligned} \vec V\cdot d\vec s&=(-4t^5-8t^5-8t^4-12t^5-12t^4)\,dt \\ &=-(24t^5+20t^4)\,dt \end{aligned}\] Plugging this into the flow integral gives: \[\begin{aligned} \int_{(1,0,0)}^{(3,-16,8)} \vec V\cdot d\vec s &=\int_0^2 -(24t^5+20t^4)\,dt \\ &=-[4t^6+4t^5]_0^2=-384. \end{aligned}\] Since the flow is negative, the fluid is flowing opposite to the direction of the curve.

as,pt,tj

Find the circulation of the velocity field \(\vec V=(-x^2y,x^3)\) counterclockwise around the circle \(x^2+y^2=9\).

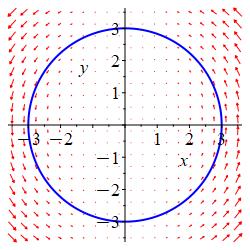
Be sure to distinguish between the velocity field \(\vec V=(yz,xz,xy)\) and the tangent vector to the curve \(\vec v=\dfrac{dr}{dt}\).

\(\text{Circulation}\,=81\pi\)

We can parametrize the circle \(x^2+y^2=9\) counterclockwise as: \[ \vec r(t)=(3\cos t,3\sin t) \] Note that \(0\leq t\lt 2\pi\). We substitute \(x\) and \(y\) into \(\vec V=(-x^2y,x^3)\): \[ \vec V=(-27\cos^2 t\sin t,27\cos^3 t) \] The tangent vector to the curve is \(\vec v=(-3\sin t,3\cos t)\). So \[ \vec V\cdot \vec v=81\cos^2 t\sin^2 t+81\cos^4 t=81\cos^2 t \] The circulation is. \[\begin{aligned} \text{Circulation}\,&=\oint_{\vec r} \vec V\cdot d\vec s =\int_0^{2\pi} \vec V\cdot\vec v\,dt \\ &=\int_0^{2\pi} 81\cos^2 t\,dt =\dfrac{81}{2}\int_0^{2\pi}(1+\cos(2t))\,dt \\ &=\dfrac{81}{2}\left[t+\dfrac{\sin2t}{2}\right]_0^{2\pi} =81\pi \end{aligned}\]

pt

Find the circulation of the magnetic field \(\vec B=(-y^3,xy^2,0)\) counterclockwise around the parabola \(y=x^2\) and the line segment \(y=4\), both in the \(xy\)-plane.

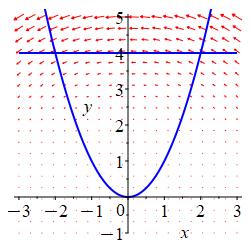
The parabola may be parametrized as \(\vec r=(t,t^2,0)\).
The line segment may be parametrized as \(\vec r=(-t,4,0)\). Notice that as \(t\) increases, we move leftward on the line segment.

\(\displaystyle \text{Circulation}=\oint_{\vec r} \vec B\cdot d\vec s =\dfrac{2^{11}}{7}\)

To parametrize the parabola \(y=x^2\) counterclockwise, we need to go left to right. So is parametrization is: \[ \vec r_P(t)=(t,t^2,0) \quad \text{with} -2\le t\le 2 \] The tangent vector is: \[ \vec v_P(t)=(1,2t,0) \] which does point to the right. We substitute \(\vec r_P\) into \(\vec B=(-y^3,xy^2,0)\): \[ \vec B_P=(-t^6,t^5,0) \] So \(\vec B_P\cdot \vec v_P=t^6\) and the flow along the parabola is: \[\begin{aligned} \text{Flow}_P\,&=\int_P \vec B\cdot d\vec s =\int_{-2}^2\vec B_P\cdot \vec v_P\,dt \\ &=\int_{-2}^2 t^6\,dt =\left[\dfrac{t^7}{7}\right]_{-2}^2 =\dfrac{2^8}{7} \end{aligned}\] To parametrize the line \(y=4\) counterclockwise, we need to go right to left. So is parametrization is: \[ \vec r_L(t)=(-t,4,0) \quad \text{with} -2\le t\le 2 \] The tangent vector is: \[ \vec v_L(t)=(-1,0,0) \] which does point to the left. We substitute \(\vec r_L\) into \(\vec B=(-y^3,xy^2,0)\): \[ \vec B_L=(-64,-16t,0) \] So \(\vec B_L\cdot \vec v_L=64\) and the flow along the line segment is: \[\begin{aligned} \text{Flow}_L\,&=\int_L \vec B\cdot d\vec s =\int_{-2}^2 \vec B_L\cdot \vec v_L\,dt \\ &=\int_{-2}^2 64\,dt =\left[\rule{0pt}{10pt}64t\right]_{-2}^2 =256=2^8 \end{aligned}\] So the total circulation is: \[\begin{aligned} \text{Circulation} &=\text{Flow}_P+\text{Flow}_L \\ \oint_{\vec r} \vec B\cdot d\vec s &=\int_P \vec B\cdot d\vec s+\int_L \vec B\cdot d\vec s \\ &=\dfrac{2^8}{7}+2^8 =\dfrac{2^{11}}{7} \end{aligned}\]

pt,tj

f. Normal Line Integrals in \(\mathbb{R}^2\) (Optional)

For each vector, \(\vec v\), find find its normal, \(\vec n=\vec v^\perp\), and the normal (non-parametric) equation of the line through the given point, \(P\), perpendicular to \(\vec n\).
1. \(\vec v=\langle3,5\rangle\) and \(P=(1,4)\).
  
  If \(\vec v=\langle a,b\rangle\) then \(\vec v^\perp=\langle b,-a\rangle\).
  The line through \(P\) perpendicular to \(\vec n\) is \(\vec n\cdot X=\vec n\cdot P\) where \(X=(x,y)\).
  
  \(\vec{n}=\langle5, -3\rangle\qquad\qquad 5x-3y=-7\)
  
  We recall that if \(\vec{v}=\langle v_1,v_2\rangle\), then \(\vec{n}=\vec{v}^\perp=\langle v_2,-v_1\rangle\). Thus, \(\vec{n}=\langle5,-3\rangle\). Furthermore, we recall that the line perpendicular to \(\vec{n}\) through \(P\) has the form \(\vec{n}\cdot X=\vec{n}\cdot P\) where \(X=\langle x,y\rangle\). So, we arrive at the equation \[5x-3y=5\cdot 1+(-3)\cdot 4=-7.\]
  
  pt
2. \(\vec v=\langle-4,2\rangle\) and \(P=(3,1)\).
  
  \(\vec{n}=\langle2,4\rangle\qquad\qquad2x+4y=10\)
  
  We recall that if \(\vec{v}=\langle v_1,v_2\rangle\), then \(\vec{n}=\vec{v}^{\perp}=\langle v_2,-v_1\rangle\). Thus, \(\vec{n}=\langle 2,4\rangle\). Furthermore, we recall that the line perpendicular to \(\vec{n}\) through \(P\) has the form \(\vec{n}\cdot X=\vec{n}\cdot P\) where \(X=\langle x,y\rangle\). So, we arrive at the equation \[2x+4y=2\cdot 3+4\cdot 1=10.\]
  
  pt
Compute \(\displaystyle \oint \vec F\cdot d\vec n\) for \(\vec F=\langle x^3,x^2y\rangle\) counterclockwise around the circle \(x^2+y^2=9\).

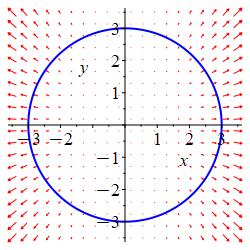
\(\vec n=\vec v^\perp\).

\(\displaystyle \oint_{\vec{r}}\vec{F}\cdot d\vec{n}=81\pi\)

We parametrize the circle \(x^2+y^2=9\) counterclockwise as: \[ \vec{r}(\theta)=(3\cos \theta,3\sin \theta) \] with \(0\leq \theta\le 2\pi\). We substitute \(x\) and \(y\) into \(F=(x^3,x^2y)\). \[ \vec{F}=(27\cos^3 \theta,27\cos^2 \theta\sin \theta) \] The tangent vector to the curve is \(\vec v=\langle-3\sin \theta,3\cos \theta\rangle\) and the normal is \(\vec{n}=(3\cos \theta,3\sin \theta)\). So \[\vec{F}\cdot\vec{n}=81\cos^4 \theta+81\cos^2\theta\sin^2 \theta=81\cos^2 \theta\] So the integral is: \[\begin{aligned} \oint_{\vec{r}}\vec{F}\cdot d\vec{n} &=\int_0^{2\pi}\vec{F}\cdot\vec{n}\,d\theta \\ &=\int_0^{2\pi}81\cos^2 \theta\,d\theta =\dfrac{81}{2}\int_0^{2\pi}(1+\cos(2\theta))\,d\theta \\ &=\dfrac{81}{2}\left[\theta+\dfrac{\sin 2\theta}{2}\right]_0^{2\pi} =81\pi \end{aligned}\]

pt

Notice that this is the same integral as in a previous problem. In that problem, we computed: \[ \oint \vec V\cdot d\vec s \quad \text{for} \quad \vec V=(-x^2y,x^3) \] In this problem, we computed: \[ \oint \vec F\cdot d\vec n \quad \text{for} \quad \vec F=(x^3,x^2y) \] They are the same because \(\vec F=\vec V^\perp\) or \(\vec V=-\vec F^\perp\).

g. Applications of Normal Line Integrals (Optional)

Find the expansion of the fluid velocity \(\vec V=\langle3x,4y\rangle\) out of the circle \(x^2+y^2=25\).

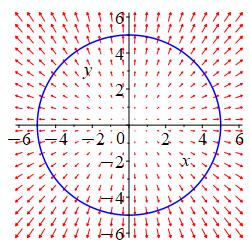
\(\displaystyle \oint_{\vec{r}}\vec{F}\cdot\,d\vec{n}=175\pi\)

We parametrize the circle \(x^2+y^2=25\) counterclockwise as: \[\vec{r}(\theta)=(5\cos\theta,5\sin\theta)\] for \(0\leq\theta\leq 2\pi\). We substitute for \(x\) and \(y\) in \(\vec V=(3x,4y)\). \[\vec V=(15\cos\theta,20\sin\theta)\] The tangent vector to the curve is \(\vec{v}=(-5\sin\theta,5\cos\theta)\) and the normal is \(\vec{n}=(5\cos\theta,5\sin\theta)\). So \[\vec V\cdot\vec{n}=75\cos^2\theta+100\sin^2\theta=75+25\sin^2\theta\] So the expansion integral is: \[\begin{aligned} \oint_{\vec{r}}\vec{F}\cdot\,d\vec{n}&=\int_0^{2\pi}\vec{F}\cdot\vec{n}\,d\theta =\int_0^{2\pi}(75+25\sin^2\theta)\,d\theta \\ &=\int_0^{2\pi} \left[75+\dfrac{25}{2}(1-\cos(2\theta))\right]\,d\theta \\ &=75\cdot2\pi+\dfrac{25}{2}\left[\theta-\dfrac{\sin(2\theta)}{2}\right]_0^{2\pi} =175\pi \end{aligned}\]

tj
Find the expansion of the fluid velocity field \(\vec V=\langle xy^2,y^3\rangle\) outward from the region bounded by the parabola \(y=x^2\) and the line segment \(y=4\).

The expansion is \(\displaystyle \oint \vec V\cdot d\vec n\).

\(\displaystyle \oint_{\vec{r}}\vec{V}\cdot d\vec{n}=\dfrac{2048}{7}\)

To compute the expansion, we need the normal to point outward, which means we must parametrize the path counterclockwise. We parametrize the parabola as: \[ \vec{r}(t)=(t,t^2) \quad \text{for} \quad -2\le t\le 2 \] To traverse the line segment from right to left, we parametrize it as: \[ \vec{r}(t)=(-t,4) \quad \text{for} \quad -2\le t\le 2 \] We substitute \(x\) and \(y\) into \(\vec V=(xy^2,y^3)\). For the parabola: \[ \vec{V}=(t^5,t^6) \] For the line: \[ \vec{V}=(-16t,64) \] We find the tangent vector, normal vector and its dot product with the fluid velocity. For the parabola: \[ \vec v=\langle1,2t\rangle \qquad \vec{n}=(2t,-1) \qquad \vec{V}\cdot\vec{n}=2t^6-t^6=t^6 \] For the line: \[ \vec v=\langle-1,0\rangle \qquad \vec{n}=(0,1) \qquad \vec{V}\cdot\vec{n}=64 \] So the integral is: \[\begin{aligned} \oint_{\vec{r}}\vec{V}\cdot d\vec{n} &=\int_{-2}^2 t^6\,dt+\int_{-2}^2 64\,dt =\left[\dfrac{t^7}{7}\right]_{-2}^2+\left[\rule{0pt}{10pt}64t\right]_{-2}^2 \\ &=\left[\dfrac{128}{7}--\,\dfrac{128}{7}\right]+[128-(-128)] \\ &=\dfrac{256}{7}+256=\dfrac{2048}{7} \end{aligned}\]

pt,tj

Notice that this is the same integral as in a previous problem. In that problem, we computed \[ \oint \vec B\cdot d\vec s \quad \text{for} \quad \vec B=(-y^3,xy^2) \] In this problem, we computed \[ \oint \vec V\cdot d\vec n \quad \text{for} \quad \vec V=(xy^2,y^3) \] They are the same because \(\vec V=\vec B^\perp\) or \(\vec B=-\vec V^\perp\).

Review Exercises

Consider a wire in the shape of the curve \(\vec r(t) =\left(2t\cos t,2t\sin t,\dfrac{1}{3}t^3\right)\). Compute each of the following. Simplify where possible.
1. The mass of the wire between \(t=0\) and \(t=1\) with linear density \(\delta=x^2+y^2\).
  
  \(M=\dfrac{52}{15}\)
  
  The velocity and its length are: \[\begin{aligned} \vec{v}&=(2\cos t-2t\sin t,2\sin(t)+2t\cos t,t^2) \\ |\vec{v}|&=\sqrt{(2\cos t-2t\sin t)^2+(2\sin t+2t\cos t)^2+(t^2)^2} \\ &=\sqrt{4+4t^2+t^4}=2+t^2 \end{aligned}\] By substitution, the density on the curve is \(\delta=x^2+y^2=4t^2\). So the mass is: \[\begin{aligned} M&=\int_{A}^{B} \delta\,ds =\int_0^1 \delta|\vec v|\,dt \\ &=\int_0^1 4t^2(2+t^2)\,dt =\int_0^1 (8t^2+4t^4)\,dt \\ &=\left[\dfrac{8t^3}{3}+\dfrac{4t^5}{5}\right]_0^1 =\dfrac{8}{3}+\dfrac{4}{5}=\dfrac{52}{15} \end{aligned}\]
  
  as,pt
2. The \(z\)-component of the center of mass of the wire between \(t=0\) and \(t=1\) with linear density \(\delta=x^2+y^2\).
  
  \(\bar{z}=\dfrac{M_{1z}}{M}\)
  where the mass is \(M\) and the \(z\)-\(1^\text{st}\) moment is
  \(\displaystyle M_{1z}=\int_a^b z(t)\delta(r(t))|\vec v|\,dt\)
  
  \(\bar{z}=\dfrac{55}{312}\approx0.176\)
  
  From the previous part, \(\delta=4t^2\) and \(|\vec v|=2+t^2\). So the \(z\) moment is: \[\begin{aligned} M_z&=\int z\delta\,ds=\int z\delta|\vec{v}|\,dt \\ &=\int_0^1 \dfrac{1}{3}t^3(4t^2)(2+t^2)\,dt =\dfrac{4}{3}\int_0^1\left(2t^5+t^7\right)\,dt \\ &=\dfrac{4}{3}\left[\dfrac{t^6}{3}+\dfrac{t^8}{8}\right]_0^1 =\dfrac{4}{3}\left(\dfrac{1}{3}+\dfrac{1}{8}\right)=\dfrac{11}{18} \end{aligned}\] Since \(M=\dfrac{52}{15}\), the \(z\) component of the center of mass is: \[\overline{z}=\dfrac{M_z}{M} =\dfrac{11}{18}\left(\dfrac{15}{52}\right) =\dfrac{55}{312}\approx 0.176\]
  
  as,pt
3. The work to move a bead along the wire from \(t=0\) to \(t=1\) if the force is \(\vec F=(-y,x,0)\)
  
  \(W=\dfrac{4}{3}\)
  
  The work is given by the integral: \[W=\int_A^B \vec{F}\cdot d\vec{s}=\int_0^1 \vec{F}\cdot\vec{v}\,dt\] On the curve, the force is \(F=(-y,x,0)=(-2t\sin t,2t\cos t,0)\) and its dot product with the tangent vector, \(\vec v=(2\cos t-2t\sin t,2\sin(t)+2t\cos t,t^2)\), is: \[\begin{aligned} \vec F\cdot\vec v &=-2t\sin t\left(2\cos t-2t\sin t\right) \\ &\quad+2t\cos t\left(2\sin t+2t\cos t\right)+0(t^2) =4t^2 \end{aligned}\] So the work is: \[ W=\int_0^1 \vec{F}\cdot\vec{v}\,dt =\int_0^1 4t^2\,dt=\left[\dfrac{4t^3}{3}\right]_0^1=\dfrac{4}{3} \]
  
  as,pt
Consider a wire in the shape of the curve \(\vec r(t)=(e^t\cos(t),e^t\sin(t),e^t)\). Compute each of the following. Simplify where possible.
1. The mass of the wire between \(t=0\) and \(t=1\) with linear density \(\delta=z\).
  
  \[ M=\int_A^B \delta\,ds \]
  
  \(M=\dfrac{\sqrt{3}}{2}(e^2-1)\approx 5.53\)
  
  The density on the curve is \(\delta(r(t))=e^t\). The velocity is: \[\begin{aligned} \vec v&=(e^t\cos(t)-e^t\sin(t),e^t\sin(t)+e^t\cos(t),e^t)\\ \end{aligned}\] The speed is: \[\begin{aligned} |\vec v(t)| &=\sqrt{(e^t\cos(t)-e^t\sin(t))^2+(e^t\sin(t)+e^t\cos(t))^2+(e^t)^2}\\ &=\sqrt{e^{2t}+e^{2t}+e^{2t}}=\sqrt{3}e^t\\ \end{aligned}\] So the mass is: \[\begin{aligned} M&=\int_{(\cos(0),\sin(0),1)}^{(e\cos(1),e\sin(1),e)} \delta\,ds =\int_0^1 \delta(r(t))|\vec v| \\ &=\int_0^1 e^t(\sqrt{3}e^t)\,dt =\left[\dfrac{\sqrt{3}}{2}e^{2t}\right]_0^1 \\ &=\dfrac{\sqrt{3}}{2}(e^2-1) \approx 5.53 \end{aligned}\]
  
  as
2. The \(z\)-component of the center of mass of the wire between \(t=0\) and \(t=1\) with linear density \(\delta=z\).
  
  \(\bar{z}=\dfrac{M_{1z}}{M}\)
  \(\displaystyle M_{1z}=\int_a^b z(t)\delta(r(t))|\vec v|\,dt\)
  
  \(\bar{z}=\dfrac{2(e^2+e+1)}{3(e+1)}\approx1.99\)
  
  From part (a), \(z(t)=e^t\), \(\delta(r(t))=e^t\) and \(|\vec v|=\sqrt{3}e^t\). So the \(z\)-\(1^\text{st}\) moment is: \[\begin{aligned} M_{1z}&=\int_a^b z(t)\delta(r(t))|\vec v|\,dt =\int_0^1 e^t\cdot e^t\cdot\sqrt{3}e^t\,dt\\ &=\int_0^1 \sqrt{3}e^{3t}\,dt =\left[\dfrac{\sqrt{3}}{3}e^{3t}\right]_0^1\\ &=\dfrac{\sqrt{3}}{3}(e^3-1)\\ \end{aligned}\] From part (a), the total mass of the wire is \(M=\dfrac{\sqrt{3}}{2}(e^2-1)\), so the center of mass is: \[ \bar{z} =\dfrac{\dfrac{\sqrt{3}}{3}(e^3-1)}{\dfrac{\sqrt{3}}{2}(e^2-1)} =\dfrac{2(e-1)(e^2+e+1)}{3(e-1)(e+1)} =\dfrac{2(e^2+e+1)}{3(e+1)} \approx1.99 \]
  
  as
3. The work to move a bead along the wire from \(t=0\) to \(t=1\) if the force is \(\vec F=(-y,x,0)\).
  
  \(\displaystyle W=\int_A^B \vec F\cdot d\vec s\)
  
  \(W=\dfrac{1}{2}(e^2-1)\approx 3.19\)
  
  From part (a), \[ \vec v(t)=(e^t\cos(t)-e^t\sin(t),e^t\sin(t)+e^t\cos(t),e^t) \] The force along the curve is \[\begin{aligned} \vec F(\vec r(t))=(-e^t\sin(t),e^t\cos(t),0)\\ \end{aligned}\] So the work is: \[\begin{aligned} W&=\int_{(\cos(0),\sin(0),1)}^{(e\cos(1),e\sin(1),e)} \vec F\cdot d\vec s =\int_0^1 \vec F(r(t))\cdot\vec v(t)\,dt\\ &=\int_0^1 e^{2t}\sin^2(t)+e^{2t}\cos^2(t)\,dt =\int_0^1 e^{2t}\,dt \\ &=\left[\dfrac{1}{2}e^{2t}\right]_0^1 =\dfrac{1}{2}(e^2-1) \approx 3.19 \end{aligned}\]
  
  as
Consider a wire in the shape of the curve \(\vec r(t)=(3t^2,4t^3,3t^4)\). Compute each of the following. Simplify where possible.
1. The mass of the wire between \(t=1\) and \(t=2\) with linear density \(\delta=x\).
  
  \(M=\dfrac{891}{2}=445.5\)
  
  The density on the curve is \(\delta(r(t))=3t^2\). The velocity is: \[\begin{aligned} \vec v&=(6t,12t^2,12t^3) \end{aligned}\] The speed is: \[\begin{aligned} |\vec v(t)| &=\sqrt{(6t)^2+(12t^2)^2+(12t^3)^2}\\ &=\sqrt{36t^2+144t^4+144t^6}\\ &=6t\sqrt{1+4t^2+4t^4}=6t(1+2t^2)\\ \end{aligned}\] So the mass is: \[\begin{aligned} M&=\int_{(3,4,3)}^{(12,32,48)} \delta\,ds =\int_1^2 \delta(r(t))|\vec v|\,dt\\ &=\int_1^2 18t^3(1+2t^2)\,dt =\left[\dfrac{9}{2}t^4+6t^6\right]_1^2\\ &=72+384-\dfrac{9}{2}-6 =\dfrac{891}{2}=445.5 \end{aligned}\]
  
  as
2. The center of mass of the wire between \(t=1\) and \(t=2\) with linear density \(\delta=x\).
  
  \((\bar{x},\bar{y},\bar{z})\approx(9,21.28,28.66)\)
  
  From part (a), \(\delta(r(t))=3t^2\), and \(|\vec v|=6t(1+2t^2)\).
  So the \(x\)-\(1^\text{st}\) moment is: \[\begin{aligned} M_{1x}&=\int_a^b x(t)\delta(r(t))|\vec v|\,dt \\ &=\int_1^2 3t^2\cdot3t^2\cdot6t(1+2t^2)\,dt =\left[9t^6+\dfrac{27}{2}t^8\right]_1^2 \\ &=9(2)^6+\dfrac{27}{2}(2)^8-9-\dfrac{27}{2} =\dfrac{8019}{2}=4009.5\\ \end{aligned}\] The \(y\)-\(1^\text{st}\) moment is: \[\begin{aligned} M_{1y}&=\int_a^b y(t)\delta(r(t))|\vec v|\,dt \\ &=\int_1^2 4t^3\cdot3t^2\cdot6t(1+2t^2)\,dt =\left[\dfrac{72}{7}t^7+16t^9\right]_1^2 \\ &=\dfrac{72}{7}(2)^7+16(2)^9-\dfrac{72}{7}-16 =\dfrac{66376}{7}\approx9482.3\\ \end{aligned}\] The \(z\)-\(1^\text{st}\) moment is: \[\begin{aligned} M_{1z}&=\int_a^b z(t)\delta(r(t))|\vec v|\,dt \\ &=\int_1^2 3t^4\cdot3t^2\cdot6t(1+2t^2)\,dt =\left[\dfrac{27}{4}t^8+\dfrac{54}{5}t^{10}\right]_1^2\\ &=\dfrac{27}{4}(2)^8+\dfrac{54}{5}(2)^{10}-\dfrac{27}{4}-\dfrac{54}{5} =\dfrac{255\,393}{20} \approx12\,769.7\\ \end{aligned}\] From part(a), the total mass of the wire is \(M=445.5\), so the center of mass is: \[ (\bar{x},\bar{y},\bar{z}) \approx\left(\dfrac{4009.5}{445.5},\dfrac{9482.3}{445.5}, \dfrac{12769.7}{445.5}\right) =(9,21.28,28.66) \]
  
  as
3. The work to move a bead along the wire from \(t=1\) to \(t=2\) if the force is \(\vec F=(0,y,x)\).
  
  \(W=882\)
  
  From part (a), \[\begin{aligned} \vec v(t)=(6t,12t^2,12t^3) \end{aligned}\] The force along the curve is \[\begin{aligned} \vec F(\vec r(t))=(0,4t^3,3t^2) \end{aligned}\] So the work is: \[\begin{aligned} W&=\int_{(3,4,3)}^{(12,32,48)} \vec F\cdot d\vec s =\int_1^2 \vec F(r(t))\cdot\vec v(t)\,dt\\ &=\int_1^2 12t^2\cdot4t^3+12t^3\cdot3t^2\,dt\\ &\quad=\int_1^2 84t^5\,dt =\left[14t^6\right]_1^2 =882 \end{aligned}\]
  
  as
Consider a wire in the shape of the curve \(\vec r(t)=(e^t,\sqrt{2}t,e^{-t})\). Compute each of the following. Simplify where possible.
1. The mass of the wire between \(t=0\) and \(t=1\) with linear density \(\delta=x\).
  
  When you compute the speed, the quantity inside the square root is a perfect square.
  
  \(M=\dfrac{1}{2}(e^2+1)\approx 4.19\)
  
  The density on the curve is \(\delta(r(t))=e^t\). The velocity is: \[\begin{aligned} \vec v&=(e^t,\sqrt{2},-e^{-t})\\ \end{aligned}\] The speed is (The quantity inside the square root is a perfect square since \(e^te^{-t}=1\).): \[\begin{aligned} |\vec v(t)| &=\sqrt{e^{2t}+2+e^{-2t}}=e^t+e^{-t}\\ \end{aligned}\] So the mass is: \[\begin{aligned} M&=\int_{(1,0,1)}^{(e,\sqrt{2},e^{-1})} \delta\,ds =\int_0^1 \delta(r(t))|\vec v|\,dt\\ &=\int_0^1 e^t(e^t+e^{-t})\,dt =\left[\dfrac{1}{2}e^{2t}+t\right]_0^1\\ &=\dfrac{1}{2}e^2+1-\,\dfrac{1}{2}e^0 =\dfrac{1}{2}(e^2+1) \approx 4.19 \end{aligned}\]
  
  as
2. The center of mass of the wire between \(t=0\) and \(t=1\) with linear density \(\delta=x\).
  
  \(\begin{aligned} (\bar{x},\bar{y},\bar{z}) &=\left(\dfrac{2e^3+6e-8}{3(e^2+1)}, \dfrac{\sqrt{2}}{2}, \dfrac{2(e-e^{-1})}{e^2+1}\right)\\ &\approx(1.93,0.707,0.560) \end{aligned}\)
  
  From part (a), \(\delta(\vec r(t))=e^t\), and \(|\vec v|=e^t+e^{-t}\).
  So the \(x\)-\(1^\text{st}\) moment is: \[\begin{aligned} M_{1x}&=\int_a^b x(t)\delta(r(t))|\vec v|\,dt =\int_0^1 e^t\cdot e^t\cdot(e^t+e^{-t})\,dt\\ &=\int_0^1 (e^{3t}+e^t)\,dt =\left[\dfrac{1}{3}e^{3t}+e^t\right]_0^1\\ &=\dfrac{1}{3}e^3+e-\dfrac{1}{3}e^0-e^0 =\dfrac{1}{3}e^3+e-\dfrac{4}{3}\\ \end{aligned}\] The \(y\)-\(1^\text{st}\) moment is (using integration by parts): \[\begin{aligned} M_{1y}&=\int_a^b y(t)\delta(r(t))|\vec v|\,dt =\int_0^1 \sqrt{2}t\cdot e^t\cdot(e^t+e^{-t})\,dt\\ &=\sqrt{2}\int_0^1 (te^{2t}+t)\,dt =\sqrt{2}\left[\dfrac{t}{2}e^{2t}-\dfrac{1}{4}e^{2t}+\dfrac{1}{2}t^2\right]_0^1\\ &=\sqrt{2}\left(\dfrac{1}{2}e^2-\dfrac{1}{4}e^2+\dfrac{1}{2}-\dfrac{1}{4}\right) =\dfrac{\sqrt{2}}{4}(e^2+1)\\ \end{aligned}\] The \(z\)-\(1^\text{st}\) moment is: \[\begin{aligned} M_{1z}&=\int_a^b z(t)\delta(r(t))|\vec v|\,dt =\int_0^1 e^{-t}\cdot e^t\cdot(e^t+e^{-t})\,dt \\ &=\int_0^1 (e^t+e^{-t})\,dt =\left[\rule{0pt}{10pt}e^t-e^{-t}\right]_0^1 =e-e^{-1} \end{aligned}\] From part (a), the total mass is \(M=\dfrac{1}{2}(e^2+1)\). So the center of mass is: \[\begin{aligned} (\bar{x},\bar{y},\bar{z}) &=\left(\dfrac{M_{1x}}{M},\dfrac{M_{1y}}{M},\dfrac{M_{1z}}{M}\right) \\ &=\left(\dfrac{\dfrac{1}{3}e^3+e-\dfrac{4}{3}}{\dfrac{1}{2}(e^2+1)}, \dfrac{\dfrac{\sqrt{2}}{4}(e^2+1)}{\dfrac{1}{2}(e^2+1)}, \dfrac{e-e^{-1}}{\dfrac{1}{2}(e^2+1)}\right) \\ &=\left(\dfrac{2e^3+6e-8}{3(e^2+1)}, \dfrac{\sqrt{2}}{2}, \dfrac{2(e-e^{-1})}{e^2+1}\right) \\ &\approx (1.93,0.707,0.560) \end{aligned}\]
  
  as
3. The work to move a bead along the wire from \(t=0\) to \(t=1\) if the force is \(\vec F=(z,0,-x)\).
  
  \(\displaystyle W=\int \vec F\cdot d\vec s=2\)
  
  From part (a), \[ \vec v(t)=(e^t,\sqrt{2},-e^{-t}) \] The force along the curve is \[ \vec F(\vec r(t))=(e^{-t},0,-e^t) \] So the work is: \[\begin{aligned} W&=\int_{(1,0,1)}^{(e,\sqrt{2},e^{-1})} \vec F\cdot d\vec s =\int_0^1 \vec F(r(t))\cdot\vec v(t)\,dt\\ &\quad=\int_0^1 2\,dt=2 \end{aligned}\]
  
  as
Consider a wire in the shape of the curve \(\vec r(t)=(t^2,2t,\ln t)\). Compute each of the following. Simplify where possible.
1. The mass of the wire between \(t=1\) and \(t=2\) with linear density \(\delta=x\).
  
  When you compute the speed, put the quantity inside the square root over a common denominator. Then it will be a perfect square.
  
  \(M=9\)
  
  The density on the curve is \(\delta(r(t))=t^2\). The velocity is: \[\begin{aligned} \vec v&=\left(2t,2,\dfrac{1}{t}\right)\\ \end{aligned}\] The speed is (Put the terms over a common denominator.): \[\begin{aligned} |\vec v(t)| &=\sqrt{4t^2+4+\dfrac{1}{t^2}} =\dfrac{1}{t}(2t^2+1)\\ \end{aligned}\] So the mass is: \[\begin{aligned} M&=\int_{(1,2,0)}^{(4,4,\ln2)} \delta\,ds =\int_1^2 \delta(r(t))|\vec v|\,dt\\ &=\int_1^2 t(2t^2+1)\,dt =\left[\dfrac{1}{2}t^4+\dfrac{1}{2}t^2\right]_1^2\\ &=\dfrac{1}{2}(2^4+2^2)-1=9 \end{aligned}\]
  
  as
2. The center of mass of the wire between \(t=1\) and \(t=2\) with linear density \(\delta=x\).
  
  \((\bar{x},\bar{y},\bar{z}) \approx(2.75,3.27,0.48)\)
  
  From part (a), \(\delta(\vec r(t))=t^2\) and \(|\vec v|=\dfrac{1}{t}(2t^2+1)\).
  So the \(x\)-\(1^\text{st}\) moment is: \[\begin{aligned} M_{1x}&=\int_a^b x(t)\delta(r(t))|\vec v|\,dt =\int_1^2 t^2\cdot t^2\cdot\dfrac{1}{t}(2t^2+1)\,dt\\ &=\int_1^2 t^3(2t^2+1)\,dt =\left[\dfrac{1}{3}t^6+\dfrac{1}{4}t^4\right]_1^2\\ &=\dfrac{1}{3}(2)^6+\dfrac{1}{4}(2)^4-\,\dfrac{1}{3}-\,\dfrac{1}{4} =\dfrac{99}{4}=24.75\\ \end{aligned}\] The \(y\)-\(1^\text{st}\) moment is: \[\begin{aligned} M_{1y}&=\int_a^b y(t)\delta(r(t))|\vec v|\,dt =\int_1^2 2t\cdot t^2\cdot\dfrac{1}{t}(2t^2+1)\,dt\\ &=\int_1^2 2t^2(2t^2+1)\,dt =\left[\dfrac{4}{5}t^5+\dfrac{2}{3}t^3\right]_1^2\\ &=\dfrac{4}{5}(2)^5+\dfrac{2}{3}(2)^3-\,\dfrac{4}{5}-\,\dfrac{2}{3} =\dfrac{442}{15}\approx29.47 \end{aligned}\] The \(z\)-\(1^\text{st}\) moment is (using integration by parts with \(u=\ln t\)): \[\begin{aligned} M_{1z}&=\int_a^b z(t)\delta(r(t))|\vec v|\,dt =\int_1^2 \ln t\cdot t^2\cdot\dfrac{1}{t}(2t^2+1)\,dt\\ &=\int_1^2 \ln t(2t^3+t)\,dt =\left[\dfrac{t^2}{8}(4t^2\ln t+4\ln t-t^2-2)\right]_1^2\\ &=\dfrac{2^2}{8}\left[4(2)^2\ln2+4\ln2-2^2-2\right]+\dfrac{3}{8} \\ &=10\ln2-\dfrac{21}{8}\approx4.31 \end{aligned}\] From part (a), the total mass of the wire is \(M=9\). So the center of mass is: \[\begin{aligned} (\bar{x},\bar{y},\bar{z}) &=\left(\dfrac{M_{1x}}{M},\dfrac{M_{1y}}{M},\dfrac{M_{1z}}{M}\right) \\ &=\left(\dfrac{24.75}{9},\dfrac{29.47}{9},\dfrac{4.31}{9}\right) \approx(2.75,3.27,0.48) \end{aligned}\]
  
  as
3. The work to move a bead along the wire from \(t=1\) to \(t=2\) if the force is \(\vec F=(y,-x,0)\).
  
  \(W=\dfrac{14}{3}\)
  
  From part (a), \[\begin{aligned} \vec v(t)&=\left(2t,2,\dfrac{1}{t}\right) \end{aligned}\] The force along the curve is \[\begin{aligned} \vec F(\vec r(t))&=(2t,-t^2,0) \end{aligned}\] So the work is: \[\begin{aligned} W&=\int_{(1,2,0)}^{(4,4,\ln2)} \vec F\cdot d\vec s =\int_1^2 \vec F(r(t))\cdot\vec v(t)\,dt\\ &\quad=\int_1^2 2t^2\,dt =\left[\dfrac{2}{3}t^3\right]_1^2 =\dfrac{14}{3} \end{aligned}\]
  
  as
Consider a wire in the shape of the curve \(\vec r(t)=(\sinh t,\cosh t,t)\). Compute each of the following. Simplify where possible.
1. The mass of the wire between \(t=0\) and \(t=1\) with linear density \(\delta=x\).
  
  \(M=\dfrac{\sqrt{2}}{2}\sinh^2(1)\)
  
  The density on the curve is \(\delta(r(t))=\sinh(t)\). Since \(\dfrac{d}{dx}\sinh t=\cosh t\) and \(\dfrac{d}{dx}\cosh t=\sinh t\), the velocity is: \[\begin{aligned} \vec v&=(\cosh(t),\sinh(t),1) \end{aligned}\] Since \(\cosh^2t-\sinh^2t=1\), we have \(1+\sinh^2t=\cosh^2t\). So the speed is: \[\begin{aligned} |\vec v(t)| &=\sqrt{\cosh^2(t)+\sinh^2(t)+1} \\ &=\sqrt{\cosh^2(t)+\cosh^2(t)} =\sqrt{2}\cosh(t)\\ \end{aligned}\] So the mass is: \[\begin{aligned} M&=\int \delta\,ds =\int_0^1 \delta(r(t))|\vec v|\,dt\\ &=\int_0^1 \sinh(t)\sqrt{2}\cosh(t)\,dt =\left[\dfrac{\sqrt{2}}{2}\sinh^2(t)\right]_0^1\\ &=\dfrac{\sqrt{2}}{2}\sinh^2(1) \end{aligned}\]
  
  as
2. The \(x\)-component of the center of mass of the wire between \(t=0\) and \(t=1\) with linear density \(\delta=x\).
  
  \(\bar{x}=\dfrac{2}{3}\sinh(1)\approx0.78\)
  
  From part (a), \(\delta(\vec r(t))=\sinh(t)\) and \(|\vec v|=\sqrt{2}\cosh(t)\). So the \(x\)-\(1^\text{st}\) moment is: \[\begin{aligned} M_{1x}&=\int_a^b x(t)\delta(r(t))|\vec v|\,dt =\int_0^1 \sinh t\cdot\sinh(t)\cdot\sqrt{2}\cosh(t)\,dt\\ &=\left[\dfrac{\sqrt{2}}{3}\sinh^3(t)\right]_0^1=\dfrac{\sqrt{2}}{3}\sinh^3(1) \end{aligned}\] From part (a), the total mass of the wire is \(M=\dfrac{1}{\sqrt{2}}\sinh^2(1)\), so the \(x\)-component of the center of mass is: \[\begin{aligned} \bar{x} &=\dfrac{M_{1x}}{M} =\dfrac{\sqrt{2}}{3}\sinh^3(1)\dfrac{\sqrt{2}}{\sinh^2(1)} \\ &=\dfrac{2}{3}\sinh(1) \approx0.78 \end{aligned}\]
  
  as
3. The work to move a bead along the wire from \(t=0\) to \(t=1\) if the force is \(\vec F=(y,-x,0)\).
  
  \(W=1\)
  
  From part (a), \[\begin{aligned} \vec v(t)&=(\cosh(t),\sinh(t),1)\\ \end{aligned}\] The force along the curve is \[\begin{aligned} \vec F(\vec r(t))&=(\cosh(t),-\sinh(t),0)\\ \end{aligned}\] So the work is: \[\begin{aligned} W&=\int \vec F\cdot d\vec s =\int_0^1 \vec F(r(t))\cdot\vec v(t)\,dt\\ &=\int_0^1 \cosh^2(t)-\sinh^2(t)\,dt =\int_0^1 1\,dt =\left[\rule{0pt}{10pt}t\right]_0^1 =1 \end{aligned}\]
  
  as

4. Line Integrals

Exercises

a. Arc Length

b. Line Integrals of Scalars

c. Applications of Scalar Line Integrals

d. Line Integrals of Vectors

e. Applications of Vector Line Integrals

f. Normal Line Integrals in \(\mathbb{R}^2\) (Optional)

g. Applications of Normal Line Integrals (Optional)

Review Exercises

Heading