9. Line Integrals

e. Applications of Vector Line Integrals

2. Flow and Circulation

Let \(\vec V(x,y,z)\) be the velocity of a fluid at the point \((x,y,z)\). The integral \[ \int_A^B \vec V\cdot d\vec s =\int_a^b \vec V\cdot\hat v\,ds \] is called the flow of the fluid along the curve \(\vec r(t)\) from \(A=\vec r(a)\) to \(B=\vec r(b)\).

def_flow

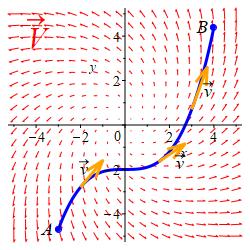
If \(\vec r(t)\) is a closed curve, (i.e. \(A=B\)) then the flow is called the circulation of the fluid. We frequently write \[ \oint_{\vec r} \vec V\cdot d\vec s =\oint_{\vec r} \vec V\cdot\hat v\,ds \] for the circulation to indicate that the curve is closed and we don't need to specify the initial and final points.

def_circ_ccw

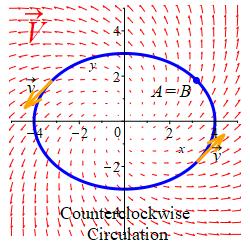
More generally, for any vector field \(\vec F\) the integral \(\displaystyle \int_A^B \vec F\cdot d\vec s\) is called the flow of the vector field along the curve \(\vec r(t)\) from \(A=\vec r(a)\) to \(B=\vec r(b)\), and the integral \(\displaystyle \oint \vec F\cdot d\vec s\) is called the circulation of the vector field around a closed curve.

Caution: Even though you don't need to specify the endpoints for a closed curve, you still need to specify the orientation of the curve, i.e. the direction the curve is traversed. Click here to update the plot for   or   If you reverse the orientation, then the integral will change sign because the sign of the velocity will change. For a parametrized curve, the orientation is usually the direction in which the parameter increases.

Caution: There may be two velocities in many of these problems: The velocity field of the fluid, \(\vec V(x,y,z)\), and the velocity of the curve, \(\vec v(t)\). For this reason, we will refer to the velocity to the curve as the tangent vector.

Find the flow of the fluid velocity field \(\vec V=\langle -yz,xz,2z\rangle\) along the helix \(\vec r(\theta)=(2\cos\theta,2\sin\theta,3\theta)\) from \((2,0,0)\) to \((2,0,6\pi)\).

The tangent vector to the curve is \(\vec v=\langle -2\sin\theta,2\cos\theta,3\rangle\). The fluid velocity field along the curve is \[ \vec V(\vec r(\theta))=(-yz,xz,2z) =(-6\,\theta\sin\theta,6\,\theta\cos\theta,6\,\theta) \] Their dot product is: \[ \vec V\cdot\vec v =12\,\theta\sin^2\theta+12\,\theta\cos^2\theta+18\theta =30\,\theta \] So the flow is \[\begin{aligned} \text{Flow}& =\int_0^{2\pi} \vec V\cdot\vec v\,d\theta =\int_0^{2\pi} 30\,\theta\,d\theta \\ &=\left[15\theta^2\right]_0^{2\pi}=60\pi^2 \end{aligned}\]

The magnetic field produced by the current in a straight wire along the \(z\)-axis is: \[ \vec B=\left\langle \dfrac{-y}{(x^2+y^2)^{3/2}}, \dfrac{x}{(x^2+y^2)^{3/2}},0\right\rangle \] (shown as red arrows). Find the circulation of the magnetic field counterclockwise around the circle \(x^2+y^2=4\) in the \(xy\)-plane (shown in blue). The curve's tangent vectors (shown in orange) point counterclockwise.

Circ-Example-B

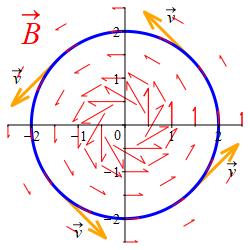
The circle may be parametrized by \(\vec r(\theta)=(2\cos\theta,2\sin\theta,0)\). Notice, this is .

Look at the points \[\begin{aligned} \vec r(0)&=(2,0,0)& \vec r\left(\dfrac{\pi}{2}\right)&=(0,2,0) \\ \vec r(\pi)&=(-2,0,0) & \vec r\left(\dfrac{3\pi}{2}\right)&=(0,-2,0) \\ \end{aligned}\] As \(\theta\) increases, the points move counterclockwise around the circle.

Alternatively, look at the tangent vectors \(\vec v=\langle -2\sin\theta,2\cos\theta,0\rangle\). They point counterclockwise.

Its tangent vector is \(\vec v=\langle -2\sin\theta,2\cos\theta,0\rangle\). The value of the magnetic field on the circle is \[ \vec B=\left\langle \dfrac{-2\sin\theta}{(4)^{3/2}}, \dfrac{2\cos\theta}{(4)^{3/2}},0\right\rangle =\left\langle -\,\dfrac{1}{4}\sin\theta,\dfrac{1}{4}\cos\theta,0\right\rangle \] Their dot product is: \[ \vec B\cdot\vec v =\dfrac{1}{2}\sin^2\theta+\dfrac{1}{2}\cos^2\theta =\dfrac{1}{2} \] So the circulation is \[ \text{Circ} =\int_0^{2\pi} \vec B\cdot\vec v\,d\theta =\int_0^{2\pi} \dfrac{1}{2}\,d\theta=\pi \]

Ampere's Law in Physics says this circulation is equal to \(4\pi\) times the current flowing through the circle. So this magnetic field is produced by a current \(I=\dfrac{1}{4}\). We will learn about this as an application of Stokes' Theorem.

A small ball is pushed by flowing water through a pipe along a path described by the twisted cubic \(\vec r(t)=(t,t^2,t^3)\) from \((0,0,0)\) to \((2,4,8)\). Suppose the fluid velocity of the water is \(\vec V=\left\langle 2z,\dfrac{3}{2}y,kx\right\rangle\) for some number \(k\). If the flow of the water along the path is \(80\), find \(k\).

\(k=5\)

The flow of the water along the twisted cubic \(\vec r(t)=(t,t^2,t^3)\) is given by \[ Flow=\int_A^B \vec V\cdot d\vec s =\int_{(0,0,0)}^{(2,4,8)} \vec V(\vec r(t))\cdot\vec v\,dt \] First, we identify the points \(A=(0,0,0)\) and \(B=(2,4,8)\) as the points where \(t=0\) and \(t=2\), respectively. The fluid velocity, evaluated on the curve, is: \[ \vec V(\vec r(t))=\left\langle 2t^3,\dfrac{3}{2}t^2,kt\right\rangle \] and the tangent vector to the curve is: \[ \vec v=\langle 1,2t,3t^2\rangle \] Their dot product is: \[ \vec V\cdot\vec v=2t^3+3t^3+3kt^3=(5+3k)t^3 \] So the flow is \[\begin{aligned} Flow&=\int_0^2 (5+3k)t^3\,dt =\left[(5+3k)\dfrac{t^4}{4}\right]_0^2 \\ &=4(5+3k) \end{aligned}\] From the problem statement, the flow is \(80\). So \[ 4(5+3k)=80 \quad \Rightarrow \quad 3k=15 \quad \Rightarrow \quad k=5 \]

© MYMathApps

Supported in part by NSF Grant #1123255