9. Line Integrals

g. Applications of Normal Line Integrals (Optional)

1. Expansion and Contraction

Let \(\vec V(x,y)\) be the velocity of a fluid at the point \((x,y)\) and let \(\vec r(t)\) be a closed curve.

Recall, the integral of the tangential component of \(\vec V\) \[ \oint_{\vec r} \vec V\cdot d\vec s =\oint_{\vec r} \vec V\cdot\hat v\,ds \] is the circulation of the fluid around the curve, as previously discussed.

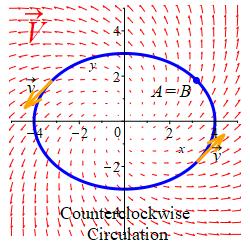
The plot shows a vector field in the x y plane that spirals counterclockwise and increases in magnitude as the distance from the origin increases. In addition, there is an ellipse with tangent vectors that point counterclockwise around the ellipse.

Also recall that if you look in the direction of \(\vec v\), then \(\vec n\) points along your right arm.

Consequently, if the curve is traversed counterclockwise, so that \(\hat n\) points outward, then the integral of the normal component of \(\vec V\) \[ \oint_{\vec r} \vec V\cdot d\vec n =\oint_{\vec r} \vec V\cdot\hat n\,ds \] is called the expansion of the fluid out of the curve \(\vec r(t)\).

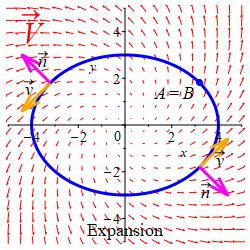
The plot shows a vector field in the x y plane that spirals counterclockwise and increases in magnitude as the distance from the origin increases. In addition, there is the same ellipse with tangent vectors that point counterclockwise around the ellipse and normal vectors that point outward. If you stand on the ellipse facing counterclockwise in the direction of the tangent vectors and put out your right hand, it points in the direction of the outward normal.

On the other hand, if the curve is traversed clockwise, so that \(\hat n\) points inward, then the integral \(\displaystyle \oint_{\vec r} \vec V\cdot d\vec n\) is called the contraction of the fluid into the curve \(\vec r(t)\).

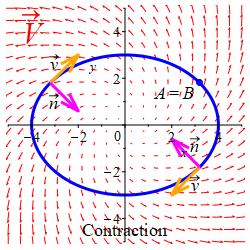
The plot shows the same vector field and ellipse as in the previous plot. however the tangent vectors now point clockwise and the normal vectors now point inward. Again if you stand on the ellipse facing clockwise in the direction of the tangent vectors and put out your right hand, it now points in the direction of the inward normal.

More generally, for any vector field \(\vec F\) the integral \(\displaystyle \oint_{\vec r} \vec F\cdot d\vec n\) is called the expansion (or contraction) of the vector field through the closed curve provided the curve is traversed counterclockwise (or clockwise, resp.).

If the expansion is positive or the contraction is negative, then the fluid is expanding. If the expansion is negative or the contraction is positive, then the fluid is contracting.

Find the expansion of the fluid velocity field \(\vec V=\langle 2x,3y\rangle\) through the circle \(x^2+y^2=16\).

We parametrize the circle by \(\vec r(\theta)=(4\cos\theta,4\sin\theta)\). Then the tangent vector is \(\vec v=\langle -4\sin\theta,4\cos\theta\rangle\) and the normal vector is \(\vec n=\langle 4\cos\theta,4\sin\theta\rangle\). This is outward since it is the same as the radius vector. The fluid velocity field along the curve is \[ \vec V=\langle 8\cos\theta,12\sin\theta\rangle \] Their dot product is \[\begin{aligned} \vec V\cdot\vec n &=32\cos^2\theta+48\sin^2\theta \\ &=16(1+\cos2\theta)+24(1-\cos2\theta) =40-8\cos2\theta \end{aligned}\] So the expansion is \[\begin{aligned} \text{Expansion}&=\int_0^{2\pi} \vec V\cdot\vec n\,d\theta =\int_0^{2\pi} (40-8\cos2\theta)\,d\theta \\ &=\left[40\theta-4\sin2\theta\rule{0pt}{10pt}\right]_0^{2\pi}=80\pi \end{aligned}\]

Find the expansion of the vector field \(\vec G=\langle2x+2y,3x-3y\rangle\) out of the rectangle \(0 \le x \le 3\) and \(0 \le y \le 2\). Integrate over the \(4\) edges and add them up.

The plot shows a rectangle with a normal vector pointing out from each side.

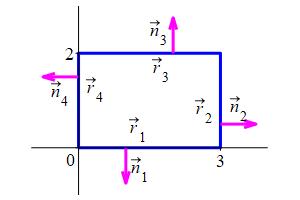
Traverse the rectangle counterclockwise. Parametrize each of the \(4\) edges using \(\vec r(t)=P+t\overrightarrow{PQ}\) where \(P\) and \(Q\) are the starting and finishing points of each edge. The plot shows \(P\) and \(Q\) for the edge \(\vec r_3\).

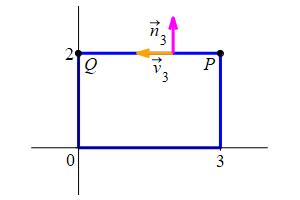
The plot shows a rectangle with a normal vector pointing upward from the top side with a tangent vector pointing left.

\(\text{Expansion}=-6\). Since the expansion is negative, the the vector field \(\vec G\) is contracting.

We parametrize each of the \(4\) edges, counterclockwise, using \(\vec r(t)=P+t\overrightarrow{PQ}\) where \(P\) and \(Q\) are the starting and finishing points of each edge. For each, the parameter range is \(0 \le t \le 1\).
For each of the \(4\) edges, click the Plot button. Here are the endpoints, parametrization, and tangent vector.

\(P=(0,0)\)   \(Q=(3,0)\)   \(\vec r_1=(3t,0)\)     \(\vec v_1=\langle 3,0\rangle\)
\(P=(3,0)\)   \(Q=(3,2)\)   \(\vec r_2=(3,2t)\)     \(\vec v_2=\langle 0,2\rangle\)
\(P=(3,2)\)   \(Q=(0,2)\)   \(\vec r_3=(3-3t,2)\)   \(\vec v_3=\langle -3,0\rangle\)
\(P=(0,2)\)   \(Q=(0,0)\)   \(\vec r_4=(0,2-2t)\)   \(\vec v_4=\langle 0,-2\rangle\)

The plot initially shows the same rectangle as in the problem statement. When the first button is clicked, the only normal is on the bottom edge and there is a tangent vector pointing to the right. When the second button is clicked, the only normal is on the right edge and there is a tangent vector pointing upward. When the third button is clicked, the only normal is on the top edge and there is a tangent vector pointing to the left. When the fourth button is clicked, the only normal is on the left edge and there is a tangent vector pointing downward.

For each of the \(4\) edges, here are the normal vector, the vector field \(\vec G=\langle2x+2y,3x-3y\rangle\) evaluated on the curve, and their dot product. \[\begin{aligned} \vec n_1&=\langle 0,-3\rangle &\vec G_1&=\vec G(3t,0)=\langle 6t,9t\rangle &\vec G_1\cdot\vec n_1&=-27t \\ \vec n_2&=\langle 2,0\rangle &\vec G_2&=\vec G(3,2t)=\langle 6+4t,9-6t\rangle &\vec G_2\cdot\vec n_2&=12+8t \\ \vec n_3&=\langle 0,3\rangle &\vec G_3&=\vec G(3-3t,2)=\langle 10-6t,3-9t)\rangle &\vec G_3\cdot\vec n_3&=9-27t \\ \vec n_4&=\langle -2,0\rangle &\vec G_4&=\vec G(0,2-2t)=\langle 4-4t,-6+6t\rangle &\vec G_4\cdot\vec n_4&=-8+8t \end{aligned}\] For each of the \(4\) edges, here is the normal line integral of \(\vec G\). \[\begin{aligned} \int_{\vec r_1} \vec G\cdot\,d\vec n &=\int_0^1 -27t\,dt=\left[\rule{0pt}{10pt}-\dfrac{27}{2}t^2\right]_0^1=-\dfrac{27}{2} \\ \int_{\vec r_2} \vec G\cdot\,d\vec n &=\int_0^1 12+8t\,dt=\left[\rule{0pt}{10pt}12t+4t^2\right]_0^1=16 \\ \int_{\vec r_3} \vec G\cdot\,d\vec n &=\int_0^1 9-27t\,dt=\left[\rule{0pt}{10pt}9t-\dfrac{27}{2}t^2\right]_0^1=-\,\dfrac{9}{2} \\ \int_{\vec r_4} \vec G\cdot\,d\vec n &=\int_0^1 -8+8t\,dt=\left[\rule{0pt}{10pt}-8t+4t^2\right]_0^1=-4 \end{aligned}\] Finally, we total the \(4\) integrals: \[ \text{Expansion} =\oint \vec G\cdot\,d\vec n =-\dfrac{27}{2}+16+-\,\dfrac{9}{2}-4=-6 \] The fact that the expansion is negative says that the vector field \(\vec G\) is contracting.

In the chapter on Green's Theorem we will learn a much easier way to compute the integrals in the last two problems.

© MY Math Apps

Supported in part by NSF Grant #1123255

NSF logo